从0开始 莫比乌斯函数和反演 学习笔记
莫比乌斯
0 前言
建议先看这篇比较简略的文章(有大概了解)
莫比乌斯函数_为最后的荣光的博客-CSDN博客
再根据个人情况食用本篇博客
1 莫比乌斯函数
1 1 定义
首先对 n n n 唯一分解:
唯一分解:
唯一分解定理一篇就够了_求唯一分解式程序_JdiLfc的博客-CSDN博客
唯一分解定理及其证明 - 夶 - 博客园 (cnblogs.com)
n = p 1 k 1 p 2 k 2 … p m k m , 其中 p i 为 n 的互异质因子 , ∀ i , k i 为正整数 (0) n=p_1^{k_1}p_2^{k_2}\dots p_m^{k_m},其中p_i为n的互异质因子,\forall i,k_i为正整数 \tag{0} n=p1k1p2k2…pmkm,其中pi为n的互异质因子,∀i,ki为正整数(0)
μ ( n ) = { 1 , n = 1 0 , ∃ i , k i ≠ 1 ( − 1 ) m , ∀ i , k i = 1 (1) \mu(n)= \begin{cases} 1,\quad n=1\\ 0, \quad \exist i,k_i\neq1\\ (-1)^m,\quad \forall i, k_i=1 \end{cases} \tag{1} μ(n)=⎩ ⎨ ⎧1,n=10,∃i,ki=1(−1)m,∀i,ki=1(1)
1 2 性质
1 2 1 性质一
莫比乌斯函数是积性函数
积性函数:
(在这里只需要知道定义基本上就🆗了)
[积性函数的性质及证明 + 线性筛_新熊君的博客-CSDN博客](https://blog.csdn.net/wubaizhe/article/details/76711158#:~:text=定义: 对于一个定义域为 N %2B 的函数 f ,对于任意两个互质的正整数 a%2Cb,(ab) %3D f (a)f (b) ,则函数 f 被称为完全积性函数。)
积性函数 - Wuweizheng - 博客园 (cnblogs.com)
积性函数与线性筛 - 租酥雨 - 博客园 (cnblogs.com)
即 μ ( n m ) = μ ( n ) μ ( m ) \mu(nm)=\mu(n)\mu(m) μ(nm)=μ(n)μ(m)
这个证明过于显然了点
m = 1 m=1 m=1,所以 μ ( m n ) = μ ( 1 ) μ ( n ) = μ ( n ) \mu(mn)=\mu(1)\mu(n)=\mu(n) μ(mn)=μ(1)μ(n)=μ(n)
因为 μ ( m ) = μ ( 1 ) = 1 \mu(m)=\mu(1)=1 μ(m)=μ(1)=1, μ ( m ) μ ( n ) = μ ( m n ) \mu(m)\mu(n)=\mu(mn) μ(m)μ(n)=μ(mn)成立
当 g c d ( n , m ) = 1 gcd(n,m)=1 gcd(n,m)=1时,显然 m , n m,n m,n 各自互异质因子的并集= m n mn mn 的互异质因子
并且无交集(因为 m , n m,n m,n互质)
所以 m m m 互异质因子个数+ n n n 互异质因子个数 = m n mn mn 的互异质因子个数
μ ( m ) μ ( n ) = ( − 1 ) s m ( − 1 ) s n = ( − 1 ) s m + s n = μ ( m n ) \mu(m)\mu(n)=(-1)^{s_m}(-1)^{s_n}=(-1)^{s_m+s_n}=\mu(mn) μ(m)μ(n)=(−1)sm(−1)sn=(−1)sm+sn=μ(mn)成立
其中 s n s_n sn 表示 n n n 互异质因子的个数
1 2 2 性质二
对于任意正整数 n n n ,有:
∑ d ∣ n μ ( d ) = { 1 , n = 1 0 , n ≠ 1 (2) \sum_{d|n}\mu(d)= \begin{cases} 1,\quad n=1\\ 0, \quad n\neq1 \end{cases} \tag{2} d∣n∑μ(d)={1,n=10,n=1(2)
证明:
n = 1 n=1 n=1 时, ∑ d ∣ n μ ( d ) = μ ( 1 ) = 1 \sum_{d|n}\mu(d)=\mu(1)=1 ∑d∣nμ(d)=μ(1)=1
n ≠ 1 n\neq1 n=1 时, ∑ d ∣ n μ ( d ) = ∑ i = 0 m C m i ( − 1 ) i = 0 \sum_{d|n}\mu(d)=\sum_{i=0}^m C_m^i(-1)^i=0 ∑d∣nμ(d)=∑i=0mCmi(−1)i=0
为什么呢?
首先对 n n n
唯一分解(查看 ( 0 ) (0) (0))设 d = p 1 q 1 p 2 q 2 … p m q m d=p_1^{q_1}p_2^{q_2}\dots p_m^{q_m} d=p1q1p2q2…pmqm,其中 ∀ 1 ≤ i ≤ m , 0 ≤ q i ≤ k i \forall 1\leq i\leq m, 0\leq q_i\leq k_i ∀1≤i≤m,0≤qi≤ki
当 ∃ i , q i ≥ 2 \exist i,q_i \geq 2 ∃i,qi≥2 时, μ ( d ) = 0 \mu(d)=0 μ(d)=0
因此我们只需要考虑只存在 q i = 1 o r 0 q_i=1\space or \space 0 qi=1 or 0 的情况
设 s = ∑ i = 1 m [ q i ≠ 0 ] s=\sum_{i=1}^m[q_i\neq0] s=∑i=1m[qi=0]
那么 μ ( d ) = ( − 1 ) s \mu(d)=(-1)^s μ(d)=(−1)s
这样的 d d d 显然只有 C m s C_m^s Cms 个
解释:
因为当 d d d 有 s s s 个互异质因子的时候
这 s s s 个质因子显然是 n n n 的 m m m 个互异质因子之中
因此 d d d 就是从 m m m 个数中选 s s s 个数(有区别)的方案数
即组合数 C m s C_{m}^s Cms
虽然是从0开始,但不至于连组合数是什么都不知道吧因此,现在我们可以得出:
∑ d ∣ n μ ( d ) = ∑ s = 0 m C m s ( − 1 ) s \sum_{d|n}\mu(d)=\sum_{s=0}^{m}C_m^s(-1)^s ∑d∣nμ(d)=∑s=0mCms(−1)s
根据
二项式定理, ∑ d ∣ n μ ( d ) = ∑ s = 0 m C m s ( − 1 ) s = 0 \sum_{d|n}\mu(d)=\sum_{s=0}^{m}C_m^s(-1)^s=0 ∑d∣nμ(d)=∑s=0mCms(−1)s=0二项式定理:
【高中数学基础课】二项式定理 - 知乎 (zhihu.com)
emmm还是只看公式就基本上🆗了
反正我们是信息竞赛又不是数学竞赛不过要是有dalao能把证明看懂的话就orz
(但是这好像是高中数学的知识,初三狗表示我不会)
1 3 求解
由于 μ ( n ) \mu(n) μ(n) 是积性函数,所以可以用线性筛法在 O ( n ) O(n) O(n)内完成
不知道的看
积性函数
void get_mu(ll n){mu[1]=1;// 存放 莫比乌斯函数;//isp[] 存放 是否是质数//pri[] 存放 质数 for(int i=2;i<=n;i++){if(!isp[i]) {pri[++cnt]=i;mu[i]=-1;}for(int j=1;j<=cnt&&i*pri[j]<=n;j++){isp[i*pri[j]]=1;if(i%pri[j]==0){mu[i*pri[j]]=0;break;}//也可以直接break 因为里面本来存的就是0 else mu[i*pri[j]]=-mu[i]; } }
}
1 4 *超级实用的“公式”
[ g c d ( i , j ) = 1 ] = ∑ d ∣ g c d ( i , j ) μ ( d ) [gcd(i,j)=1]=\sum_{d|gcd(i,j)}\mu(d) [gcd(i,j)=1]=d∣gcd(i,j)∑μ(d)
证明:
根据性质二 ∑ d ∣ n μ ( d ) = [ n = 1 ] \sum_{d|n}\mu(d)=[n=1] ∑d∣nμ(d)=[n=1]
将 g c d ( i , j ) gcd(i,j) gcd(i,j)带入上式 n n n
得到 ∑ d ∣ g c d ( i , j ) μ ( d ) = [ g c d ( i , j ) = 1 ] \sum_{d|gcd(i,j)}\mu(d)=[gcd(i,j)=1] ∑d∣gcd(i,j)μ(d)=[gcd(i,j)=1]
2 莫比乌斯反演
2 1 公式
f ( n ) = ∑ d ∣ n g ( d ) ⇒ g ( n ) = ∑ d ∣ n f ( n d ) μ ( d ) f(n)=\sum_{d|n}g(d)\Rightarrow g(n)=\sum_{d|n}f(\frac{n}{d})\mu(d) f(n)=d∣n∑g(d)⇒g(n)=d∣n∑f(dn)μ(d)
2 2 证明

2 3 变形
2 3 1 形式一(倍数形式)
f ( i ) = ∑ d = 1 ⌊ n i ⌋ g ( d i ) ⇒ g ( i ) = ∑ d = 1 ⌊ n i ⌋ f ( d i ) μ ( d ) f(i)=\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}g(di)\Rightarrow g(i)=\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}f(di)\mu(d) f(i)=d=1∑⌊in⌋g(di)⇒g(i)=d=1∑⌊in⌋f(di)μ(d)
证明:
(和一般形式类似)
将 g ( i ) = ∑ d = 1 ⌊ n i ⌋ f ( d i ) μ ( d ) g(i)=\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}f(di)\mu(d) g(i)=∑d=1⌊in⌋f(di)μ(d) 带入前式
f ( i ) = ∑ d = 1 ⌊ n i ⌋ g ( d i ) f(i)=\sum_{d=1}^{\lfloor\frac{n}{i}\rfloor}g(di) f(i)=d=1∑⌊in⌋g(di)f ( i ) = ∑ d = 1 ⌊ n i ⌋ ∑ d 1 = 1 ⌊ n i ⌋ f ( d d 1 i ) μ ( d 1 ) f(i)=\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}\sum_{d_1=1}^{\lfloor \frac{n}{i} \rfloor}f(dd_1i)\mu(d_1) f(i)=d=1∑⌊in⌋d1=1∑⌊in⌋f(dd1i)μ(d1)
设 T = d d 1 T=dd1 T=dd1,则:
f ( i ) = ∑ T = 1 ⌊ n i ⌋ ∑ d = 1 ⌊ n i ⌋ f ( T i ) μ ( T d ) f(i)=\sum_{T=1}^{\lfloor \frac{n}{i} \rfloor}\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}f(Ti)\mu(\frac{T}{d}) f(i)=T=1∑⌊in⌋d=1∑⌊in⌋f(Ti)μ(dT)f ( i ) = ∑ T = 1 ⌊ n i ⌋ f ( T i ) [ ∑ d = 1 ⌊ n i ⌋ μ ( T d ) ] f(i)=\sum_{T=1}^{\lfloor \frac{n}{i} \rfloor}f(Ti)[\sum_{d=1}^{\lfloor \frac{n}{i} \rfloor}\mu(\frac{T}{d})] f(i)=T=1∑⌊in⌋f(Ti)[d=1∑⌊in⌋μ(dT)]
f ( i ) = ∑ T = 1 ⌊ n i ⌋ f ( T i ) [ ∑ d 1 ∣ T μ ( d 1 ) ] f(i)=\sum_{T=1}^{\lfloor \frac{n}{i} \rfloor}f(Ti)[\sum_{d_1|T}\mu(d_1)] f(i)=T=1∑⌊in⌋f(Ti)[d1∣T∑μ(d1)]
根据莫比乌斯函数的性质二
∑ d ∣ n μ ( d ) = { 1 , n = 1 0 , n ≠ 1 \sum_{d|n}\mu(d)= \begin{cases} 1,\quad n=1\\ 0, \quad n\neq1 \end{cases} d∣n∑μ(d)={1,n=10,n=1
当 T = 1 T=1 T=1时, ∑ d 1 ∣ T μ ( d 1 ) = 1 \sum_{d_1|T}\mu(d_1)=1 ∑d1∣Tμ(d1)=1, f ( i ) [ ∑ d 1 ∣ T μ ( d 1 ) ] = f ( i ) μ ( 1 ) = f ( i ) f(i)[\sum_{d_1|T}\mu(d_1)]=f(i)\mu(1)=f(i) f(i)[∑d1∣Tμ(d1)]=f(i)μ(1)=f(i)当 T ≠ 1 T\neq1 T=1时, ∑ d 1 ∣ T μ ( d 1 ) = 0 \sum_{d_1|T}\mu(d_1)=0 ∑d1∣Tμ(d1)=0, f ( T i ) [ ∑ d 1 ∣ T μ ( d 1 ) ] = 0 f(Ti)[\sum_{d_1|T}\mu(d_1)]=0 f(Ti)[∑d1∣Tμ(d1)]=0
综上,
f ( i ) = ∑ T = 1 ⌊ n i ⌋ f ( T i ) [ ∑ d 1 ∣ T μ ( d 1 ) ] = f ( i ) f(i)=\sum_{T=1}^{\lfloor \frac{n}{i} \rfloor}f(Ti)[\sum_{d_1|T}\mu(d_1)]=f(i) f(i)=T=1∑⌊in⌋f(Ti)[d1∣T∑μ(d1)]=f(i)
2 3 2 形式二(整除形式)
f ( i ) = ∑ d ∣ i g ( d ) ⇒ g ( i ) = ∑ d ∣ i f ( i d ) μ ( d ) f(i)=\sum_{d|i}g(d)\Rightarrow g(i)=\sum_{d|i}f(\frac{i}{d})\mu(d) f(i)=d∣i∑g(d)⇒g(i)=d∣i∑f(di)μ(d)
就是一般形式
2 4 性质
f ( n ) 是积性函数 ⇔ g ( n ) 是积性函数 f(n)是积性函数\Leftrightarrow g(n)是积性函数 f(n)是积性函数⇔g(n)是积性函数
3 应用
3 1 [HAOI2011]Problem b
3 1 1 题目大意
求当 i ∈ [ a , b ] , j ∈ [ c , d ] i∈[a,b],j∈[c,d] i∈[a,b],j∈[c,d],满足 g c d ( i , j ) = k gcd(i,j)=k gcd(i,j)=k的数对 ( i , j ) (i,j) (i,j)的个数
即
a n s = ∑ i = a b ∑ j = c d [ g c d ( i , j ) = k ] ans=\sum_{i=a}^{b}\sum_{j=c}^{d}[gcd(i,j)=k] ans=i=a∑bj=c∑d[gcd(i,j)=k]
3 1 2 SOLUTION
定义函数 f f f
f ( n , m ) = ∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = k ] f(n,m)=\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=k] f(n,m)=∑i=1n∑j=1m[gcd(i,j)=k]
显然 a n s ans ans可以由函数 f f f 容斥得到
a n s = f ( c , d ) − f ( a − 1 , d ) − f ( b , c − 1 ) + f ( a − 1 , c − 1 ) ans=f(c,d)−f(a−1,d)−f(b,c−1)+f(a−1,c−1) ans=f(c,d)−f(a−1,d)−f(b,c−1)+f(a−1,c−1)
现在考虑怎么求 f f f
根据1 1 4*超级实用的公式可得
f ( n , m ) = ∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = k ] f(n,m)=\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=k] f(n,m)=i=1∑nj=1∑m[gcd(i,j)=k]
f ( n , m ) = ∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ m k ⌋ ∑ d ∣ g c d ( i , j ) μ ( d ) f(n,m)=\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}\sum_{d|gcd(i,j)}\mu(d) f(n,m)=i=1∑⌊kn⌋j=1∑⌊km⌋d∣gcd(i,j)∑μ(d)
枚举 d ′ = d g c d d'=\frac{d}{gcd} d′=gcdd
f ( n , m ) = ∑ d = 1 m i n ( ⌊ n k ⌋ , ⌊ m k ⌋ ) μ ( d ) g ( k d ) f(n,m)=\sum_{d=1}^{min(\lfloor\frac{n}{k}\rfloor,\lfloor\frac{m}{k}\rfloor)}\mu(d)g(kd) f(n,m)=d=1∑min(⌊kn⌋,⌊km⌋)μ(d)g(kd)
g ( d ) 表示 i [ 1 , n ] , j [ 1 , m ] 满足 d ∣ g c d ( x , y ) 的对数 g(d)表示i[1,n],j[1,m]满足d|gcd(x,y)的对数 g(d)表示i[1,n],j[1,m]满足d∣gcd(x,y)的对数
显然可以知道 g ( d ) = ⌊ n d ⌋ ⌊ m d ⌋ 显然可以知道g(d)=\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor 显然可以知道g(d)=⌊dn⌋⌊dm⌋
f ( n , m ) = ∑ d = 1 m i n ( ⌊ n k ⌋ , ⌊ m k ⌋ ) μ ( d ) × ⌊ n k d ⌋ × ⌊ m k d ⌋ f(n,m)=\sum_{d=1}^{min(\lfloor\frac{n}{k}\rfloor,\lfloor\frac{m}{k}\rfloor)}\mu(d)\times\lfloor\frac{n}{kd}\rfloor\times\lfloor\frac{m}{kd}\rfloor f(n,m)=d=1∑min(⌊kn⌋,⌊km⌋)μ(d)×⌊kdn⌋×⌊kdm⌋
浅谈莫比乌斯反演 - B1ueC4t 的博客 - 洛谷博客 (luogu.com.cn)
莫比乌斯反演-让我们从基础开始 - An_Account 的博客 - 洛谷博客 (luogu.com.cn)
莫比乌斯反演 - OI Wiki (oi-wiki.org)
莫比乌斯函数及其应用 - ZAP-Queries + Problem b + GCD_莫比乌斯函数应用_njuptACMcxk的博客-CSDN博客
就可以直接计算了
就是这么简单~~(才怪)~~
3 1 3 CODE
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+2;
int T,a,b,c,d,k,mu[N],SumMu[N],pri[N],isp[N],cnt;
int Mobius(int n,int m,int k){//(i[1,n]j[1,m]{[gcd(i,j)=k]})的个数if(n>m) swap(n,m);n/=k,m/=k; int ans=0;for(int i=1,j;i<=n;i=j+1) {j=min(n/(n/i),m/(m/i));ans+=(SumMu[j]-SumMu[i-1])*(n/i)*(m/i);}return ans;
}
void Mu(int n);//见模板部分
int main(){Mu(N-2);ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>T;while(T--){cin>>a>>b>>c>>d>>k;cout<<Mobius(b,d,k)-Mobius(b,c-1,k)-Mobius(a-1,d,k)+Mobius(a-1,c-1,k)<<"\n";}return 0;
}
「BZOJ2693」jzptab
【BZOJ2693】jzptab - yoyoball - 博客园 (cnblogs.com)
搞半天发现这个模数搞错了。。。。尬住了,ԾㅂԾ,
[BZOJ4407]于神之怒加强版 - 租酥雨 - 博客园 (cnblogs.com)
枚举倍数真的是一个非常常见并且常用的套路啊!!
4 后话
整除分块 - pengym - 博客园 (cnblogs.com)
最后,我想说莫比乌斯反演-让我们从基础开始 - An_Account 的博客 - 洛谷博客 (luogu.com.cn)这篇博客非常的实用(just tell you the sercet of the common probelms’ solution),但是如果想彻底了解的话,我们还是老老实实学吧…( _ _)ノ|
完结撒花❀
★,°:.☆( ̄▽ ̄)/$:.°★ 。
相关文章:

从0开始 莫比乌斯函数和反演 学习笔记
莫比乌斯 0 前言 建议先看这篇比较简略的文章(有大概了解) 莫比乌斯函数_为最后的荣光的博客-CSDN博客 再根据个人情况食用本篇博客 1 莫比乌斯函数 1 1 定义 首先对 n n n 唯一分解: 唯一分解: 唯一分解定理一篇就够了_求…...

IntersectionObserver“替代”滚动条监听
概要 IntersectionObserver 接口提供了一种异步观察目标元素与其祖先元素或顶级文档视口(viewport)交叉状态的方法。其祖先元素或视口被称为根(root)。 当一个 IntersectionObserver 对象被创建时,其被配置为监听根中…...
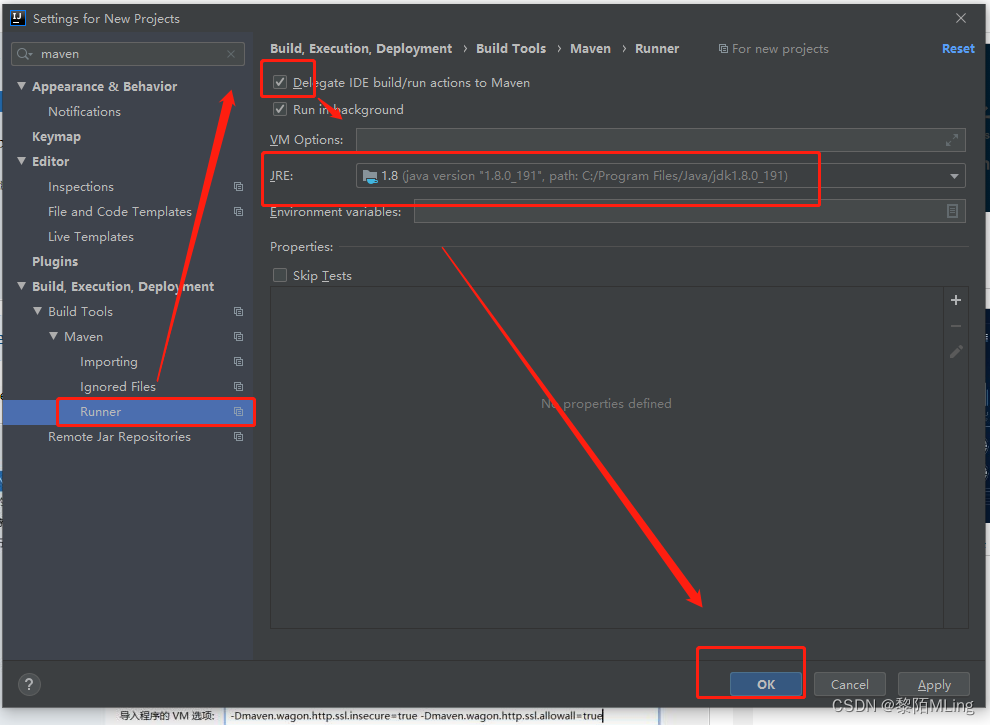
Maven下载安装及IDEA配置Maven的超详细教程
Maven下载安装及IDEA配置Maven的超详细教程 1、IntelliJ IDEA 下载、安装及配置过程2、maven下载、安装、配置过程2.1 mavan下载2.2 安装2.3 配置 3、在IDEA中配置Maven3.1 进入设置界面3.2 maven配置 4、IDEAmaven创建工程示例 Maven是一个能使我们的java程序开发节省时间和精…...
【JAVAEE】线程池基础知识⭐
目录 1.什么是线程池 2.为什么要使用线程池 3.怎么使用线程池 4.自定义一个线程池 5.为什么不推荐使用系统自带的线程池 5.1线程池构造方法的参数和含义 5.1.1拒绝策略 5.2线程池的工作原理 5.3为什么不适用系统自带的线程池 补充:工厂模式 1.什么是线程池…...

【源码解析】@ControllerAdvice实现异常捕获与响应增强处理的原理解析
全局异常处理 demo展示 Slf4j RestControllerAdvice public class GlobalExceptionAdvice {ExceptionHandler(RuntimeException.class)public R<Void> handleNotPermissionException(RuntimeException e, HttpServletRequest request) {String requestURI request.get…...

Visual Studio Code 插件的开发、调试及发布完整详细教程
本篇文章主要讲解:Vscode的拓展插件,从环境安装到生成项目文件再到调试及部署发布的完整开发教程。 日期:2023年5月10日 vscode 1.78.1 一、准备node环境及安装yo 项目初始化,优先安装yo、再通过yo创建code及插件项目。 基础条件 需要先安装node,且node环境已经正确安装…...
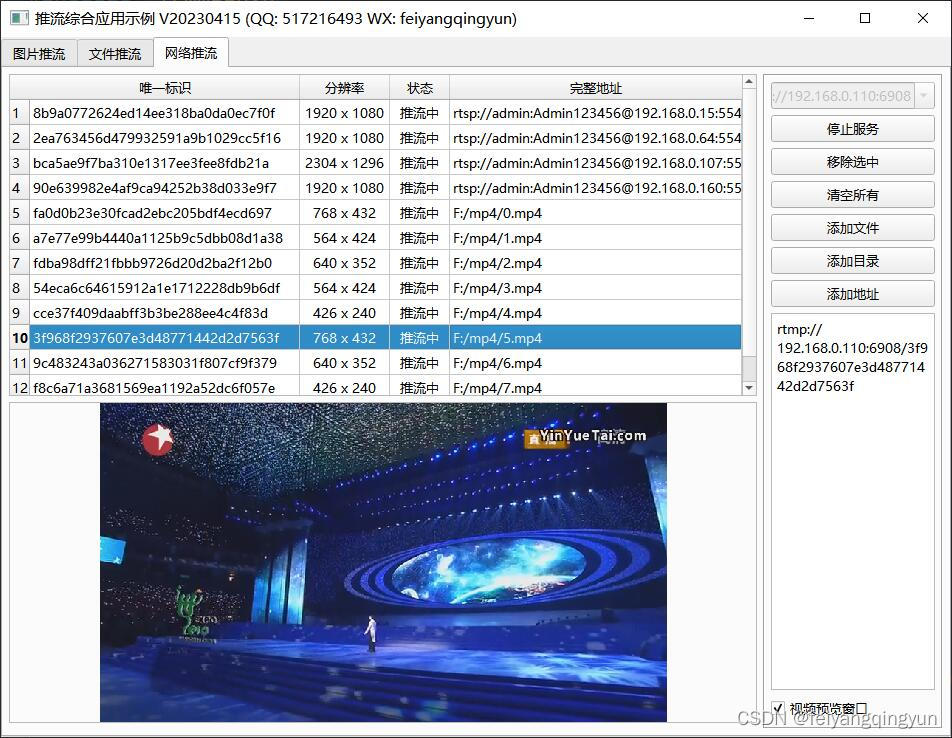
Qt音视频开发38-ffmpeg视频暂停录制的设计
一、前言 基本上各种播放器提供的录制视频接口,都是只有开始录制和结束录制两个,当然一般用的最多的也是这两个接口,但是实际使用过程中,还有一种可能需要中途暂停录制,暂停以后再次继续录制,将中间部分视频不需要录制,跳过这部分不需要的视频,而且录制的视频文件必须…...

bat脚本、dos命令
bat脚本 bat脚本就是DOS批处理脚本,就是将一系列DOS命令按照一定顺序排列而形成的集合,运行在windows命令行环境上。这个文件的每一行都是一条DOS命令 在命令提示下键入批处理文件的名称,或者双击该批处理文件,系统就会调用Cmd.…...

【星戈瑞】Sulfo-Cyanine5 mal红色荧光Cy5-maleimide
Sulfo-Cyanine5 mal是一种具有强荧光信号的染料,主要应用于生物荧光成像领域。它的化学式为C38H43KN4O9S2,分子量为803.00。这种染料具有良好的水溶性,可在水溶液中稳定存在。它的光学特性包括吸收峰位于646 nm和发射峰位于662 nm,…...
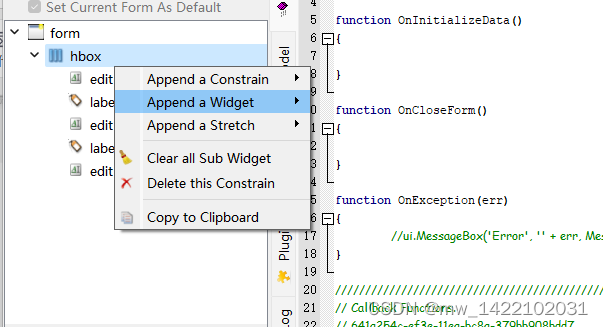
Dcip的学习1-计算器
文章目录 前言一、配置安装环境1.1 网址1.2 再次打开需要进行的操作1.3 NodeJS控制台的操作1.4 出现的页面 二、Dcip生成计算器2.1 软件的基本单位 - Unitform中添加内容 2.2 OnleftChange(); 前言 只是为方便学习,不做其他用途, 一、配置安装环境 1.1 …...

ChatGPT使用9大技巧详解
目录 技巧1:To Do and Not To Do 技巧2:增加示例 技巧3:使用引导词,引导模型输出特定内容...
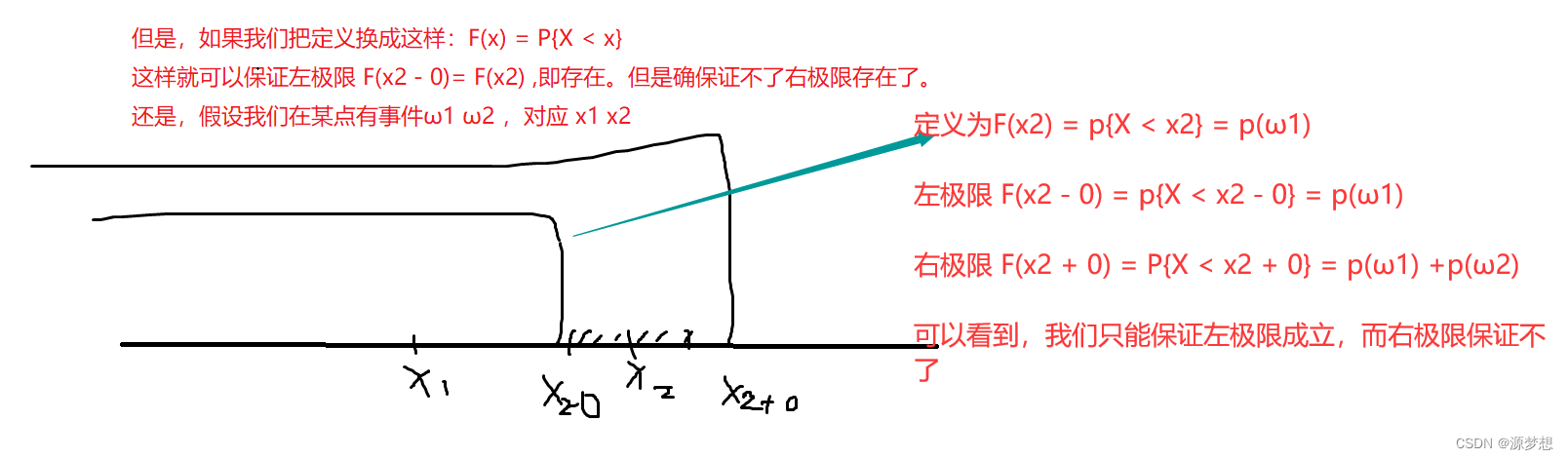
随机变量X,分布函数X~F(x)的理解。
1.随机变量X 1.通常认知的"x"与随机变量X 我们通常意义上的 x 是自变量,y f(x) 中的自变量。 但是 X 更多意义是 对应法则 " f " ,X完整写法是 X(ω) ω ∈ Ω。 X这个对应法则,可以将样本点映射到实数轴上。 那么X这…...

11.构造器的查询.分块.聚合
学习要点: 1.构造器查询 2.分块.聚合 本节课我们来开始学习数据库的构造器查询以及分块和聚合查询。 一.构造器查询 1. table()方法引入相应的表,get()方法可以查询当前表的所有数据; //获取全部结果 $users DB::table(users)-&g…...
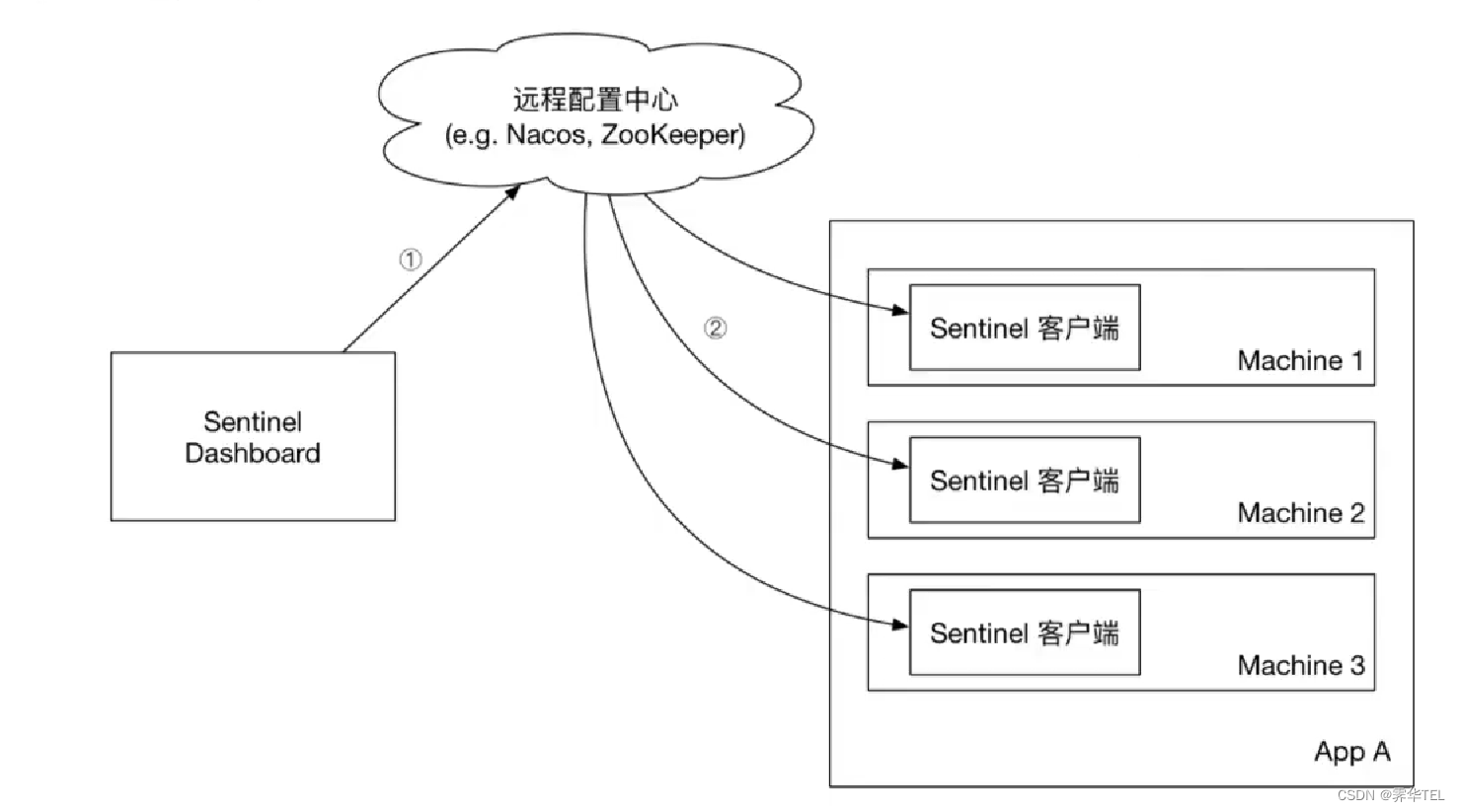
微服务保护——Sentinel
初识Sentinel 雪崩问题 微服务调用链路中的某个服务故障,引起整个链路中的所有微服务都不可用,这就是雪崩。 解决雪崩问题的常见方式有四种: 超时处理:设定超时时间,请求超过一定时间没有响应就返回错误信息,不会无休止等待舱壁…...

MySQL面试整理
https://houchen-study.oss-cn-hangzhou.aliyuncs.com/%E9%9D%A2%E8%AF%95/MySQL/MySQL%E9%9D%A2%E8%AF%95%E5%A4%A7%E5%85%A8%281%29.pdf 数据库基础知识 为什么要使用数据库? 什么是MySQL? 数据库的三大范式是什么? MySQL有关权限的表…...
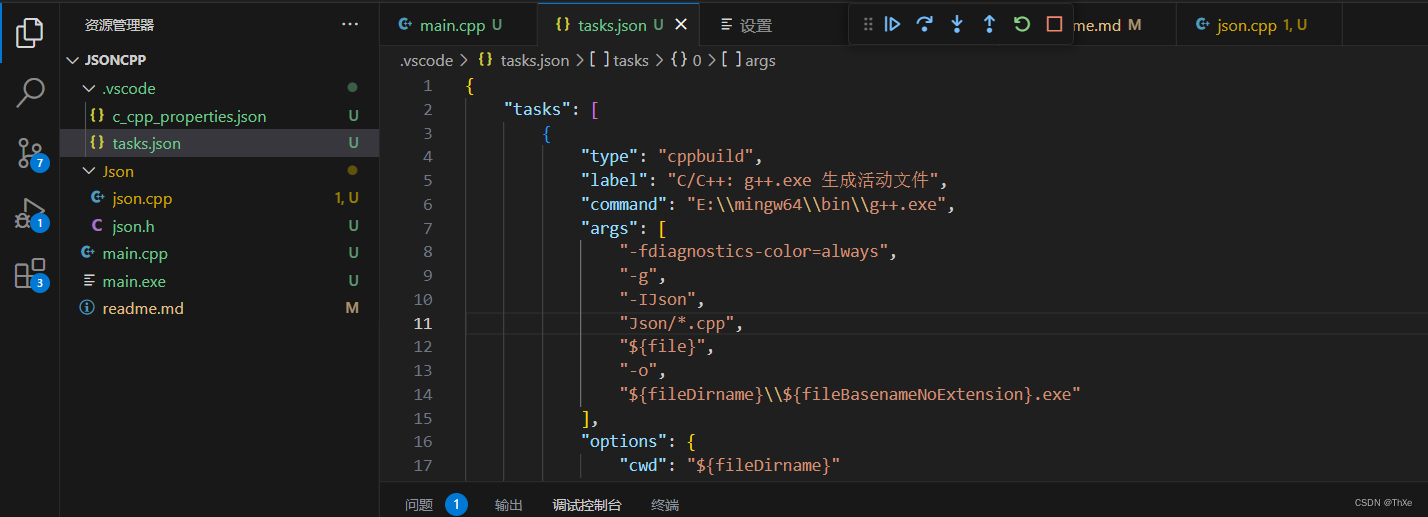
Vscode C++环境配置
多文件编译 打开设置搜索coderunner 找到Executor Map 加入-I目录名 目录名/*.cpp 调试 点击调试以后会产生tasks.json文件,加入链接文件和库文件...

matlab小波去噪
本文将为您介绍如何利用MATLAB进行小波去噪处理,并应用于实际数据。小波去噪是一种通过对数据进行小波分解和重构的方法,有效地去除信号中的噪声,提高信号质量。该方法不仅广泛应用于信号处理、图像处理等领域,在实际生产和科研中…...

为什么要采用全网营销策略?全网营销有何优势?
现在市场上有很多全网营销公司,其实很多企业的经理人疑惑全网营销是要干什么?这些公司能干什么?这里小马识途营销顾问给大家做一个整体的解读。 全网营销,概括地说就是在整个互联网,利用各类互联网平台和工具对产品和服…...
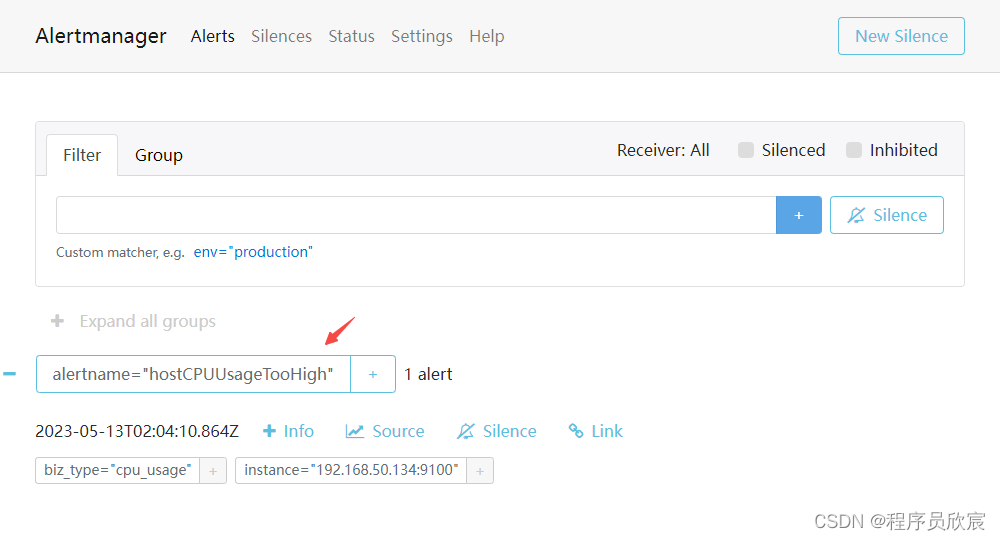
prometheus实战之四:alertmanager的部署和配置
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《prometheus实战》系列的第四篇,在《prometheus实战之三:告警规则》中曾经提到过,整个告警功能分为规则和…...

【Python】glob 包的介绍和使用
glob 是 Python 标准库中的一个模块,它提供了一种查找符合特定模式的路径名的方法,类似于命令行中的 glob 命令。glob 模块用于读取指定路径下的所有符合特定规律的文件名,非常适合用于读取文件夹中的文件列表和操作符合特定规律文件列表。 …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
