【智能计算数学】微积分
高数
- 问题解决流程
- 引例:回归
- 回归
- 引例:分类
- 分类
- 线性可分
- FLD
- 线性不可分
- 智能计算讨论范围
- 下降法
- 为什么要用下降法?- 解析解很难写出公式或很复杂难计算
- 有哪些常用的下降法?- 梯度下降&高斯-牛顿法
- 梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
- 如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
- 结论:下降最快的方向为梯度的反方向,即梯度下降。
- 牛顿法 - 本质:二阶泰勒展开式近似
- 如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
- 分类&回归
- 线性分析
- 常用不等式
- 绝对值不等式
- 柯西不等式
- 算术-几何平均不等式
- 数列极限
- 序列极限
- 上极限
- 下极限
- 级数
- 点集拓扑
- 开集
- 开集性质
- 闭集
- 闭集性质
- 紧集
- Heine-Borel定理
- 例题:判断Rn\mathbb{R^n}Rn和∅\emptyset∅是否开闭紧?
- 函数连续性
- 函数连续定义
- Lipshitz函数是连续函数
- Lipshitz函数与机器学习
- 连续函数逼近
- 拉格朗日插值定理
- 连续函数性质
- 最值定理
- 介值定理
- 不连续函数
- 导数
- 一元函数导数
- 定义
- 意义
- 性质
- 极值定理
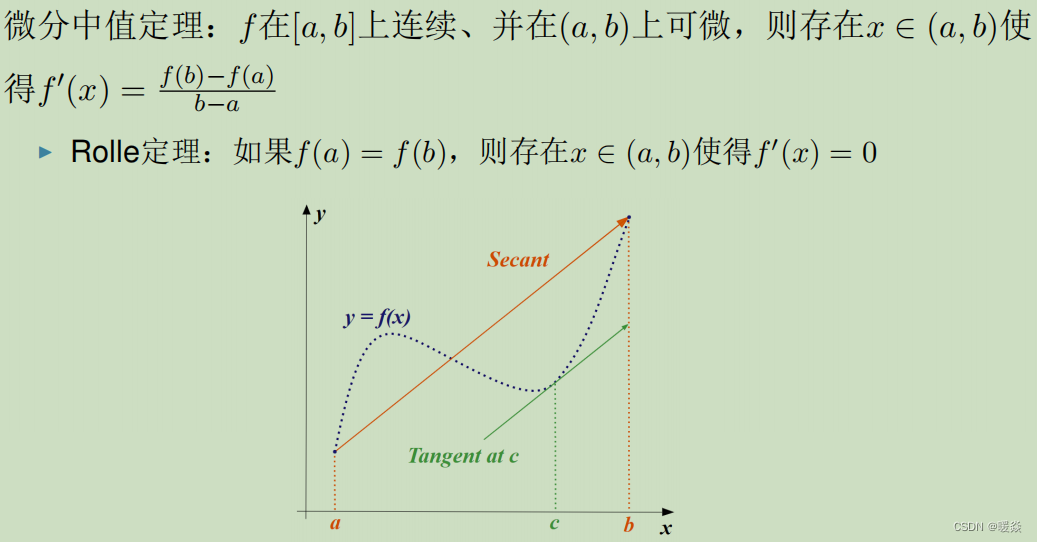
- 微分中值定理
- 洛必达法则
- 常用公式
- C∞C^\inftyC∞
- 多元多值函数
- 可微
- 梯度存在
问题解决流程
idea - math - optimization - algorithm
引例:回归

question:123456x,预测x值为多少?
idea:f(xi)=atxi+b,f(xi)≈yif(x_i)=a^tx_i+b, f(x_i)\approx y_if(xi)=atxi+b,f(xi)≈yi,使用f(x)f(x)f(x)预测新样本xxx。
optimization:使用L1、L2范数度量f(xi)f(x_i)f(xi)和yiy_iyi的差距,即loss function。如何求出参数使得loss function最小?- 偏导数为0。
algorithm:GD、Newton’s method
回归
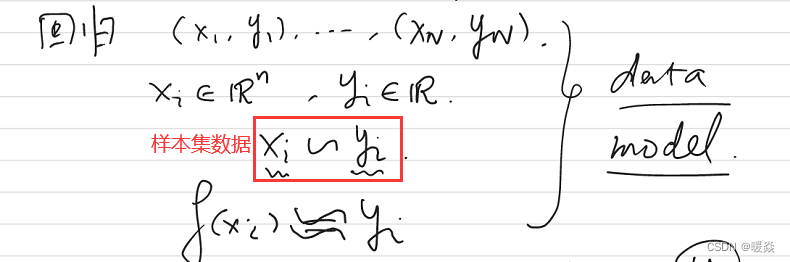



引例:分类
分类
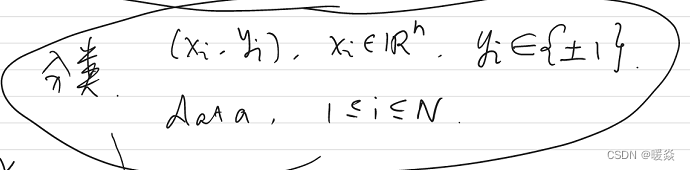
线性可分

FLD

FLD思想:同类点近,不同点远。
根据这个思想,实际的做法是找一条直线,其方向为ω\omegaω,对线性可分的点进行投影,在该直线上,同类点的投影点更近,异类点的投影点更远。进而做一条垂直于该直线的分类线。
先找到投影λ与xi的关系,然后利用w与v垂直内积为0,求出投影λ的表达式,

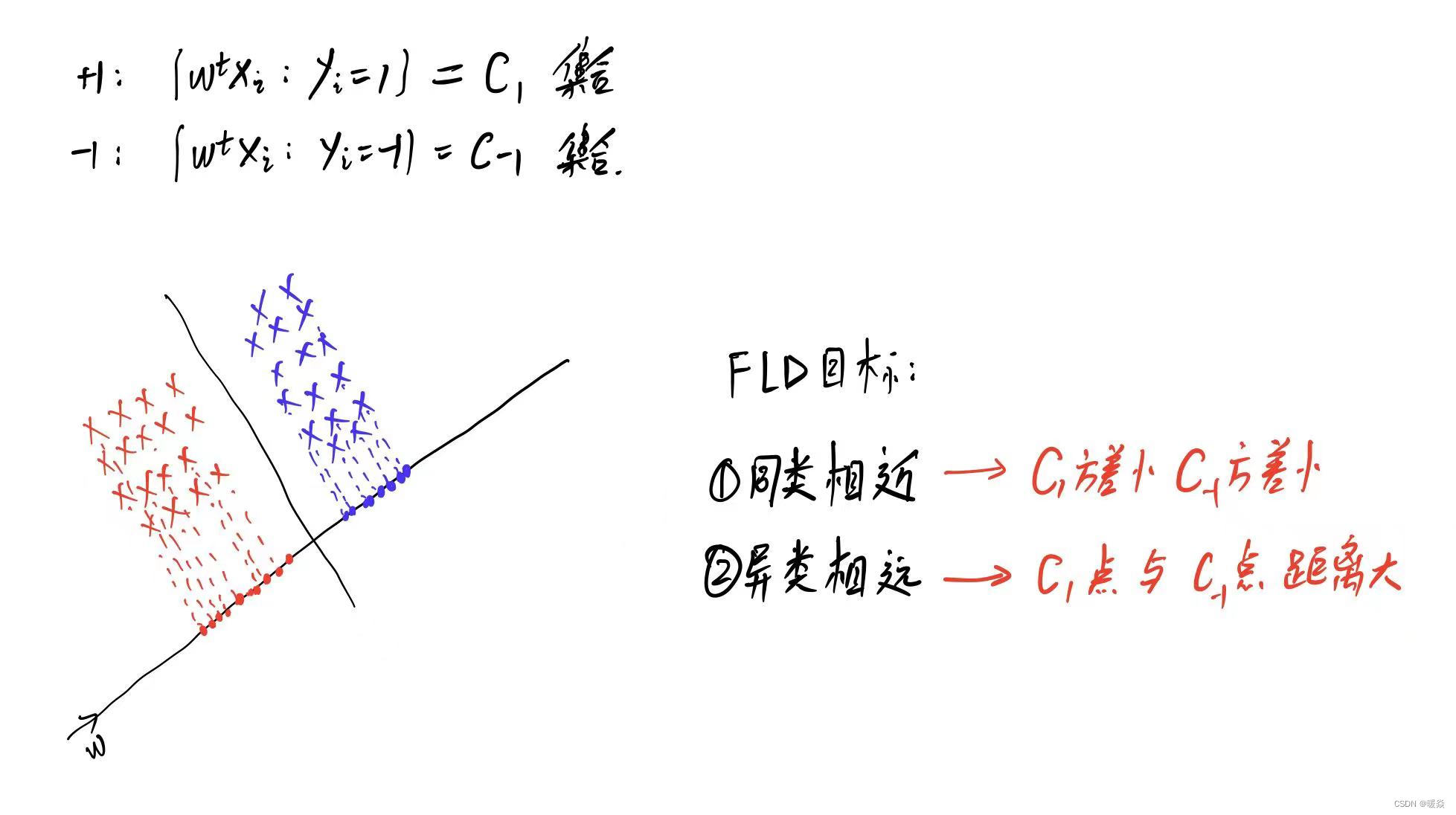

同类相近:要使得C1方差小和C-1的方差小,则将两个优化问题合并为一个优化问题。
异类相远:没有办法计算所有点,所以选择代表性的均值的距离作为两个集合的距离。
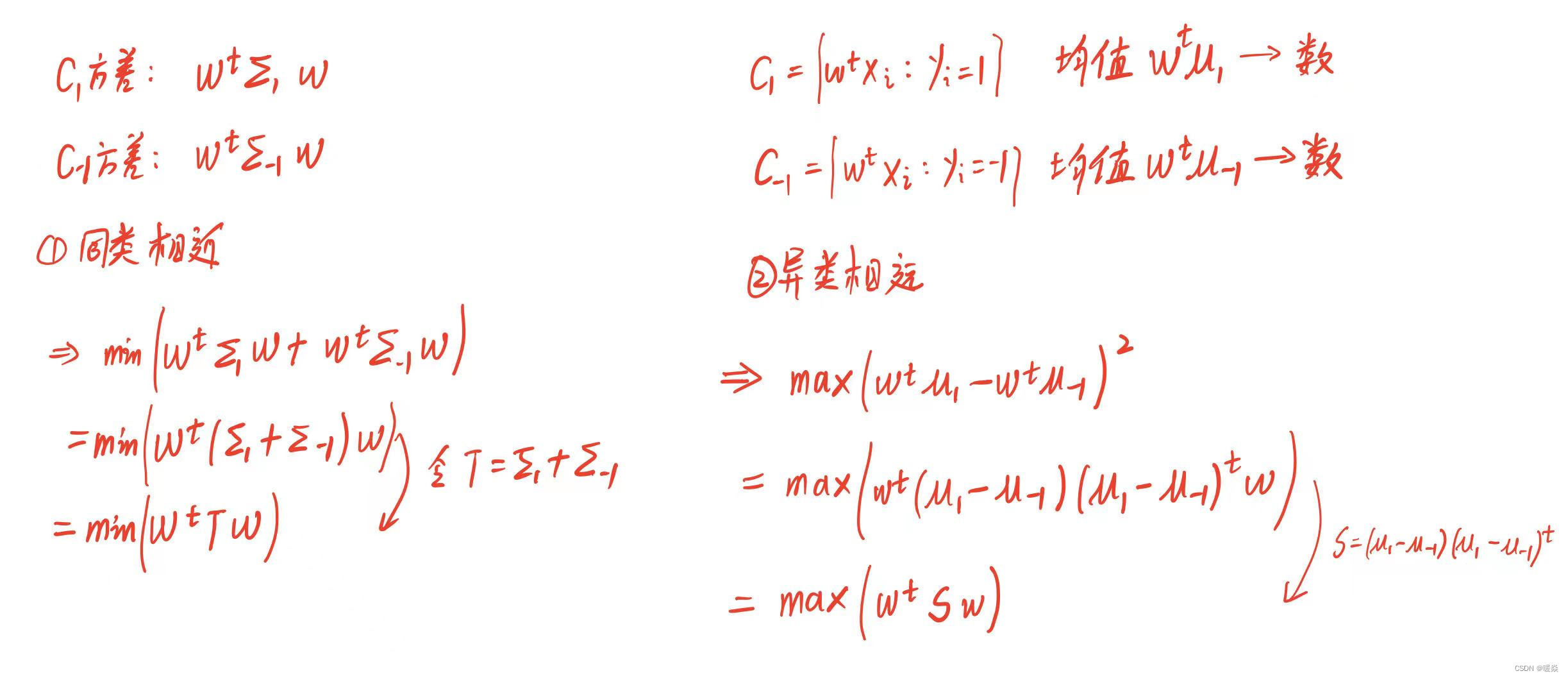
再次将两个优化目标合并为一个单优化目标进行优化。
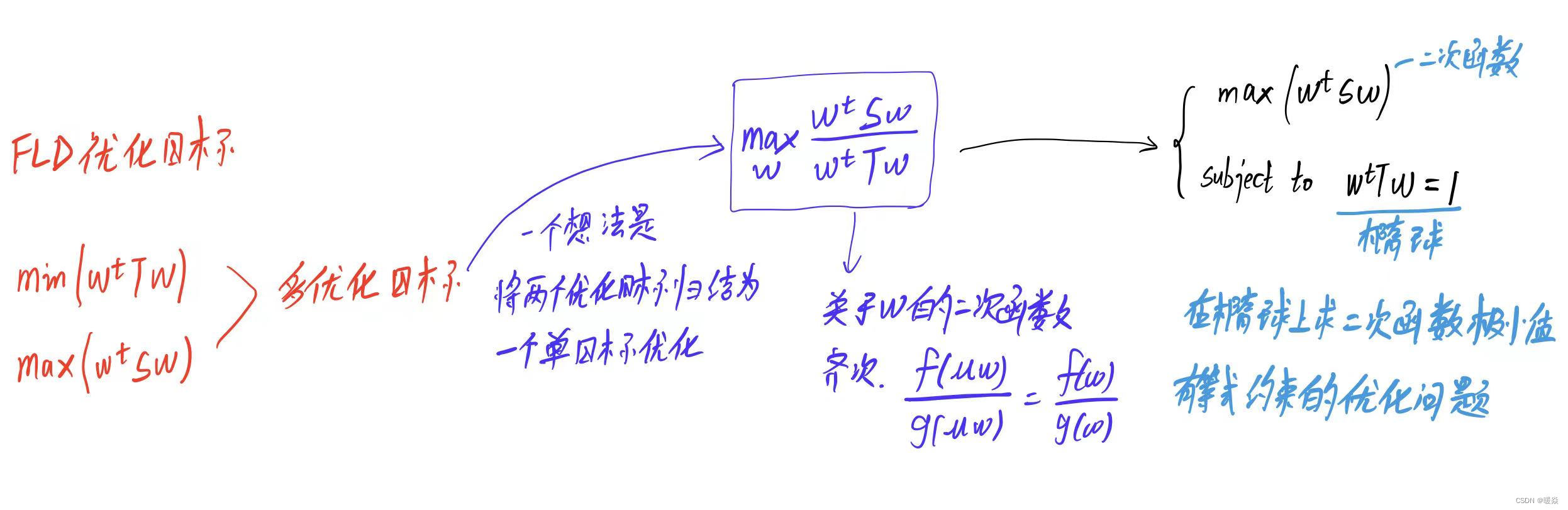
线性不可分
智能计算讨论范围
智能计算讨论的是问题解决流程中的math和optimization。

下降法
为什么要用下降法?- 解析解很难写出公式或很复杂难计算
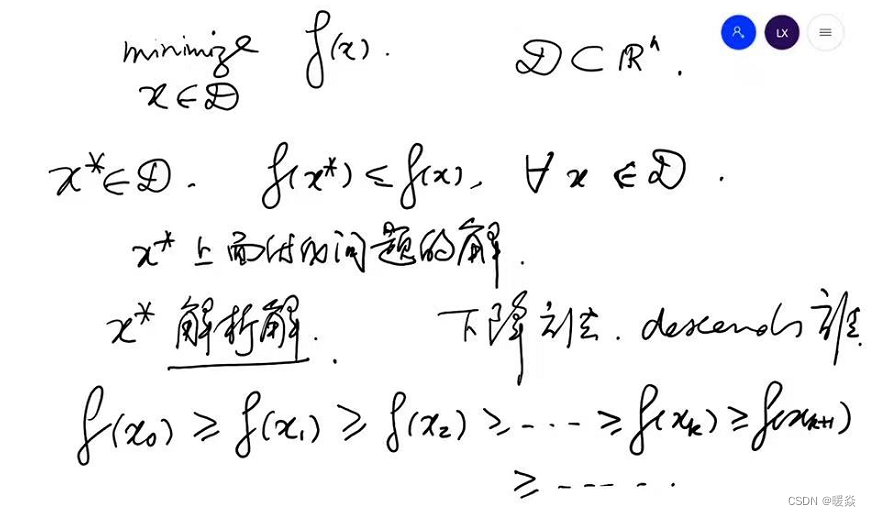
考虑求极值问题场景,需要找到一个x∗x^*x∗使得f(x∗)f(x^*)f(x∗)小于等于邻域内的任意f(x)f(x)f(x),x∗x^*x∗是极小值问题的解,因为x∗x^*x∗的解析解很难写出公式或者可以写出但是公式很复杂难计算,所以考虑使用下降法。
解析解:指通过严格的公式所求得的解。即包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式。给出解的具体函数形式,从解的表达式中就可以算出任何对应值。解析解为一封闭形式的函数,因此对任一独立变量,皆可将其代入解析函数求得正确的相依变量。因此,解析解也称为闭式解。
解析法:用来求得解析解的方法称为解析法,解析法是常见的微积分技巧,如分离变量法等。
下降法亦称极小化方法,是一类重要的迭代法。这类方法将方程组求解问题转化为求泛函极小问题。
使用下降法,找出一系列函数值递减的f(x)f(x)f(x)序列,这个下降过程不是一直持续下去的过程,根据一些停止条件得到一个xkx_kxk时,这个xkx_kxk即优化问题的解x∗x^*x∗。
有哪些常用的下降法?- 梯度下降&高斯-牛顿法
梯度下降(Gradient Descent)- 本质:一阶泰勒展开式近似
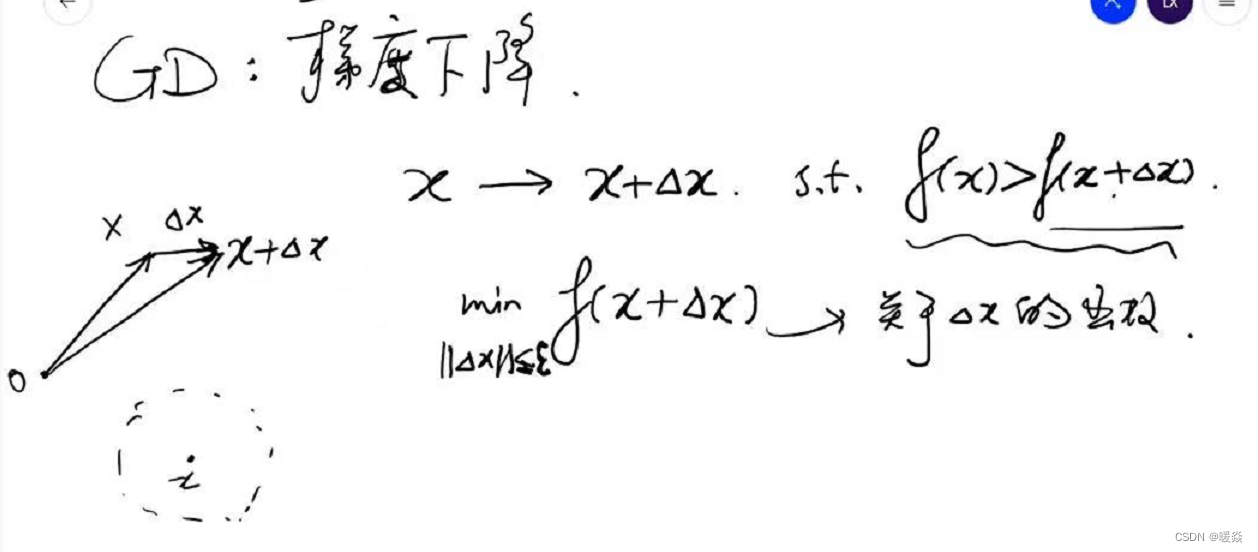
优化问题:在xxx的邻域内,找到一个x+Δxx+ \Delta xx+Δx,使得f(x)>f(x+Δx)f(x)\gt f(x+\Delta x)f(x)>f(x+Δx),且f(x+Δx)f(x+\Delta x)f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小f(x+Δx)f(x+\Delta x)f(x+Δx)?
问题难点:因为f(x)f(x)f(x)优化问题的解析解不容易求解,因此f(x+Δx)f(x+\Delta x)f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑f(x+Δx)f(x+\Delta x)f(x+Δx)的线性近似——一阶泰勒展开式。将min∣∣Δx∣∣≤εf(x+Δx)\underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x)∣∣Δx∣∣≤εminf(x+Δx)问题转换为min∣∣Δx∣∣≤ε(f(x)+atΔx)\underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x)∣∣Δx∣∣≤εmin(f(x)+atΔx),因为min∣∣Δx∣∣≤ε(f(x)+atΔx)\underset {||\Delta x||\le \varepsilon}{min} (f(x)+a^t \Delta x)∣∣Δx∣∣≤εmin(f(x)+atΔx)中f(x)f(x)f(x)是固定的,Δx\Delta xΔx是变量,所以问题可再次简化为min∣∣Δx∣∣≤εatΔx\underset {||\Delta x||\le \varepsilon}{min} a^t \Delta x∣∣Δx∣∣≤εminatΔx。
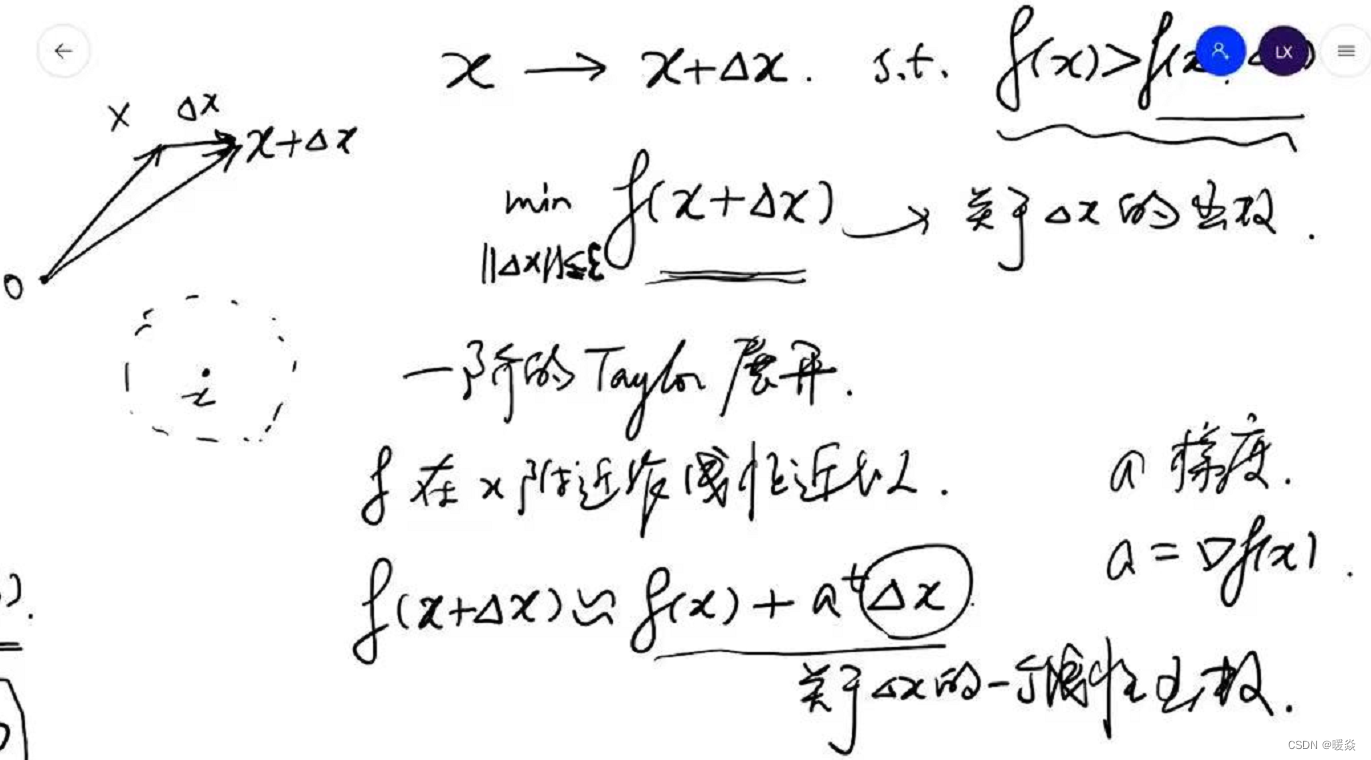
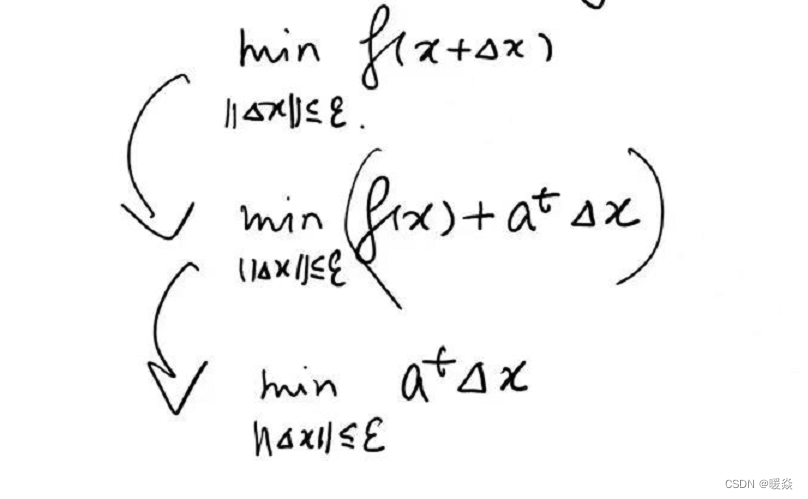
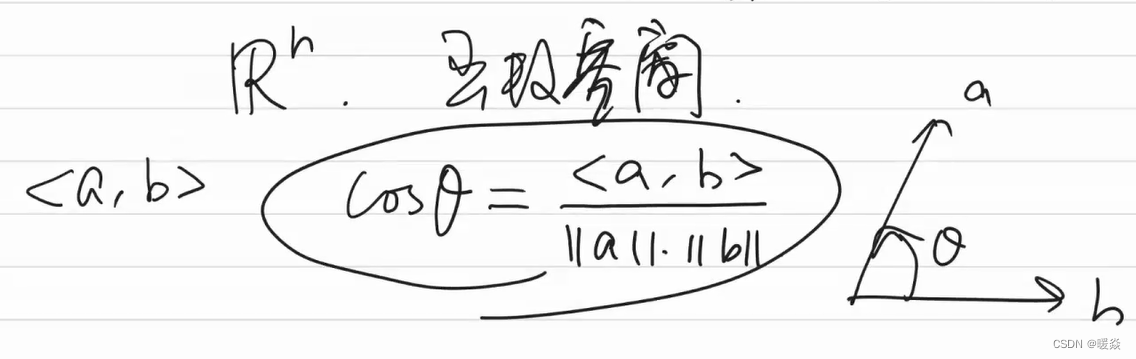
如何找到一阶泰勒展开式的最优解(最小值)?- 柯西一施瓦兹不等式
根据柯西一施瓦兹不等式(Cauchy-Schwarz inequality),atΔxa^t \Delta xatΔx 的最小值是显而易见的。
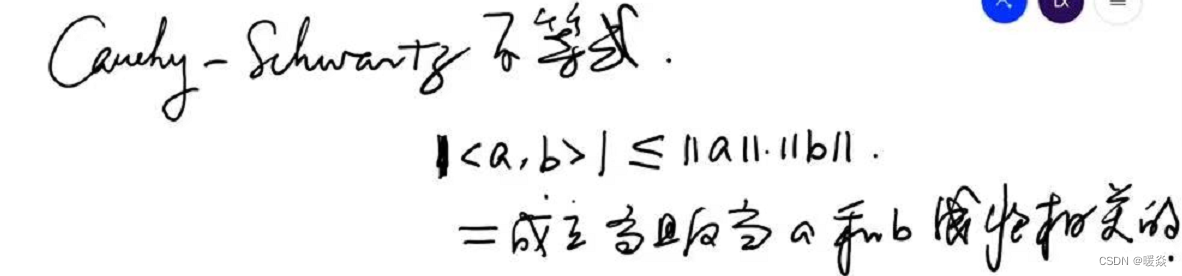
由以上不等式可得:−∣∣a∣∣⋅∣∣b∣∣≤<a,b>≤∣∣a∣∣⋅∣∣b∣∣-||a||·||b|| \le <a,b> \le ||a||·||b||−∣∣a∣∣⋅∣∣b∣∣≤<a,b>≤∣∣a∣∣⋅∣∣b∣∣。
当且仅当a和b共线同向时,a和b线性正相关,<a,b>≤∣∣a∣∣⋅∣∣b∣∣<a,b> \le ||a||·||b||<a,b>≤∣∣a∣∣⋅∣∣b∣∣成立。
当且仅当a和b共线反向时,a和b线性负相关,−∣∣a∣∣⋅∣∣b∣∣≤<a,b>-||a||·||b|| \le <a,b>−∣∣a∣∣⋅∣∣b∣∣≤<a,b>成立。
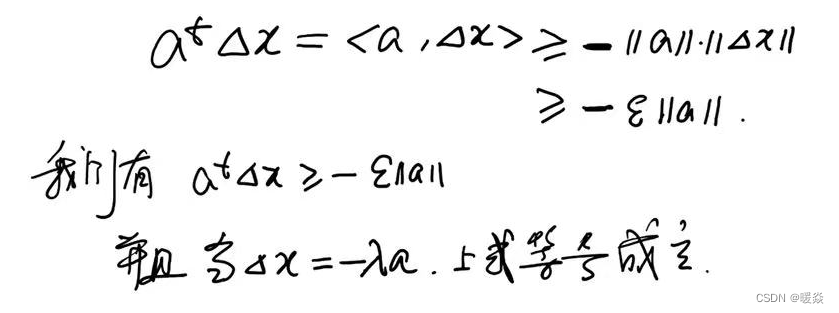
当Δx=−λa\Delta x=-\lambda aΔx=−λa时,表示Δx\Delta xΔx与aaa线性负相关,共线反向,atΔx=−ε∣∣a∣∣a^t \Delta x=-\varepsilon ||a||atΔx=−ε∣∣a∣∣成立。
一阶泰勒展开式中,a表示梯度,所以下降最快的方向为梯度的反方向。
结论:下降最快的方向为梯度的反方向,即梯度下降。
λ\lambdaλ即为学习率。
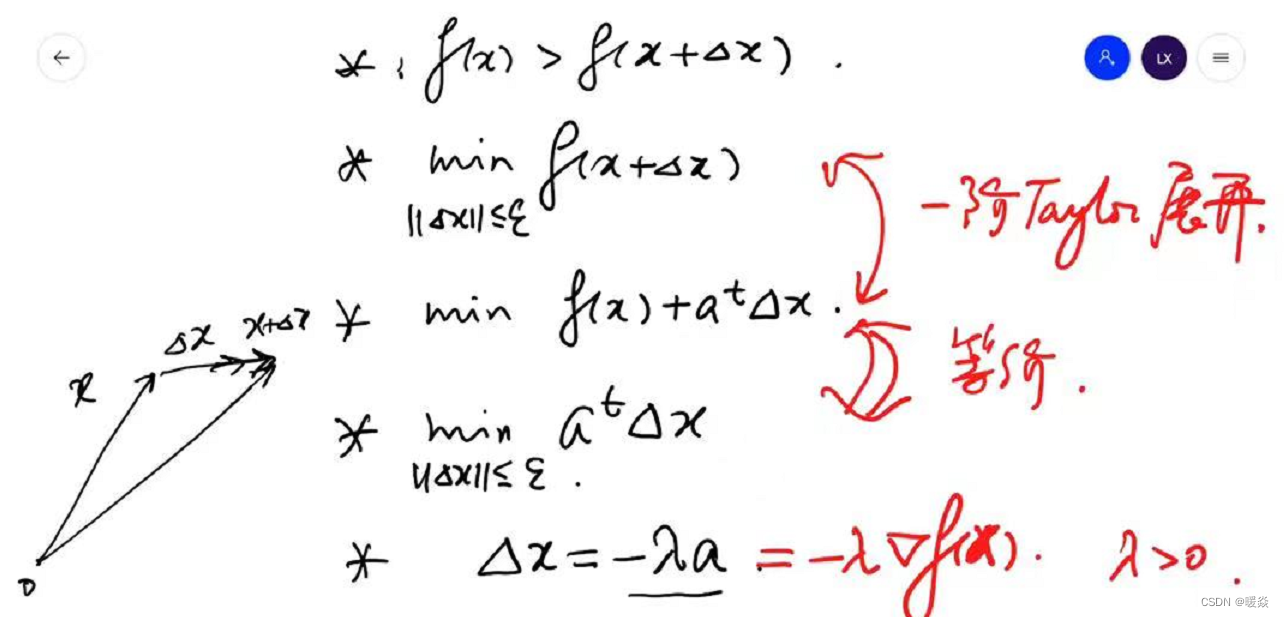
牛顿法 - 本质:二阶泰勒展开式近似
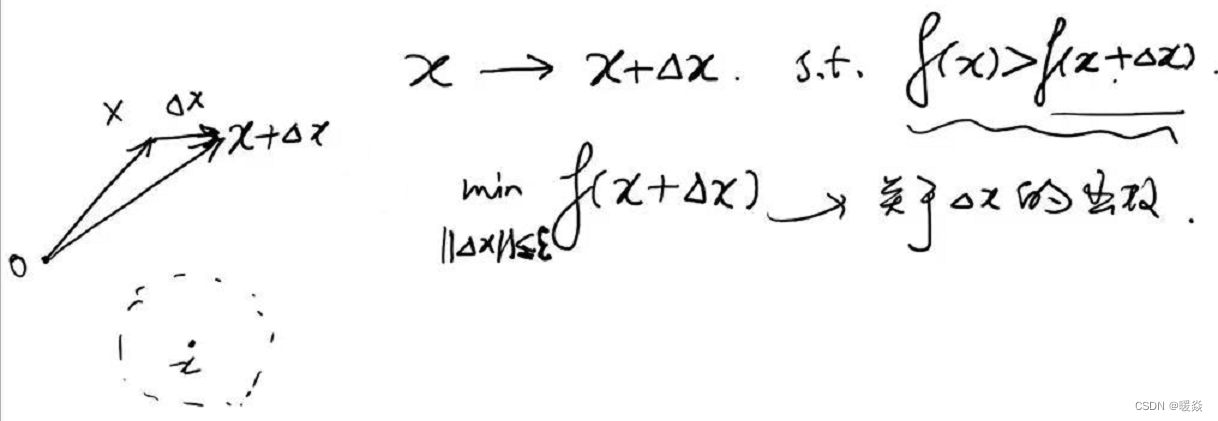
优化问题:在xxx的邻域内,找到一个x+Δxx+ \Delta xx+Δx,使得f(x)>f(x+Δx)f(x)\gt f(x+\Delta x)f(x)>f(x+Δx),且f(x+Δx)f(x+\Delta x)f(x+Δx)在该邻域最小。
数学问题:如何找到该邻域最小f(x+Δx)f(x+\Delta x)f(x+Δx)?
问题难点:因为f(x)f(x)f(x)优化问题的解析解不容易求解,因此f(x+Δx)f(x+\Delta x)f(x+Δx)优化问题的解析解也不容易求解。
解决方法:考虑f(x+Δx)f(x+\Delta x)f(x+Δx)的线性近似——二阶泰勒展开式。将min∣∣Δx∣∣≤εf(x+Δx)\underset {||\Delta x||\le \varepsilon}{min} f(x+\Delta x)∣∣Δx∣∣≤εminf(x+Δx)问题转换为minΔx(f(x)+atΔx+12(Δx)tPΔx)\underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x)Δxmin(f(x)+atΔx+21(Δx)tPΔx),其中f(x)f(x)f(x)是固定的,Δx\Delta xΔx是变量,atΔxa^t \Delta xatΔx是关于Δx\Delta xΔx一次函数,12(Δx)tPΔx)\frac 1 2 (\Delta x)^t P \Delta x)21(Δx)tPΔx)是Δx\Delta xΔx二次函数。
因为使用二阶泰勒展开式近似,f(x+Δx)f(x+\Delta x)f(x+Δx)可看做一个二次函数,可以找到全局最优值,而不需要在邻域中讨论,所以可以删除∣∣Δx∣∣≤ε||\Delta x||\le \varepsilon∣∣Δx∣∣≤ε条件。
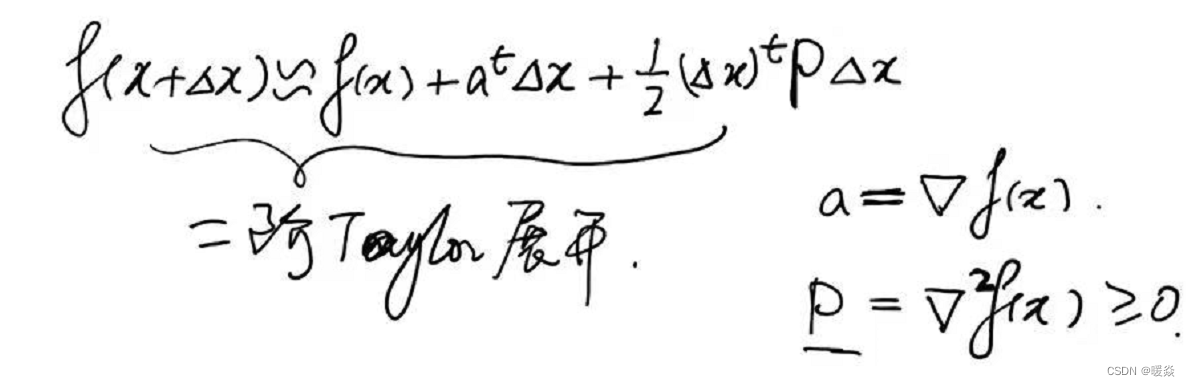
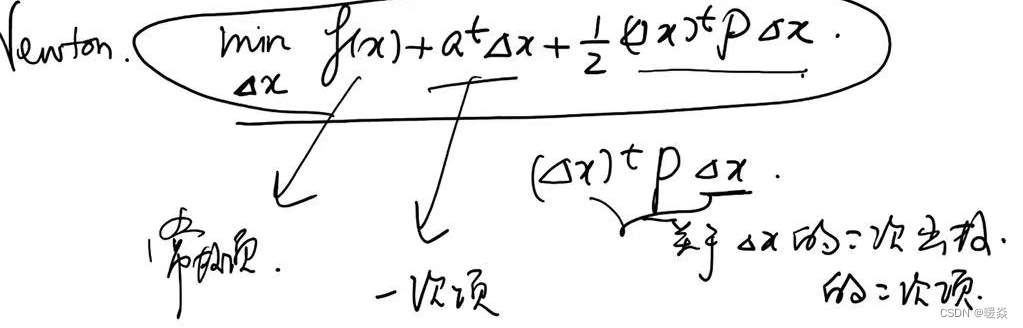
如何找到二阶泰勒展开式的最优解(最小值)?- 梯度=0
令g(Δx)=minΔx(f(x)+atΔx+12(Δx)tPΔx)g(\Delta x)=\underset {\Delta x}{min} (f(x)+a^t \Delta x+\frac 1 2 (\Delta x)^t P \Delta x)g(Δx)=Δxmin(f(x)+atΔx+21(Δx)tPΔx),对g(Δx)g(\Delta x)g(Δx)求关于Δx\Delta xΔx的微分,即梯度∇g\nabla g∇g,令∇g=0\nabla g = 0∇g=0,求出Δx=−P−1a=−(∇2f(x))−1(∇f(x))\Delta x = -P^{-1}a=-(\nabla^2f(x))^{-1}(\nabla f(x))Δx=−P−1a=−(∇2f(x))−1(∇f(x))即为最优解。实际使用时,为了防止(∇2f(x))−1(∇f(x))(\nabla^2f(x))^{-1}(\nabla f(x))(∇2f(x))−1(∇f(x))过大,偏移过远,拟合不准确的问题,需要添加学习率λ\lambdaλ,即Δx=−λ(∇2f(x))−1(∇f(x))\Delta x =-\lambda(\nabla^2f(x))^{-1}(\nabla f(x))Δx=−λ(∇2f(x))−1(∇f(x))。
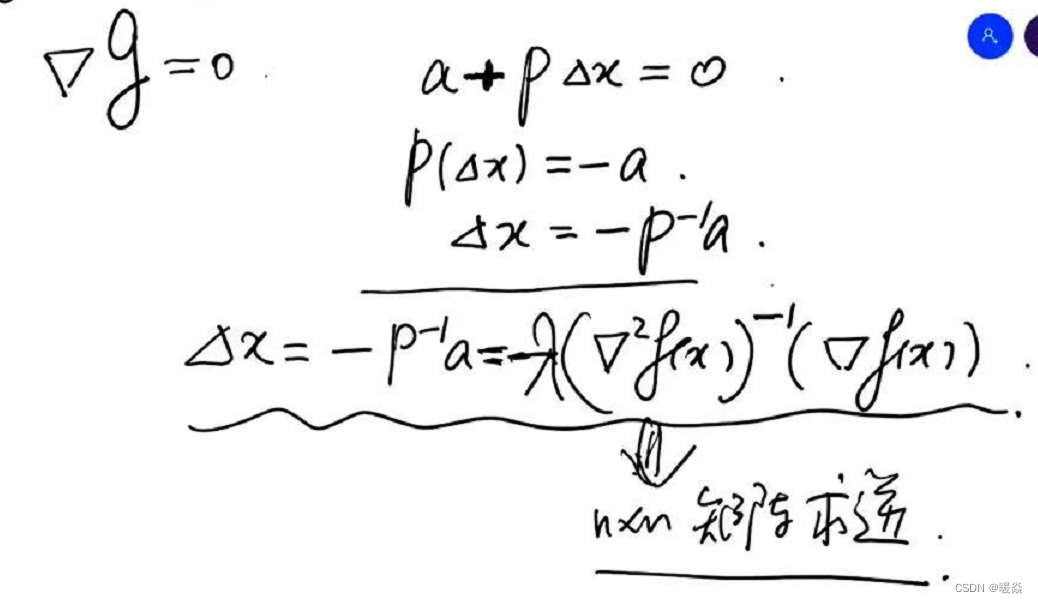
缺点:求解Hessian矩阵的复杂度很高。所以如果Hessian矩阵没有快速计算的方法就会导致迭代过慢,所以牛顿法没有梯度下降法使用频率高。
分类&回归
线性分析
常用不等式
绝对值不等式
∣a1+⋅⋅⋅+an∣≤∣a1∣+⋅⋅⋅+∣an∣|a_1 + · · · + a_n| \le |a_1| + · · · + |a_n|∣a1+⋅⋅⋅+an∣≤∣a1∣+⋅⋅⋅+∣an∣

柯西不等式
<a,b>≤∣∣a∣∣⋅∣∣b∣∣<a,b>\le||a|| \cdot ||b||<a,b>≤∣∣a∣∣⋅∣∣b∣∣
(∑i=1naibi)2≤(∑i=1nai2)(∑i=1nbi2)(\sum_{i=1}^n a_i b_i)^2 \le (\sum_{i=1}^n a_i^2)(\sum_{i=1}^n b_i^2)(∑i=1naibi)2≤(∑i=1nai2)(∑i=1nbi2)
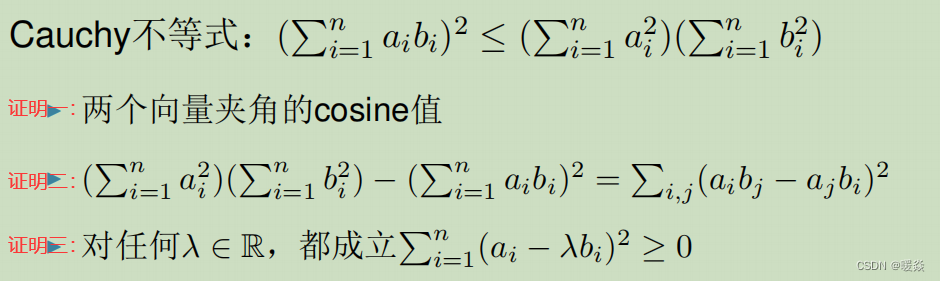

数学研究问题,从群(加)到线性空间(加乘),到赋范线性空间(距离)再到hilbert空间(几何(角度))。
内积的概念很重要,因为有了内积就有了几何结构。
算术-几何平均不等式


数列极限
序列极限
上极限
下极限

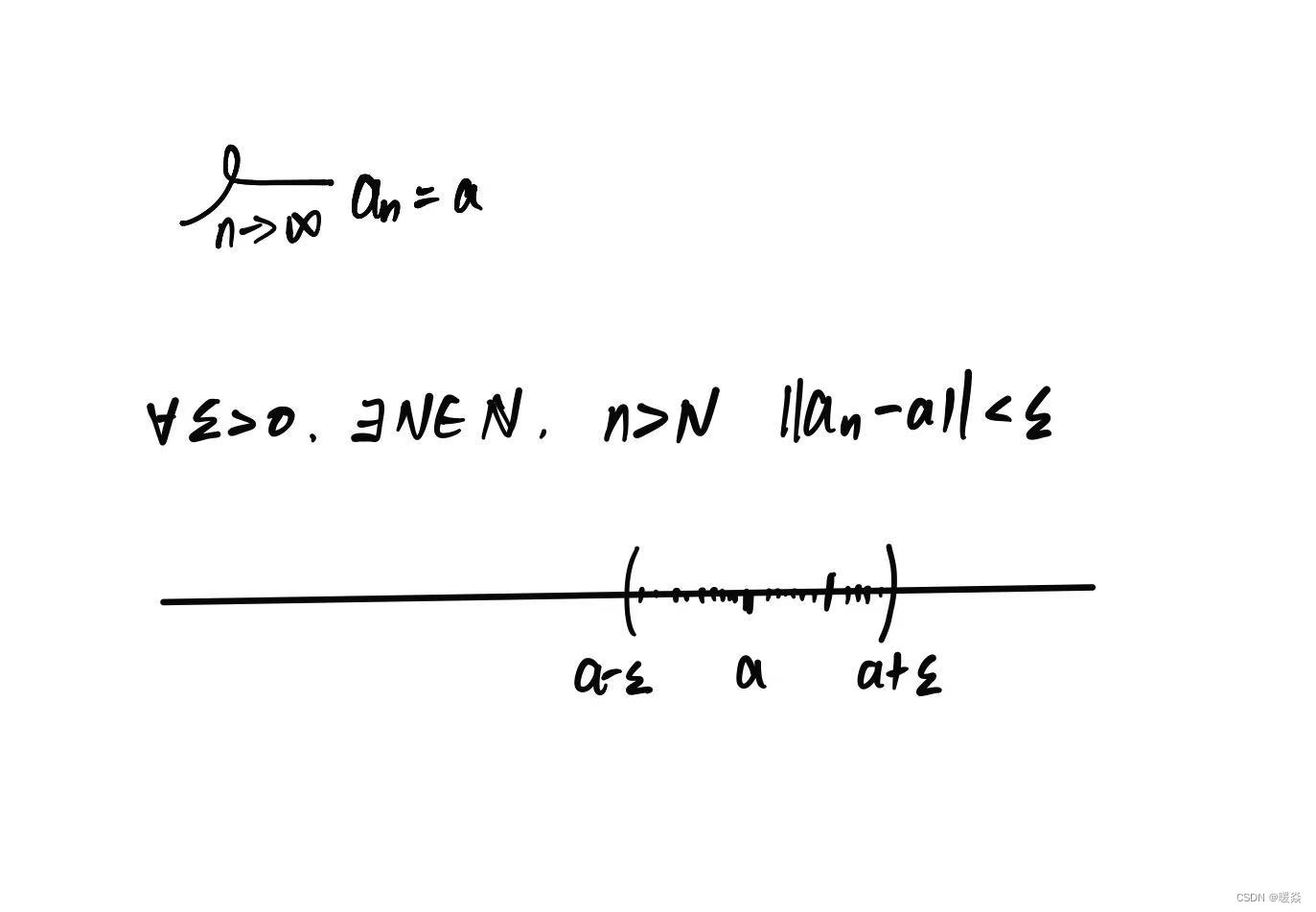
级数
无穷数列和。
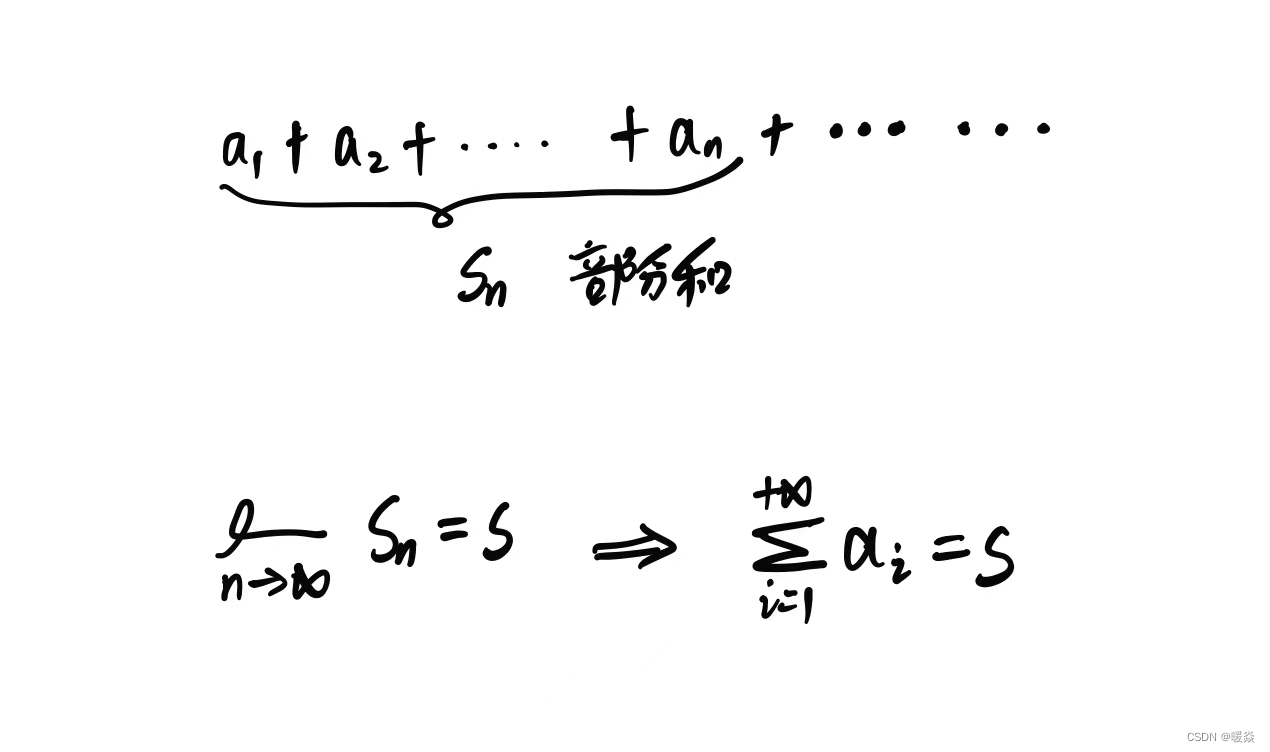

点集拓扑

开集
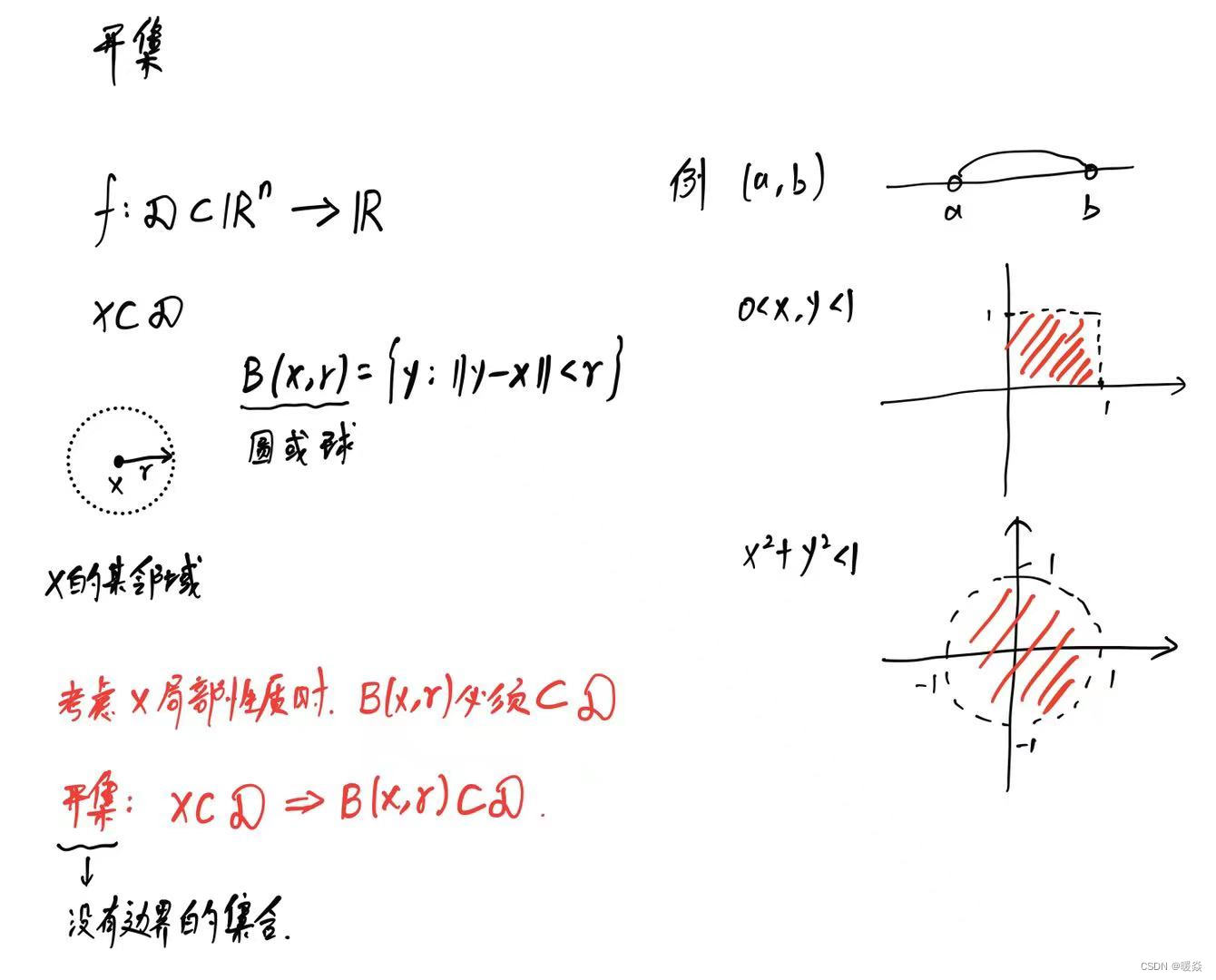
开集性质
任意个开集之并是开集,有限个开集之交是开集。
闭集
“闭”:包含极限点。

闭集性质
任意个闭集之交是闭集,有限个闭集之并是闭集。
紧集
有界闭集。
Heine-Borel定理
Rn\mathbb{R^n}Rn 上紧集的任何开覆盖都存在有限子覆盖。
例题:判断Rn\mathbb{R^n}Rn和∅\emptyset∅是否开闭紧?

Rn\mathbb{R^n}Rn 不是紧集,因为没有边界。
函数连续性
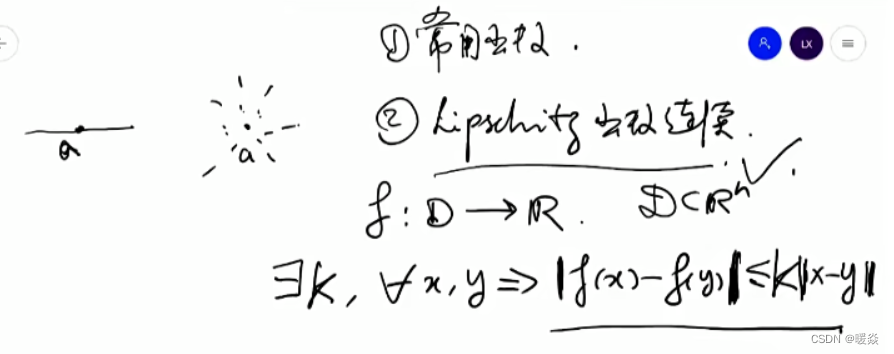
函数连续定义

Lipshitz函数是连续函数

Lipshitz函数与机器学习
参考:Lipschitz函数与机器学习 - gwave的文章 - 知乎
深度学习对输入很敏感,微小的扰动就可能对结果产生很大的影响,将少量精心选择的长臂猿梯度噪声混人熊猫的照片,算法就把熊猫误认为是长臂猿了,Lipschitz常数是种衡量网络稳定性的测度,bound住了输出变化对输入微扰的上限。



连续函数逼近

拉格朗日插值定理


连续函数性质
最值定理

波尔查诺-维尔斯特拉斯定理,又称为致密性定理。指有界数列必有收敛子列。从极限点的角度来叙述致密性定理,就是:有界数列必有极限点。
介值定理
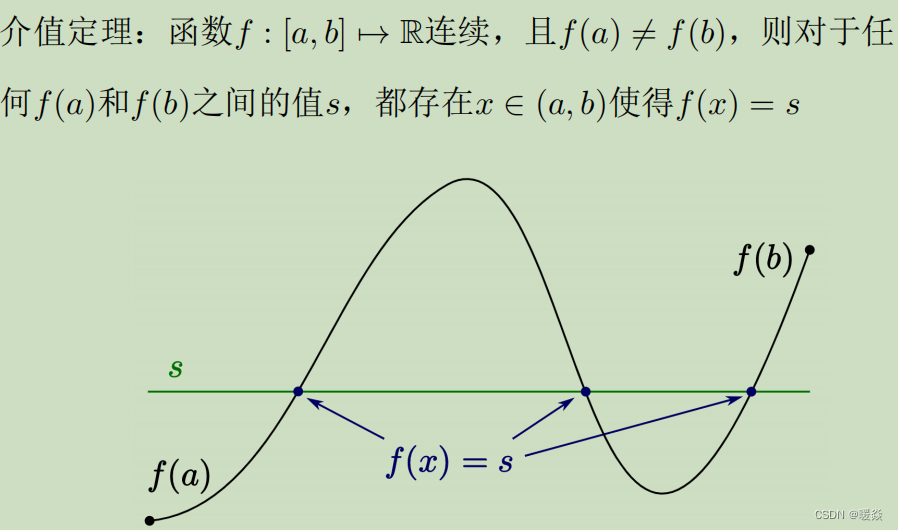
不连续函数

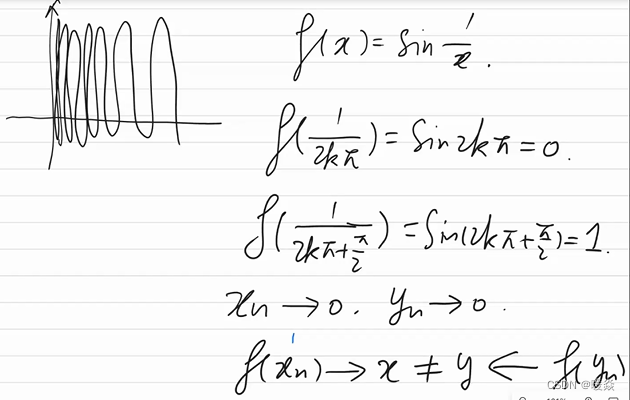
导数
一元函数导数
定义
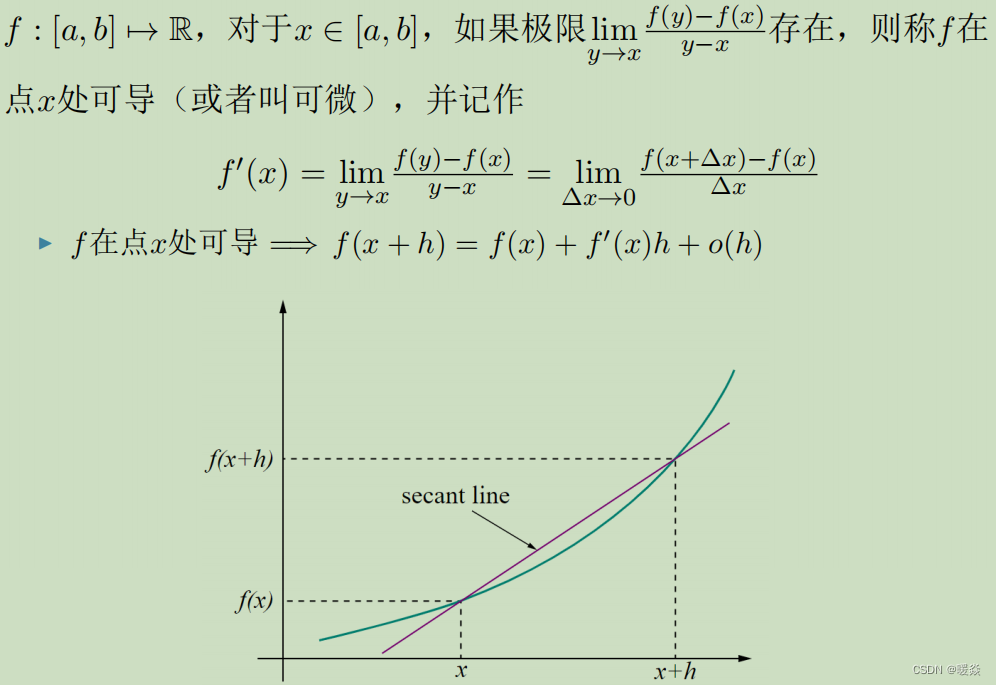
意义

性质
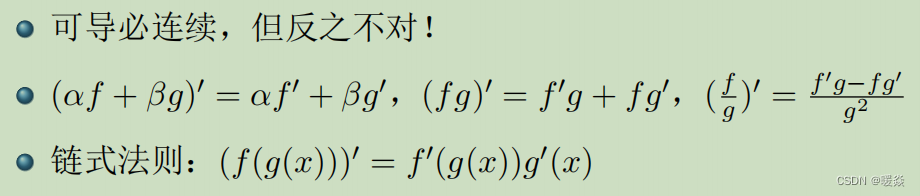
极值定理
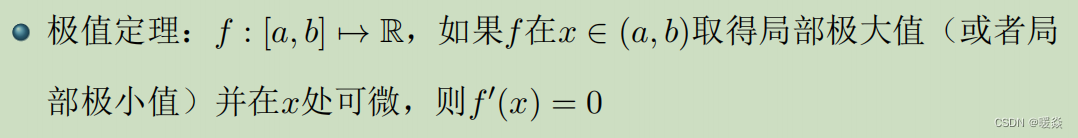
微分中值定理
洛必达法则

常用公式

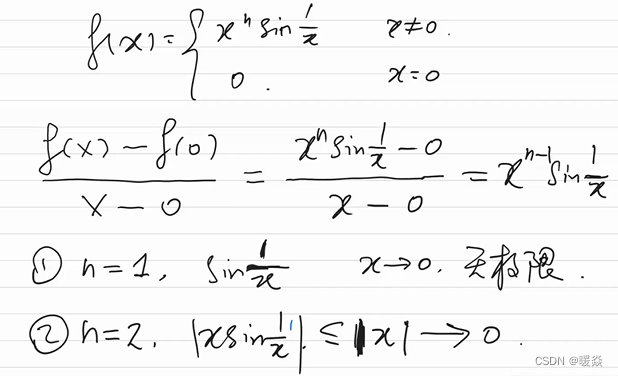
C∞C^\inftyC∞
C1C^1C1:函数一阶导数存在。
C2C^2C2:函数二阶导数存在。
C3C^3C3:函数三阶导数存在。
…
C∞C^\inftyC∞:函数任意阶导数都存在。
多元多值函数
可微
梯度存在
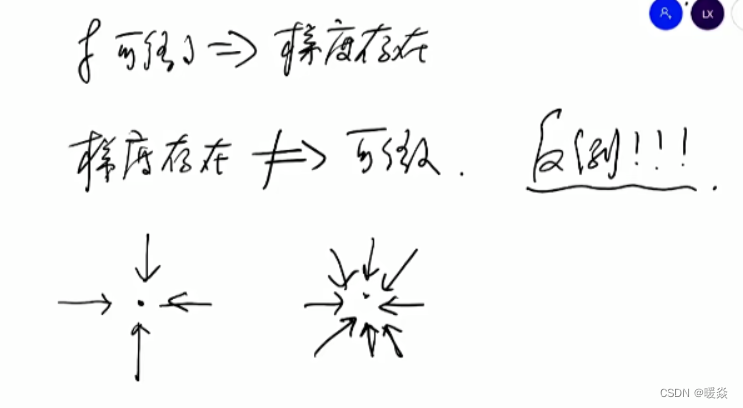
什么情况下梯度存在可以推出函数可微?
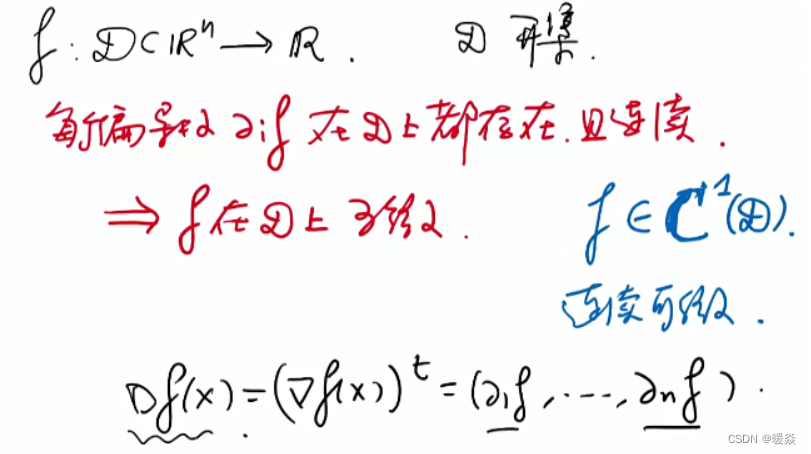

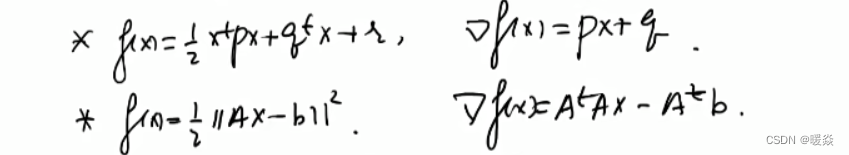


相关文章:

【智能计算数学】微积分
高数问题解决流程引例:回归回归引例:分类分类线性可分FLD线性不可分智能计算讨论范围下降法为什么要用下降法?- 解析解很难写出公式或很复杂难计算有哪些常用的下降法?- 梯度下降&高斯-牛顿法梯度下降(Gradient De…...

win10+RTX4070ti+libtorch部署
环境cuda 11.7、cudnn8.6.0、libtorch1.13.1cu117 注意: 1)libtorch官网进不去的可直接下载 Release version https://download.pytorch.org/libtorch/cu117/libtorch-win-shared-with-deps-1.13.1%2Bcu117.zip Debug version https://download.pytorch.…...

【Python百日进阶-Web开发-Vue3】Day518 - Vue+ts后台项目5:用户列表
文章目录 一、获取用户列表的数据1.1 定义用户列表和角色列表的接口src/request/api.ts1.2 获取用户列表数据src/views/UserView.vue二、定义用户列表数据类型2.1 src/type/user.ts三、展示用户列表内容3.1 element-plus中的Select 选择器3.2 element-plus中的表格插槽3.3 展示…...

Linux内核转储---kdump原理梳理
文章目录Kexec和Kdump设计的区别kexeckdumpKdump的执行流程kexec的实现用户空间kexec内核空间vmcoreKdump的实现可以分为两部分:内核和用户工具。内核提供机制,用户工具在这些机制上实现各种转储策略,内核机制对用户工具的接口是一个系统调用…...
【C++】从0到1入门C++编程学习笔记 - 实战篇:演讲比赛流程管理系统
文章目录一、演讲比赛程序需求1.1 比赛规则1.2 程序功能1.3 程序效果图:二、项目创建2.1 创建项目2.2 添加文件三、创建管理类3.1创建文件3.2 头文件实现3.3 源文件实现四、菜单功能4.1 添加成员函数4.2 菜单功能实现4.3 测试菜单功能五、退出功能5.1 提供功能接口5…...

04 OpenCV位平面分解
1 基本概念 位平面分解的核心思想是将图像的每一个像素分解为多个二进制位,分别存储在不同的位平面上。例如,如果一个图像是8位深度的,则可以分解为8个位平面,每个位平面上存储一个二进制位。 位平面分解在图像压缩中有着重要的…...
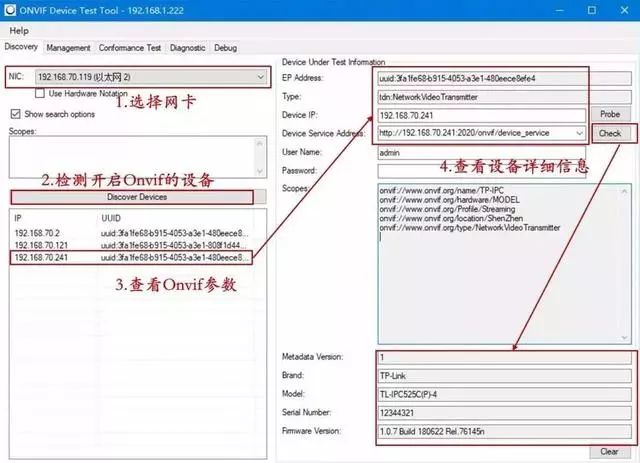
Onvif协议如何判断摄像机支持 —— 筑梦之路
有人就问什么是Onvif协议呢? 全称为:Open Network Video Interface Forum.缩写成Onvif。 翻译过来是:开放型网络视频接口论坛,目的是确保不同安防厂商的视频产品能够具有互通性,这样对整体安防行业才是良性发展。 现…...

情人节new一个对象给你
今天情人节,有没对象的吗?假设你不知道new怎么用,每个人都有两种身份,一种没对象的人,这个时候new一个对象给你,一种是有对象的人,这个delete对象。等你学完这个new和delete知识点,无…...
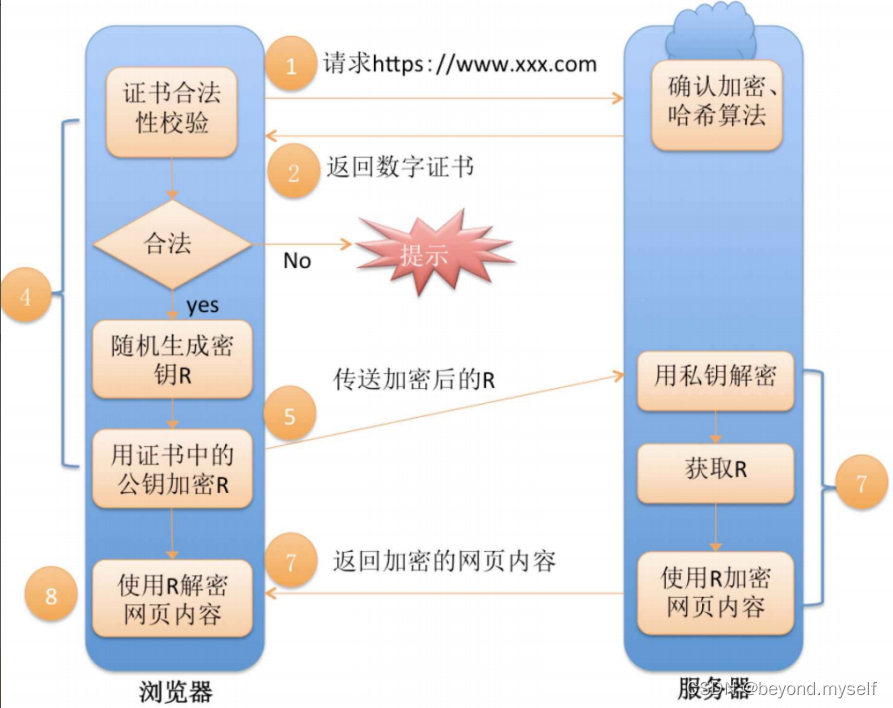
linux篇【15】:应用层-网络https协议
目录 一.HTTPS介绍 1.HTTPS 定义 2.HTTP与HTTPS (1)端口不同,是两套服务 (2)HTTP效率更高,HTTPS更安全 3.加密,解密,密钥 概念 4.为什么要加密? 5.常见的加密方式…...

索引-性能分析-explain
explain 执行计划 explain 执行计划各字段含义 1)id 就是代表 sql 的执行顺序或者表的执行顺序;id相同从上往下执行,id不同,id值越大越先执行;(注:有子查询时就会出现sql执行顺序)…...

mbedtls加密组件使用示例
1 mbedtls aes组件的使用 1.1 AES ECB加解密接口使用 int main(int argc, char *argv[]) {char key[256];char *inbuf calloc(1, 257);char *outbuf calloc(1, 257);char *buf calloc(1,257);char *tmp_outbuf outbuf;char *tmp_buf buf;mbedtls_aes_context aes_ctx;mb…...

如何量测太阳光模拟器的光谱致合度?
太阳模拟器是根据国际法规JIS、IEC60904、美国材料试验协会开发设计的AAA级太阳模拟器。对于100毫米100毫米和200毫米200毫米的光斑尺寸,光斑强度的输出功率范围可以从0.1到1太阳光强度。此外,还提供了灵活的出光方向,以满足用户的研究需求&a…...

网络安全领域中CISP证书八大类都有什么
CISP注册信息安全专业人员 注册信息安全专业人员(Certified Information Security Professional),是经中国信息安全产品测评认证中心实施的国家认证,对信息安全人员执业资质的认可。该证书是面向信息安全企业、信息安全咨询服务…...
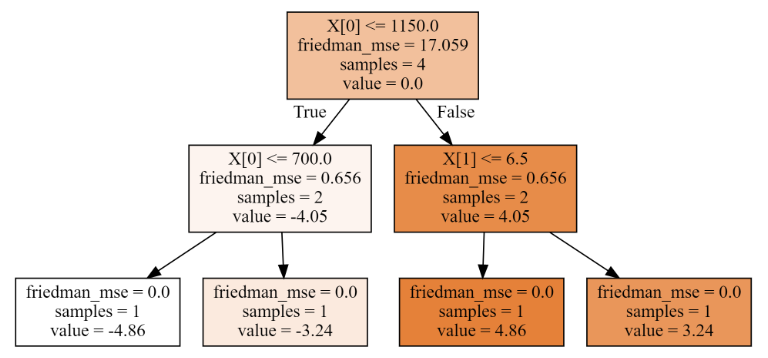
17- 梯度提升回归树GBRT (集成算法) (算法)
梯度提升回归树: 梯度提升回归树是区别于随机森林的另一种集成方法,它的特点在于纠正与加强,通过合并多个决策树来构建一个更为强大的模型。该模型即可以用于分类问题,也可以用于回归问题中。在该模型中,有三个重要参数分别为 n_…...

05 OpenCV色彩空间处理
色彩空间(Color Space)是一种用于描述颜色的数学模型,它将颜色表示为多维向量或坐标,通常由三个或四个独立的分量来表示。不同的色彩空间在颜色的表示方式、可表达颜色的范围、计算速度和应用场景等方面存在差异,不同的…...
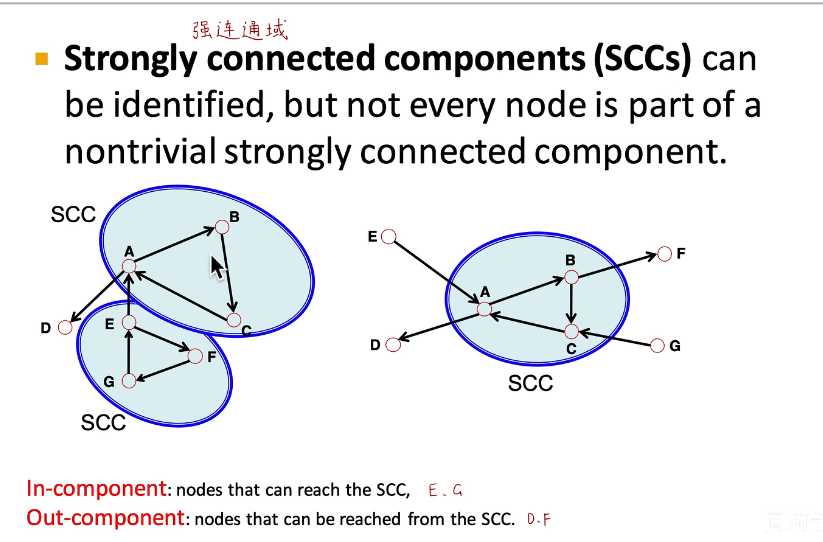
【CS224图机器学习】task1 图机器学习导论
前言:本期学习是由datawhale(公众号)组织,由子豪兄讲解的202302期CS224图机器学习的学习笔记。本次学习主要针对图机器学习导论做学习总结。1.什么是图机器学习?通过图这种数据结构,对跨模态数据进行整理。…...
Powershell Install SQL Server 2022
前言 SQL Server 2022 (16.x) 在早期版本的基础上构建,旨在将 SQL Server 发展成一个平台,以提供开发语言、数据类型、本地或云环境以及操作系统选项。 SQL Server Management Studio (SSMS) 是一种集成环境,用于管理从 SQL Server 到 Azure SQL 数据库的任何 SQL 基础结构…...

Jetson NX2 装机过程
1.固态硬盘安装完成后,系统配置 df -h 查看硬盘使用情况 2.查看Jetson NX的IP地址,以下两个都行 ifconfig ip address show 3.Jetson NX2安装arm64的annaconda3,安装有问题报错illegal instruction,未解决。 4.VNC远程登录 …...

初始C++(四):内联函数
文章目录一.内联函数概念二.内联函数用法三.内联函数的特性四.内联函数和宏一.内联函数概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调用建立栈帧的开销,内联函数提升程序运行的效率。 二.内联函…...

九、初识卷积
文章目录1、通过边缘检测认识卷积2、Padding3、Strid Convelution4、RGB图像的卷积THE END1、通过边缘检测认识卷积 \qquad在使用神经网络进行图像识别时,神经网络的前几层需要完成对图像的边缘检测任务,所谓的边缘检测就是让计算机识别出一张图片的垂直…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...