Leetcode.1124 表现良好的最长时间段
题目链接
Leetcode.1124 表现良好的最长时间段 Rating : 1908
题目描述
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
示例 2:
输入:hours = [6,6,6]
输出:0
提示
- 1<=hours.length<=1041 <= hours.length <= 10^41<=hours.length<=104
- 0<=hours[i]<=160 <= hours[i] <= 160<=hours[i]<=16
分析:
问题转化:工作时间大于8h 看作+1,工作时间 小于等于 8h 看作 -1。所以原问题转化为 求一段连续的区间 [l,r],这个区间和是大于0的,且区间长度最大。
我们用 前缀和 可以在 O(1)O(1)O(1) 的复杂度求出一段连续区间的和。
如果我们暴力枚举 n-1个左端点,寻找最长的区间和sum > 0的区间,会超时…
为此我们使用一个 单调栈 来记录,所有可能的左端点。
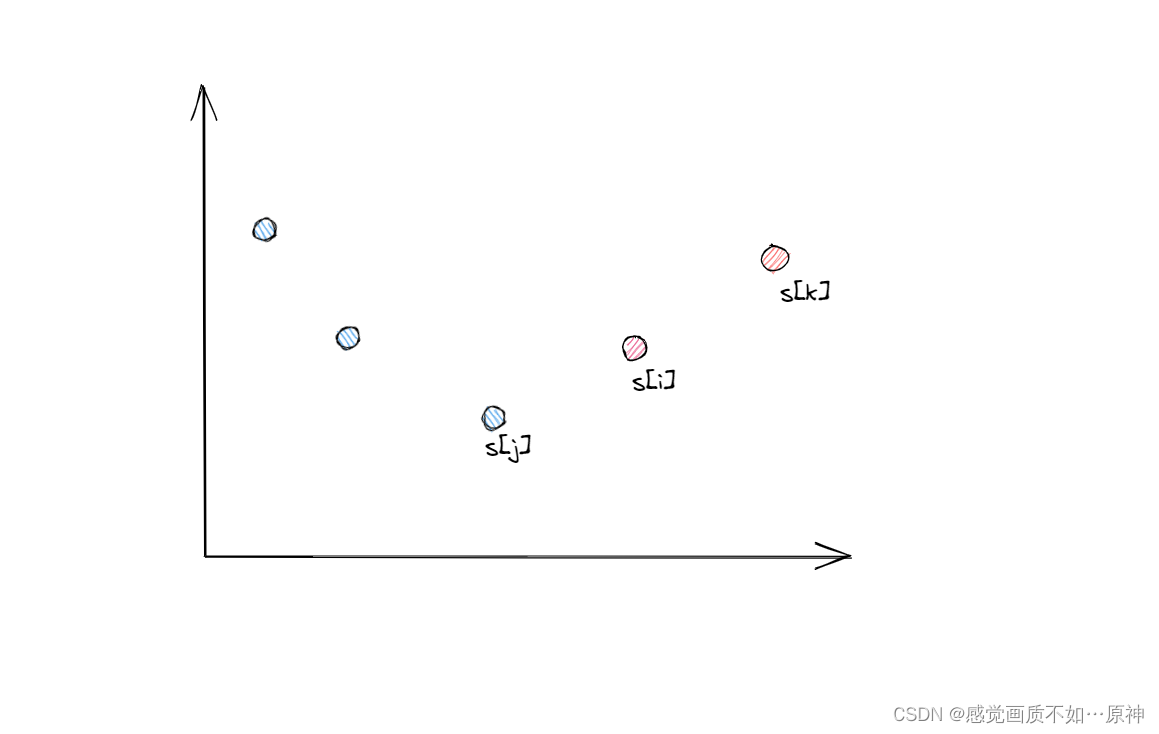
当遍历到 s[i]s[i]s[i] 时,如果 s[j]<s[i]s[j] < s[i]s[j]<s[i],说明 s[j]s[j]s[j] 就可能称为一个左端点。
如果想让 s[i]s[i]s[i] 也有成为左端点的可能,后面必然有一个 s[k]>s[i]s[k] > s[i]s[k]>s[i],但是这样的话 s[k]>s[j]s[k] > s[j]s[k]>s[j],s[i]s[i]s[i] 相比 s[j]s[j]s[j] 更可能成为一个左端点。
所以栈 stk中,要记录的就是这样的点,栈中的元素是从 栈底到栈顶 依次递减的。
最后,我们倒序遍历 前缀和数组s,如果当前的s[i]大于 栈顶元素 s[stk.top()],就更新最大值。
时间复杂度:O(n)O(n)O(n)
代码:
class Solution {
public:int longestWPI(vector<int>& hours) {int n = hours.size();//前缀和数组int s[n+1];s[0] = 0;stack<int> st;//先插入0,处理边界情况st.push(0);for(int i = 1;i <= n;i++){s[i] = s[i-1] + (hours[i-1] > 8 ? 1 : -1);if(s[st.top()] > s[i]) st.push(i);}int ans = 0;for(int i = n;i >= 1;--i){while(!st.empty() && s[i] > s[st.top()]){ans = max(ans , i - st.top());st.pop();}}return ans;}
};
相关文章:

Leetcode.1124 表现良好的最长时间段
题目链接 Leetcode.1124 表现良好的最长时间段 Rating : 1908 题目描述 我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。 所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格…...

达梦数据库会话、事务阻塞排查步骤
查询阻塞的事务IDselect * from v$trxwait order by wait_time desc;--单机select * from v$dsc_trxwait order by wait_time desc;–DSC集群查询阻塞事务的会话信息select sf_get_session_sql(sess_id),* from v$sessions where trx_id69667;--单机select sf_get_session_sql(…...

sqlServer 2019 开发版(Developer)下载及安装
下载软件 官网只有2022的,2019使用百度网盘进行下载 安装下崽器 选择自定义安装 选择语言、以及安装位置 点击“安装” 安装 SQL Server 可能的故障 以上步骤安装后会弹出以上界面,如果未弹出,手动去安装目录下点击 SETUP.EXE 文件…...
使用Arthas定位问题
功能概述 首先,Arthas的常用功能大概有以下几个: 解决依赖冲突 sc命令:模糊查看当前 JVM 中是否加载了包含关键字的类,以及获取其完全名称。 sc -d 关键字 注意使用 sc -d 命令,获取 classLoaderHash命令:…...
性能测试之tomcat+nginx负载均衡
nginx tomcat 配置准备工作:两个tomcat 执行命令 cp -r apache-tomcat-8.5.56 apache-tomcat-8.5.56_2修改被复制的tomcat2下conf的server.xml 的端口号,不能与tomcat1的端口号重复,不然会启动报错 ,一台电脑上想要启动多个tomcat,…...
【手写 Vuex 源码】第十一篇 - Vuex 插件的开发
一,前言 上一篇,主要介绍了 Vuex-namespaced 命名空间的实现,主要涉及以下几个点: 命名空间的介绍和使用;命名空间的逻辑分析与代码实现;命名空间核心流程梳理; 本篇,继续介绍 Vu…...

opencv基础知识和绘图图形
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

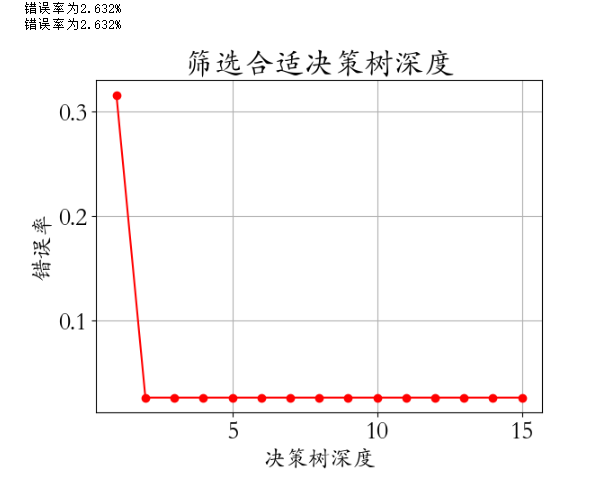
15- 决策回归树, 随机森林, 极限森林 (决策树优化) (算法)
1. 决策回归树: from sklearn.tree import DecisionTreeRegressor model DecisionTreeRegressor(criterionmse,max_depth3) model.fit(X,y) # X是40个点 y是一个圆 2. 随机森林 稳定预测: from sklearn.ensemble import RandomForestClassifier # model RandomForestC…...

Flink相关的记录
Flink源码编译首次编译的时候,去除不必要的操作,同时install会把Flink中的module安装到本地仓库,这样依赖当前module的其他组件就无需去远程仓库拉取当前module,节省了时间。mvn clean install -T 4 -DskipTests -Dfast -Dmaven.c…...
配置可视化-基于form-render的无代码配置服务(一)
背景 有些业务场景需要产品或运营去配置JSON数据提供给开发去使用(后面有实际业务场景的说明),原有的业务流程,非开发人员(后面直接以产品指代)把数据交给开发,再由开发去更新JSON数据。对于产…...
Java 代理模式详解
1、代理模式 代理模式是一种比较好理解的设计模式。简单来说就是 我们使用代理对象来代替对真实对象(real object)的访问,这样就可以在不修改原目标对象的前提下,提供额外的功能操作,扩展目标对象的功能。 代理模式的主要作用是扩展目标对象…...
知识付费小程序怎么做_分享知识付费小程序的作用
在线知识付费产业的主要业务逻辑是基于用户的主动学习需求,为其提供以跨领域基础知识与技能为核心的在线知识服务,提升其达到求知目的的效率。公众号和小程序的迅速发展,又为知识付费提供了技术支持,从而促进了行业的进一步发展。…...
14- 决策树算法 (有监督学习) (算法)
决策树是属于有监督机器学习的一种决策树算法实操: from sklearn.tree import DecisionTreeClassifier # 决策树算法 model DecisionTreeClassifier(criterionentropy,max_depthd) model.fit(X_train,y_train)1、决策树概述 决策树是属于有监督机器学习的一种,起源…...

如何编译和运行C++程序?
C 和C语言类似,也要经过编译和链接后才能运行。在《C语言编译器》专题中我们讲到了 VS、Dev C、VC 6.0、Code::Blocks、C-Free、GCC、Xcode 等常见 IDE 或编译器,它们除了可以运行C语言程序,还可以运行 C 程序,步骤是一样的&#…...

Golang 给视频添加背景音乐 | Golang工具
目录 前言 环境依赖 代码 总结 前言 本文提供给视频添加背景音乐,一如既往的实用主义。 主要也是学习一下golang使用ffmpeg工具的方式。 环境依赖 ffmpeg环境安装,可以参考我的另一篇文章:windows ffmpeg安装部署_阿良的博客-CSDN博客 …...

让AI护理医疗:解决卫生系统的痛点
一、引言 1.对医疗领域中AI技术的介绍 随着人工智能的不断发展,它已经成为了各个领域中的重要组成部分。在医疗领域中,AI技术也逐渐发挥着越来越重要的作用。从诊断到治疗,从健康管理到研究,人工智能已经深刻地影响着医疗领域的…...
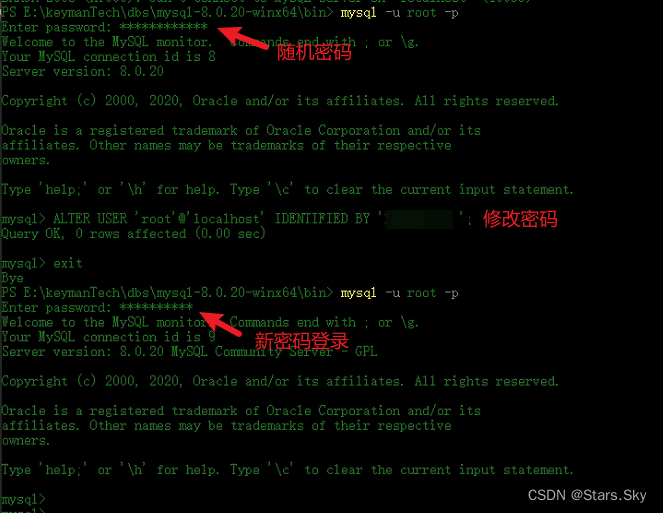
Windows 离线安装 MySQL 8
目录 1. 下载离线安装包 2. 上传解压 3 配置 my.ini 文件 4 设置系统环境变量 5 安装 MySQL 6 登录 MySQL 客户环境是内网环境,不能访问外网,只能离线安装 MySQL 了。 1. 下载离线安装包 MySQL 离线压缩包官网下载地址:MySQL :: Down…...

【前端攻城狮之vue基础】02路由+嵌套路由+路由query/params传参+路由props配置+replace属性+编程式路由导航+缓存路由组件
路由的基础知识1.路由简介2.路由基本使用3.嵌套路由4.传递路由的query传参# 5.传递路由的params参数6.路由的props传参配置7.路由router-link标签的replace属性8.编程式路由导航9.缓存路由组件1.路由简介 路由是一条条对应的key-value关系,key就是前端地址栏的路径…...
CHAPTER 1 Zabbix介绍及安装
Zabbix介绍及安装1.1 Zabbix监控1 为什么要监控1.1 网站可用性2 监控什么东西2.1 监控范畴3 怎么来监控3.1 远程管理服务器3.2 监控硬件3.3 查看cpu相关3.4 内存3.5 磁盘3.6 监控网络4 监控工具总览5 zabbix介绍5.1 zabbix的组成5.2 zabbix监控范畴1.2 安装zabbix1 环境检查2 安…...

认识V模型、W模型、H模型
软件测试与软件工程息息相关,软件测试是软件工程组成中不可或缺的一部分。 在软件工程、项目管理、质量管理得到规范化应用的企业,软件测试也会进行得比较顺利,软件测试发挥的价值也会更大。 要关注软件工程、质量管理以及配置管理与软件测试…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
