Leetcode-每日一题1250. 检查「好数组」(裴蜀定理)
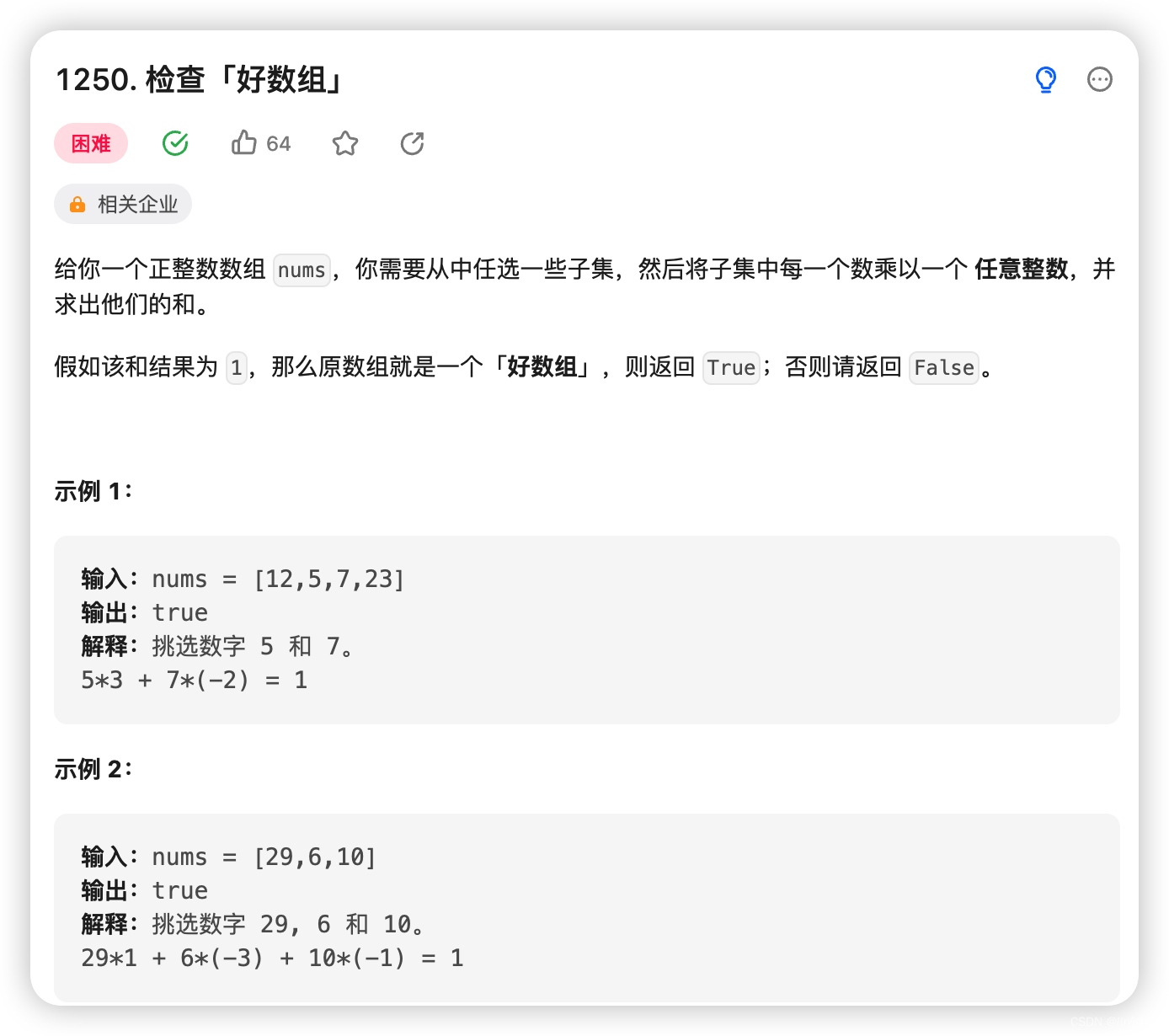
题目链接:https://leetcode.cn/problems/check-if-it-is-a-good-array/description/
思路
方法:数论
题目意思很简单,让你在数组 nums中选取一些子集,可以不连续,子集中的每个数再乘以任意的数的和是否为1,是则原数组就是个「好数组」
关键词:每个数相乘任意一个数相加,数论里「裴蜀定理」是一个关于最大公约数的定理。也是拥有类似的推导(具体证明可参考「裴蜀定理」OI Wiki)。
「裴(pei)蜀定理」:设 a,b 是不全为零的整数,则存在整数 x,y, 使得 ax+by= gcd(a,b).
「裴蜀定理」同样也可以推广到多个整数的情况。对于全不为 0 的任意 n 个整数 a1, a2, a3, a4 … an,记这 n 个整数的最大公约数为 0,则对于任意 n 个整数 x1, x2, x3, x4 … xn都满足 ∑i=1nai∗xi\sum_{i=1}^{n} a_i * x_i∑i=1nai∗xi 是 g 的倍数。
推论:正整数 a1 到 an 的最大公约数是 1 的充分必要条件是存在 n 个整数 x1 到 xn 满足 ∑i=1nai∗xi=1\sum_{i=1}^{n} a_i * x_i = 1∑i=1nai∗xi=1
回到原题,我们判断数组 nums 是否是个「好数组」。由「裴蜀定理」推导 0 < i < n,题目等价于求 nums 中的全部数字的最大公约数是否等于 1,若等于 1 则原数组为「好数组」,否则不是。
如何求数组 nums 的 最大公约数 g,初始化 g = nums[0],遍历数组,更新 g = gcd(g, nums[i]),遍历完全部数字后,g 即为数组 nums 中全部的元素的最大公约数。然后判断其是否等于 1 即可。在实现过程中我们也可以进一步做优化:如果遍历过程中出现最大公约数等于 1 的情况,则由于 1 和任何正整数的最大公约数都是 1,此时可以提前结束遍历。
代码示例
func isGoodArray(nums []int) bool {// 有数据为[1]的情况if len(nums) == 1 && nums[0] == 1{return true}g := nums[0]for i := 1; i < len(nums); i++ {g = gcd(g, nums[i])if g == 1 {return true}}return false
}func gcd(a, b int) int {if a % b == 0 {return b}return gcd(b, a % b)
}
复杂度分析
- 时间复杂度:O(n + logm\log mlogm),其中n表示数组 nums 长度,m 表示与最大公约数 g 迭代次数最长的数字,其中求单次最大公约数的时间复杂度为 O(logm\log mlogm),两个数求最大公约数,其中最大公约数 g 自增不减,总的求最大公约数所需时间为O(logm\log mlogm),所以总的所需时间O(n + logm\log mlogm)
- 空间复杂度:O(1),不需要额外申请空间
相关文章:

Leetcode-每日一题1250. 检查「好数组」(裴蜀定理)
题目链接:https://leetcode.cn/problems/check-if-it-is-a-good-array/description/ 思路 方法:数论 题目意思很简单,让你在数组 nums中选取一些子集,可以不连续,子集中的每个数再乘以任意的数的和是否为1ÿ…...
OpenStack手动分布式部署环境准备【Queens版】
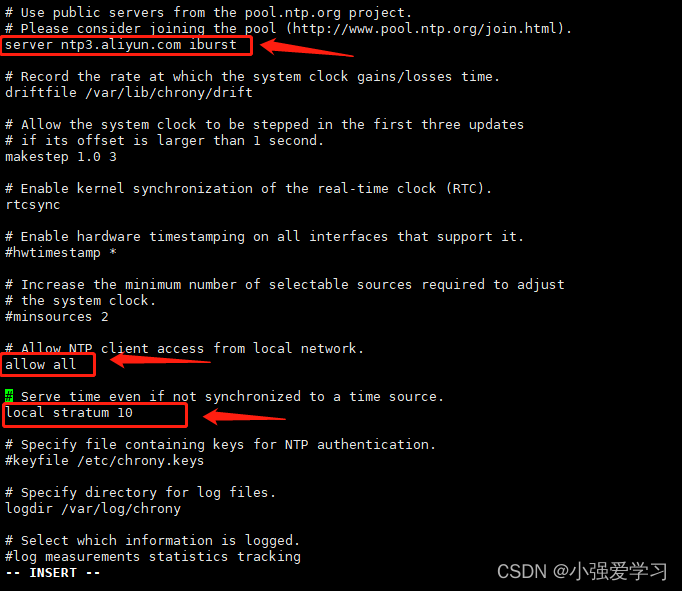
目录 1.基础环境准备(两个节点都需要部署) 1.1关闭防火墙 1.2关闭selinux 1.3修改主机名 1.4安装ntp时间服务器 1.5修改域名解析 1.6添加yum源 2.数据库安装配置 2.1安装数据库 2.2修改数据库 2.3重启数据库 2.4初始化数据库 3.安装RabbitMq…...

Web自动化测试——selenium的使用
⭐️前言⭐️ 本篇文章就进入了自动化测试的章节了,如果作为一名测试开发人员,非常需要掌握自动化测试的能力,因为它不仅能减少人力的消耗,还能提升测试的效率。 🍉欢迎点赞 👍 收藏 ⭐留言评论 …...

虚拟交换单元技术
支持VSU(Virtual Switch Unit)即虚拟交换单元技术。通过聚合链路连接,将多台物理设备虚拟为一台逻辑上统一的设备,使其能够实现统一的运行,利用单一IP 地址、单一Telnet 进程、单一命令行接口(CLI)、自动版本检查、自动…...
【STM32笔记】HAL库外部定时器、系统定时器阻塞、非阻塞延时
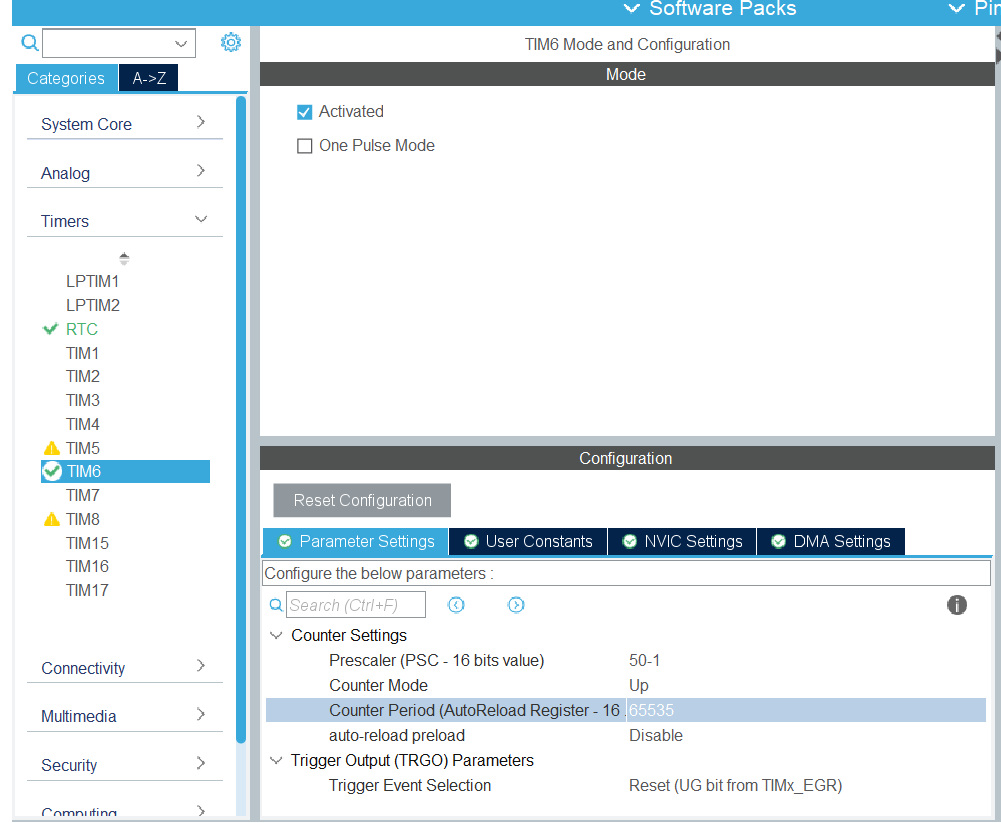
【STM32笔记】HAL库外部定时器、系统定时器阻塞、非阻塞延时 外部定时器 采用定时器做延时使用时 需要计算好分频和计数 另外还要配置为不进行自动重载 对于50MHz的工作频率 分频为50-1也就是50M/501M 一次计数为1us 分频为50000-1也就是1k 一次计数为1ms 我配置的是TIM6 只…...

[Springboot 单元测试笔记] - Mock 和 spy的使用
Springboot单元测试 - 依赖类mock测试 通常单元测试中,我们会隔离依赖对于测试类的影响,也就是假设所有依赖的一定会输出理想结果,在测试中可以通过Mock方法来确保输出结果,这也就引入另一个测试框架Mockito。 Mockito框架的作用…...

互联网新时代要来了(二)什么是AIGC?
什么是AIGC? 最近,又火了一个词“**AIGC”**2022年被称为是AIGC元年。那么我们敬请期待,AIGC为我们迎接人工智能的下一个时代。 TIPS:内容来自百度百科、知乎、腾讯、《AIGC白皮书》等网页 什么是AIGC?1.什么是AIGC?…...

75V的TVS二极管有哪些型号?常用的
瞬态抑制TVS二极管工作峰值反向电压最低3.3V,最高可达513V,甚至更高。很多电子工程师都知道,TVS二极管在实际应用选型过程中,第一步要确认的就是其工作峰值反向电压。2023年春节已过,东沃电子正月初八就开工了…...

测试开发之Django实战示例 第十章 创建在线教育平台
第十章 创建在线教育平台在上一章,我们为电商网站项目添加了国际化功能,还创建了优惠码和商品推荐系统。在本章,会建立一个新的项目:一个在线教育平台,并创内容管理系统CMS(Content Management System&…...
Hadoop高可用搭建(二)
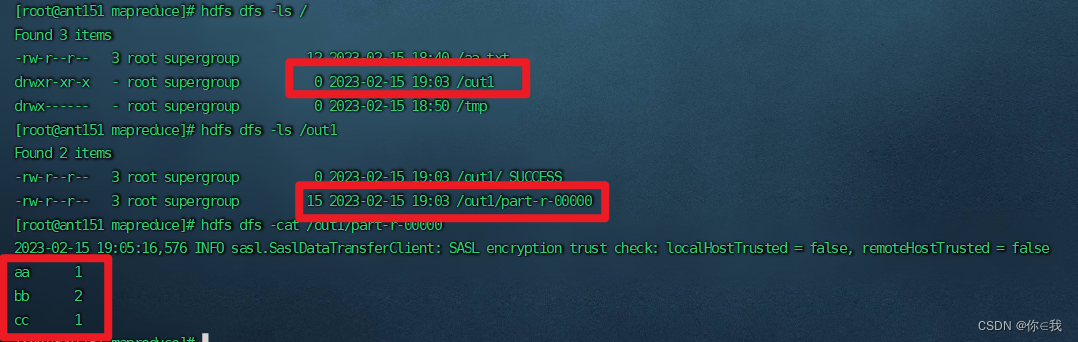
目录 解压Hadoop 改名 更改配置文件 workers hdfs-site.xml core-site.xml hadoop-env.sh mapred-site.xml yarn-site.xml 设置环境变量 启动集群 启动zk集群 启动journalnode服务 格式化hfds namenode 启动namenode 同步namenode信息 查看namenode节点状态 …...

如何用企微SCRM管理系统发掘老客户的新增长点?
如何用企微SCRM管理系统发掘老客户的新增长点? 一直做投放拉新,很快营销成本会难以支撑,如果在私域运营中始终留不下老用户,那么运营也是失败的。 开发老客户的成本只需新客户成本的1/6,但很多企业对老客户都忽视了&…...

我用python疯狂爬取公司数据
我是半路从一个纯小白学过来的,学习途中也掉过许多坑,在这里建议新手要先把基础打扎实,然后再去学习自己需要的内容,不要想着全部学完再用,那样你是永远学不完的,用哪方面就学习哪方面的内容,不…...

EMR集群运行TPC-DS在云盘和OSS中的对比
1.简介 TPC-DS是大数据领域最为知名的Benchmark标准。本文介绍使用阿里云EMR集群运行TPC-DS在云盘和OSS中的表现对比。 2.环境准备 1.创建EEMR-5.10.1集群 1个master,2个core,3台机器都s是4c16g。 2.安装Git和Maven sudo yum install -y git maven3.下载TPC-DS Benchmark工…...
菜鸟在 windows 下 python 中安装 jupyter 踩坑要点 、被神化的 VsCode
我平时用不到 python ,更没用过 jupyter ,因此我的 python知识仅限于知道有 python 这么个编程语言,会写个 print("Hello World!!!") 而已,完全没听过 jupyter ,因为某些原因今天需要安装下 jupyter 看看&am…...

k8s简单搭建
前言 最近学习k8s,跟着网上各种教程搭建了简单的版本,一个master节点,两个node节点,这里记录下防止以后忘记。 具体步骤 准备环境 用Oracle VM VirtualBox虚拟机软件安装3台虚拟机,一台master节点,两台…...

计算机SCI期刊审稿人,一般关注论文的那些问题? - 易智编译EaseEditing
编辑主要关心: (1)文章内容是否具有足够的创新性? (2)文章主题是否符合期刊的受众读者? (3)文章方法学是否合理,数据处理是否充分? (…...

Docker迁移以及环境变量问题
问题一描述将docker容器通过docker export命令打包,传输到另外的服务器,再通过docker import命令导入后,发现原来docker容器中的环境变量失效了。解决方案1. 【无效方案】直接在docker容器中通过export命令设置环境变量。export LD_LIBRARY_P…...
Sphinx文档生成工具(二)
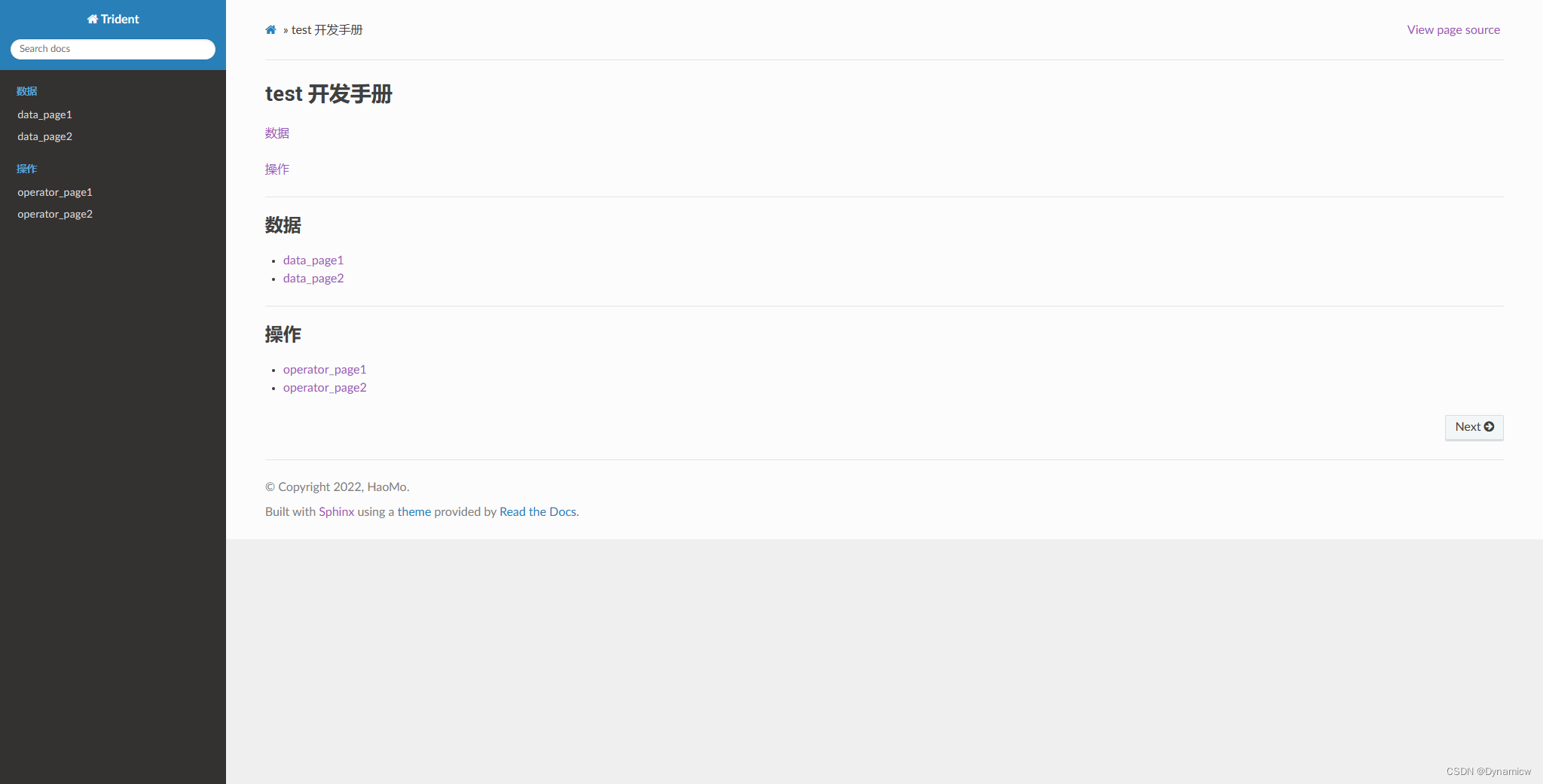
rst语法 官方的语法手册 行内的样式: #斜体 *message* #粗体 **message** #等宽 不能有换行 message标题 一级标题 ^^^^^^^^ 二级标题 --------- 三级标题 >>>>>>>>> 四级标题 ::::::::: 五级标题六级标题 """"…...

Python快速上手系列--JSON--入门篇
本章我们来看看json的一些应用。简单易懂还实用。一起来看看数据类型以及一些语法规则吧1、数字(整数或浮点数) 如:{"age":18, "score":70.5} 注意,数字直接写,不需要带任何符号2、字符串…...
axios中的GET POST PUT PATCH,发送请求时params和data的区别
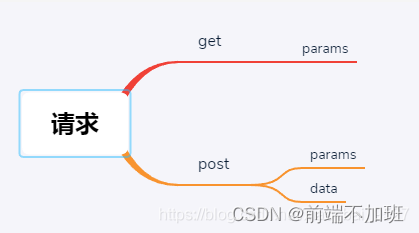
axios 中 get/post请求方式 1. 前言 最近突然发现post请求可以使用params方式传值,然后想总结一下其中的用法。 2.1 分类 经过查阅资料,get请求是可以通过body传输数据的,但是许多工具类并不支持此功能。 在postman中,选择get请…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
