HTTPS协议原理---详解
目录
一、HTTPS
1.加密与解密
2.我们为什么要加密?
3.常见加密方式
①对称加密
②非对称加密
4.数据摘要
5.数字签名
二、HTTPS的加密方案
1.只是用对称加密
2.只使用非对称加密
3.双方都使用非对称加密
4.非对称加密+对称加密
中间人攻击
证书
CA认证
理解数据签名
5.非对称加密+对称加密+证书认证
完整流程
查看浏览器所信任的证书发布机构
中间人有没有可能篡改该证书?
中间人是否可以掉包整个证书呢?
如何成为中间人?
总结:
一、HTTPS
上一篇博客,详细讲述了HTTP协议(超文本传输协议)的一些细节,在最后我们提到,无论如何HTTP 协议内容都是按照⽂本的⽅式明⽂传输的,这就导致在传输过程中出现⼀些被篡改的情况,所以当今的网站都是用的是HTTPS 协议,HTTPS 也是⼀个应⽤层协议. 是在 HTTP 协议的基础上引⼊了⼀个加密层。
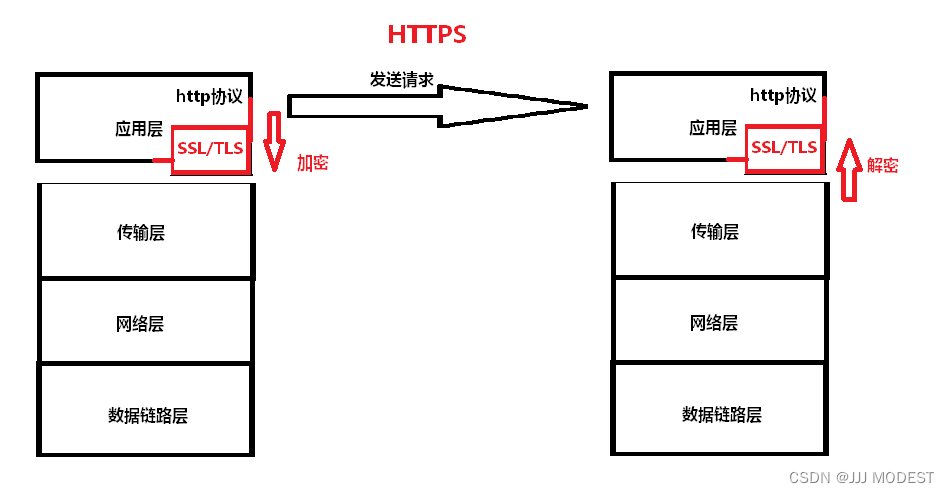
1.加密与解密
什么是加密?就是将明文转换为密文。
什么是解密?就是将密文转换为明文。
在这两个过程中,通常要密钥来辅佐。密钥是一种参数,它是在明文转换为密文或将密文转换为明文的算法中输入的参数。
例子:



通过密钥我们可以将密文转换为明文,反之亦然。
2.我们为什么要加密?
我们都会经历过这样一个现象。明明下载的是我们想要的软件,却弹出另一个软件的下载。
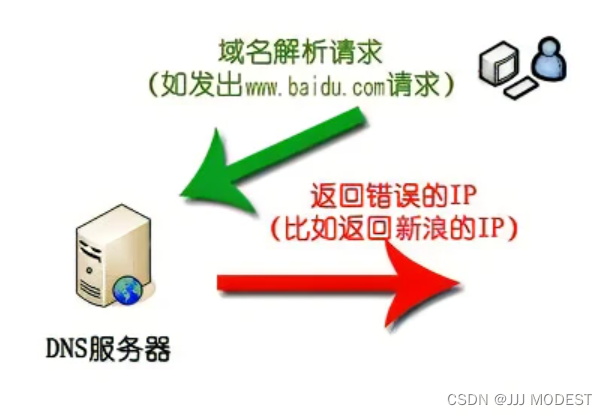
这就是臭名昭著的运营商的劫持。关于运营商劫持,我们要到后面才会讲到。
如图,我们发送HTTP请求,运营商接收到这个请求之后,发现请求为www.baidu.com,运营商就会将HTTP响应替换为新浪的官网。
因为http的内容是明⽂传输的,明⽂数据会经过路由器、wifi热点、通信服务运营商、代理服务 器等多个物理节点,如果信息在传输过程中被劫持,传输的内容就完全暴露了。劫持者还可以篡改传 输的信息且不被双⽅察觉,这就是中间人攻击 ,所以我们才需要对信息进⾏加密。
所以针对防止中间人攻击,我们要对数据进行加密,下文会讲述到“道与魔之间的对抗”,我们呢拼尽全力抵抗数据被截取,中间人总用方法来获取信息。可谓“道高一丈魔高一尺”。
3.常见加密方式
①对称加密
采⽤单钥密码系统的加密⽅法,同⼀个密钥可以同时⽤作信息的加密和解密,这种加密⽅法称为对称加密,也称为单密钥加密,特征:加密和解密所⽤的密钥是相同的。
常⻅对称加密算法:DES、3DES、AES、TDEA、Blowfish、RC2等
特点:算法公开、计算量⼩、加密速度快、加密效率⾼
例如:
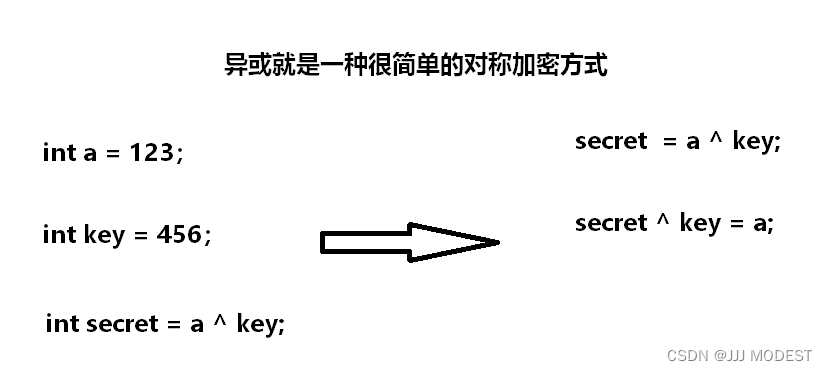
②非对称加密
需要两个密钥来进⾏加密和解密,这两个密钥是公开密钥(public key,简称公钥)和私有密钥 (private key,简称私钥)。
常⻅非对称加密算法(了解):RSA,DSA,ECDSA
特点:算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,⽽使得加密解密速度没有对 称加密解密的速度快。
非对称加密要⽤到两个密钥, ⼀个叫做 "公钥", ⼀个叫做 "私钥". 公钥和私钥是配对的. 最⼤的缺点就是运算速度⾮常慢,⽐对称加密要慢很多.
通过公钥对明⽂加密, 变成密⽂
通过私钥对密⽂解密, 变成明⽂
或者
通过私钥对明⽂加密, 变成密⽂
通过公钥对密⽂解密, 变成明⽂
4.数据摘要
数据摘要(数据指纹)这是通过利用单向散列函数(Hash函数)对信息进行运算,生成一段固定长度的数据摘要。
摘要常见算法:有MD5、SHA1、SHA256、SHA512等。
摘要特征:和加密算法的区别是,摘要严格意义不是加密,因为没有解密,只不过从摘要很难反推 原信息,通常⽤来进⾏数据对⽐。
这个摘要就像这个资源的身份证号一样,相同的几率微乎其微,我们可以通过数据摘要来比对判断不同资源是否相同。因为更改一个标点符号就会导致前后数据摘要不一样。
例如:当我上传电影时,会发现这个资源有时会瞬间就会被告知上传成功,但是有时需要很长时间几兆几兆的上传。只是因为,上传的软件会将电影等资源利用单向散列函数形成数据摘要,将数据摘要与服务器中的资源的数据摘要进行对比,如若有数据摘要与当前上传的文件的数据摘要相同,就证明服务器中有我们上传的这份资源,此时就不需要我们上传了,所以会被告知上传完毕。
注意,不可能通过数据摘要反向推出资源来,因为是使用单向散列函数来运算的。
5.数字签名
数字摘要通过加密就得到了数字签名。
二、HTTPS的加密方案
1.只是用对称加密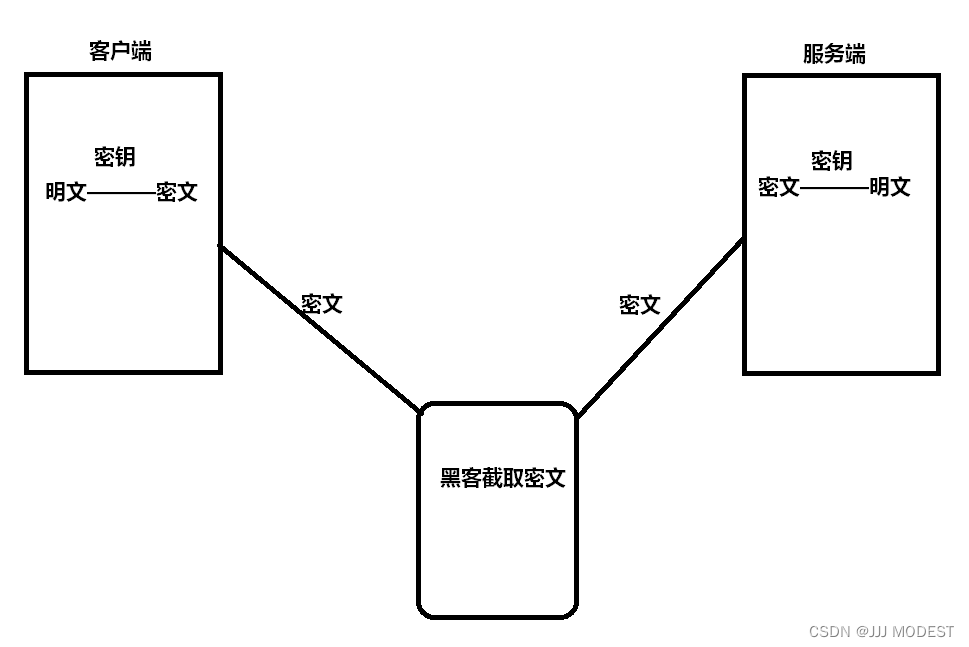
哇,这样不错诶,黑客(中间人)拿到的只是密文,看不到我的明文内容,这样多安全。
但事情绝没有这么简单,服务端同时给很多客户端提供服务,它们的密钥之间必是不同的,如果是相同的,就容易扩散,黑客很容易拿到。所以密钥之间是不同的。所以,需要服务端来维护每个客户端和服务端之间的密钥关系,也是一个麻烦的工程。
较为理想的情况为,在每次服务端和客户端建立关系之前就协商好密钥是什么。
但是,这个密钥在网络传输(协商)中是不是也要加密啊,不加密又要被黑客获取,但是加密又要使用密钥,这就是“先有鸡还是先有蛋”的问题了,所以这个方法行不通。
2.只使用非对称加密 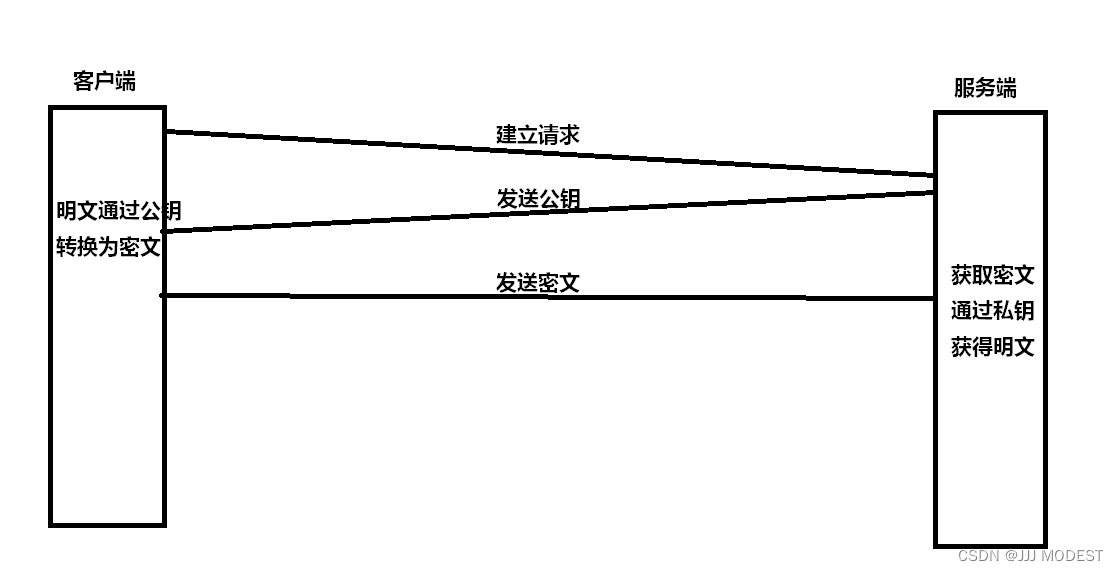
这样很是不错,因为中间人只能获得我的公钥和密文,但是获得不了私钥,所以解密不了,但是,这有很大隐患,只能由客户端发信息,而不能由服务端发信息。
因为客户端只有公钥,所以服务端只能用私钥加密,发送信息 ,这时中间人截取信息,通过先前截取的公钥就可以获得信息。那如果服务端通过公钥加密,那客户端没有私钥就不能解密。
只使用非对称加密是行不通的。
3.双方都使用非对称加密
上个方案只是客户端有公钥,服务端有私钥,保证单方面的保密可行。这一次客户端和服务端都具有独有的公钥与私钥,然后互换公钥。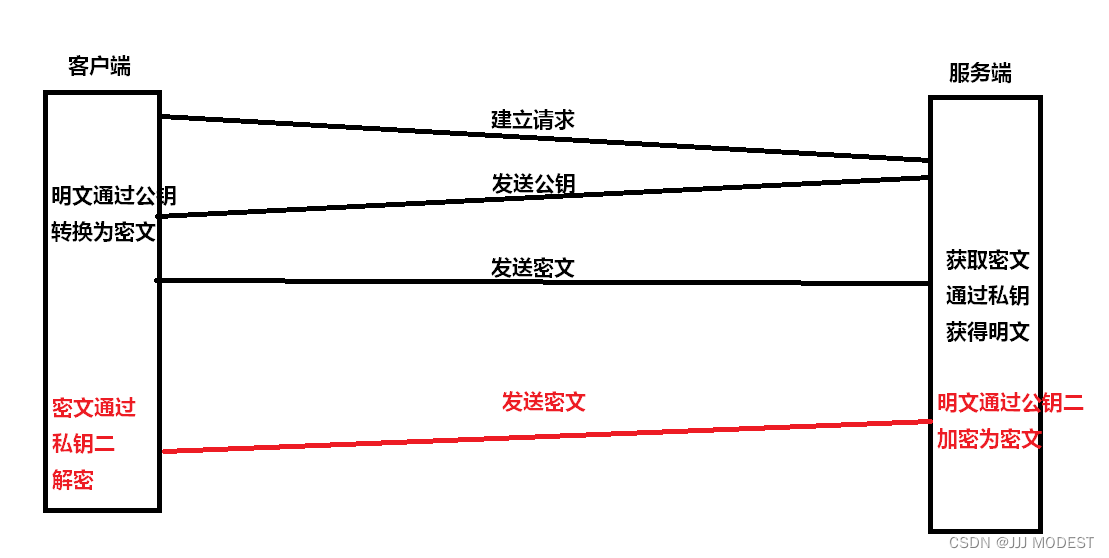
这种方法可行,但是非对称加密速度与对称加密相比慢得多,会产生效率问题,并且还会有安全问题。
4.非对称加密+对称加密
服务器具有非对称公钥1和私钥1。
客户端发起Http请求,获取公钥1。
客户端形成对称密钥2,通过公钥1,将对称密钥2发给服务端,中间人因为没有私钥1,所以获取之后解密不了,服务端获取密文通过私钥1解密之后获得对称密钥2.
之后客户端和服务端都使用对称密钥2来加密解密,快捷可靠。
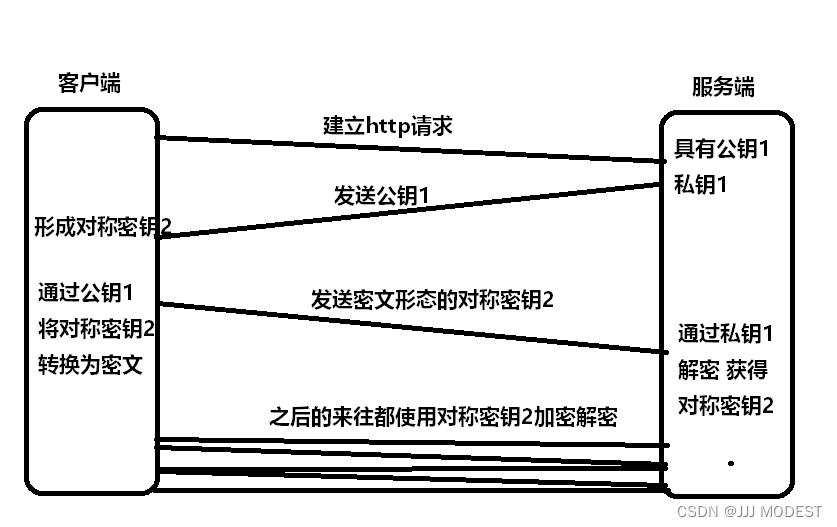
中间人攻击
这几个方案都逃不过中间人攻击这个手段。
我们以方案四作为底层方案,设想一下,如果在建立http请求的时候中间人,伪装成客户端和服务端,与不同的双方交流都伪装成对面的一端,这样方案四就漏洞百出,我们根据图示理解。
中间人干了这么多事情最主要的是假装自己对方通信的另一端,最终为了获取客户端的对称密钥,这样接下来的客户端和服务端之间的通信对中间人毫无秘密可言。
证书
CA认证
服务端在使⽤HTTPS前,需要向CA机构申领⼀份数字证书,数字证书⾥含有证书申请者信息、公钥信 息等。服务器把证书传输给浏览器,浏览器从证书⾥获取公钥就⾏了,证书就如⾝份证,证明服务端 公钥的权威性。
我们下一个方案需要证书的帮助。

理解数据签名
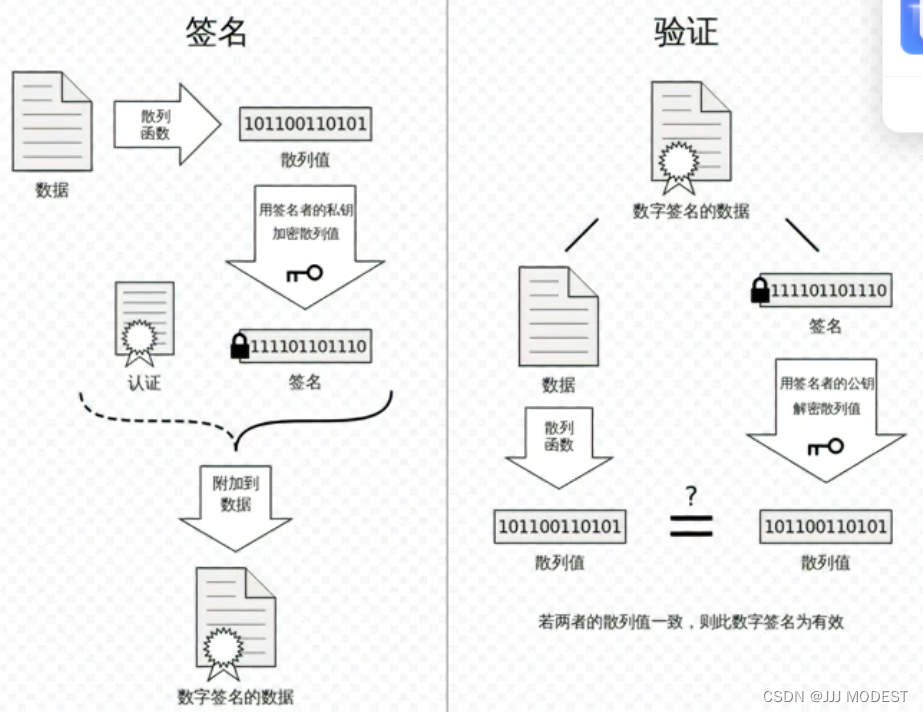
数据签名的目的是防止数据被篡改。
如果中间人拿到数字签名的数据,将其中的数据做修改,然后通过散列函数形成散列值,但是中间人没有签名者的私钥,不能将散列值转换为签名(即无法将更改之后的数据转换为签名,即使使用自己的私钥加密之后将签名更换,之后的还需要有签名者的公钥来解密,就会原形毕露),最后再验证的时候原有的签名经过签名者的公钥得出的散列值和已经被篡改的数据形成的散列值不一致,这个数字签名就没有用了。
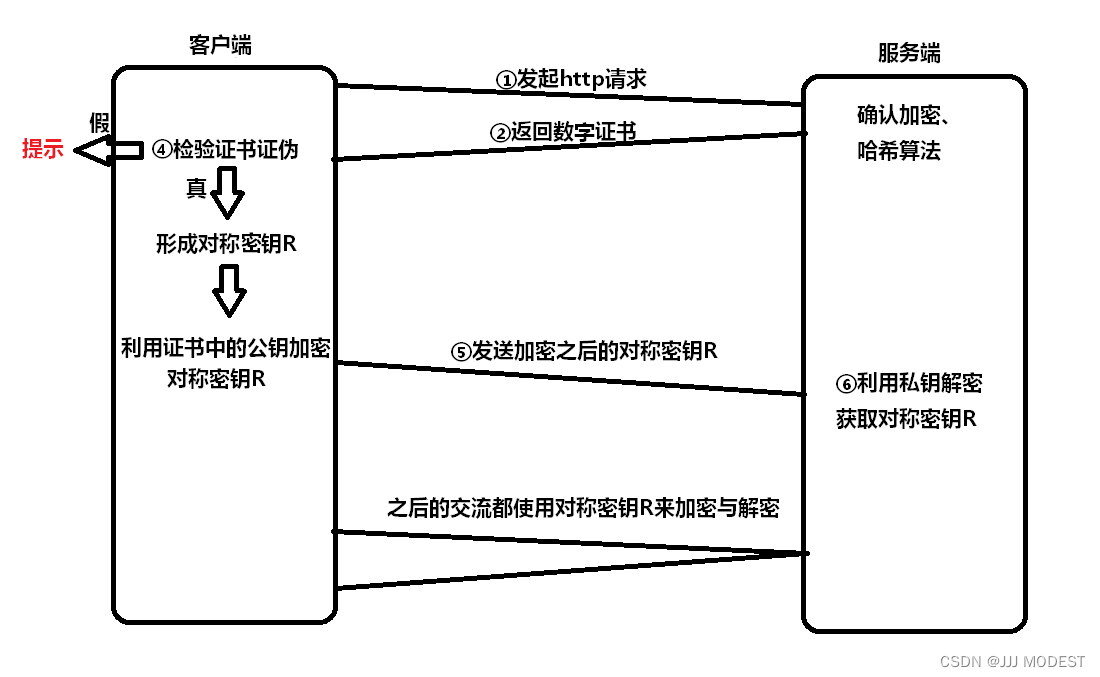
5.非对称加密+对称加密+证书认证
在客户端和服务器刚⼀建⽴连接的时候, 服务器给客户端返回⼀个证书,证书包含了之前服务端的公钥, 也包含了⽹站的⾝份信息。
当客户端获取证书后,会检查证书的证伪。
判断证书的有效期是否过期。
判断发布证书的机构是否受信任。
验证证书是否被篡改。从系统中拿到发布证书的机构的公钥,将签名解密,得到hash1(数据摘要),再将数据(证书)通过散列函数得到hash2,比对hash1与hash2的值,相同则为该证书未被篡改过。
完整流程
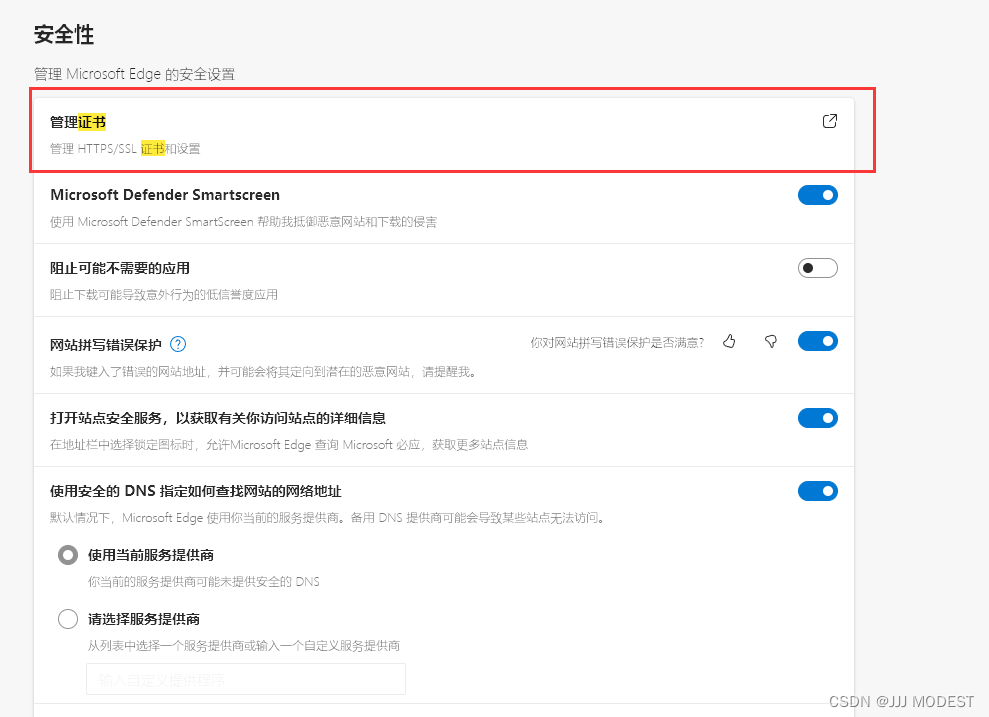
查看浏览器所信任的证书发布机构
在edge浏览器中,此处就可以查看
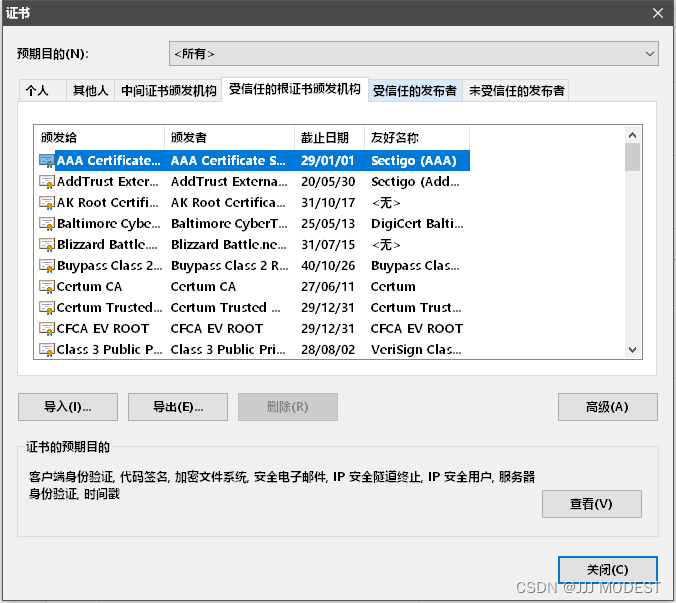
我们点开一个证书查看细节。
我们会发现他们包含了我们所说的关键信息。

中间人有没有可能篡改该证书?
先前我们说过,这里在简洁的表述。
中间人篡改证书,将原文修改,但是他没有CA机构的私钥,无法将更改的数据经过hash再通过私钥转形成签名。如果强⾏篡改,客⼾端收到该证书后会发现明⽂和签名解密后的值不⼀致,则说明证书已被篡改, 证书不可信,从⽽终⽌向服务器传输信息,防⽌信息泄露给中间⼈。
中间人是否可以掉包整个证书呢?
我们要知道,客户端在认证时都是通过认证机构的公钥来检查证书的真伪的,所以中间人没有响应的私钥就是不可行的,转而去申请真的证书,然后用自己的证书将客户端接受的证书进行调换。
方法是可行的,但是证书明⽂中包含了域名等服务端认证信息,如果整体掉包,客户端依旧能够识别出来。
如何成为中间人?
ARP欺骗:在局域⽹中,hacker经过收到ARP Request⼴播包,能够偷听到其它节点的 (IP, MAC) 地址。例, ⿊客收到两个主机A, B的地址,告诉B (受害者) ,⾃⼰是A,使得B在发送给A 的数据包 都被⿊客截取。
ICMP攻击:由于ICMP协议中有重定向的报⽂类型,那么我们就可以伪造⼀个ICMP信息然后发送给 局域⽹中的客⼾端,并伪装⾃⼰是⼀个更好的路由通路。从⽽导致⽬标所有的上⽹流量都会发送到 我们指定的接⼝上,达到和ARP欺骗同样的效果。
总结:
第一组非对称密钥,CA机构拥有的私钥,客户端拥有公钥,这两个密钥合作起来,来检查证书的真伪。
第二组非对称密钥,客户端生成对称密钥,通过公钥,将对称密钥加密,发回给服务端,服务端通过私钥解密,获得对称密钥。
第三组对称密钥,客户端和服务器后续传输的数据都通过这个对称密钥加密解密。
感谢观看,如有错误请指出,我们下次再见。
相关文章:

HTTPS协议原理---详解
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
Pytest学习笔记
Pytest学习笔记 1、介绍 1.1、单元测试 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试 1.2、单元测试框架 测试发现:从多个py文件里面去找到我们测试用例测试执行:按…...
Fuzz概述
文章目录AFL一些概念插桩与覆盖率边和块覆盖率afl自实现劫持汇编器clang内置覆盖率反馈与引导变异遗传算法fork server机制AFL调试准备AFL一些概念 插桩与覆盖率 边和块 首先,要明白边和块的定义 正方形的就是块,箭头表示边,边表示程序执行…...
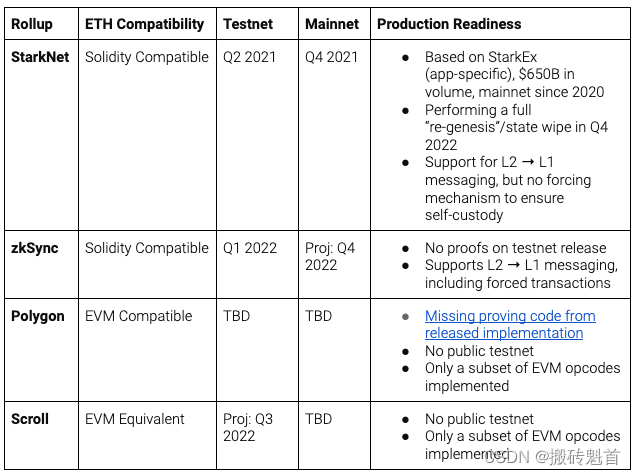
区块链知识系列 - 系统学习EVM(四)-zkEVM
区块链知识系列 - 系统学习EVM(一) 区块链知识系列 - 系统学习EVM(二) 区块链知识系列 - 系统学习EVM(三) 今天我们来聊聊 zkEVM、EVM 兼容性 和 Rollup 是什么? 1. 什么是 Rollup rollup顾名思义,就是把一堆交易卷(rollup)起来…...

Leetcode.2341 数组能形成多少数对
题目链接 Leetcode.2341 数组能形成多少数对 Rating : 1185 题目描述 给你一个下标从 0 开始的整数数组 nums。在一步操作中,你可以执行以下步骤: 从 nums选出 两个 相等的 整数从 nums中移除这两个整数,形成一个 数对 请你在 nums上多次执…...

C++复习笔记10
1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一个元素。 3. list与for…...
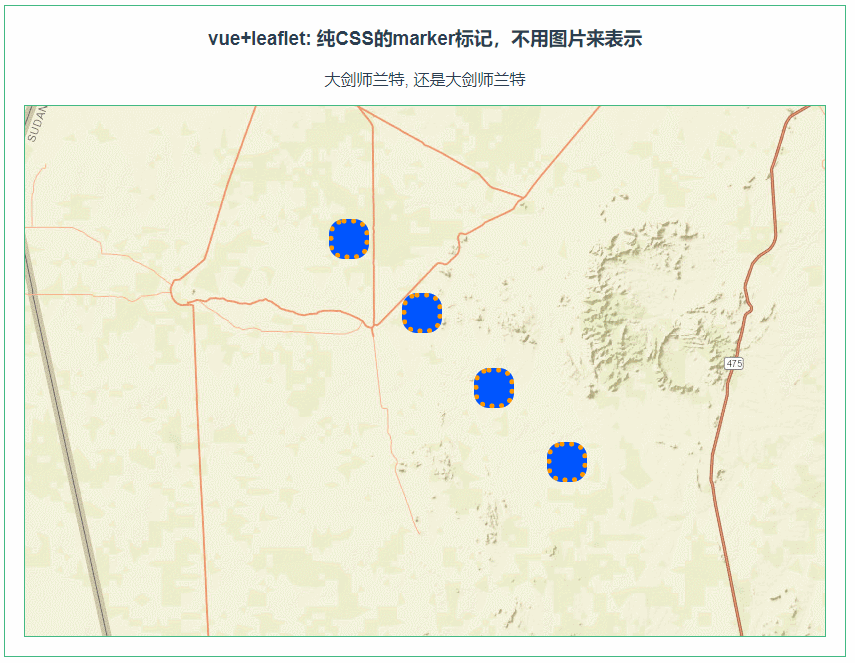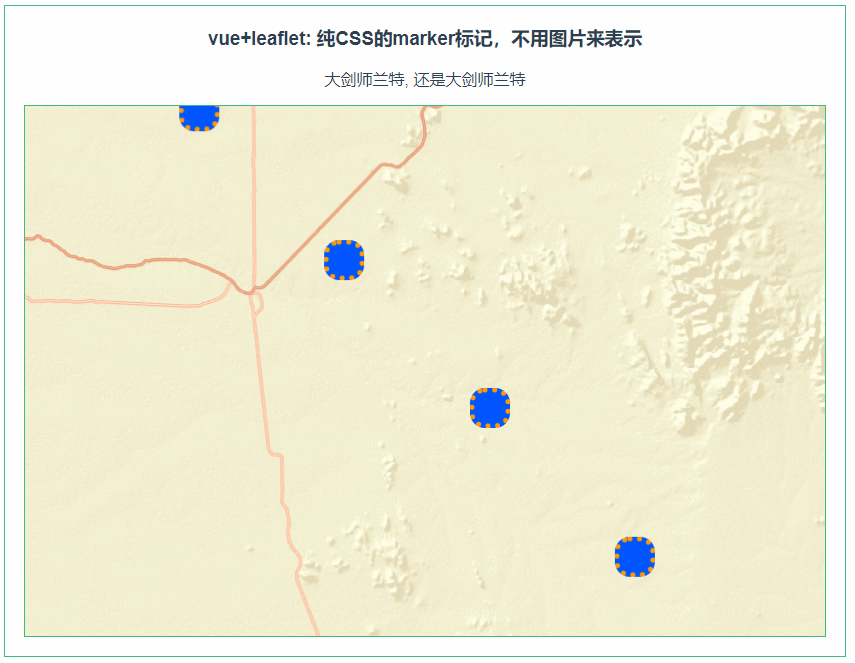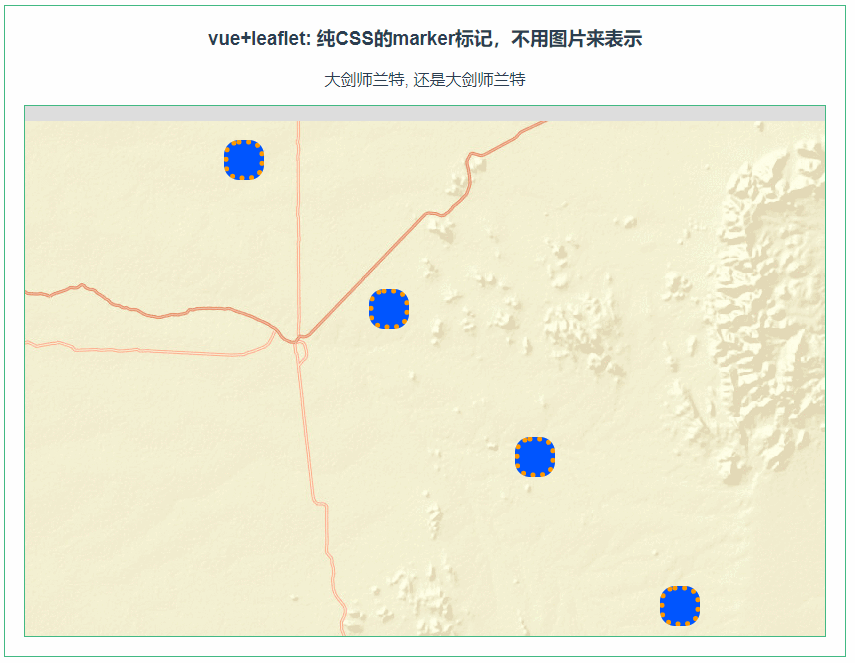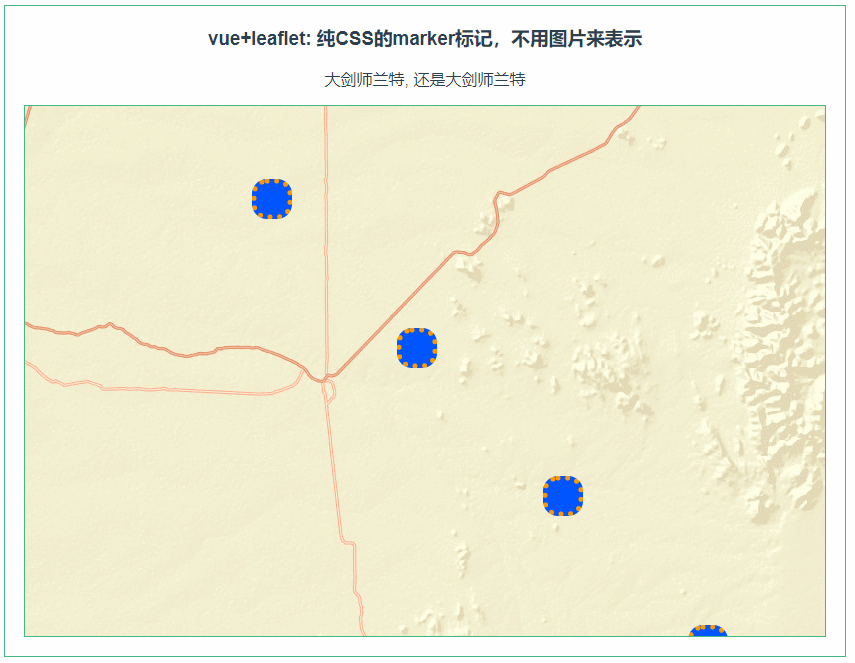
leaflet 纯CSS的marker标记,不用图片来表示(072)
第072个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用纯CSS来打造marker的标记。这里用到的是L.divIcon来引用CSS来构造新icon,然后在marker的属性中引用。 这里必须要注意的是css需要是全局性质的,不能被scoped转义为其他随机的css。 直接复制下面的 v…...
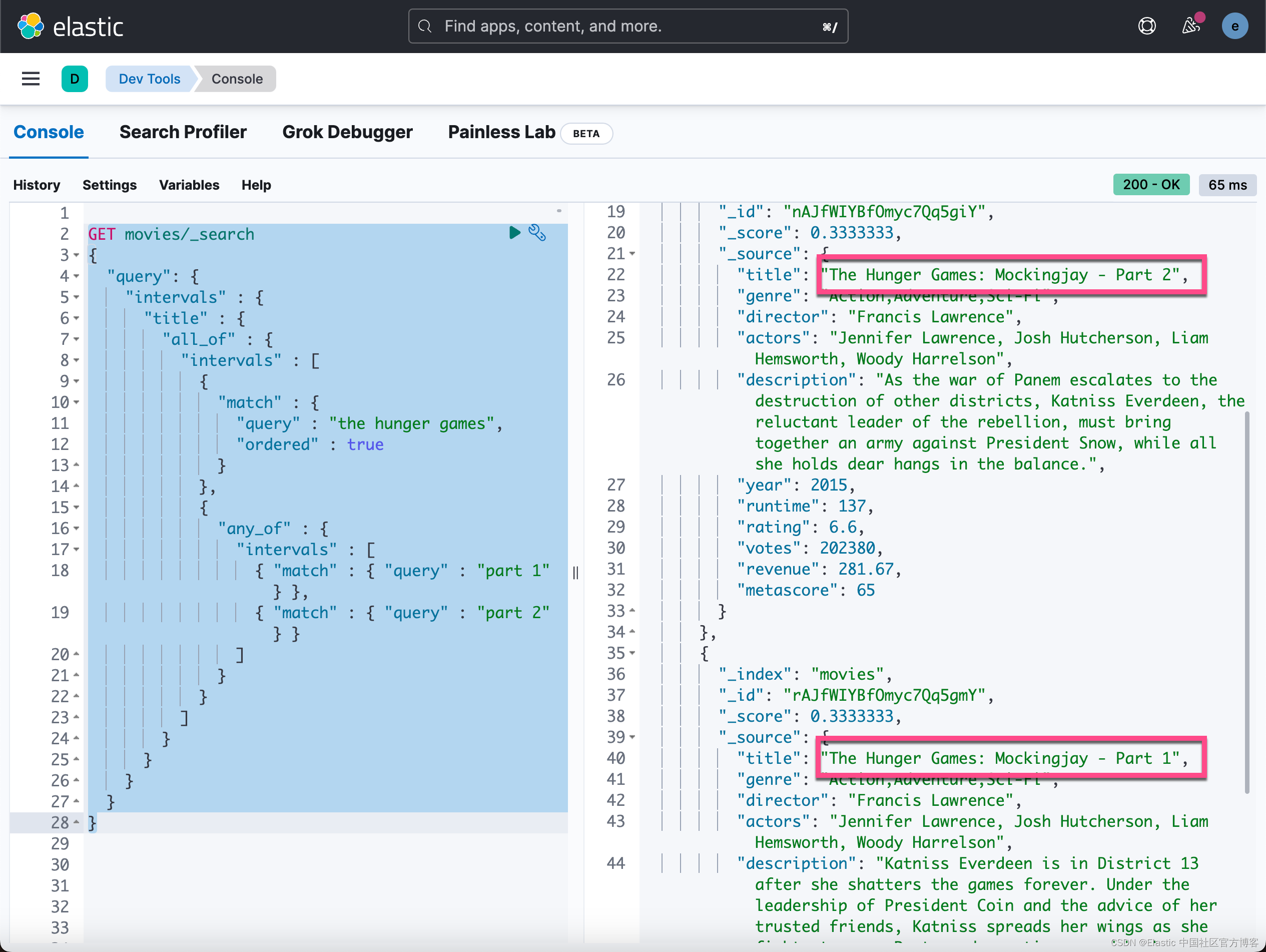
Elasticsearch:使用 intervals query - 根据匹配项的顺序和接近度返回文档
Intervals query 根据匹配项的顺序和接近度返回文档。Intervals 查询使用匹配规则,由一小组定义构成。 然后将这些规则应用于指定字段中的术语。 这些定义产生跨越文本正文中的术语的最小间隔序列。 这些间隔可以通过父源进一步组合和过滤。 上述描述有点费解。我…...
无法决定博客主题的人必看!如何选择类型和推荐的 5 种选择
是否有人不能迈出第一步,因为博客的类型还没有决定?有些人在出发时应该行动,而不是思考,但让我们冷静下来,仔细想想。博客的难度因流派而异,这在很大程度上决定了随后的发展。因此,在选择博客流…...
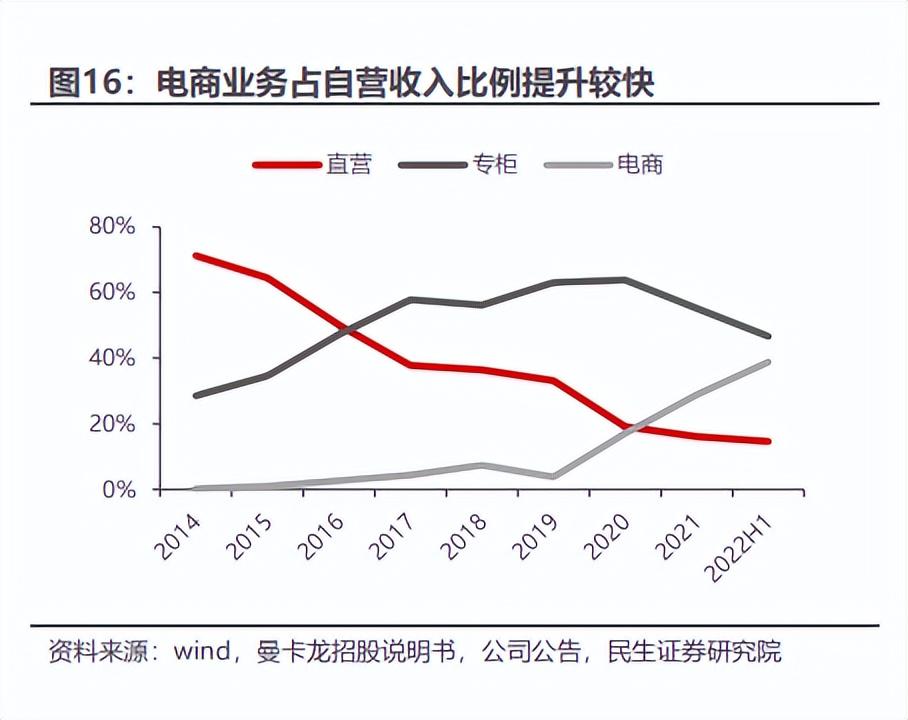
数字化转型的成功模版,珠宝龙头曼卡龙做对了什么?
2月11日,曼卡龙(300945.SZ)发布2022年业绩快报,报告期内,公司实现营业收入16.11亿元,同比增长28.63%。来源:曼卡龙2022年度业绩快报曼卡龙能在2022年实现营收增长尤为不易。2022年受疫情影响&am…...
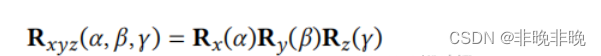
转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录1. 转换矩阵、平移矩阵、旋转矩阵之间的关系2. 缩放变换、平移变换和旋转变换2. python实现旋转矩阵、四元数、欧拉角互相转化由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄…...
中国地图航线图(echarjs)
1、以上为效果图 需要jq、echarjs、china.json三个文件支持。以上 2、具体代码 DOM部分 <!-- 服务范围 GO--> <div class"m-maps"><div id"main" style"width:1400px;height: 800px; margin: 0 auto;"> </div> <!-…...
Python正则表达式中group与groups的用法详解
本文主要介绍了Python正则表达式中group与groups的用法详解,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧目录在Python中,正则表达式的group和groups方…...

c++练习题7
1.下列运算符中优先级最高的是 A)> B) C) && D)! 2.以下关于运算符优先级的描述中,正确的是 。 A)!(逻辑非&#x…...

MySQL学习
目录1、数据库定义基本语句(1)数据库操作(2)数据表操作2.数据库操作SQL语句(1)插入数据(2)更新语句(3)删除数据3.数据库查询语句(1)基…...

C语言(强制类型转换)
一.类型转换原则 1.升级:当类型转换出现在表达式时,无论时unsigned还是signed的char和short都会被自动转换成int,如有必要会被转换成unsigned int(如果short与int的大小相同,unsigned short就比int大。这种情况下,uns…...

搭建hadoop高可用集群(二)
搭建hadoop高可用集群(一)配置hadoophadoop-env.shworkerscore-site.xmlhdfs-site.xmlmapred-site.xmlyarn-site.xml/etc/profile拷贝集群首次启动1、先启动zk集群(自动化脚本)2、在hadoop151,hadoop152,hadoop153启动JournalNode…...

CentOS升级内核-- CentOS9 Stream/CentOS8 Stream/CentOS7
官方文档在此 升级原因 当我们安装一些软件(对,我说的就是Kubernetes),可能需要新内核的支持,而CentOS又比较保守,不太升级,所以需要我们手工升级. # 看下目前是什么版本内核 uname -a# 安装公钥 rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org# 添加仓库,如果…...
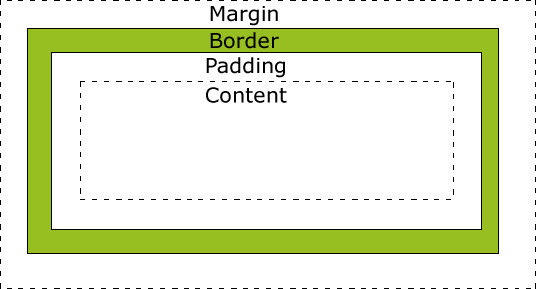
【基础篇】一文掌握css的盒子模型(margin、padding)
1、CSS 盒子模型(Box Model) 所有HTML元素可以看作盒子,在CSS中,"box model"这一术语是用来设计和布局时使用。CSS盒模型本质上是一个盒子,封装周围的HTML元素,它包括:边距,边框,填充,和实际内容。盒模型允许我们在其它元素和周围元素边框之间的空间放置元素…...
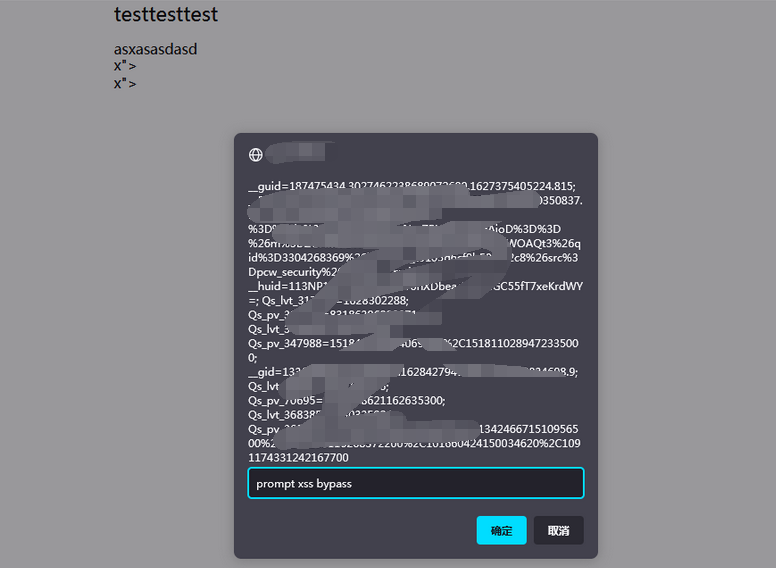
重生之我是赏金猎人-漏洞挖掘(十一)-某SRC储存XSS多次BypassWAF挖掘
0x01:利用编辑器的超链接组件导致存储XSS 鄙人太菜了,没啥高质量的洞呀,随便水一篇文章吧。 在月黑风高的夜晚,某骇客喊我起床挖洞,偷瞄了一下发现平台正好出活动了,想着小牛试刀吧 首先信息收集了一下&a…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
