Lesson 7.2 Mini Batch K-Means与DBSCAN密度聚类
文章目录
- 一、Mini Batch K-Means 算法原理与实现
- 二、DBSCAN 密度聚类基本原理与实践
- 1. K-Means 聚类算法的算法特性
- 2. DBSCAN 密度聚类基本原理
- 3. DBSCAN 密度聚类的 sklearn 实现
- 除了 K-Means 快速聚类意外,还有两种常用的聚类算法。
- (1) 是能够进一步提升快速聚类的速度的 Mini Batch K-Means 算法.
- (2) 则是能够和 K-Means 快速聚类形成性能上互补的算法 DBSCAN 密度聚类。
# 科学计算模块
import numpy as np
import pandas as pd
# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt
# 自定义模块
from ML_basic_function import *
# K-Means
from sklearn.cluster import KMeans
一、Mini Batch K-Means 算法原理与实现
- K-Means 算法作为最常用的聚类算法,在长期的使用过程中也诞生了非常多的变种,典型的如提高迭代稳定性的二分 K 均值法、能够显著提升算法执行速度的 Mini Batch K-Means。
- 由于聚类算法的稳定性可以通过 k-means++ 以及多次迭代选择最佳划分方式等方法解决,此处重点介绍 Mini Batch K-Means 算法。
- 顾名思义,所谓 Mini Batch K-Means 算法,就是在 K-Means 基础上增加了一个 Mini Batch 的抽样过程,并且每轮迭代中心点时,不在带入全部数据、而是带入抽样的 Mini Batch 进行计算。即每一轮的迭代操作更新为
- (1) 从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心;
- (2) 根据小批量数据划分情况,更新质心。
- 此处可以用梯度下降和小批量(Mini Batch)梯度下降之间的差异进行类比。
- 在梯度下降的过程中,我们带入全部数据构造损失函数,相当于带入全部数据进行参数的更新,就类似于 K-Means 带入每个簇的全部数据进行中心点位置计算。
- 而在小批量梯度下降的过程中,实际上我们是借助小批数据构造损失函数并对参数进行更新,就类似于 Mini Batch K-Means 中利用小批数据更新中心点。
- 而 Mini Batch K-Means 的有效性,其实也和小批量梯度下降的有效性类似,那就是对于一组规律连贯的数据集来说,小批量数据能够很大程度反映整体数据集规律,因此带入小批量数据进行计算是有效的。
- 此外,Mini Batch K-Means 相比 K-Means 的优劣势,也和小批量梯度下降对比梯度下降过程类似,采用小批数据带入进行计算能够极大缩短单次运算时间,因此迭代速度会更快,但由于小批量数据还是和整体数据之间存在差异,因此每次计算结果的精度不如带入整体数据的计算结果。
- 不过对于 K-Means 是否会落入局部最小值陷阱,我们可以通过 k-means++ 以及重复多次训练模型来解决,因此 Mini Batch K-Means 并不用承担跨越局部最小值陷阱的职责,所以 Mini Batch K-Means 对比 K-Means,其实就相当于牺牲了部分精度来换取聚类速度。
- 而聚类算法毕竟不是有监督学习算法,因此如果是面对海量数据的聚类,我们是可以考虑牺牲部分精度来换取聚类执行的速度的(当然这也要视情况而定)。
- 此处所谓小批量聚类精度不足,指的是小批量聚类和 K-Means 聚类结果上的差异,一般我们会认为 K-Means 聚类是精准的,而小批量聚类如果出现了和 K-Means 聚类不同的结果,则说明小批量聚类出现了误差,也就是精度不足。
- 接下来尝试调用相关评估器进行 Mini Batch K-Means 聚类:
from sklearn.cluster import MiniBatchKMeans
- 我们发现,MiniBatchKMeans 中部分参数和 K-Means 中参数不同,我们针对这些不同的参数来进行解释。
MiniBatchKMeans?
| Name | Description |
|---|---|
| batch_size | 小批量抽样的数据量 |
| compute_labels | 在聚类完成后,是否对所有样本进行类别计算 |
| max_no_improvement | 当SSE不发生变化时,质心最多再迭代多少次 |
| init_size | 用于生成初始中心点的样本数量 |
| reassignment_ratio | 某比例,数值越大、样本数越少的簇被重新计算中心点的概率就越大 |
- 能够发现,MiniBatchKMeans 在参数设置上和 K-Means 有两方面差异:
- (1) 是在迭代收敛条件上,通过查看说明文档我们不难发现,MiniBatchKMeans 主要通过 max_no_improvement 和 max_iter 两个参数来控制收敛,在默认情况下不采用 tol 参数。其根本原因在于小批量聚类往往需要迭代很多轮,因而出实际未收敛、但现两次相邻的迭代结果中 SSE 变化值小于 tol 的情况的概率会显著增加,因此此时我们不能以 tol 条件作为收敛条件;
- (2) 是在控制结果精度上,尽管小批量聚类是用精度换速度,但仍然提供了可以提升聚类精度的参数,也就是 reassignment_ratio,当发现聚类结果不尽如人意时,可以适当提升该参数的取值。
- 接下来,尝试调用相关评估器进行建模:
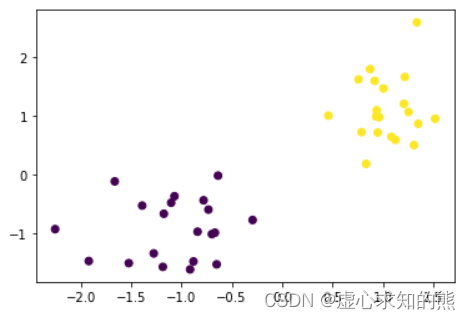
mbk = MiniBatchKMeans(n_clusters=2)np.random.seed(23)
X, y = arrayGenCla(num_examples = 20, num_inputs = 2, num_class = 2, deg_dispersion = [2, 0.5])plt.scatter(X[:, 0],X[:, 1],c=y)
mbk.fit(X)
#MiniBatchKMeans(n_clusters=2)# 观察聚类结果
plt.scatter(X[:, 0], X[:, 1], c=mbk.labels_)
plt.plot(mbk.cluster_centers_[0, 0], mbk.cluster_centers_[0, 1], 'o', c='red')
plt.plot(mbk.cluster_centers_[1, 0], mbk.cluster_centers_[1, 1], 'o', c='cyan')
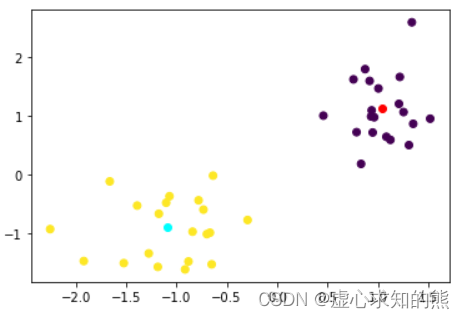
- 我们发现,在简单数据集的聚类过程中,MiniBatchKMeans 和 KMeans 并没有太大差异,接下来我们尝试在更大的数据集上来进行聚类,测试二者的精度和运算速度:
np.random.seed(23)
X, y = arrayGenCla(num_examples = 1000000, num_inputs = 10, num_class = 5, deg_dispersion = [4, 1])km = KMeans(n_clusters=5, max_iter=1000)
mbk = MiniBatchKMeans(n_clusters=5, max_iter=1000)# 导入时间模块
import time
# K-Means聚类用时
t0 = time.time()
km.fit(X)
t_batch = time.time() - t0
t_batch
#12.087070941925049# MiniBatchKMeans聚类用时
t0 = time.time()
mbk.fit(X)
t_batch = time.time() - t0
t_batch
#3.6028831005096436
- 能够发现,MiniBatchKMeans 聚类速度明显快于 K-Means 聚类,接下来查看二者 SSE 来对比其精度:
km.inertia_
#49994316.22276671mbk.inertia_
#50166895.159873486
- 能够发现,MiniBatchKMeans 精度略低于 K-Means,但整体结果相差不大,基本可忽略不计,当然这也是因为当前数据集分类性能较好的原因。
- 不过经此也可验证 MiniBatchKMeans 聚类的有效性。一般来说,对于 2 万条以上的数据集,MiniBatchKMeans 聚类的速度优势就会逐渐显现。
- 当然,如果希望更进一步提高迭代速度,可以适度减少 batch_size、减少 reassignment_ratio、max_no_improvement 这三个参数,不过代价就是聚类的精度可能会进一步降低,而如果希望提高精度,则可以提升 reassignment_ratio 参数,不过相应的,运行时间将会有所提升。
二、DBSCAN 密度聚类基本原理与实践
1. K-Means 聚类算法的算法特性
- 尽管 MiniBatchKMeans 能够有效提高聚类速度、提升聚类效率,但从最终聚类效果上来看,MiniBatchKMeans 和 K-Means 聚类算法仍然属于同一类聚类——假设簇的边界是凸形的聚类。
- 换而言之,就是这种聚类能够较好的捕捉圆形/球形边界(直线边界可以看成是大直径的圆形边界),而对于非规则类边界,则无法进行较好的聚类,当然这也是和 K-Means 聚类的核心目的:让更相近同一个中线点的数据属于一个簇,息息相关。
- 但有些时候,更接近同一个中心点的数据却不一定应该属于一个簇,例如如下情况:
from sklearn.datasets import make_moonsX, y = make_moons(200, noise=0.05, random_state=24)
plt.scatter(X[:,0], X[:,1], c = y)
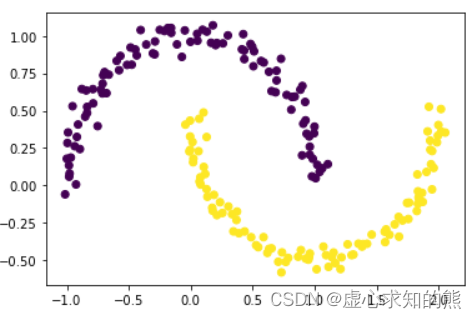
- 其中 make_moons 函数是 datasets 模块中创造数据集的函数,默认创建月牙形数据分布的数据集,并且 noise 参数取值越小、数据分布越贴近月牙形状。
- 当然此时我们发现,上述数据集明显可分为两个簇,但两个簇的边界却不是凸型的。此时如果我们用 K-Means 对其进行聚类,则会得到如下结果:
km = KMeans(n_clusters=2)
km.fit(X)
#KMeans(n_clusters=2)plt.scatter(X[:,0], X[:,1], c = km.labels_)
plt.plot(km.cluster_centers_[:,0], km.cluster_centers_[:,1], 'ro')
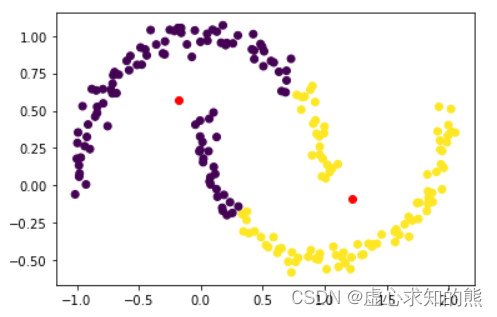
- 从上述结果中也能很明显的看出 K-Means 聚类的凸型边界,但很明显,此时聚类结果并不合理,上图中有多处彼此相邻但却不属于同一类的情况出现。
- 此时如果我们希望捕获上述非凸的边界,则需要使用一种基于密度的聚类方法,也就是我们将要介绍的 DBSCAN 密度聚类。
- 不过此处需要强调的是,尽管上述情况主观判断不太合理,但最终上述结果是否可用,还是需要结合实际业务进行考虑,这也是无监督学习算法没有统一的评价标准的具体表现。
- 此处我们只能说 K-Means 算法性能使得其无法捕获不规则边界,但这个特性导致的结果好坏无法直接通过数据结果进行得出。
2. DBSCAN 密度聚类基本原理
- 和 K-Means 依据中心点划分数据集的思路不同,DBSCAN 聚类则是试图通过寻找特征空间中点的分布密度较低的区域作为边界,并进一步以此划分数据集。
- 正是因为以低密度区域作为边界,DBSCAN 最终对数据的划分边界很有可能是不规则的,从而突破了 K-Means 依据中心点划分数据集从而使得边界是凸型的限制。
- 当然对于给予密度的聚类算法,最重要的是给出密度的相关的定义。在 DBSCAN 中,我们通过两个概念和密度密切相关:分别是半径(eps)与半径范围内点的个数(num_samples)。
- 对于数据集中任意一个点,只要给定一个 eps,就能算出对应的 num_samples,例如对于下述 A 点,在一个 eps 范围内,num_samples 为 7(包括自己)。
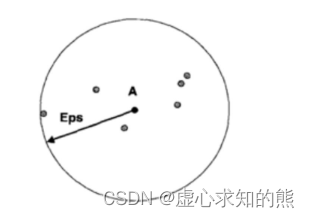
- 当然,eps 越小、num_samples 越大,则说明该点所在区域密度较高。
- 当然,我们可以据此设置一组参数,即半径(eps)和半径范围内至少包含多少点(min_samples)作为评估指标,来对数据集中不同的点进行密度层面的分类。
- 例如我们令 eps=Eps(某个数),min_samples=6,并且如果某点在一个 Eps 范围内包含的点的个数大于 min_samples,则称该点为核心点(core point),如下图中的 A 点。
- 而如果某个点不是核心点,但是在某个核心点的一个 eps 领域内,则称该点为边界点,例如下图 B 点。
- 而如果某点既不是核心点也不是边界点,则成该点为噪声点,如下图的 C 点。
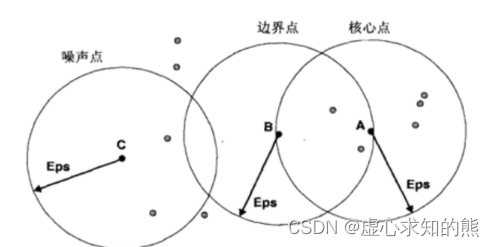
- 当我们对数据集中的所有点完成上述三类的划分之后,接下来,我们一个 eps 范围内的核心点化为一个簇,并且将边界点划归到一个临近的核心点所属簇中,并且抛弃噪声点,最终完成数据集整体的划分。
- 而实际上 DBSCAN 整体划分过程,就是在将高密度区域划分成一个簇,将低密度区域视作不同簇的分界线。
- 很明显,在 DBSCAN 聚类中,核心参数就是 eps 和 min_samples,其不仅可以控制高低密度区域的划分,并且可以实际控制聚成几类的结果:
- 当 eps 较小而 min_samples 较大时,核心点的定义较为严格、同一个簇对簇内的密度要求更高,此时更容易划分出多个簇;反之,划分成的簇的个数可能会更少。
- 接下来我们尝试在 sklearn 进行 DBSCAN 建模试验。
3. DBSCAN 密度聚类的 sklearn 实现
from sklearn.cluster import DBSCANDBSCAN?
- 其中核心参数就是上面介绍的 eps 和 min_samples,其他参数都是距离计算相关和最近邻计算相关的参数,暂时可以不做考虑。接下来围绕上述月牙型数据进行建模:
# 实例化模型
DB = DBSCAN(eps=0.3, min_samples=10)# 训练模型
DB.fit(X)
#DBSCAN(eps=0.3, min_samples=10)# 查看聚类结果
plt.scatter(X[:,0], X[:,1], c = DB.labels_)
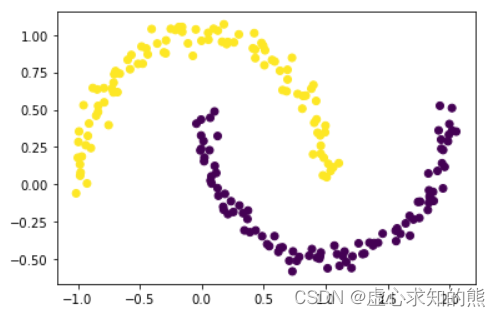
- 能够发现,DBSCAN 通过捕获低密度区域作为聚类划分的边界线,使得最终聚类结果和预想中的情况更加接近。接下来我们尝试在上一小节定义的数据集中执行 DBSCAN 聚类:
np.random.seed(23)
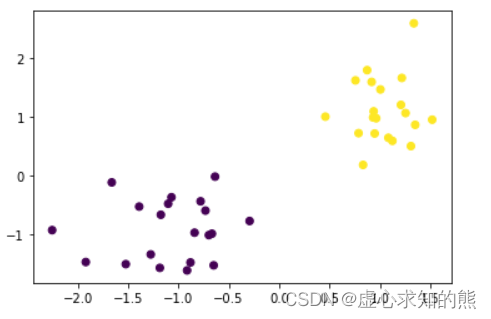
X, y = arrayGenCla(num_examples = 20, num_inputs = 2, num_class = 2, deg_dispersion = [2, 0.5])
plt.scatter(X[:, 0],X[:, 1],c=y)
DB = DBSCAN(eps=0.5, min_samples=5).fit(X)
plt.scatter(X[:,0], X[:,1], c = DB.labels_)
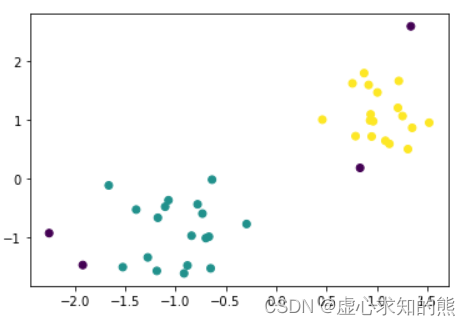
DB.labels_
#array([ 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0,
# 0, -1, 0, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, -1,
# 1, 1, 1, 1, 1, 1])
- 能够发现,DBSCAN 舍弃了一些点(噪声点,标签为 -1),并且将数据聚成两类。
- 当然我们也可以尝试减少 eps、提高 min_samples:
DB = DBSCAN(eps=0.4, min_samples=6).fit(X)
plt.scatter(X[:,0], X[:,1], c = DB.labels_)
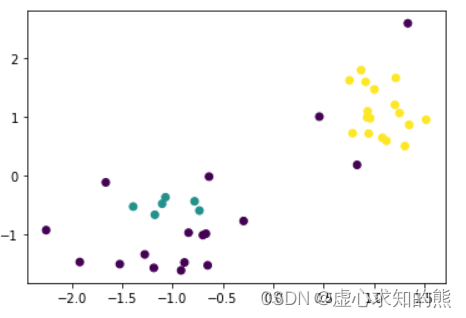
- 此时出现了更多的噪声点,而如果降低密度要求,则会有更多的点被划分到不同的簇中。
DB = DBSCAN(eps=0.6, min_samples=4).fit(X)
plt.scatter(X[:,0], X[:,1], c = DB.labels_)
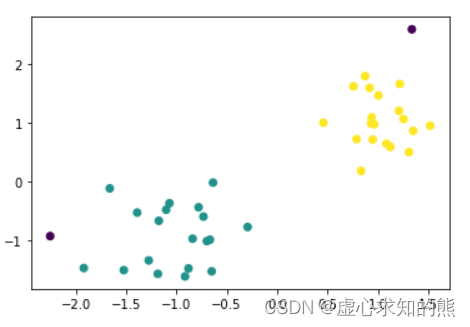
- 至此,我们就完成了 DBSCAN 算法从理论到实践的全过程。
- 还是需要值得一提的是,由于聚类算法的特殊性,导致聚类算法本身的原理和应用难度都远低于有监督学习算法,并且在实际进行聚类的过程中,选择算法的过程要重于调参的过程,而且该过程需要加入实际业务背景作为聚类效果好坏评估的更加具体的指导意见。
- 目前介绍的 K-Means 和 DBSCAN,能够在实际分类性能上形成很好的互补,建议在使用的过程中先尝试 K-Means,如效果不佳,则可考虑尝试使用 DBSCAN 进行聚类。
相关文章:

Lesson 7.2 Mini Batch K-Means与DBSCAN密度聚类
文章目录一、Mini Batch K-Means 算法原理与实现二、DBSCAN 密度聚类基本原理与实践1. K-Means 聚类算法的算法特性2. DBSCAN 密度聚类基本原理3. DBSCAN 密度聚类的 sklearn 实现除了 K-Means 快速聚类意外,还有两种常用的聚类算法。(1) 是能…...

11.Dockerfile最佳实践
Dockerfile 最佳实践 Docker官方关于Dockerfile最佳实践原文链接地址:https://docs.docker.com/develop/develop-images/dockerfile_best-practices/ Docker 可以通过从 Dockerfile 包含所有命令的文本文件中读取指令自动构建镜像,以便构建给定镜像。 …...
【企业云端全栈开发实践-1】项目介绍及环境准备、Spring Boot快速上手
本节目录一、 项目内容介绍二、Maven介绍2.1 Maven作用2.2 Maven依赖2.3 本地仓库配置三、Spring Boot快速上手3.1 Spring Boot特点3.2 遇到的Bug:spring-boot-maven-plugin3.3 遇到的Bug2:找不到Getmapping四、开发环境热部署一、 项目内容介绍 本课程…...
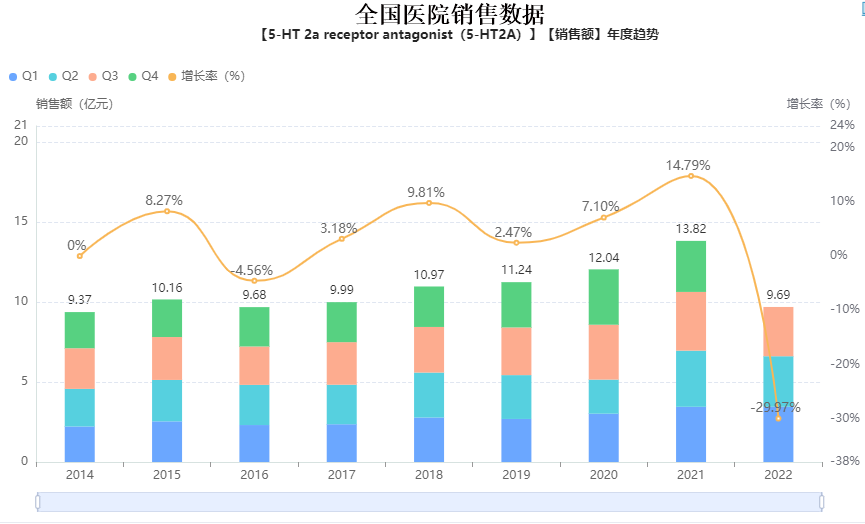
5-HT2A靶向药物|适应症|市场销售-上市药品前景分析
据世界卫生组织称,抑郁症是一种多因素疾病,影响全球约3.5 亿人。中枢神经系统最广泛的单胺 - 血清素 (5-HT) 被认为在这种情况的病理机制中起着至关重要的作用,并且神经递质的重要性被“血清素假说”提升,将抑郁症的存在联系起来 …...

HTTPS协议原理---详解
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
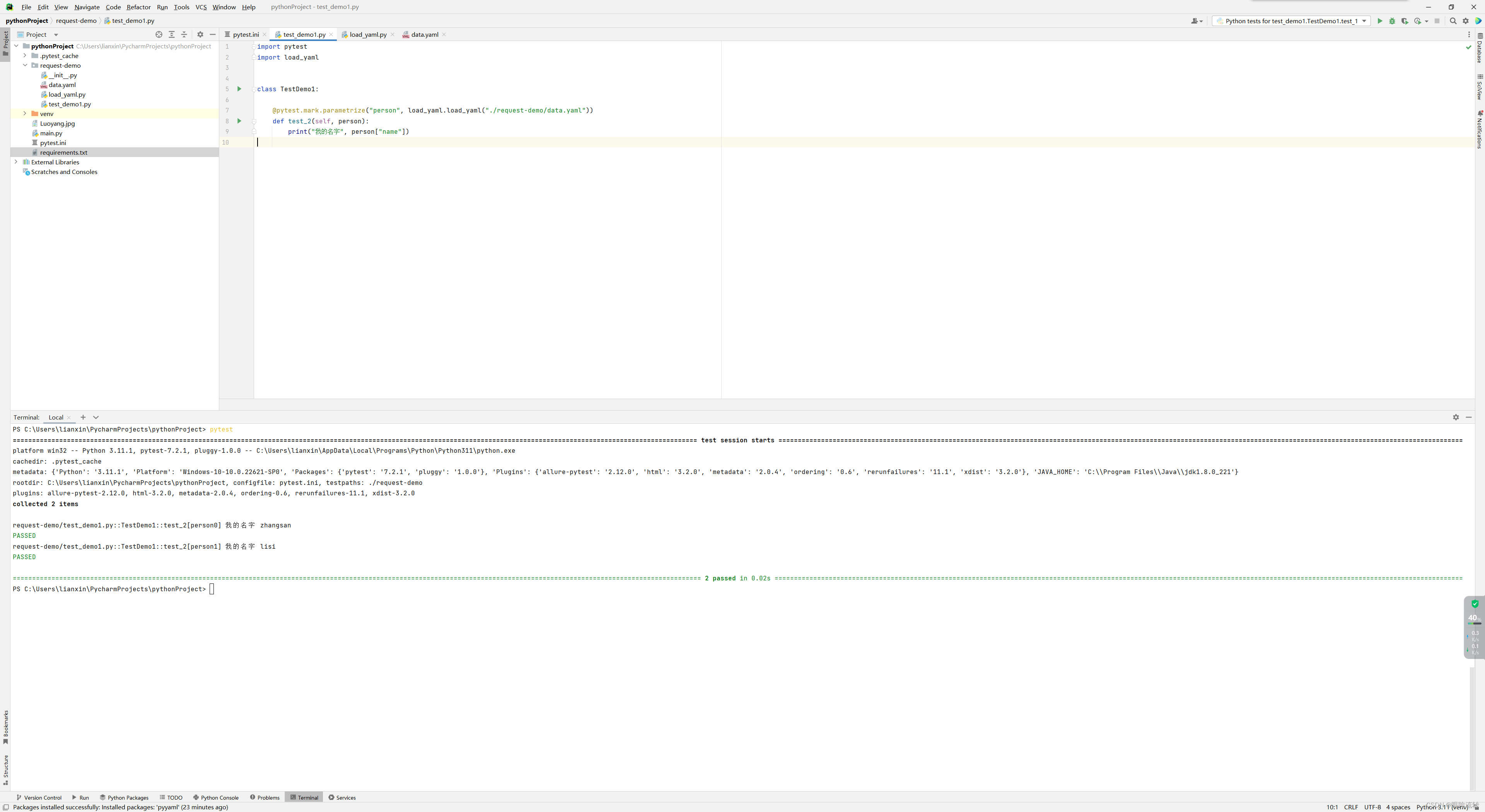
Pytest学习笔记
Pytest学习笔记 1、介绍 1.1、单元测试 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试 1.2、单元测试框架 测试发现:从多个py文件里面去找到我们测试用例测试执行:按…...
Fuzz概述
文章目录AFL一些概念插桩与覆盖率边和块覆盖率afl自实现劫持汇编器clang内置覆盖率反馈与引导变异遗传算法fork server机制AFL调试准备AFL一些概念 插桩与覆盖率 边和块 首先,要明白边和块的定义 正方形的就是块,箭头表示边,边表示程序执行…...
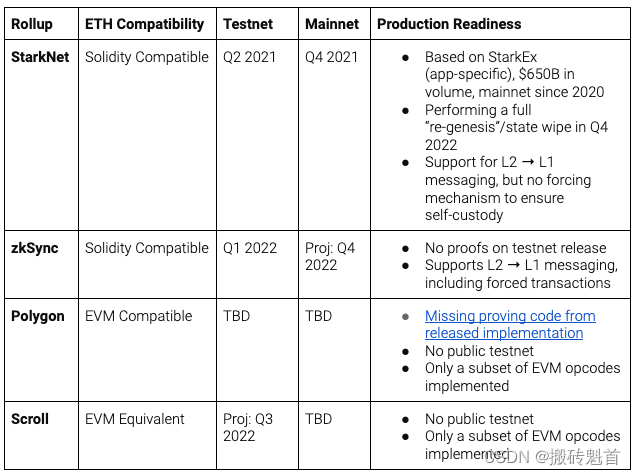
区块链知识系列 - 系统学习EVM(四)-zkEVM
区块链知识系列 - 系统学习EVM(一) 区块链知识系列 - 系统学习EVM(二) 区块链知识系列 - 系统学习EVM(三) 今天我们来聊聊 zkEVM、EVM 兼容性 和 Rollup 是什么? 1. 什么是 Rollup rollup顾名思义,就是把一堆交易卷(rollup)起来…...

Leetcode.2341 数组能形成多少数对
题目链接 Leetcode.2341 数组能形成多少数对 Rating : 1185 题目描述 给你一个下标从 0 开始的整数数组 nums。在一步操作中,你可以执行以下步骤: 从 nums选出 两个 相等的 整数从 nums中移除这两个整数,形成一个 数对 请你在 nums上多次执…...

C++复习笔记10
1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一个元素。 3. list与for…...
leaflet 纯CSS的marker标记,不用图片来表示(072)
第072个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用纯CSS来打造marker的标记。这里用到的是L.divIcon来引用CSS来构造新icon,然后在marker的属性中引用。 这里必须要注意的是css需要是全局性质的,不能被scoped转义为其他随机的css。 直接复制下面的 v…...
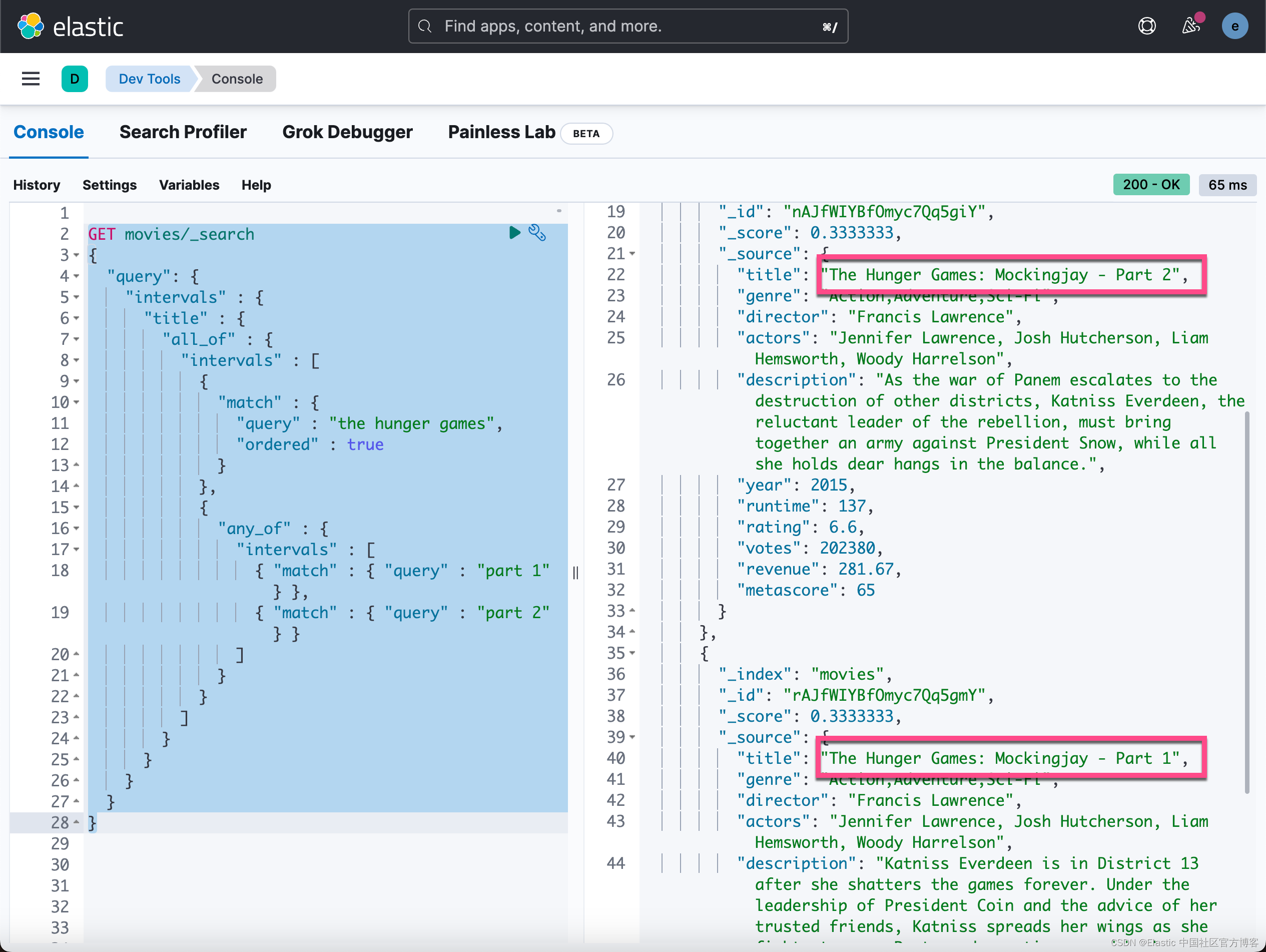
Elasticsearch:使用 intervals query - 根据匹配项的顺序和接近度返回文档
Intervals query 根据匹配项的顺序和接近度返回文档。Intervals 查询使用匹配规则,由一小组定义构成。 然后将这些规则应用于指定字段中的术语。 这些定义产生跨越文本正文中的术语的最小间隔序列。 这些间隔可以通过父源进一步组合和过滤。 上述描述有点费解。我…...
无法决定博客主题的人必看!如何选择类型和推荐的 5 种选择
是否有人不能迈出第一步,因为博客的类型还没有决定?有些人在出发时应该行动,而不是思考,但让我们冷静下来,仔细想想。博客的难度因流派而异,这在很大程度上决定了随后的发展。因此,在选择博客流…...
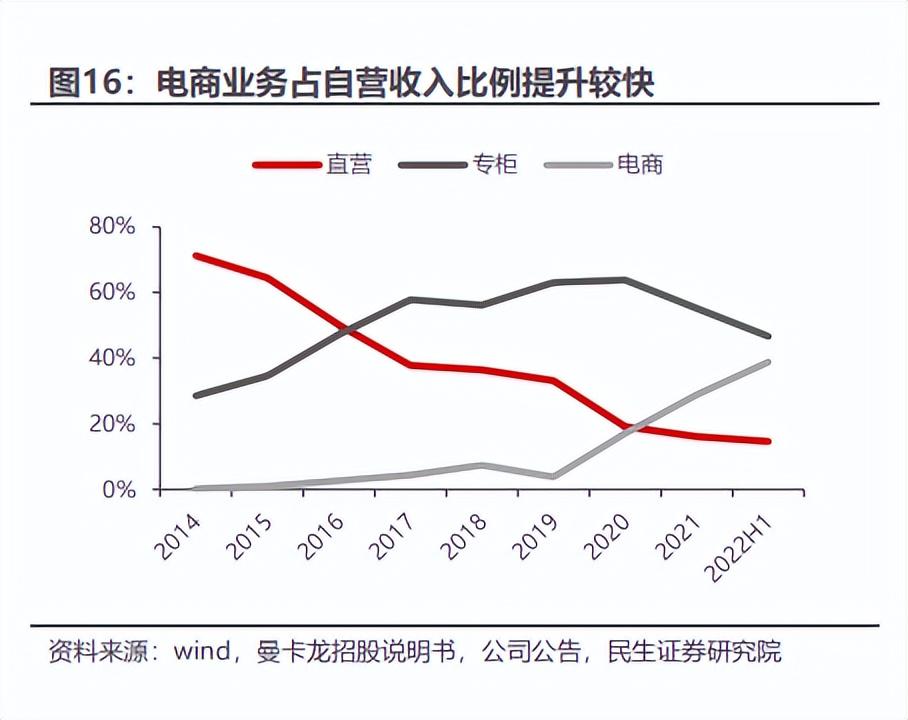
数字化转型的成功模版,珠宝龙头曼卡龙做对了什么?
2月11日,曼卡龙(300945.SZ)发布2022年业绩快报,报告期内,公司实现营业收入16.11亿元,同比增长28.63%。来源:曼卡龙2022年度业绩快报曼卡龙能在2022年实现营收增长尤为不易。2022年受疫情影响&am…...
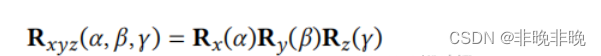
转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录1. 转换矩阵、平移矩阵、旋转矩阵之间的关系2. 缩放变换、平移变换和旋转变换2. python实现旋转矩阵、四元数、欧拉角互相转化由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄…...
中国地图航线图(echarjs)
1、以上为效果图 需要jq、echarjs、china.json三个文件支持。以上 2、具体代码 DOM部分 <!-- 服务范围 GO--> <div class"m-maps"><div id"main" style"width:1400px;height: 800px; margin: 0 auto;"> </div> <!-…...
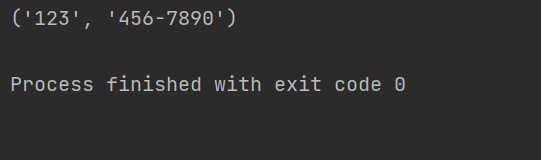
Python正则表达式中group与groups的用法详解
本文主要介绍了Python正则表达式中group与groups的用法详解,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧目录在Python中,正则表达式的group和groups方…...

c++练习题7
1.下列运算符中优先级最高的是 A)> B) C) && D)! 2.以下关于运算符优先级的描述中,正确的是 。 A)!(逻辑非&#x…...

MySQL学习
目录1、数据库定义基本语句(1)数据库操作(2)数据表操作2.数据库操作SQL语句(1)插入数据(2)更新语句(3)删除数据3.数据库查询语句(1)基…...

C语言(强制类型转换)
一.类型转换原则 1.升级:当类型转换出现在表达式时,无论时unsigned还是signed的char和short都会被自动转换成int,如有必要会被转换成unsigned int(如果short与int的大小相同,unsigned short就比int大。这种情况下,uns…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
