【动态规划】背包问题题型及方法归纳
背包问题的种类
背包问题是在规定背包容量为j的前提下,每个物品对应的体积为v[i],价值为w[i],从物品0到物品i中选择物品放入背包中,找出符合某种要求的价值。
(1)背包问题种类
- 01背包:每种物品只能选择1个。
- 完全背包:每种物品可以选择无限个。
- 多重背包:每种物品最多可选s[i]个。
- 分组背包:有若干个组,每组内有若干个物品,每个物品只能选一次。
(2)递推公式
- 01背包:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) - 完全背包:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]) - 多重背包:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i], dp[i - 1][j - 2 * v[i]] + w[i] + ... + dp[i - 1][j - s[i] * v[i]] + s[i] * w[i]) - 分组背包:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i][k] + w[i][k], + ... + dp[i - 1][j - s[i]*v[i][k]] + s[i] * w[i][k])
(3)滚动数组遍历顺序:
遵循原则:用到上一层的信息i-1,则从大到小遍历;用到本层的信息i,则从小到大遍历。
- 01背包:从大到小
- 完全背包:从小到大
- 多重背包:在01背包的基础上,用到i-1层信息,从大到小,多一层for循环选物品个数
- 分组背包:在01背包的基础上,用到i-1层信息,从大到小,多一层for循环选物品个数
1、01背包问题
主要分为两部分:状态表示和状态计算。
1. 状态表示dp[i][j]
i是物品个数,j是条件限制。状态表示一般从两个角度考虑,分别为集合和属性。
其中,集合是只考虑前i个物品,不超过j的选法集合。属性值的是数量、最大值、最小值等。当要求的数到达某一个值时,就要求j - v[i]到达那个相应的值时,会更新,这就要求设置好初始值,一般会让dp[i][0]=0或dp[i][0]=1。
2. 状态计算
状态计算主要是集合划分,分为 f(i-1, j) 所有不选第i个物品的方案和所有选择第i个物品的方案,这种方式可保证不遗漏和不重复。
(1)不超过j的条件下,对于所有不选第i个物品的方案
因为是对i从0开始按顺序遍历,因此选择的是从0-i-1中的选择方案。
(2)不超过j的条件下,所有选择第i个物品的方案
此集合包含两个部分,一个是含有第i个物品,另一个是不含第i个物品从0-i-1中选择的方案。含有第i个物品时,表示的是物品i的体积v[i]为唯一的定量。不含第i个物品时,条件就变为j - v[i],减去了第i个物品的体积,在此条件下,从0-i-1中选,此时会有多种方案,为变量。按我们的目标要求,如果要找最大值,就从多种方案中的一个最大值方案,如果要找最小值,就从多种方案中的最小值方案。两个部分相加,就是我们此方案的结果。
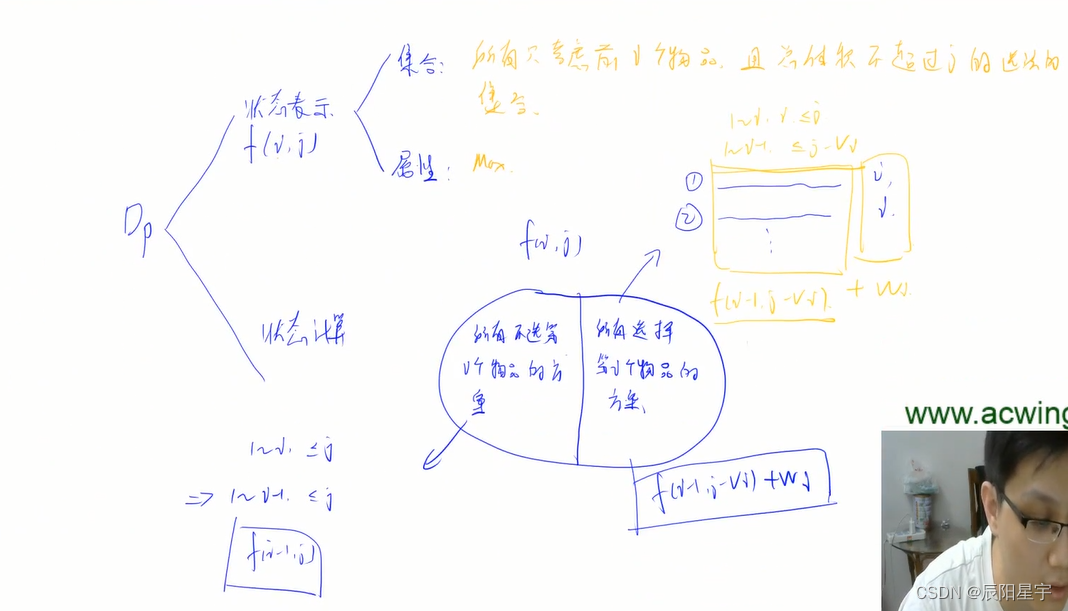
dp[i][j]二维数组
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N][N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 当前物品重量大于背包容量时,不放该物品if(j < v[i]) dp[i][j] = dp[i - 1][j];// 当前物品重量小于等于背包容量时,在放该物品后和不放该物品之间选择一个最大价值else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][m] << endl;return 0;
}
dp[j]一维滚动数组
将dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])改为等价式dp[j] = max(dp[j], dp[j - v[i]] + w[i]),遍历顺序改变为从大到小,通常会初始化dp[0]=0或dp[o]=1。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int dp[N];int main(){int n, m;int v[N], w[N];cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {// 从后向前遍历,表示装入一个物品后,剩余的可装入容量达到的最大价值for(int j = m; j >= v[i]; j--) {dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[m] << endl;return 0;
}151、【动态规划】leetcode ——2. 01背包问题(C++版本):二维数组+滚动数组
拓展应用:
-
152、【动态规划】leetcode ——416. 分割等和子集:滚动数组+二维数组(C++版本):将重量之和除以2,作为背包容量,找到能让背包中可装物体体积最大的装发,让背包中装入物品的重量等于背包容量。
-
153、【动态规划】leetcode ——416. 分割等和子集:滚动数组(C++版本):思路与上一题相同,分割成两个数量相近的集合,最后两个集合的综合相减。
-
154、【动态规划】leetcode ——494. 目标和:回溯法+动态规划(C++版本):分割成正数集合和负数集合,背包容量为正数集合大小,找到可组成正数集合大小的组合方式。
-
155、【动态规划】leetcode ——474. 一和零:三维数组+二维滚动数组(C++版本):字符串作为物品,0和1
2、完全背包问题
与01背包的区别在于同一个物品可以有无限个,对同一个物品可选择多次。
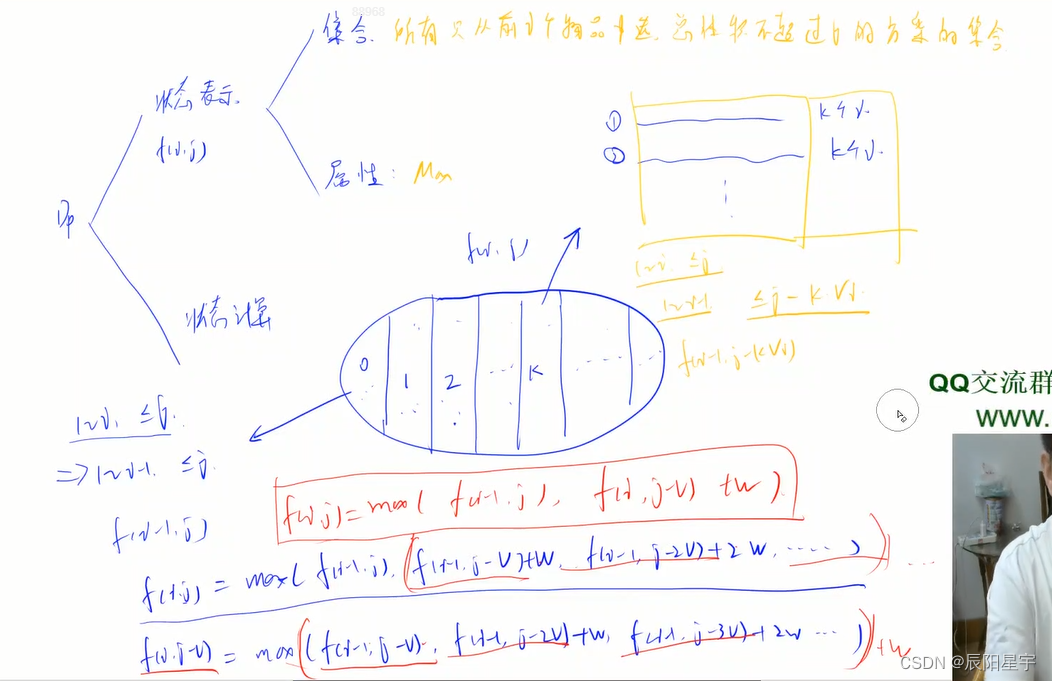
状态计算时,在dp[i][j]情况下 ,划分集合时01背包只能 划分成两个集合 ,而完全背包可以划分为多个集合(第i个物品选择0个、1个、2个…一直到体积达到或超过j为止的多种方案),其中选择0个时,就相当于在0-i-1中选择的方案dp[i - 1][j]。
递推公式表达式为:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + 2*w[i] + ... + dp[i - 1][j - n*v[i]] + n*w[i])(n*v[i]刚好小于等于j)
现在来进行简化,由上式可知,dp[i][j - v[i]] = max(dp[i - 1][j - v[i]], dp[i - 1][j - 2*v[i]] + w[i] + ... + dp[i - 1][j - n*v[i]] + (n-1)*w[i]),对该式两端加上一个w再联立第一个式子,从而得最终简化式子:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
dp[i][j]二维数组
#include <iostream>using namespace std;const int N = 1010;
int dp[N][N];
int v[N], w[N];
int n, m;int main(){cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {for(int j = 1;j <= m; j++) {if(v[i] > j) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);}}cout << dp[n][m] << endl;return 0;
}
d[j]一维滚动数组
滚动数组的遍历顺序按照从小到大遍历。
#include <iostream>using namespace std;const int N = 1010;
int dp[N];
int v[N], w[N];
int n, m;int main(){cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i++) {for(int j = v[i]; j <= m; j++) {// dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[m] << endl;return 0;}
156、【动态规划】AcWing ——3. 完全背包问题:二维数组+一维滚动数组(C++版本)
拓展应用:
无顺序要求的题目:
-
159、【动态规划】leetcode ——322. 零钱兑换:二维数组+一维滚动数组(C++版本):注意求最小值的初始化,由于不考虑顺序问题,因此遍历顺序都可以,dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i]])。
-
160、【动态规划】leetcode ——279. 完全平方数:二维数组+一维滚动数组(C++版本):方式同上,递推公式用上完全平方数形式,dp[i][j] = min(dp[i - 1][j], dp[i][j - i * i] + 1)。
(1)组合问题
组合问题遍历顺序按先背包,再物品遍历
- 158、【动态规划】leetcode ——518. 零钱兑换 II:二维数组+一维滚动数组(C++版本):零钱可以多次使用不考虑数字顺序位置关系,累加计算dp[i][j] = dp[i - 1][j] + dp[i][j - v[i]]。
(2)排列问题
排列问题遍历顺序按先物品,再背包遍历
-
158、【动态规划】leetcode ——377. 组合总和 Ⅳ(C++版本):数字可以多次使用考虑数字顺序位置关系,一维滚动数组累加计算dp[j] += dp[j - v[i]],二维比较特别sum(dp[i][j], dp[i][j - nums[k]),内层需要从0-i再遍历一次。
-
145、【动态规划】leetcode ——70. 爬楼梯:暴力法+动态规划(C++版本):完全背包解法与题2相同,也是排列问题。
-
161、【动态规划】leetcode ——139. 单词拆分:回溯法+动态规划(C++版本):这个题比较奇特一些,当满足前面的字符可以被组成并且当前单词可以有字典中组成时,为dp[j] = true
3、多重背包问题
多重背包是对每种物品的数量进行限制,dp[i][j]的意思:在第i种物品的个数为规定s[i]个的前提下,背包容量为j,物品体积为v[i],从物品0到物品i中选择物品,可达到的最大价值。
实现方式是在01背包实现的基础上,遍历时候,在最内层设置一个for循环,寻找从一个都不选到选s[i]个第i个物品时,哪种情况取得最大价值。
dp[i][j]二维数组
#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n, m;
int dp[N][N];
int v[N], w[N], s[N];int main() {cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 一个都不选一直到选s[i]个,选择一种最大价值情况for(int k = 1; k <= s[i] && j >= k * v[i] ; k++) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * v[i]] + k * w[i]);}}}cout << dp[n][m] << endl;return 0;}d[j]一维滚动数组
#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n, m;
int dp[N];
int v[N], w[N], s[N];int main() {cin >> n >> m;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];dp[0] = 0;for(int i = 1; i <= n; i++) {for(int j = m; j >= 0; j--) {// 一个都不选一直到选s[i]个,选择一种最大价值情况for(int k = 0; k <= s[i] && j >= k * v[i] ; k++) {dp[j] = max(dp[j], dp[j - k * v[i]] + k * w[i]);}}}cout << dp[m] << endl;return 0;}162、【动态规划】AcWing ——4. 多重背包问题 I(C++版本)
4、分组背包
分组背包问题是在01背包的基础上,多了一个组的概念。有若干个组,每组里面有若干个物品,每个物品只能选择一次,找到在背包容量为j的前提下,从0-i组中选择物品,达到背包里价值最大。
d[j]一维滚动数组
#include <iostream>
#include <algorithm>using namespace std;const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int dp[N];int main() {cin >> n >> m;for(int i = 1; i <= n; i++) {cin >> s[i];for(int j = 0; j < s[i]; j++) {cin >> v[i][j] >> w[i][j];}}for(int i = 1; i <= n; i++) { // 遍历物品for(int j = m; j >= 1; j--) { // 从大到小,遍历背包(使用i-1层信息)for(int k = 0; k < s[i]; k++) { // 遍历每组内的物品个数if(j >= v[i][k]) {dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]);}}}}cout << dp[m] << endl;return 0;
}
166、【动态规划】AcWing ——9. 分组背包问题(C++版本)
相关文章:

【动态规划】背包问题题型及方法归纳
背包问题的种类 背包问题是在规定背包容量为j的前提下,每个物品对应的体积为v[i],价值为w[i],从物品0到物品i中选择物品放入背包中,找出符合某种要求的价值。 (1)背包问题种类 01背包:每种物…...
全球十大资质正规外汇期货平台排行榜(最新版汇总)
外汇期货简称为FxFut,是“Forex Futures”的缩写,是在集中形式的期货交易所内,交易双方通过公开叫价,以某种非本国货币买进或卖出另一种非本国货币,并签订一个在未来的某一日期根据协议价格交割标准数量外汇的合约。 …...

使用Paramiko时遇到的一些问题
目录 1.背景 2.问题合集 1)“bash: command not found” 2)Paramiko中正常的输入,却到了stderr,而stdout是空 3)命令实际是alias 1.背景 在自动化脚本中,使用了库Paramiko,远程SSH到后台服…...

数据预处理(无量纲化、缺失值、分类特征、连续特征)
文章目录1. 无量纲化1.1 sklearn.preprocessing.MinMaxScaler1.2 sklearn.preprocessing.StandardScaler2. 缺失值3. 分类型特征4. 连续型特征数据挖掘的五大流程包括:获取数据数据预处理特征工程建模上线 其中,数据预处理中常用的方法包括数据标准化和归…...

【C#基础】C# 运算符总结
序号系列文章2【C#基础】C# 基础语法解析3【C#基础】C# 数据类型总结4【C#基础】C# 变量和常量的使用文章目录前言运算符1,算术运算符2,布尔逻辑运算符3,位运算符4,关系运算符5,赋值运算符6,其他运算符7&am…...
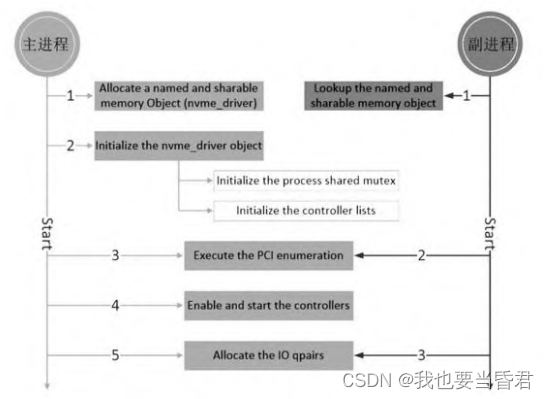
存储性能软件加速库(SPDK)
存储性能软件加速库SPDK存储加速存储性能软件加速库(SPDK)SPDK NVMe驱动1.用户态驱动1)UIO2)VFIOIOMMU(I/O Memory Management Unit)3)用户态DMA4)大页(Hugepage…...
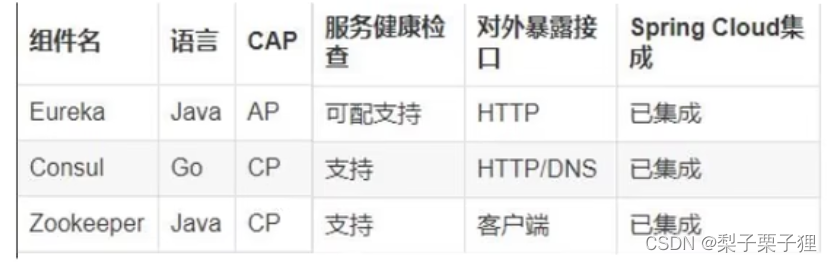
微服务(五)—— 服务注册中心Consul
一、引入依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-consul-discovery</artifactId></dependency>二、配置yml文件 server:port: 8006spring:application:name: cloud-payment-con…...
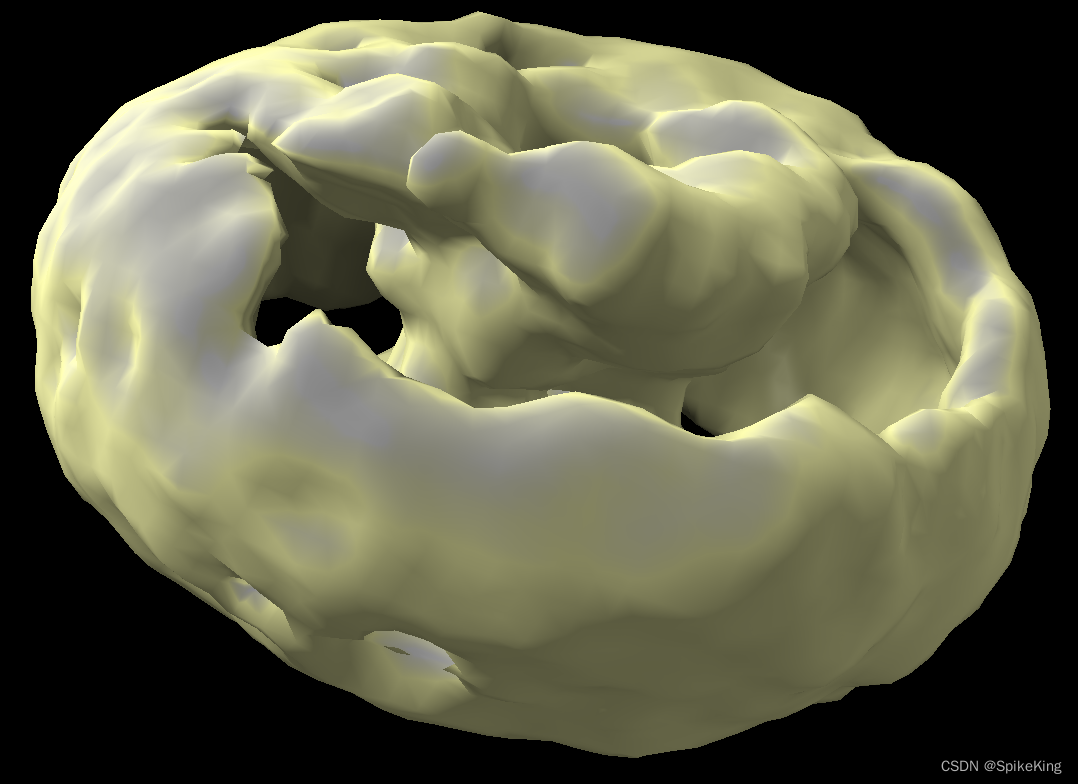
冷冻电镜 - ChimeraX Density Map 密度图 操作
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/129055160 由冷冻电镜所生成的Volume,需要观察其内部结构,使用ChimeraX进行操作。 加载Volumes,例如my_volume.mrc 效果如下: 高斯滤波 在命令行(Co…...

Matlab 点云旋转之轴角式
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 三维空间中表示旋转的方法有很多种,轴角式是其中非常经典的一种表示方式。虽然欧拉角表示旋转的方法很是常用,但欧拉角存在着万向锁这个问题,因此轴角式旋转在旋转使用中更为合适。其原理也很是明了,如下所述:…...
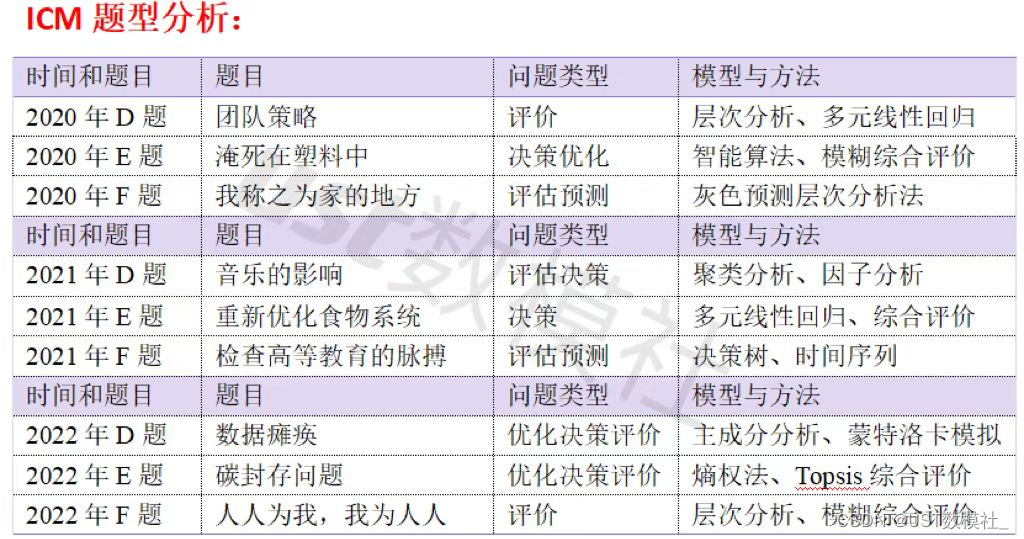
2023美赛数学建模资料思路模型
美赛我们为大家准备了大量的资料,我们会在比赛期间给大家分析美题目和相关的思路 全文都是干货,大家仔细阅读,资料文末自取! 首先我们来看美赛23年题型的一个变化: 美赛23年题目变化: A题:连…...

Nginx配置HTTP强制跳转到HTTPS
https 访问我们的测试域名 https://www.xxx.com 站点,但是当我们直接在浏览器地址栏中直接输入 www.xxx.com 的时候却发现进入的是 http 协议的网站,这与我们的初衷不一致。由于浏览器默认访问域名使用的是80端口,而当我们使用SSL证书后&…...

从实现到原理,聊聊Java中的SPI动态扩展
原创:微信公众号 码农参上,欢迎分享,转载请保留出处。 八股文背多了,相信大家都听说过一个词,SPI扩展。 有的面试官就很喜欢问这个问题,SpringBoot的自动装配是如何实现的? 基本上,…...

3、MySQL字符集
1.MySQL字符集和校验规则 字符集:是一套符号和编码的规则校验规则:是对该套符号和编码的校验,定义字符的排序和比较规则,其中是否区分大小写,跟校验规则有关。2.查看字符集方法 netstat -lntup |grep 3306 tcp6 0 0 :::3306 :::* …...
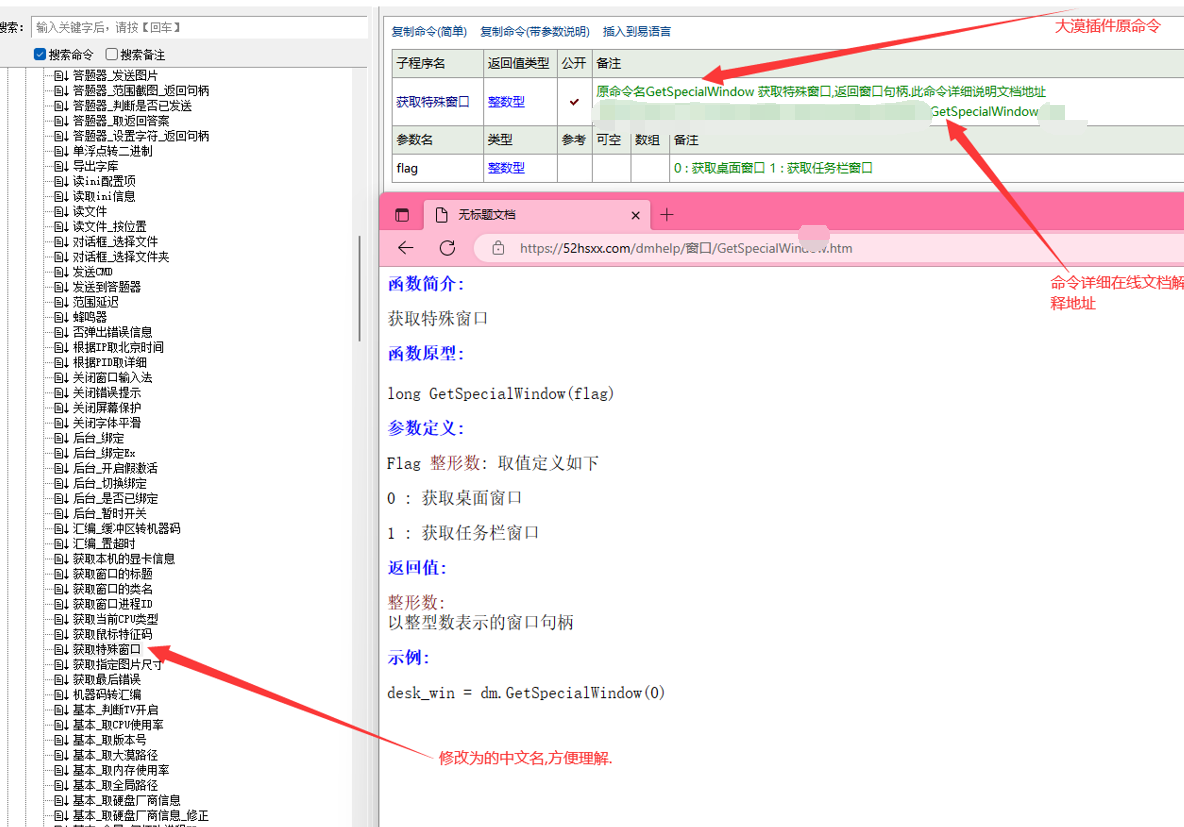
大漠插件最新中文易语言模块7.2302
模块名称:大漠插件中文模块最新通用7.2302模块简介:大漠插件中文模块最新通用7.2302模块特色:原翻译:花老板完善命令备注:易生易世本人花费一个月时间才将命令完善了插件的备注说明.且用且珍惜去掉了大漠插件定制版类.因为没用.模块特色:什么是中文模块?大漠插件模块是由大漠类…...
极客大挑战 2021
题量很大,收获挺多,持续时间也长,据说结束之后会再持续一段时间,然后题目会开源。 WEB Dark 暗网签到,难以置信 Welcome2021 改个请求方法会提示你文件,再进去就好了 babysql 直接把请求包扔sqlmap里&…...

C#开发的OpenRA加载文件的管理
C#开发的OpenRA加载文件的管理 在前面我们分析了mod.yaml文件,发现里面有很多文件列表, 比如下像下面的文件: Packages: ~^SupportDir|Content/cnc ~^SupportDir|Content/cnc/movies ^EngineDir $cnc: cnc ^EngineDir|mods/common: common ~speech.mix ~conquer.mix ~sounds…...

SSM实现文件上传
目录 SSM实现文件上传 1、修改from表单请求方式改为post,添加属性 2、修改springmvc配置文件,添加一下配置 3、后端方法 SSM实现文件上传 1、修改from表单请求方式改为post,添加属性: enctype"multipart/form-data"…...

OPENCV计算机视觉开发实践-图像的基本概念
1.图像与图形: 图像->客观世界的反映,图与像之结合 图->物体透射光与反射光的分布 像->人的视觉得对图的认识 图像->通过照相,摄像,扫描产生. 图形->通过数学规则产生,或者具有一定规则的图案.用一组符号或线条表示性质. 2.数字图像: 数字图像->称数码图像或…...

Android 9.0 ResolverActivity.java多个app选择界面去掉始终保留仅有一次
1.前言 在9.0的系统rom定制化开发过程中,在系统中安装同类型多个app的时候,在系统启动的过程中,会在启动launcher或播放器的过程中,在启动的过程中都是弹出选择框的,然后在选择启动哪个app,这些选择都是在ResolverActivity.java中完成的,所以需要在ResolverActivity.java…...

【算法 | 例题简答】相关例题讲解
目录 简答题 计算题 时间复杂度的计算 递归算法计算 背包问题(0-1背包问题) 回溯法 动态规划法 编程题 用回溯法解方程 动态规划法解决蜘蛛吃蚊子 用分治法解决抛硬币问题 用二分法分两边求最大值 简答题 1、什么是算法?算法有哪…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
