【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】
💃🏼 本人简介:男
👶🏼 年龄:18
📕 ps:七八天没更新了欸,这几天刚搞完元宇宙,上午一直练🚗,下午背四级单词和刷题来着,还在忙一些学弟学妹录制视频和准备开学一些事,一直没空出时间来,等 20号练完车,也马上开学了QAQ。不过今天倒是空出来一些时间,恰好这几天学到了dfs,原理和例题都很棒,谨以此篇作为学后的回顾总结!
文章目录
- 1. dfs算法原理
- 1.1 dfs思想
- 1.2 与递归区别
- 1.3 举例说明
- 2. 经典例题——迷宫游戏
- 2.1 题干信息
- 2.2 整体思路
- 2.3 细分拆解
- ①判断迷宫终点,记录所走路径
- ②完善搜索与回溯,处理数组边界
- ③找寻迷宫起点,打印结束路径
- 2.4 总体代码展示
- 2.5 测试样例
- 2.6 代码优化
- 最后,感谢大家支持u (^ _ ^)
1. dfs算法原理
1.1 dfs思想
- 深度优先搜索,简称dfs,简单讲就是一个搜索算法。
- 深搜是按照
深度优先的方式进行搜索,通俗来讲就是一条路走到黑和不撞南墙不回头。 - 注意:这里的
搜索并不是我们平时在文件上或网络上查找信息,而是通过一种穷举的方式,把所有可行的方案都列举出来,不断去尝试,直到找到问题的解。 - 具体来讲,dfs可以将“问题状态空间”看做一棵搜索树,深度优先就是从
树根一直往下搜,遇到不可解就回溯,往其它方向继续向下扩展,像子集和和全排列问题,还有N皇后问题都可以深度优先搜索算法解决,它是一种暴力解决NP问题的非常直观的方法。 - 总的来说:DFS 用于找所有解的问题,它的空间效率高,而且找到的不一定是最优解,必须记录并完成整个搜索,故一般情况下,深搜需要非常高效的剪枝(剪枝的概念请百度)。
1.2 与递归区别
- 深搜是一种算法,注重的是思想;而递归是一种基于编程语言的实现方式。
- 深搜可以用递归实现,也就是说递归是我们用计算机编程语言实现深搜算法的手段。
1.3 举例说明
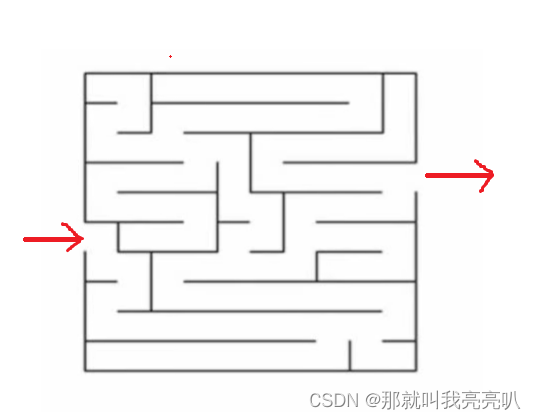
如下图,灰色代表墙壁,绿色代表起点,红色代表终点,规定每次只能走一步,且只能往下或右走。求一条绿色到红色的最短路径。例子来源于这里
用dfs来讲就是,先从绿点开始找准一个方向,并沿这个方向一直遍历,如果遇到障碍物不能继续遍历就回溯,返回上一个节点,直到找到终点为止。
2. 经典例题——迷宫游戏
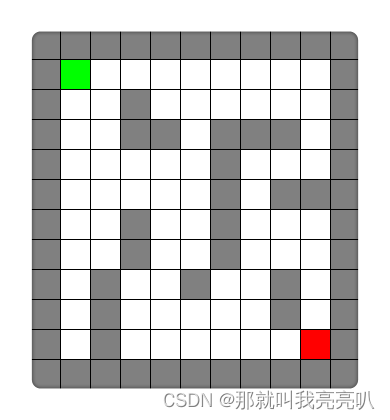
都学了这么多了。我们不妨来玩一个迷宫游戏巩固一下所学的算法!【迷宫如图下所示】
最短的解法如下图所示【大家答对了嘛】
2.1 题干信息
- 我们用一个二维字符数组来表示图画的迷宫。
S**.
....
***T
- 其中
S表示起点,T表示终点,*表示墙壁,.表示平地。你需要从S出发走到T,每次只能向上下左右相邻的位置移动一位,不能走出地图,也不能穿过墙壁,每个点只能通过一次。用x表示你所要走的路线。
2.2 整体思路
- 我们从起点S开始,每走一步需要对上下左右一个方向一个方向地尝试,如果沿着某个方向不能走到终点,我们就要原路返回,继续尝试其他方向,直到走出迷宫。这是一种最朴素的走迷宫方式,虽然效率也许比较低,但如果迷宫有解,就一定能走出终点。
- 上面说的这种走法,就对应着今天学习的dfs算法。首先找到起点s,走到每个点时,按照左、下、右、上的顺序尝试。每走到下一个点以后,我们把这个点当做起点S,继续按顺序尝试。如果某个点上下左右四个方向都尝试过,便回到走到这个点之前的点,这一步我们称之为回溯。继续尝试其他方向。直到所有点都尝试过上下左右四个方向。
- 这就好比你自己去走这个迷宫,你也要一个方向一个方向的尝试着走,如果这条路不行就回头,尝试下一条路,dfs 的思想和我们直观的想法很类似。只不过,接下来我们需要用程序来完成这个过程。
2.3 细分拆解
第一步前的输入地图和变量设置,就不详细讲了,直接看代码即可
#include<iostream>
#include<stdio.h>
using namespace std;
int n, m;
char pos[150][150]; //判断走没走过
bool trace[150][150]; //显示路径int main() {//输入地图cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];}}return 0;
}①判断迷宫终点,记录所走路径
- 首先确定边界条件,当走到字符
T时,我们找到了终点,从而结束搜索。所以边界条件判断为pos[x][y] == 'T'。 - 其次,为了防止走回头路,我们需要标记当前这个路径已走过,即当前这个点已走过,所以我们需要用
trace[x][y]数组来做标记,为了显示出路径,走过的点我们用字符x表示。
bool dfs(int x, int y) {if (pos[x][y] == 'T') { //找到终点,返回truereturn true;}trace[x][y] = 1; //若找不到,则trace数组标记为1表示已走过pos[x][y] = 'x'; //用pos显示最后的路径
}
②完善搜索与回溯,处理数组边界
- 结束操作处理好后,就要开始真正的搜索了。假设现在我们坐标为
(x, y),分别遍历该坐标的上下左右位置,选择好依次进行方向的顺序后,一个方向一个方向进行访问,如果某一方向能走到终点,则返回true。 - 在上下左右遍历时,我们要考虑数组元素是否越界,此时我们就需要一个
bool类型的check_in()函数进行判断。 - 注意:判断移动后位置能走的3个条件【缺一不可】
- ①没越界,在地图内;
- ②这个位置不是障碍物*,可以走到;
- ③该位置之前没走过
bool check_in(int x, int y) { // 判断数组是否越界return (x > 0 && x <= n && y > 0 && y <= m); //这里表示的是如果()里为真,则返回true,否则返回false
}bool dfs(int x, int y) {if (pos[x][y] == 'T') { //找到终点,返回truereturn true;}trace[x][y] = 1; //若上下左右都找不到,则trace数组标记为1表示已走过pos[x][y] = 'x'; //用pos显示最后的路径int tx = x - 1, ty = y; //假设先往上走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) { //能移动到该位置的条件有三个:①没越界,在地图内; ②这个位置不是障碍物*,可以走到; ③该位置之前没走过if (dfs(tx, ty)) { //对移动后位置进行判断是不是终点,如果是,返回true,如果不是,在对其上下左右判断。return true;}}tx = x, ty = y - 1; //如果往上走行不通,则选择向左走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}tx = x + 1, ty = y; //如果往左走行不通,则选择向下走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}tx = x , ty = y + 1; //如果往下走行不通,则选择向右走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}pos[x][y] = '.'; // 如果一个位置的上下左右都走不了,则取消该位置的路径进行回溯,回溯过程把之前已标记的'x'改回'.'trace[x][y] = 0;//只找可行路线的话,trace可改可不改。但如果找全部解,则需要恢复return false;
}
大家有没有发现判断上下左右是否可行时,主题代码是不是都是一样的欸?所以大家可以想一下,能怎么去优化一下嘛,在这里我卖个关子,咱们后面马上讲!
③找寻迷宫起点,打印结束路径
- 我们费心费力地把迷宫主体的dfs的函数写完了,但我们该从哪开始呢?结束条件如何设置呢?
int main() {//输入地图cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];}}cout << "----------------------------------------" << endl;//找寻起点int x , y ; //定义x,y用于保存迷宫起点时的位置for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (pos[i][j] == 'S') {x = i, y = j;}}}if (dfs(x, y)) { //如果能找到终点,则打印迷宫显示其路径cout << "鼠鼠我欸,已到达终点啦,路线如下: " << endl;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << pos[i][j];} cout << endl;}}else {cout << "鼠鼠我欸,走不出去啦awa" << endl;}return 0;
}
2.4 总体代码展示
#include<iostream>
#include<stdio.h>
using namespace std;int n, m;
char pos[150][150]; //判断走没走过
bool trace[150][150]; //显示路径bool check_in(int x, int y) { // 判断数组是否越界return (x > 0 && x <= n && y > 0 && y <= m); //这里表示的是如果()里为真,则返回true,否则返回false
}bool dfs(int x, int y) {if (pos[x][y] == 'T') { //找到终点,返回truereturn true;}trace[x][y] = 1; //若上下左右都找不到,则trace数组标记为1表示已走过pos[x][y] = 'x'; //用pos显示最后的路径int tx = x - 1, ty = y; //假设先往上走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) { //能移动到该位置的条件有三个:①没越界,在地图内; ②这个位置不是障碍物*,可以走到; ③该位置之前没走过if (dfs(tx, ty)) { //对移动后位置进行判断是不是终点,如果是,返回true,如果不是,在对其上下左右判断。return true;}}tx = x, ty = y - 1; //如果往上走行不通,则选择向左走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}tx = x + 1, ty = y; //如果往左走行不通,则选择向下走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}tx = x , ty = y + 1; //如果往下走行不通,则选择向右走if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}pos[x][y] = '.'; // 如果一个位置的上下左右都走不了,则取消该位置的路径进行回溯,回溯过程把之前已标记的'x'改回'.'trace[x][y] = 0;//只找可行路线的话,trace可改可不改。但如果找全部解,则需要恢复return false;
}
int main() {//输入地图cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];}}cout << "----------------------------------------" << endl;//找寻起点int x , y ; //定义x,y用于保存迷宫起点时的位置for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (pos[i][j] == 'S') {x = i, y = j;}}}if (dfs(x, y)) { //如果能找到终点,则打印迷宫显示其路径cout << "鼠鼠我欸,已到达终点啦,路线如下: " << endl;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << pos[i][j];} cout << endl;}}else {cout << "鼠鼠我欸,走不出去啦awa" << endl;}return 0;
}
2.5 测试样例
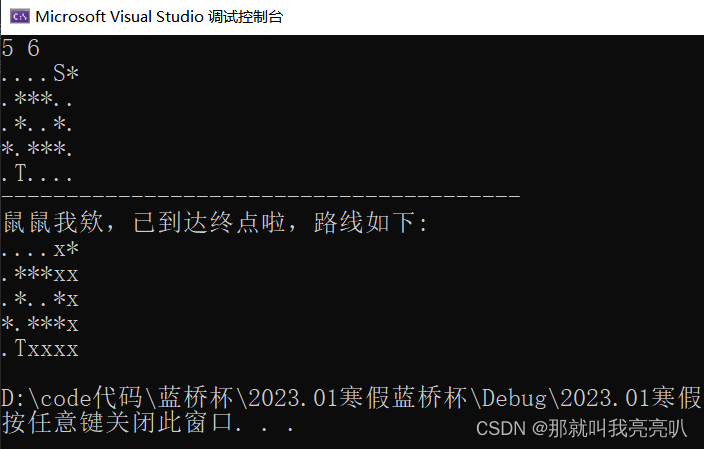
2.6 代码优化
- 前面提到,我们在对下一位置进行上下左右判断时,需要写四个主体相同的代码。为了减少代码量,我们不妨写一个循环,用一个二维数组依次表示四个方向,进而进行判断。
int dir[4][2] = { { -1 , 0 } , { 0 , -1 } , { 1 , 0 } , { 0 , 1 } };
// 按逆时针依次表示 向上 向左 向下 向右
//第一个数表示x(行)变化,第二个表示y(列)变化
bool dfs(int x, int y) {if (dfs(x, y) == 'T') {return true;}trace[x][y] = 1;pos[x][y] = 'x';for (int i = 1; i <= 4; i++) { //1、2、3、4依次表示上、左、下、右int tx = x + dir[i][0]; //表示x加上第几个方向的第1个数,即行变化,int ty = y + dir[i][1]; //表示x加上第几个方向的第2个数,即列变化,if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}}pos[x][y] = '.'; // 如果一个位置的上下左右都走不了,则取消该位置的路径进行回溯,回溯过程把之前已标记的'x'改回'.'trace[x][y] = 0;//只找可行路线的话,trace可改可不改。但如果找全部解,则需要恢复
}
优化后代码
#include<iostream>
#include<stdio.h>
using namespace std;int n, m;
char pos[150][150]; //判断走没走过
bool trace[150][150]; //显示路径int dir[4][2] = { { -1 , 0 } , { 0 , -1 } , { 1 , 0 } , { 0 , 1 } };
// 按逆时针依次表示 向上 向左 向下 向右
//第一个数表示x(行)变化,第二个表示y(列)变化bool check_in(int x, int y) { // 判断数组是否越界return x > 0 && x <= n && y > 0 && y <= m; //这里表示的是如果()里为真,则返回true,否则返回false
}bool dfs(int x, int y) {if (dfs(x, y) == 'T') {return true;}trace[x][y] = 1;pos[x][y] = 'x';for (int i = 1; i <= 4; i++) { //1、2、3、4依次表示上、左、下、右int tx = x + dir[i][0]; //表示x加上第几个方向的第1个数,即行变化,int ty = y + dir[i][1]; //表示x加上第几个方向的第2个数,即列变化,if (check_in(tx, ty) && pos[tx][ty] != '*' && !trace[tx][ty]) {if (dfs(tx, ty)) {return true;}}}pos[x][y] = '.'; // 如果一个位置的上下左右都走不了,则取消该位置的路径进行回溯,回溯过程把之前已标记的'x'改回'.'trace[x][y] = 0;//只找可行路线的话,trace可改可不改。但如果找全部解,则需要恢复}int main() {//输入地图cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];}}cout << "----------------------------------------" << endl;//找寻起点int x , y ; //定义x,y用于保存迷宫起点时的位置for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (pos[i][j] == 'S') {x = i, y = j;}}}if (dfs(x, y)) { //如果能找到终点,则打印迷宫显示其路径cout << "鼠鼠我欸,已到达终点啦,路线如下: " << endl;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << pos[i][j];} cout << endl;}}else {cout << "鼠鼠我欸,走不出去啦awa" << endl;}return 0;
}最后,感谢大家支持u (^ _ ^)
如果感觉这篇文章对你有帮助的话,不妨三连支持下,十分感谢(✪ω✪)。
printf("点个赞吧*^*");
cout << "收藏一下叭o_o";
System.out.println("评论一下吧^_^");
print("关注一下叭0-0")
相关文章:

【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】
💃🏼 本人简介:男 👶🏼 年龄:18 📕 ps:七八天没更新了欸,这几天刚搞完元宇宙,上午一直练🚗,下午背四级单词和刷题来着,还在忙一些学弟…...
总结高频率Vue面试题
目录 什么是三次握手? 什么是四次挥手?(close触发) 什么是VUEX? 什么是同源----跨域? 什么是Promise? 什么是fexl布局? 数据类型 什么是深浅拷贝? 什么是懒加载&…...
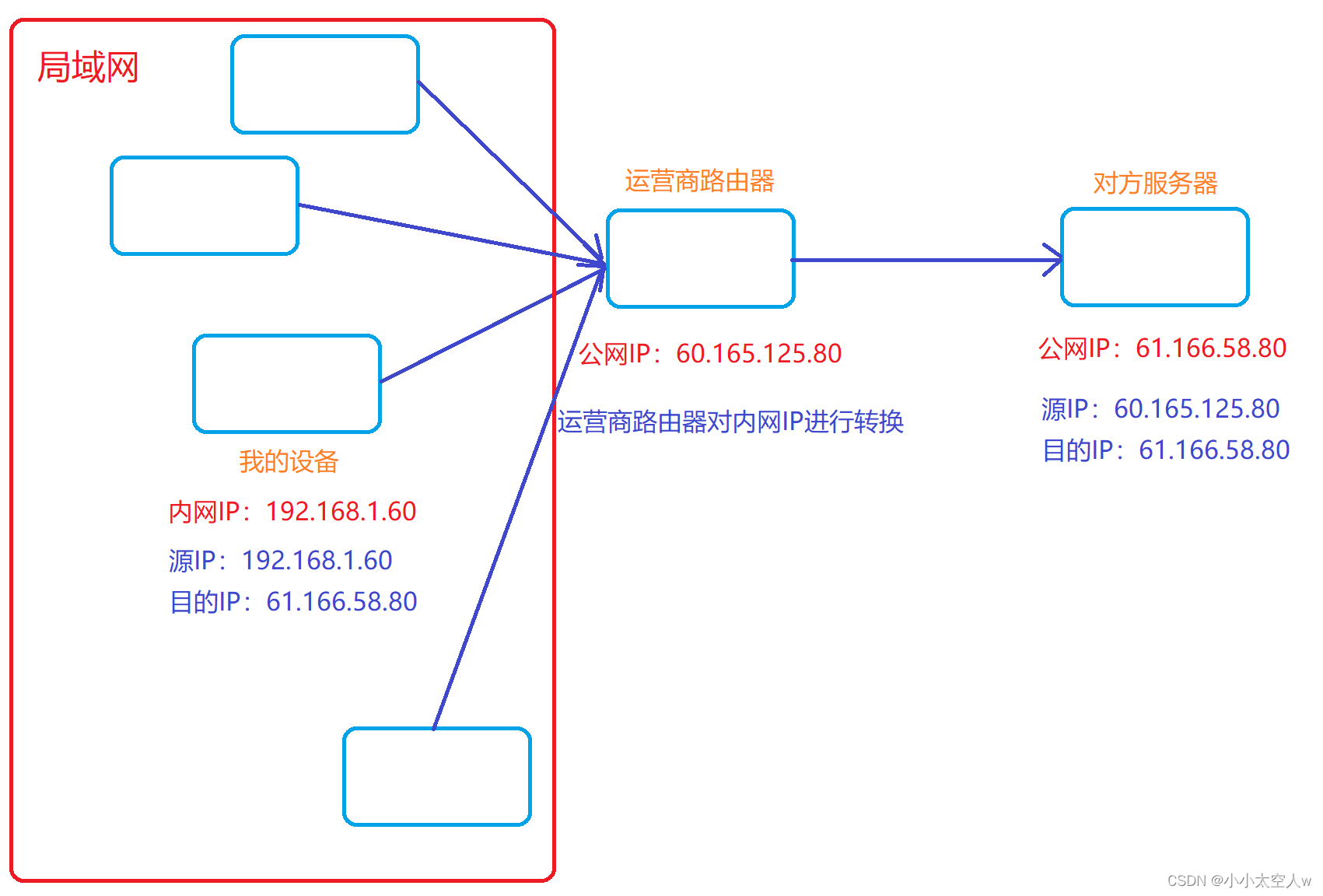
IP协议详解
目录 前言: IP协议 提出问题 解决方案 地址管理 子网掩码 路由选择 小结: 前言: IP协议作为网络层知名协议。当数据经过传输层使用TCP或者UDP对数据进行封装,然后当数据到达网络层,基于TCP或UDP数据包继续进行…...
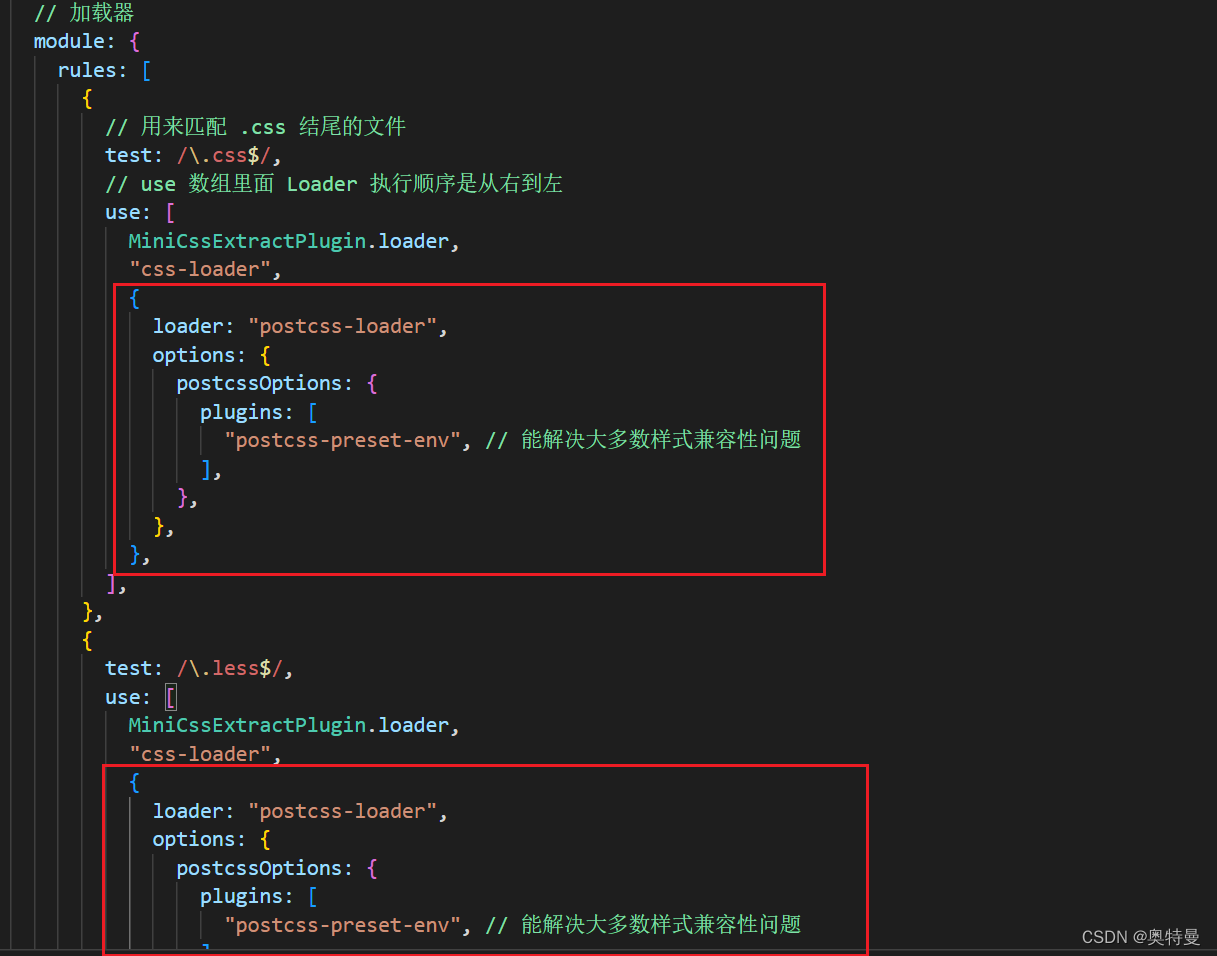
webpack5 基础配置
在开发中,我们会使用 vue、react、less、scss等语法进行开发项目,但是浏览器只能识别 js、css,或者说在js中使用了es6中的import 导入 这时候也需要打包工具去转换成浏览器可以识别的语句。 一、使用webpack 1.初始化package.json npm i…...
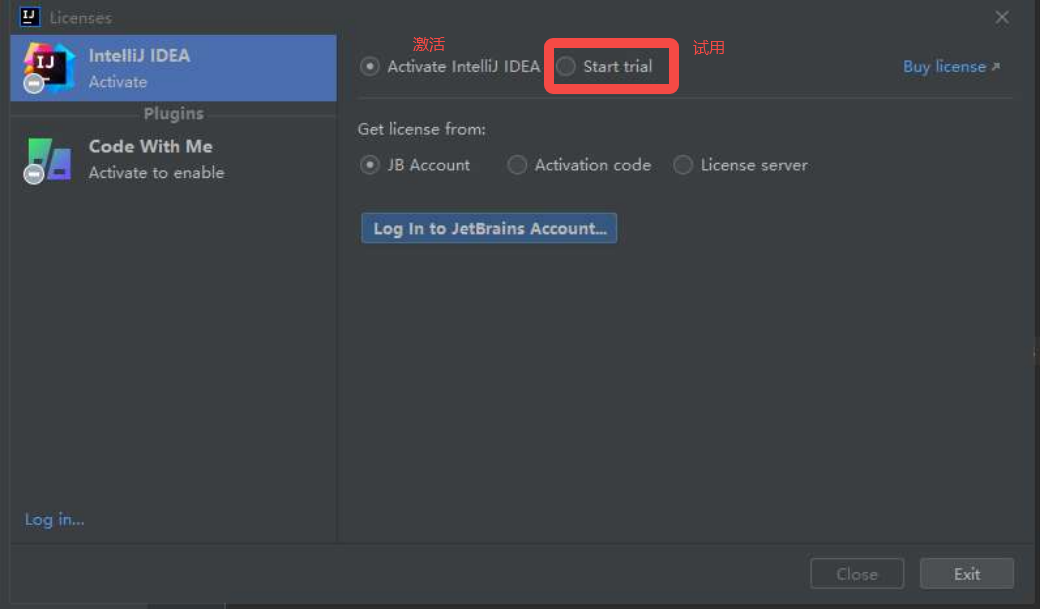
IDEA入门安装使用教程
一、背景 作为一个Java开发者,有非常多编辑工具供我们选择,比如Eclipse、IntelliJ IDEA、NetBeans、Visual Studio Code、Sublime Text等等,这些有免费也有收费的,但是就目前市场占比来说普遍使用Eclipse和IntelliJ IDEA这两款主…...

Lambda表达式使用及详解
一 Lambda表达式的简介 Lambda表达式(闭包):java8的新特性,lambda运行将函数作为一个方法的参数,也就是函数作为参数传递到方法中。使用lambda表达式可以让代码更加简洁。 Lambda表达式的使用场景:用以简…...

JAVA练习52-打家劫舍
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-打家劫舍 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 2月16日练习内容 提…...

简单谈一谈幂等测试
1、什么是幂等测试 幂等是一个抽象的概念,在编程中一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同,即多次调用方法或者接口不会改变业务状态,可以保证重复调用的结果和单次调用的结果一致。幂等测试,则主…...

typescript复习笔记
数组类型-限定每一项的类型 //写法一 const arrNumber: number[] [1, 2, 3] const arrString: string[] [a, b, c] //写法二 const arrNumber2: Array<number> [1, 2, 3] const arrString2: Array<string> [a, b, c]联合类型 符号是 | //数组可以存放字符串或…...
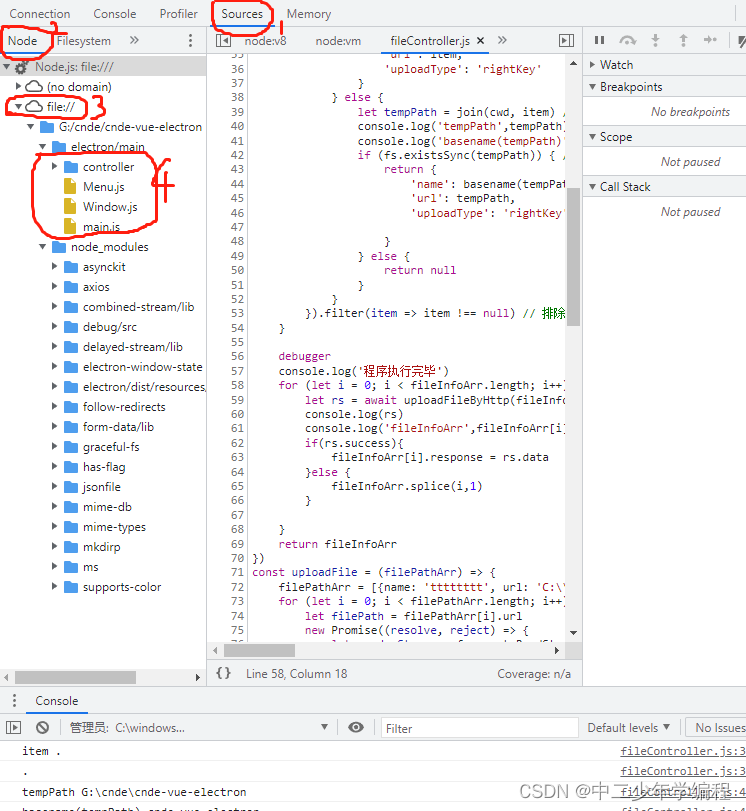
webstorm开发electron,调试主进程方案
官网教程地址:https://www.electronjs.org/zh/docs/latest/tutorial/debugging-main-process 我只能说官网太看得起人了,整这么简易的教程…… 命令行开关 第一步还是要按要求在我们的package.json里加上端口监听:–inspect5858 我的命令…...
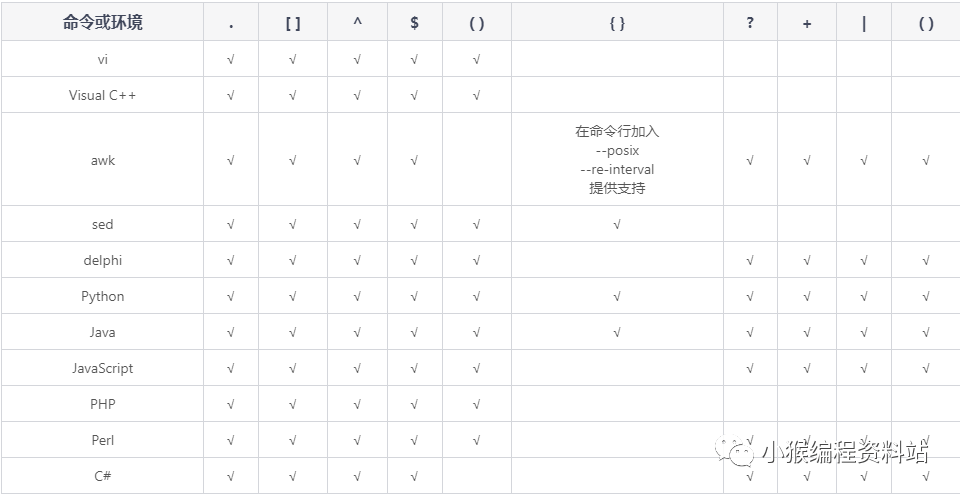
2W字正则表达式基础知识总结,这一篇就够了!!(含前端常用案例,建议收藏)
正则表达式 (Regular Expression,简称 RE 或 regexp ) 是一种文本模式,包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为"元字符")正则表达式使用单个字符串来描述、匹配一系列匹…...
自学web前端觉得好难,可能你遇到了这些困境
好多人跟我说上学的时候也学过前端,毕业了想从事web前端开发的工作,但自学起来好难,快要放弃了,所以我总结了一些大家遇到的困境,希望对你会有所帮助。 目录 1. 意志是否坚定 2. 没有找到合适自己的老师 3. 为了找…...

ASEMI中低压MOS管18N20参数,18N20封装,18N20尺寸
编辑-Z ASEMI中低压MOS管18N20参数: 型号:18N20 漏极-源极电压(VDS):200V 栅源电压(VGS):30V 漏极电流(ID):18A 功耗(PD&#x…...

[NetBackup]客户端安装后server无法连通client
client name处填写客户端主机名,server to use for backups and restores处填写server端名字,与hosts文件内保持一致;source client for restores处填写client主机名,与server端hosts文件中保持一致,与主机实际名称保持…...

黑马Java后端项目实战--在线聊天交友
【课程简介】 越来越多的系统都有消息推送的功能,如聊天室、邮件推送、系统消息推送等; 要实现消息推送就需要服务端在数据有变化时主动推送消息给客户端,本次课程将带大家使用websocket实现消息推送。 【主讲内容】 1.方法:如…...

【实战系列 2】Yapi接口管理平台Getshell-Linux后门权限维持与痕迹清除
文章目录 前言一、网站主页到Getshell二、SSH软链接后门三、Linux权限维持 --隐藏踪迹3.1 隐藏远程SSH登陆记录3.2、ssh软链接后门连接失败的原因以及解决办法3.3、隐藏踪迹-痕迹清楚3.3.1、隐藏历史操作命令3.3.2、隐藏文件/文件夹3.3.3、修改文件时间戳3.3.4、隐藏权限3.3.5、…...
设计模式之抽象工厂模式(C++)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 一、抽象工厂模式是什么? 抽象工厂模式是一种创建型的软件设计模式,该模式相当于升级版的工厂模式。 如果…...
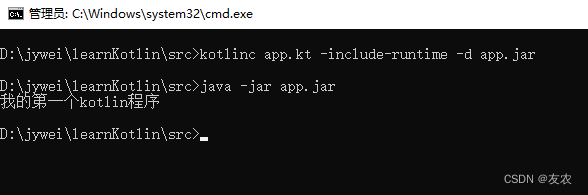
Kotlin新手教程一(Kotlin简介及环境搭建)
目录一、 什么是Kotlin?二、为什么要使用Kotlin?三、使用IntelliJ IDEA搭建Kotlin四、Kotlin使用命令行编译一、 什么是Kotlin? Kotlin 是一种在 Java 虚拟机上运行的静态类型编程语言,它也可以被编译成为 JavaScript 源代码&…...

【虚拟仿真】Unity3D打包WEBGL实现全屏切换
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 今天实现Unity3D打包WEBGL后实现按钮点击全屏和退出 全屏的实现…...

java对象内存结构分析与大小计算
java对象内存结构Java对象保存在堆中时,由三部分组成:对象头(object header):包括了关于堆对象的布局、类型、GC状态、同步状态和标识哈希码的基本信息。所有java对象都有一个共同的对象头格实例数据(Insta…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...