算法基础学习笔记——⑬高斯消元\组合计数\容斥原理
✨博主:命运之光
✨专栏:算法基础学习

目录
✨高斯消元
✨组合计数
🍓通过预处理逆元的方式求组合数:
🍓Lucas定理:
🍓分解质因数法求组合数:
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨高斯消元
高斯消元(Gaussian Elimination)是一种用于解线性方程组的算法,通过逐步的行变换来将方程组转化为简化的行阶梯形式,从而求解方程组的解。
🍓以下是一个用C语言编写的高斯消元算法的示例代码:
#include <stdio.h>
#define N 3 // 方程个数和未知数个数
void gaussianElimination(float matrix[N][N + 1], float solution[N]) {int i, j, k;float factor;// 前向消元for (i = 0; i < N - 1; i++) {for (k = i + 1; k < N; k++) {factor = matrix[k][i] / matrix[i][i];for (j = i; j < N + 1; j++) {matrix[k][j] -= factor * matrix[i][j];}}}// 回代求解for (i = N - 1; i >= 0; i--) {solution[i] = matrix[i][N];for (j = i + 1; j < N; j++) {solution[i] -= matrix[i][j] * solution[j];}solution[i] /= matrix[i][i];}
}
int main() {float matrix[N][N + 1];float solution[N];int i, j;printf("Enter the augmented matrix:\n");for (i = 0; i < N; i++) {for (j = 0; j < N + 1; j++) {scanf("%f", &matrix[i][j]);}}gaussianElimination(matrix, solution);printf("Solution:\n");for (i = 0; i < N; i++) {printf("x%d = %.2f\n", i + 1, solution[i]);}return 0;
}在上述代码中,我们定义了gaussianElimination函数来执行高斯消元算法。算法分为两个阶段:前向消元和回代求解。
前向消元阶段通过循环进行逐行消元操作,将方程组转化为行阶梯形式。首先,通过除以主对角线上的元素将当前行的主元素变为1。然后,通过逐行减去当前行的倍数,将当前列下方的元素变为0。
回代求解阶段从最后一行开始,通过回代计算未知数的值。首先,将当前行的右侧常数项赋值给对应的未知数。然后,逐列减去已知未知数的乘积,最后除以当前行的主元素。
在main函数中,我们首先接受用户输入的增广矩阵,其中最后一列为常数项。然后,调用gaussianElimination函数来解方程组,并将结果打印出来。
你可以运行上述代码,根据提示输入增广矩阵,程序将计算并输出方程组的解。









🍓高斯消元 :
// a[N][N]是增广矩阵
int gauss()
{int c, r;for (c = 0, r = 0; c < n; c ++ ){int t = r;for (int i = r; i < n; i ++ ) // 找到绝对值最大的行if (fabs(a[i][c]) > fabs(a[t][c]))t = i;if (fabs(a[t][c]) < eps) continue;for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0if (fabs(a[i][c]) > eps)for (int j = n; j >= c; j -- )a[i][j] -= a[r][j] * a[i][c];r ++ ;}if (r < n){for (int i = r; i < n; i ++ )if (fabs(a[i][n]) > eps)return 2; // 无解return 1; // 有无穷多组解}for (int i = n - 1; i >= 0; i -- )for (int j = i + 1; j < n; j ++ )a[i][n] -= a[i][j] * a[j][n];return 0; // 有唯一解
}✨组合计数
在C语言中,可以使用动态规划来实现组合计数(Combination Counting)。组合计数用于计算从n个元素中选择k个元素的组合数。
🍓以下是一个用C语言编写的组合计数算法的示例代码:
#include <stdio.h>
// 计算组合数C(n, k)
int combinationCount(int n, int k) {int C[n + 1][k + 1];int i, j;// 基本情况for (i = 0; i <= n; i++) {for (j = 0; j <= i && j <= k; j++) {if (j == 0 || j == i)C[i][j] = 1;elseC[i][j] = C[i - 1][j - 1] + C[i - 1][j];}}return C[n][k];
}
int main() {int n, k;printf("Enter the values of n and k: ");scanf("%d %d", &n, &k);int result = combinationCount(n, k);printf("Combination Count: %d\n", result);return 0;
}在上述代码中,我们定义了一个combinationCount函数来计算组合数C(n, k)。算法使用动态规划的思想,使用一个二维数组C来存储中间结果。
首先,我们处理基本情况,即当k等于0或k等于n时,组合数C(n, k)为1。然后,通过递推关系C(n, k) = C(n-1, k-1) + C(n-1, k),我们填充C数组的其余元素。
在main函数中,我们接受用户输入的n和k的值,并调用combinationCount函数来计算组合数。然后,我们输出计算结果。
你可以运行上述代码,根据提示输入n和k的值,程序将计算并输出组合数C(n, k)的结果。
请注意,上述代码中的组合计数算法使用了动态规划的方法,对于较大的n和k可能会产生较大的中间结果。在实际应用中,可以使用更高效的算法或数学公式来计算组合数。

🍓递推法求组合数:
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )for (int j = 0; j <= i; j ++ )if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
🍓通过预处理逆元的方式求组合数:
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
int qmi(int a, int k, int p) // 快速幂模板
{int res = 1;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}


🍓Lucas定理:
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
int qmi(int a, int k, int p) // 快速幂模板
{int res = 1 % p;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}
int C(int a, int b, int p) // 通过定理求组合数C(a, b)
{if (a < b) return 0;LL x = 1, y = 1; // x是分子,y是分母for (int i = a, j = 1; j <= b; i --, j ++ ){x = (LL)x * i % p;y = (LL) y * j % p;}return x * (LL)qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p)
{if (a < p && b < p) return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

🍓分解质因数法求组合数:
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
3. 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
void get_primes(int n) // 线性筛法求素数
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}
int get(int n, int p) // 求n!中的次数
{int res = 0;while (n){res += n / p;n /= p;}return res;
}
vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板
{vector<int> c;int t = 0;for (int i = 0; i < a.size(); i ++ ){t += a[i] * b;c.push_back(t % 10);t /= 10;}while (t){c.push_back(t % 10);t /= 10;}return c;
}
get_primes(a); // 预处理范围内的所有质数
for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数
{int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘for (int j = 0; j < sum[i]; j ++ )res = mul(res, primes[i]);



✨容斥原理
在C语言中,可以使用容斥原理(Inclusion-Exclusion Principle)来解决一些计数问题。容斥原理是组合数学中的一个重要原理,用于计算多个集合的并集、交集等情况下的计数问题。
🍓以下是一个用C语言编写的容斥原理算法的示例代码:
#include <stdio.h>// 计算集合交集的大小
int intersectionSize(int set[], int setSize) {int result = set[0];for (int i = 1; i < setSize; i++) {result &= set[i];}return result;
}// 计算集合并集的大小
int unionSize(int set[], int setSize) {int result = set[0];for (int i = 1; i < setSize; i++) {result |= set[i];}return result;
}// 计算容斥原理的应用
int inclusionExclusion(int sets[][3], int numSets, int setSize) {int result = 0;for (int i = 1; i < (1 << numSets); i++) {int sign = (__builtin_popcount(i) % 2 == 1) ? 1 : -1;int tempSet[setSize];for (int j = 0; j < setSize; j++) {tempSet[j] = 0;}for (int j = 0; j < numSets; j++) {if (i & (1 << j)) {for (int k = 0; k < setSize; k++) {tempSet[k] |= sets[j][k];}}}int intersection = intersectionSize(tempSet, setSize);result += sign * intersection;}return result;
}int main() {int sets[3][3] = {{1, 2, 3},{2, 3, 4},{3, 4, 5}};int numSets = 3;int setSize = 3;int result = inclusionExclusion(sets, numSets, setSize);printf("Result: %d\n", result);return 0;
}在上述代码中,我们定义了三个函数:intersectionSize用于计算集合交集的大小,unionSize用于计算集合并集的大小,inclusionExclusion用于应用容斥原理。
intersectionSize函数通过遍历集合元素并执行按位与操作来计算集合交集的大小。
unionSize函数通过遍历集合元素并执行按位或操作来计算集合并集的大小。
inclusionExclusion函数使用位运算和循环来实现容斥原理的应用。它从空集开始,遍历所有子集,并计算交集的大小。根据子集中元素的数量的奇偶性,确定交集的贡献正负号,并累加到最终结果中。
在main函数中,我们定义了一个包含三个集合的二维数组,并调用inclusionExclusion函数来应用容斥原理计算结果。
你可以运行上述代码,它将输出应用容斥原



相关文章:

算法基础学习笔记——⑬高斯消元\组合计数\容斥原理
✨博主:命运之光 ✨专栏:算法基础学习 目录 ✨高斯消元 ✨组合计数 🍓通过预处理逆元的方式求组合数: 🍓Lucas定理: 🍓分解质因数法求组合数: 前言:算法学习笔记记录日常分享,需…...
渗透测试辅助工具箱
0x01 说明 渗透测试辅助工具箱 运行条件:jdk8 双击即可运行 反弹shell,命令生成器,自动编码,输入对应IP端口即可,实现一劳永逸,集成一些小工具,辅助渗透,提高效率 输入框说明 L…...

chatgpt赋能python:Python后退命令:如何让你的程序退回到之前的状态
Python后退命令:如何让你的程序退回到之前的状态 Python是一种高级编程语言,因其易读易懂而闻名于世。Python中有很多命令用于编写程序,其中一项重要的命令是后退命令。本文将介绍Python后退命令的使用方法,并为您提供详细的步骤…...

OJ练习第127题——统计范围内的元音字符串数
统计范围内的元音字符串数 力扣链接:2559. 统计范围内的元音字符串数 题目描述 给你一个下标从 0 开始的字符串数组 words 以及一个二维整数数组 queries 。 每个查询 queries[i] [li, ri] 会要求我们统计在 words 中下标在 li 到 ri 范围内(包含 这…...
图片优化: CssSprites与Base64编码
文章目录 1 css sprites1.1 CSS Sprites是什么1.2 为什么需要css sprites1.3 优势1.4 使用原理1.5 DEMO 2 图片Base64编码 1 css sprites 1.1 CSS Sprites是什么 CSS Sprites是一种网页图片应用处理方式。 又被解释为: CSS精灵CSS图像拼合CSS贴图定位CSS图片精灵…...

JavaScript中的Map、WeakMap和Object的区别
Map Map是一种新的数据结构,它允许使用任何数据类型(包括对象和基本数据类型)作为键。 Map的一些特性包括: 保持键的插入顺序:当遍历Map时,键值对会按照插入顺序返回。键可以是任意类型:与Obj…...

华为OD机试之打印机队列(Java源码)
打印机队列 题目描述 有5台打印机打印文件,每台打印机有自己的待打印队列。 因为打印的文件内容有轻重缓急之分,所以队列中的文件有1~10不同的代先级,其中 数字越大优先级越高 打印机会从自己的待打印队列中选择优先级最高的文件来打印。 如…...

分享一个国内免费的ChatGPT网站,手机电脑通用,免费无限制,支持AI绘画
背景 ChatGPT作为一种基于人工智能技术的自然语言处理工具,近期的热度直接沸腾🌋。 作为一个AI爱好者,翻遍了各大基于ChatGPT的网站,终于找到一个免费!免登陆!手机电脑通用!国内可直接对话的C…...

【面向对象编程1】——类和对象——如桃花来
目录索引 面向过程和面向对象的区别:面向过程:面向对象:总结: 类和对象:定义类:语法: 创建对象:实例演示: 魔法方法:__init __方法:__ del __方法…...
chat聊天系统消息消费时遇到的问题及优化思路(二)
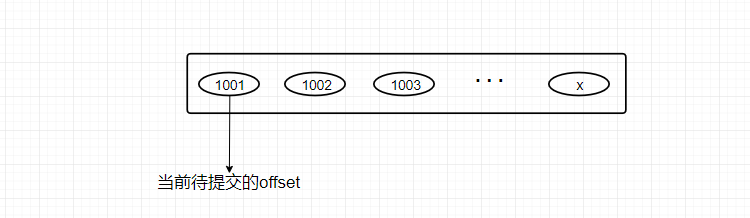
1、前言 考虑下面几个条件下如何提升kafka的消费速度 消息要求严格有序,如chat聊天消息业务处理速度慢,如处理一条数据需要100ms分片不合理,如有的分区很闲,有的分区消息数量积压 2、解决方案 1、顺序问题 关于消息消费时存在…...

js正则中的match()
在前端开发中,正则表达式是一大利器。所以我们这次就来讨论下match()方法。 match本身是JavaScript语言中字符串对象的一个方法,该方法的签名是 match([string] | [RegExp]) 它的参数既可以是一个字符串,也可以是一个正则表达式。该方法绝…...
Apache 配置和应用
目录 构建虚拟 Web 主机 Options指令解释 Options指令常用选项 AllowOverride指令解释: 地址限制策略: httpd服务支持的虚拟主机类型包括以下三种: 基于域名的虚拟主机 1.为虚拟主机提供域名解析 2.为虚拟主机准备网页文档 3.添加虚拟…...

实现PyTorch/ONNX自定义节点操作的TensorRT部署
参考一 下面是基本步骤: 加载训练好的bev transformer网络权重参数: import torch from model import Modelmodel Model() model.load_state_dict(torch.load("path/to/weights"))定义新的自定义操作: import torch from torc…...

Shamir 秘密共享、GMW和BGW方案
一、Shamir秘密共享 Shamir秘密共享方案是一种将秘密拆分成多份并分配给多个参与者保存,只有在满足特定条件下才能恢复原始秘密的密码学方案。它具有良好的容错性、加法同态性和无条件安全性等特点。 具体地,Shamir秘密共享方案可以概括为以下步骤&…...

Day56【动态规划】583.两个字符串的删除操作、72.编辑距离
583.两个字符串的删除操作 力扣题目链接/文章讲解 视频讲解 1、确定 dp 数组下标及值含义 dp[i][j]:以下标 i 为结尾的字符串 word1,和以下标 j 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j] 2、…...

Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现…...
ASP.NET Core
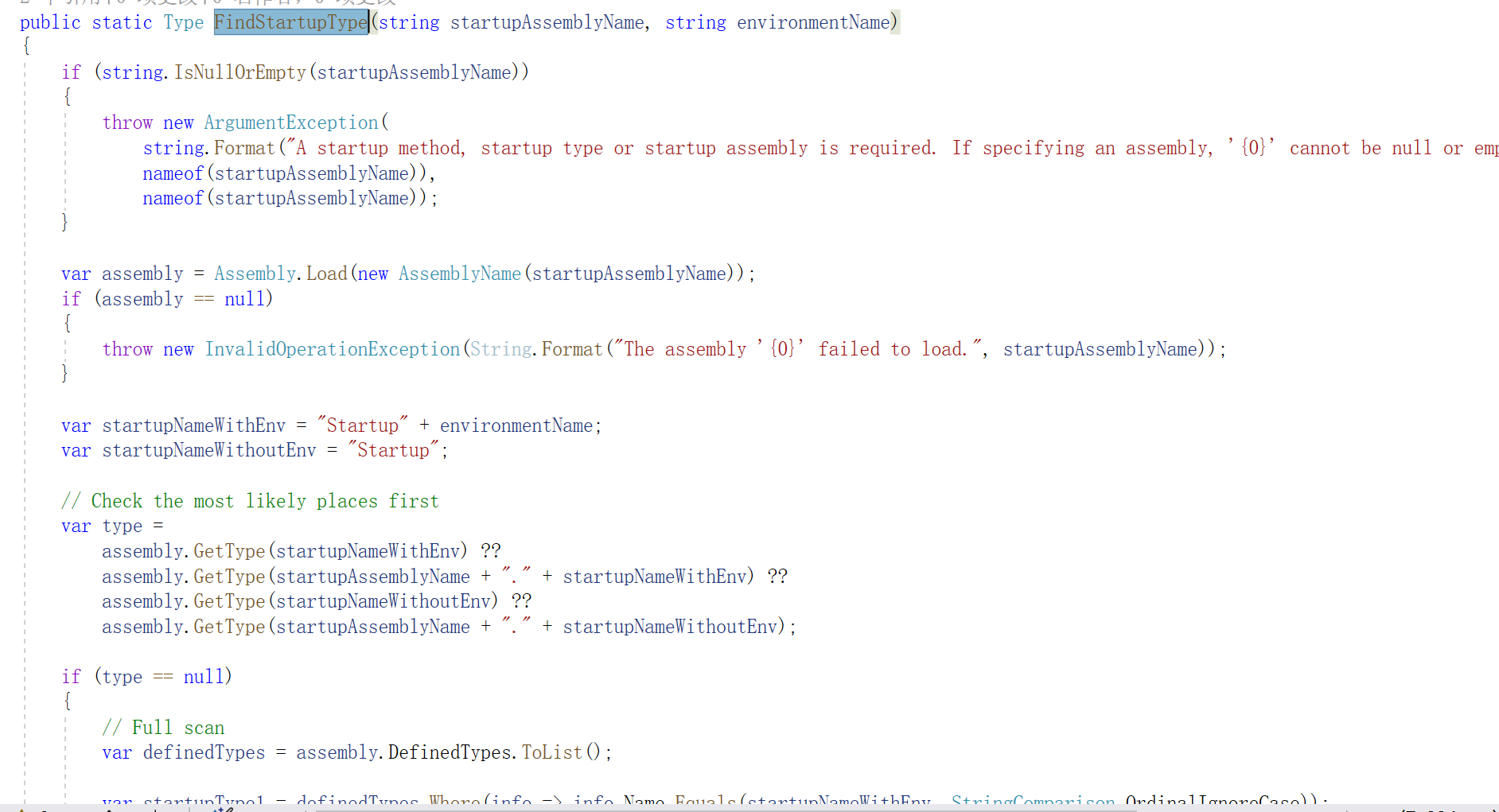
1. 入口文件 一个应用程序总有一个入口文件,是应用启动代码开始执行的地方,这里往往也会涉及到应用的各种配置。当我们接触到一个新框架的时候,可以从入口文件入手,了解入口文件,能够帮助我们更好地理解应用的相关配置…...
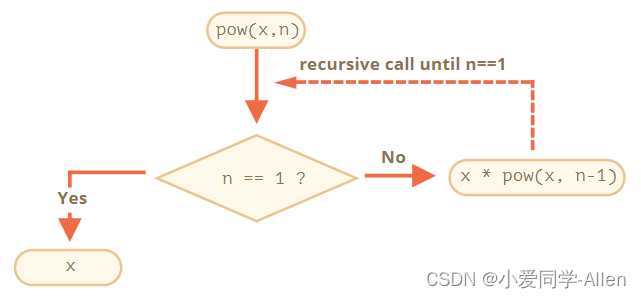
javascript基础二十二:举例说明你对尾递归的理解,有哪些应用场景
一、递归 递归(英语:Recursion) 在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 其核心思想是把一个大型…...
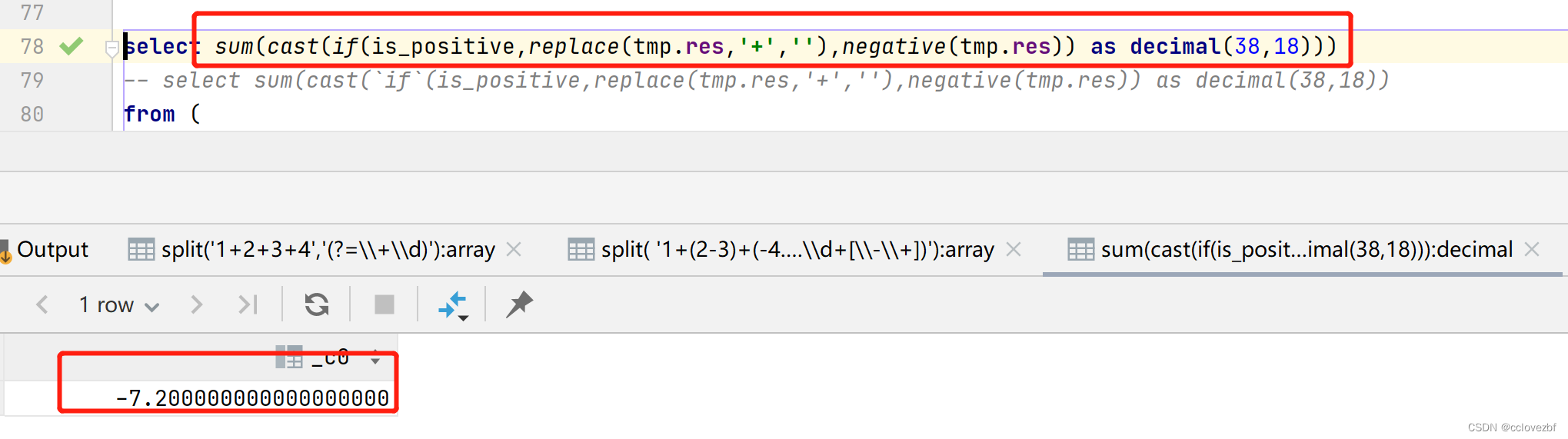
hive中如何计算字符串中表达式
比如 select 1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 col ,1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 result \ 现在的需求式 给你一个字符串如上述col 你要算出result。 前提式 只有和-的运算,而且只有嵌套一次 -(4-3)没有 -(-4(3-(31)))嵌套多次。 第一步我们需要将运…...

如何将maven项目改为springboot项目?
将 Maven 项目转换为 Spring Boot 项目需要进行以下步骤: 1. 在 Maven 项目中添加 Spring Boot 的依赖。可以通过在 pom.xml 文件中添加以下依赖来实现: <dependency> <groupId>org.springframework.boot</groupId> <artifactId>…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
