最优化理论-KKT定理的推导与实现
目录
一、引言
二、最优化问题的基本概念
三、KKT条件的引入
1. 梯度条件
2. 原始可行性条件
3. 对偶可行性条件
四、KKT定理的表述
五、KKT定理的证明
1. 构造拉格朗日函数
2. 构造拉格朗日对偶函数
3. 推导KKT条件
4. 解释KKT条件
六、KKT定理的应用
七、总结
一、引言
最优化问题是数学中的一个重要分支,它研究如何在一定的限制条件下,寻找使某个目标函数取得最大或最小值的变量取值。最优化问题在实际应用中有着广泛的应用,例如在经济学、工程学、管理学等领域中都有着重要的应用。最优化问题的研究不仅可以帮助我们更好地理解现实世界中的问题,还可以为我们提供有效的解决方案。
在最优化问题中,KKT定理是一个非常重要的理论工具。KKT定理是最优化问题中的一个必要条件,它可以帮助我们判断一个解是否为最优解,并且可以为我们提供求解最优解的方法。本文将介绍最优化理论中的KKT定理,包括其定义、表述、证明和应用。
二、最优化问题的基本概念
在介绍KKT定理之前,我们需要先了解最优化问题的基本概念。最优化问题通常可以表示为以下形式:
其中,是一个
维向量,
是一个实值函数,称为目标函数;
和
是一些实值函数,称为约束条件。我们称上述问题为一个约束优化问题。
在约束优化问题中,我们需要找到一个满足所有约束条件的,使得
取得最小值。这个
就是我们所要求解的最优解。但是,在实际问题中,我们往往很难直接求解出最优解,因此需要借助一些数学工具来帮助我们求解。
三、KKT条件的引入
在介绍KKT定理之前,我们需要先引入KKT条件。KKT条件是一组必要条件,它可以帮助我们判断一个解是否为最优解。KKT条件包括以下三个部分:
1. 梯度条件
其中,是最优解,
和
是拉格朗日乘子。
2. 原始可行性条件
3. 对偶可行性条件
KKT条件是最优化问题中的一个必要条件,它可以帮助我们判断一个解是否为最优解。但是,KKT条件并不是充分条件,即满足KKT条件的解不一定是最优解。因此,我们需要引入KKT定理来判断一个解是否为最优解。
四、KKT定理的表述
KKT定理是最优化问题中的一个重要理论工具,它可以帮助我们判断一个解是否为最优解,并且可以为我们提供求解最优解的方法。KKT定理的表述如下:
设是一个约束优化问题的局部最优解,且满足原始可行性条件和对偶可行性条件,则存在一组拉格朗日乘子
和
,使得梯度条件成立。
KKT定理告诉我们,如果一个解满足原始可行性条件和对偶可行性条件,那么它一定满足梯度条件。因此,我们可以通过检验梯度条件来判断一个解是否为最优解。
五、KKT定理的证明
KKT定理的证明需要用到拉格朗日对偶性,具体证明过程可以分为以下几步:
1. 构造拉格朗日函数
首先,我们需要构造一个拉格朗日函数,它包含了原问题的约束条件和目标函数。具体地,对于原问题:
我们可以构造如下的拉格朗日函数:
其中, 和
是拉格朗日乘子,它们的取值可以通过对拉格朗日函数求导并令其为零来确定。
2. 构造拉格朗日对偶函数
接下来,我们需要构造拉格朗日对偶函数。具体地,我们将拉格朗日函数对 求最小值,得到:
注意到, 是一个凸函数,因此
也是一个凸函数。
3. 推导KKT条件
根据拉格朗日对偶性,我们有:
因此,我们可以得到以下的KKT条件:
其中,、
和
是拉格朗日函数的最优解。
4. 解释KKT条件
KKT条件告诉我们,如果一个点 是原问题的最优解,那么存在拉格朗日乘子
和
,满足上述条件。这些条件告诉我们,最优解
必须满足原问题的约束条件,同时,拉格朗日乘子
和
可以帮助我们判断约束条件是否被严格满足。
六、KKT定理的应用
KKT定理可以应用于各种最优化问题,包括线性规划、二次规划、非线性规划等。具体地,我们可以使用KKT条件来判断一个点是否是最优解,或者使用KKT条件来求解最优解。
下面是使用MATLAB实现KKT算法的步骤:
1. 定义优化问题的目标函数和约束条件。
2. 使用MATLAB的优化工具箱中的函数创建一个优化问题对象。
3. 使用KKT条件来求解优化问题。KKT条件是一组必要条件,用于判断一个点是否是最优解。在MATLAB中,可以使用fmincon函数来求解带有约束条件的优化问题,并使用输出参数来检查KKT条件是否满足。
下面是一个简单的例子,演示如何使用MATLAB实现KKT算法:
% 定义目标函数和约束条件
fun = @(x) x(1)^2 + x(2)^2; % 目标函数
nonlcon = @(x) [x(1) + x(2) - 1, x(1) - x(2) - 1]; % 约束条件% 创建优化问题对象
problem = struct();
problem.objective = fun;
problem.x0 = [0, 0];
problem.nonlcon = nonlcon;% 使用fmincon函数求解优化问题
[x, fval, exitflag, output, lambda] = fmincon(problem);% 检查KKT条件是否满足
grad = [2*x(1), 2*x(2)]; % 目标函数的梯度
c = nonlcon(x); % 约束条件的值
ceq = c(1); % 等式约束条件的值
cineq = c(2); % 不等式约束条件的值
lambda_eq = lambda.eqlin; % 等式约束条件的拉格朗日乘子
lambda_ineq = lambda.ineqlin; % 不等式约束条件的拉格朗日乘子
kkt1 = grad + lambda_eq*nonlcon(x)'; % KKT条件1
kkt2 = lambda_ineq; % KKT条件2
kkt3 = cineq; % KKT条件3if norm(kkt1) < 1e-6 && norm(kkt2) < 1e-6 && norm(kkt3) < 1e-6disp('KKT条件满足');
elsedisp('KKT条件不满足');
end在上面的例子中,我们定义了一个目标函数和两个约束条件。然后,我们使用MATLAB的优化工具箱中的函数创建一个优化问题对象,并使用fmincon函数求解该问题。最后,我们检查KKT条件是否满足。如果KKT条件满足,则说明我们找到了最优解。
七、总结
KKT定理是最优化理论中的重要定理,它告诉我们如何判断一个点是否是最优解,以及如何求解最优解。KKT定理的证明需要用到拉格朗日对偶性,具体证明过程可以分为构造拉格朗日函数、构造拉格朗日对偶函数、推导KKT条件和解释KKT条件四个步骤。
相关文章:
最优化理论-KKT定理的推导与实现
目录 一、引言 二、最优化问题的基本概念 三、KKT条件的引入 1. 梯度条件 2. 原始可行性条件 3. 对偶可行性条件 四、KKT定理的表述 五、KKT定理的证明 1. 构造拉格朗日函数 2. 构造拉格朗日对偶函数 3. 推导KKT条件 4. 解释KKT条件 六、KKT定理的应用 七、总结 …...

chatgpt赋能python:Python中引入其他包的指南
Python中引入其他包的指南 Python是一种流行的编程语言,拥有丰富的开源软件包和库。许多Python程序将使用其他包来增强其功能。在本文中,我们将探讨如何在Python项目中使用和引入其他包。 什么是Python包和库? Python包是一组可重复使用的…...

设计模式-组合模式
应用场景 实现规则匹配的逻辑 比如> <,同时支持 and or 多个条件组合 新增一个条件就增加一个实现类 说明 对于这种需要实现规则匹配的逻辑,可以考虑使用策略模式。策略模式可以将不同的算法封装成不同的策略类,让它们可以相互替换,…...
DMBOK知识梳理for CDGA/CDGP——第四章 数据架构(附常考知识点)
关 注ghz“大数据食铁兽”,回复“知识点”获取《DMBOK知识梳理for CDGA/CDGP》常考知识点(第四章 数据架构) 第四章 数据架构 第四章是CDGA|CDGP考试的重点考核章节之一,分值占比高,知识点比较密集,重点…...

MyBatisPlus总结(1.0)
MyBatis-Plus MyBatis-Plus介绍 MyBatis-Plus(简称MP)是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生 特性 无侵入:只做增强不做改变,引入它不会对现有工程产生影…...

职场老油条表示真干不过,部门新来的00后测试员已把我卷崩溃,想离职了...
在程序员职场上,什么样的人最让人反感呢? 是技术不好的人吗?并不是。技术不好的同事,我们可以帮他。 是技术太强的人吗?也不是。技术很强的同事,可遇不可求,向他学习还来不及呢。 真正让人反感的,是技术平平&#x…...

【每日挠头算法题(1)】——旋转字符串|亲密字符串
文章目录 一、旋转字符串思路1思路2 二、亲密字符串思路 总结 一、旋转字符串 点我直达终点~ 思路1 前提:如果s串和goal串长度不等,则goal串不可能是s串旋转得来,直接返回false; 通过观察,可以发现每旋转一次&#…...

什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens,ChatGPT里面的Tokens如何计数? 什么是 tokens? Tokens 可以被认为是词语的片段。在 API 处理提示之前,输入会被分解成 tokens。这些 tokens 并不会精确地在单词的开始或结束处切分 - tokens 可以包含尾随的空格甚…...
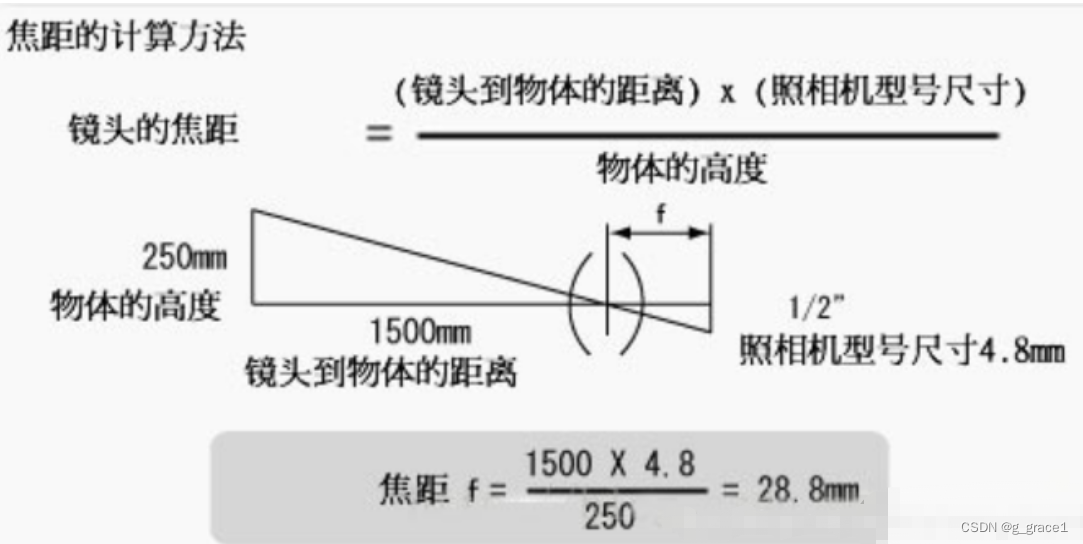
工业镜头分类、相关参数含义
一、工业镜头参数 1、焦距/后焦距 焦距是像方主面到像方焦点的距离。后焦距指光线离开镜头最后一片镜片表面到sensor感光面的距离,如8mm,16mm,25mm等; 焦距的大小决定着视角大小,焦距数值小,视角大&#…...
)
码蹄杯语言基础:数组(C语言)
码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist ⭐MT1381逆序输出数组 定义一个长度为10的整型数组,输入10个数组元素的值,然后逆序输出他们 格式 输入格式: 输入10个数组元素的值,整型,空…...

DJ4-2 程序的装入和链接
目录 4.2.1 程序的装入 一、绝对装入方式 二 、可重定位装入方式 三、动态运行时装入方式 4.2.2 程序的链接 一、静态链接 二、装入时动态链接 三、运行时动态链接 在多道程序环境下,如果程序要运行,那么必须为之创建进程。而创建进程的第一件…...

开源项目合集....
likeshop开源商城系统,公众号商城、H5商城、微信小程序商城、抖音小程序商城、字节小程序商城、头条小程序商城、安卓App商城、苹果App商城代码全开源,免费商用。 适用场景:B2C商城、新零售商城、社交电商商城、分销系统商城、小程序商城、商…...
机器学习 | 降维问题
目录 一、主成分分析 二、奇异值分解 2.1 奇异值分解原理 2.2 奇异值分解实践 三、特征值与特征向量 一、主成分分析 主成分有如下特征: 每个主成分是原变量的线性组合;各个主成分之间互不相关;主成分按照方差贡献率从大到小依次排列&…...
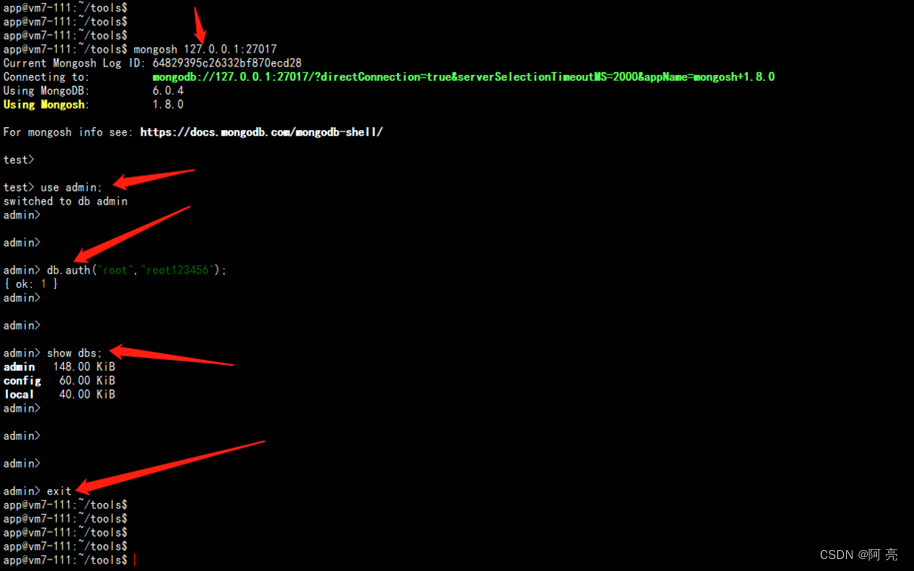
Ubuntu20.04平台下使用二进制包部署MongoDB-6.0.4单实例
文章目录 1.1 准备服务器的基本信息1.2 操作系统上创建其用户1.3 部署MongoDB服务端1.4 部署MongoDB客户端1.5 部署MongoDB 27017实例1.5.1 创建相关目录1.5.2 准备配置文件1.5.3 准备启停脚本1.5.4 进行启停测试1.5.5 加入开机自启动 1.6 创建超级管理员用户1.6.1 创建本地的超…...
Snipaste工具推荐
Snipaste Snipaste 不只是截图,善用贴图功能将帮助你提升工作效率! 新用户? 截图默认为 F1,贴图为 F3,然后请对照着 快捷键列表 按一遍,体会它们的用法,就入门啦! 遇到了麻烦&…...
MinIO快速入门——在Linux系统上安装和启动
1、简介 MinIO 是一款基于Go语言发开的高性能、分布式的对象存储系统。客户端支持Java,Net,Python,Javacript, Golang语言。MinIO系统,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 2、环境搭建&#…...
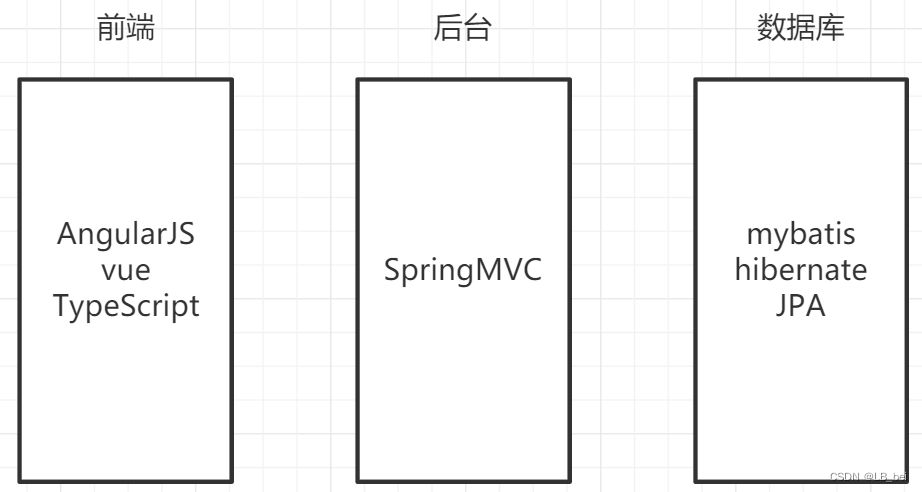
07.JavaWeb-Vue+elementUI
1.Vue 功能替代JavaScript和jQuery,基于JavaScript实现的前端框架 1.1配置Vue 1.1.1引入vue库 方法一:通过cdn链接引入最新版本的vue(可能会慢些) <head><script src"https://cdn.jsdelivr.net/npm/vue">…...
经典面试题---【第一档】
1.如果你想new一个Quene,你有几种方式?他们之间的区别是什么? 2.Redis 是如何判断数据是否过期的呢? Redis 通过一个叫做过期字典(可以看作是 hash 表)来保存数据过期的时间。过期字典的键指向 Redis 数据…...

欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)正式启动,开启报名通道
6月8日,欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)启动仪式暨北京推介会圆满举行。活动由欧美同学会(中国留学人员联谊会)主办,中共浙江省委统战部支持,浙江省欧美同学会、中…...

python3 爬虫相关学习8:python 的常见报错内容 汇总收集
目录 1 拼写错误 AttributeError: NameError: 等等 2 类型错误 TypeError: 如字符串连接错误 TypeError: can only concatenate str (not “int“) to str 3 意外缩进 IndentationError: unexpected indent 4 找不到对应模块 ModuleNotFoundError: 5 语法错误 Syntax…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
