MIT6.024学习笔记(二)——图论(1)
学习不是为了竞争和战胜他人,而是为了更好地了解自己和世界。 - 达赖喇嘛
文章目录
- 图的相关概念
- 涂色问题
- 基础涂色方法(贪婪算法)
- 证明
- 二分图
- 匹配问题
- 应用:稳定婚烟问题
- 算法
- 性质及其证明
图的相关概念
- 图的定义:一组(V,E)对。
- V:一个点集的集合。
- E:边集,呈现形式为V上的一个关系。什么是关系
V的一个例子为{x1,x2,x3},E的一个例子为{(x1,x2),(x2,x3)},也可写成{x1-x2,x2-x3}。
- 相邻点:如果两个点之间有边,那么这两个点就是相邻的。
- 映射:如果(x1,x2)是E的一个元素,那么E映射到x1,E也映射到x2。
- 度数:边集映射到x1的次数称为x1的度数。
- 环:起点和终点都是同一个点的边称为环。
- 重边:两个起点和终点完全相同的边称为重边。
- 简单图:没有环或者重边的图称作简单图。
涂色问题
给定一个图,如果最少能用K种颜色为图涂色,使相邻点拥有不同颜色,那么K称为该图的色度。
基础涂色方法(贪婪算法)
步骤:
- 将点标号为x1,x2,…,xn。
- 将颜色标号为c1,c2,…,cn。
- 每次用标号最小的合法颜色涂标号最小的尚未上色的点。
易证:使用这种算法,如果图中度数最多的点有d度,那么最多使用(d+1)种颜色。
证明
可以用归纳法证明,设Pn表示有n个点的图满足命题:
- 基础步骤:n=1时,d=0,用一种颜色,P1=T。
- 归纳步骤:假设Pn=T,考虑有(n+1)个点的图,该图中的点最多拥有d度。若在该图中取走一个点,那么剩下的n点图中的点也最多拥有d度且一定满足Pn。再加回该点,即使该点拥有d度,且相连的d个点颜色都不同,该点也可以使用第(d+1)种颜色,因此(n+1)点图的色度<=(d
+1),Pn+1=T。□
二分图
如果一个图可以分成左右两个集合,集合内部的点都不相邻,分属于两个集合的部分点有相邻关系,那么这个图称为二分图。不难看出,二分图色度为2。
匹配问题
- 匹配:给定一个图,这个图的一个所有点都有且只有1度的子图称作该图的一个匹配。例如:
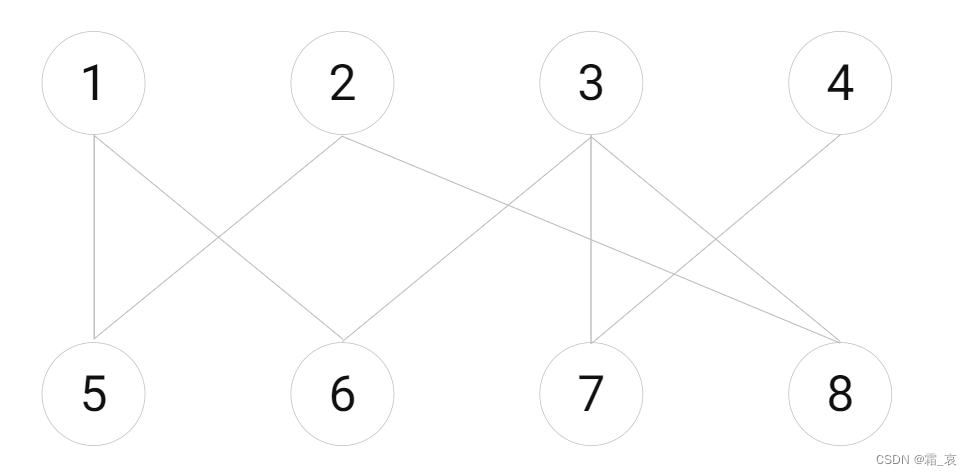
对于这个图,{x1-x5,x2-x8,x3-x6,x4-x7}是该图的一个匹配。注意,{x1-x5}也是该图的一个匹配。
- 如果一个匹配包括原图的所有点,那么这个匹配是一个完美匹配。
- 对于带权图来说,一个匹配的权重是匹配中所有边的权重之和。此时完美匹配需满足两个条件:包括所有点且该匹配拥有最小权重。我们也称此时的完美匹配为最小权重匹配。
应用:稳定婚烟问题
看下面的图,假定A,B是男生,C,D是女生。边的权重值越小,代表该男生、女生越喜欢ta的该相邻点:
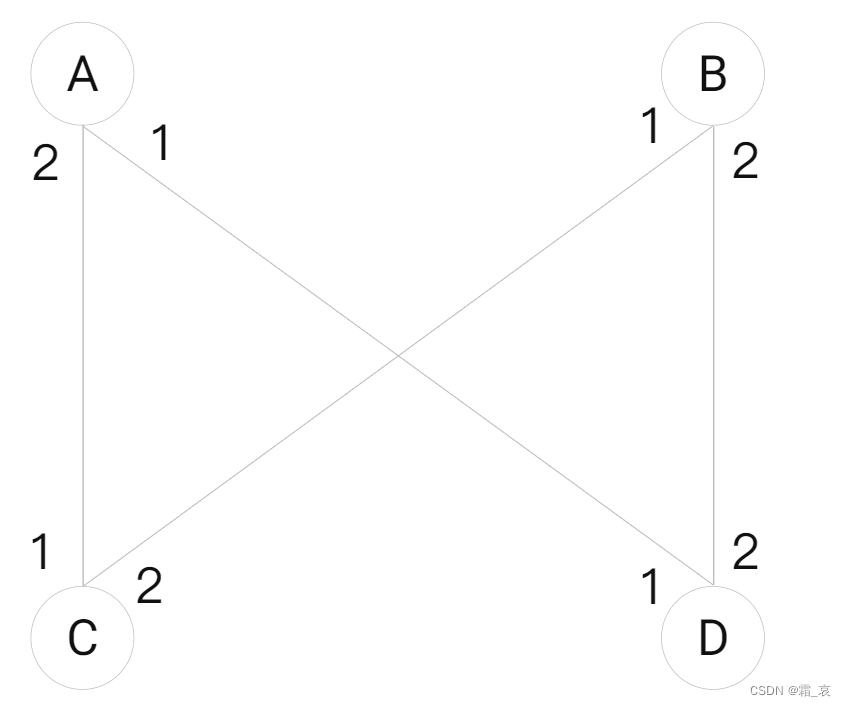
我们可以看出A更喜欢D,B更喜欢C…假定如果A和C结婚,B和D结婚,那么比起伴侣,A和D都更喜欢对方,那么他们可能发生出轨行为,导致婚烟不稳定。反之,如果A和D结婚,B和C结婚,那么婚烟是稳定的,因为即使C更喜欢A,但A更喜欢他的伴侣D,因此他不愿意和C出轨。
那么,对于一个带权图,怎么找到它的稳定婚烟匹配呢?
算法
首先明确一点:只有二分图才有稳定婚烟匹配,因此如果混入了gay或……那么不存在稳定婚烟匹配。另外,男女生数量必须相同,这点很好理解。我们可以通过一个称作TMA的算法找到一个图的一种稳定婚烟匹配。TMA步骤如下:
- 每个男生去找他最喜欢的女生示爱。
- 如果女生发现有多个男生来找她,她查看自己的权重并找到她最喜欢的,拒绝其他男生。注意这并不代表留下的这个男生就是她的最终伴侣。
- 被拒绝的男生将这个女生从他的权重名单里划掉,然后顺位去找下一个女生示爱。
- 重复第二步和第三步,直到每个女生面前有且只有一位男生示爱,算法结束,找到稳定婚烟匹配。
举个例子说明。假定对于每个男生和女生,他们的权重名单如下(这里跳过图阶段而直接抽象出信息),最左边的是最喜欢的,最右边的是最不喜欢的:

-
男生按照权重名单去找相对应的女生。
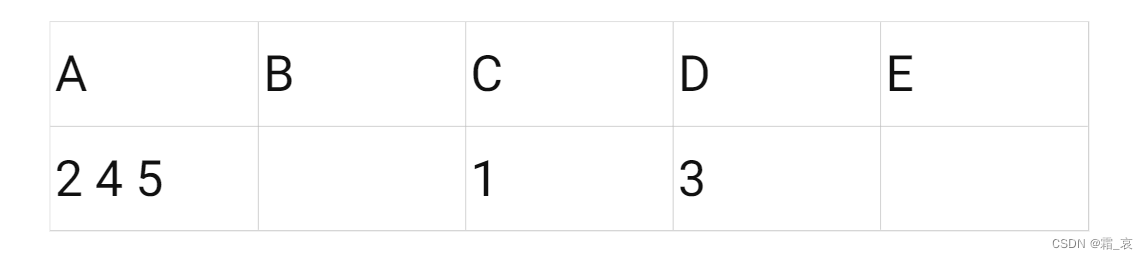
-
在A面前有三个男生,根据名单,她留下5;剩下的2 4两男生划掉A,分别去找下一个女生:
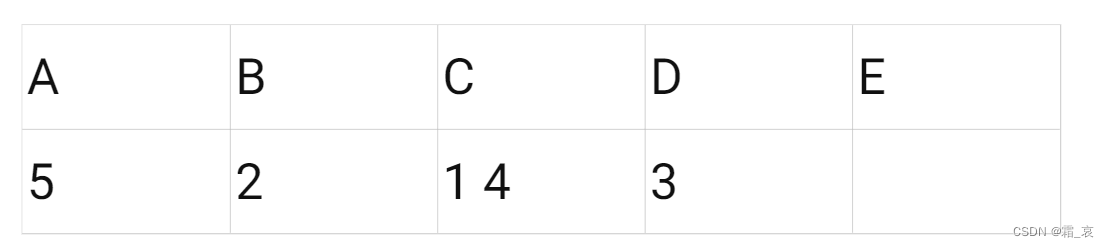
-
C查看名单,留下4;1划掉C,去找B:
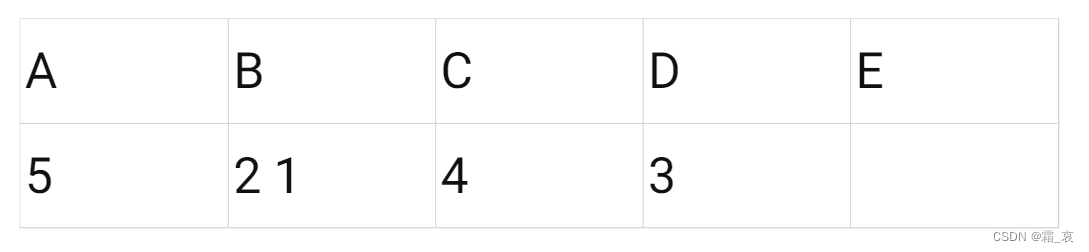
-
B查看名单,留下2;1划掉B,去找E:
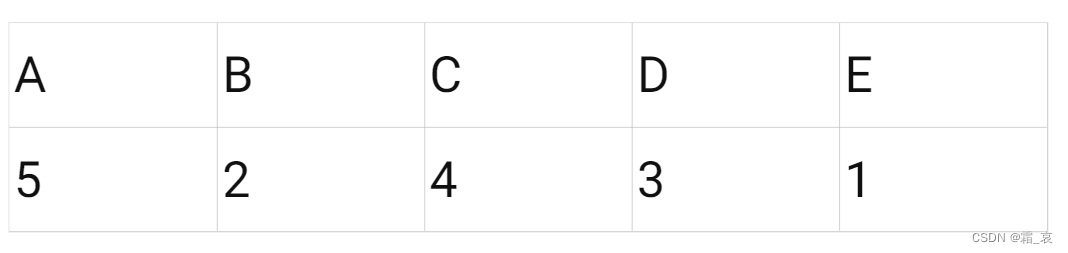
至此,所有女生面前有且仅有一个男生,算法结束。
经过检验(感兴趣的读者可以自行尝试一下),这个算法是有效的。接下来我们对其性质进行证明。
性质及其证明
- 性质1:这个算法会在不多于(n2+1)个周期内结束。这个性质很好理解,n个男生,n个女生,男生的名单最多划n2次,除了第一个回合外,每个回合至少有一个男生的名单会被划,因此算法最多执行(n2+1)个周期。
- 性质2:如果一个女生拒绝了一个男生,那么从她拒绝的那一天开始到算法结束,她身边一定有一个她更喜欢的示爱者。这个性质可以用归纳法来形式化的证明,但直观上也很好理解,假若女孩A拒绝男孩3在某一天,那么当天她留下的那个一定是更喜欢的,未来的某一天她即使拒绝了之前留下的,也说明有更更喜欢的示爱者来了,根据传递性,该性质正确。
- 性质3:每个人经过该算法的匹配后都有一个伴侣,这点不需证明。
- 性质4:TMA产生一个稳定婚烟匹配。如果一个男生和女生没能结婚,那么有两种可能:女生拒绝了男生,根据性质2,女生一定更喜欢现在的伴侣,不会产生出轨;男生没来找过女生,此时男生一定更喜欢他现在的伴侣,因此也不会产生出轨。
- 性质5(证明较复杂,参考知乎文章:稳定婚烟问题):TMA算法中男生能找到保证稳定婚烟下的最佳情侣。用算法进行的轮数来归纳证明:
首先定义:如果A和B是合适的,那么存在一种稳定婚烟匹配中A和B配对。
基础步骤:利用归谬法证明在第1轮结束时,没有男生被合适的女生拒绝,即如果一个男生被女生拒绝,那么他们一定是不合适的。设女生A在第1轮拒绝1而选择了2,那么假设在某一个稳定匹配中,A和1结婚,那么A更喜欢2,而2最喜欢A,所以会发生出轨,则这个婚烟是不稳定的,出现矛盾,假设不成立,证明完成。
归纳步骤:如果在第n轮结束时,依然没有男生被合适的女生拒绝,则证明在(n+1)轮时依然不会有。设在第(n+1)轮,女生A拒绝1而选择了2,假设A和1在某个稳定匹配中结婚,那么A更喜欢2,对2来说,在TMA算法中拒绝他的女生都是不合适的,即不可能在任何稳定匹配中出现2与她们结婚的情况,因此在假想的稳定匹配中,他的最终伴侣一定差于A,那么2也更喜欢A,所以发生出轨,出现矛盾。因此一旦女生对男生合适,那么她就不会拒绝这个男生,又因为男生是按照他的喜好顺序求爱的,因此最后找到的一定是他的稳定最佳情侣。□
- 性质6:TMA算法中女生总会找到稳定最差情侣。依然用归谬法证明,假设存在一个稳定匹配,该匹配中有一个女生G匹配到比TMA匹配中更差的情侣B’,那么她更喜欢在TMA算法中匹配到的男生B;对于B来说,由于性质5,他也一定更喜欢在TMA算法中匹配到的稳定最佳情侣G,所以出现出轨,产生矛盾,命题得证。□

我是霜_哀,在算法之路上努力前行的一位萌新,感谢你的阅读!如果觉得好的话,可以关注一下,我会在将来带来更多更全面的知识讲解!
相关文章:

MIT6.024学习笔记(二)——图论(1)
学习不是为了竞争和战胜他人,而是为了更好地了解自己和世界。 - 达赖喇嘛 文章目录 图的相关概念涂色问题基础涂色方法(贪婪算法)证明 二分图匹配问题应用:稳定婚烟问题算法性质及其证明 图的相关概念 图的定义:一组&…...

饼状图使用属性时,使用驼峰命名法
饼状图是使用D3.js等JavaScript库来绘制的,而JavaScript中的属性名通常采用驼峰式命名法,即第一个单词的首字母小写,后面单词的首字母大写,例如fontSize、fontWeight等。而CSS中的属性名采用连字符命名法,即单词之间用…...

使用Spring Boot、Spring Security和Thymeleaf的整合示例
使用Spring Boot、Spring Security和Thymeleaf的整合示例 大纲: 创建Spring Boot项目 集成Thymeleaf作为模板引擎 配置Spring Security实现身份验证和授权 创建登录页面和主页 创建管理员页面和普通用户页面 实现用户角色和权限管理 详细步骤: 创建Sprin…...
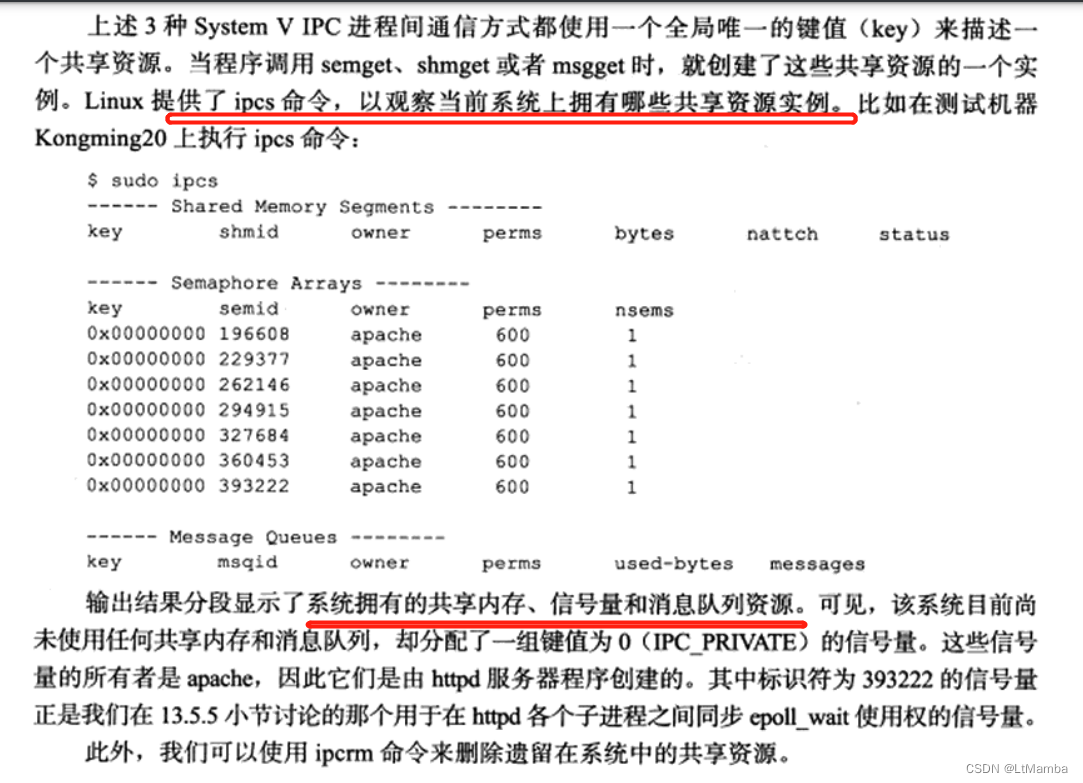
Linux--ServerProgramming--(7)IPC
1.管道 2.信号量 2.1 概念 信号量 是一个计数器,用于实现进程间互斥和同步。 信号量的取值可以是任何自然数。 最简单的信号量是只能取 0 和 1 的变量,这也是信号量最常见的一种形式,叫做二进制信号量(Binary Semaphore&#…...
最优化理论-KKT定理的推导与实现
目录 一、引言 二、最优化问题的基本概念 三、KKT条件的引入 1. 梯度条件 2. 原始可行性条件 3. 对偶可行性条件 四、KKT定理的表述 五、KKT定理的证明 1. 构造拉格朗日函数 2. 构造拉格朗日对偶函数 3. 推导KKT条件 4. 解释KKT条件 六、KKT定理的应用 七、总结 …...

chatgpt赋能python:Python中引入其他包的指南
Python中引入其他包的指南 Python是一种流行的编程语言,拥有丰富的开源软件包和库。许多Python程序将使用其他包来增强其功能。在本文中,我们将探讨如何在Python项目中使用和引入其他包。 什么是Python包和库? Python包是一组可重复使用的…...

设计模式-组合模式
应用场景 实现规则匹配的逻辑 比如> <,同时支持 and or 多个条件组合 新增一个条件就增加一个实现类 说明 对于这种需要实现规则匹配的逻辑,可以考虑使用策略模式。策略模式可以将不同的算法封装成不同的策略类,让它们可以相互替换,…...
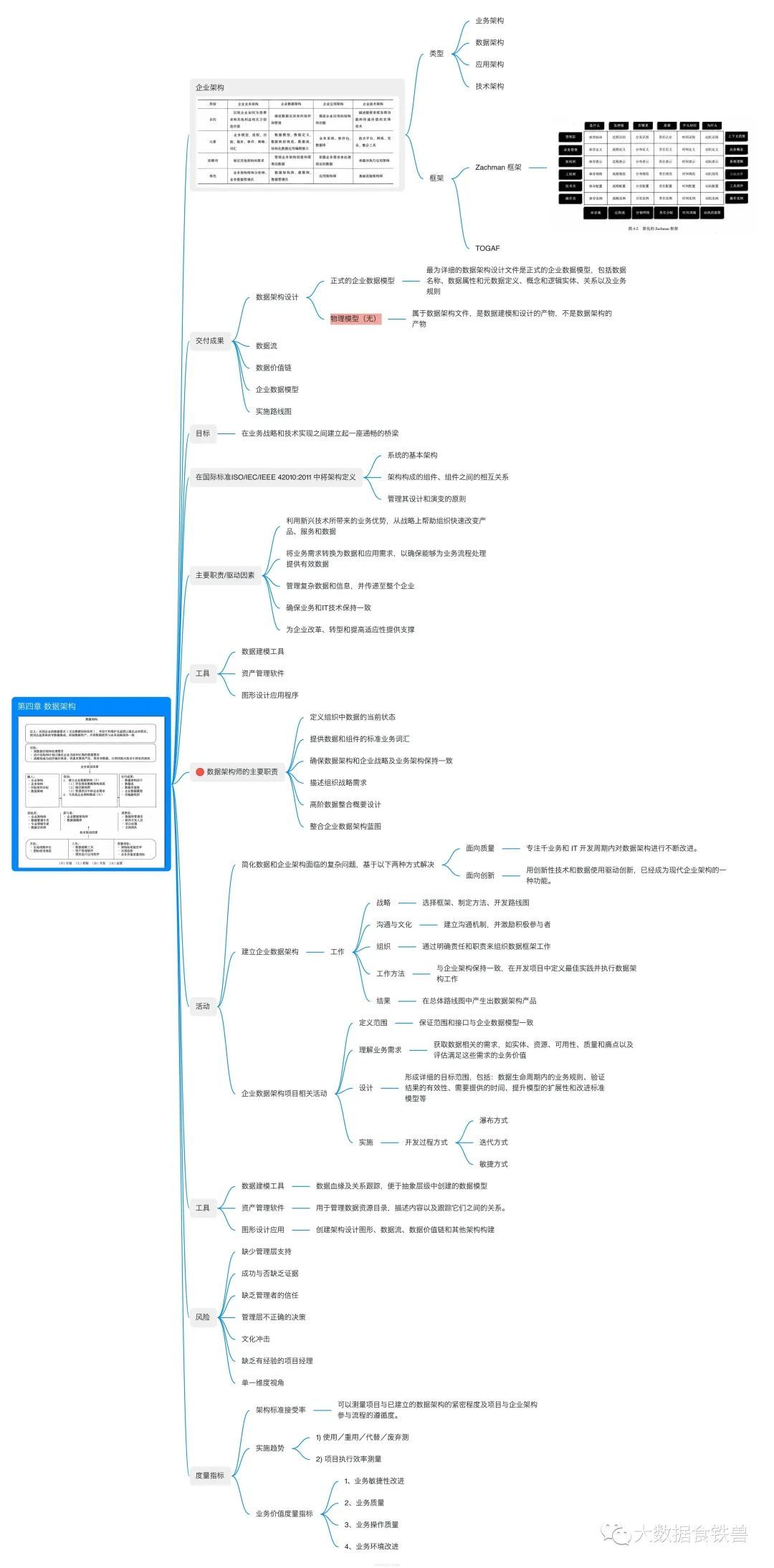
DMBOK知识梳理for CDGA/CDGP——第四章 数据架构(附常考知识点)
关 注ghz“大数据食铁兽”,回复“知识点”获取《DMBOK知识梳理for CDGA/CDGP》常考知识点(第四章 数据架构) 第四章 数据架构 第四章是CDGA|CDGP考试的重点考核章节之一,分值占比高,知识点比较密集,重点…...

MyBatisPlus总结(1.0)
MyBatis-Plus MyBatis-Plus介绍 MyBatis-Plus(简称MP)是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生 特性 无侵入:只做增强不做改变,引入它不会对现有工程产生影…...

职场老油条表示真干不过,部门新来的00后测试员已把我卷崩溃,想离职了...
在程序员职场上,什么样的人最让人反感呢? 是技术不好的人吗?并不是。技术不好的同事,我们可以帮他。 是技术太强的人吗?也不是。技术很强的同事,可遇不可求,向他学习还来不及呢。 真正让人反感的,是技术平平&#x…...

【每日挠头算法题(1)】——旋转字符串|亲密字符串
文章目录 一、旋转字符串思路1思路2 二、亲密字符串思路 总结 一、旋转字符串 点我直达终点~ 思路1 前提:如果s串和goal串长度不等,则goal串不可能是s串旋转得来,直接返回false; 通过观察,可以发现每旋转一次&#…...

什么是 tokens,ChatGPT里面的Tokens如何计数?
什么是 tokens,ChatGPT里面的Tokens如何计数? 什么是 tokens? Tokens 可以被认为是词语的片段。在 API 处理提示之前,输入会被分解成 tokens。这些 tokens 并不会精确地在单词的开始或结束处切分 - tokens 可以包含尾随的空格甚…...
工业镜头分类、相关参数含义
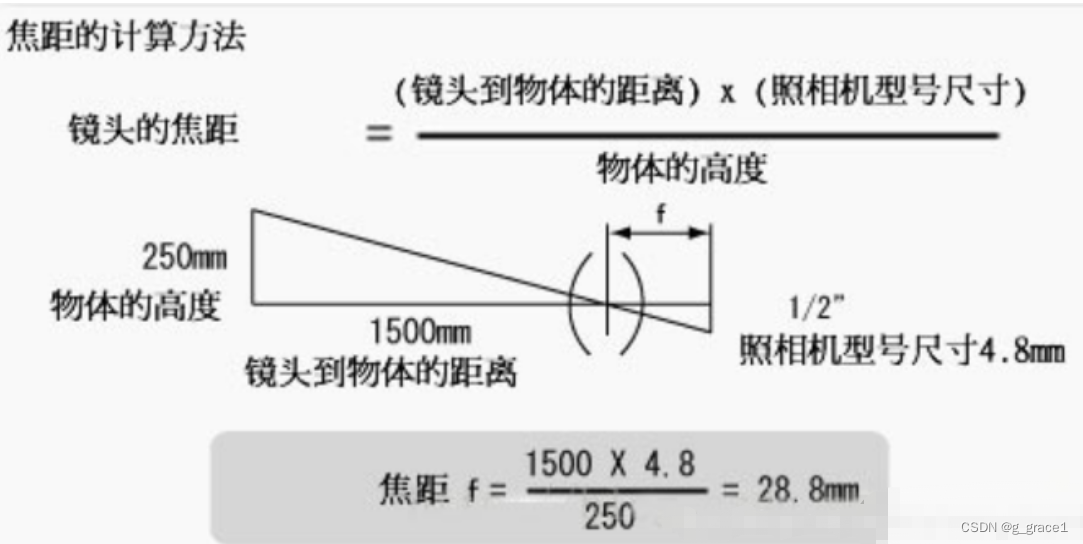
一、工业镜头参数 1、焦距/后焦距 焦距是像方主面到像方焦点的距离。后焦距指光线离开镜头最后一片镜片表面到sensor感光面的距离,如8mm,16mm,25mm等; 焦距的大小决定着视角大小,焦距数值小,视角大&#…...
)
码蹄杯语言基础:数组(C语言)
码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist ⭐MT1381逆序输出数组 定义一个长度为10的整型数组,输入10个数组元素的值,然后逆序输出他们 格式 输入格式: 输入10个数组元素的值,整型,空…...

DJ4-2 程序的装入和链接
目录 4.2.1 程序的装入 一、绝对装入方式 二 、可重定位装入方式 三、动态运行时装入方式 4.2.2 程序的链接 一、静态链接 二、装入时动态链接 三、运行时动态链接 在多道程序环境下,如果程序要运行,那么必须为之创建进程。而创建进程的第一件…...

开源项目合集....
likeshop开源商城系统,公众号商城、H5商城、微信小程序商城、抖音小程序商城、字节小程序商城、头条小程序商城、安卓App商城、苹果App商城代码全开源,免费商用。 适用场景:B2C商城、新零售商城、社交电商商城、分销系统商城、小程序商城、商…...
机器学习 | 降维问题
目录 一、主成分分析 二、奇异值分解 2.1 奇异值分解原理 2.2 奇异值分解实践 三、特征值与特征向量 一、主成分分析 主成分有如下特征: 每个主成分是原变量的线性组合;各个主成分之间互不相关;主成分按照方差贡献率从大到小依次排列&…...
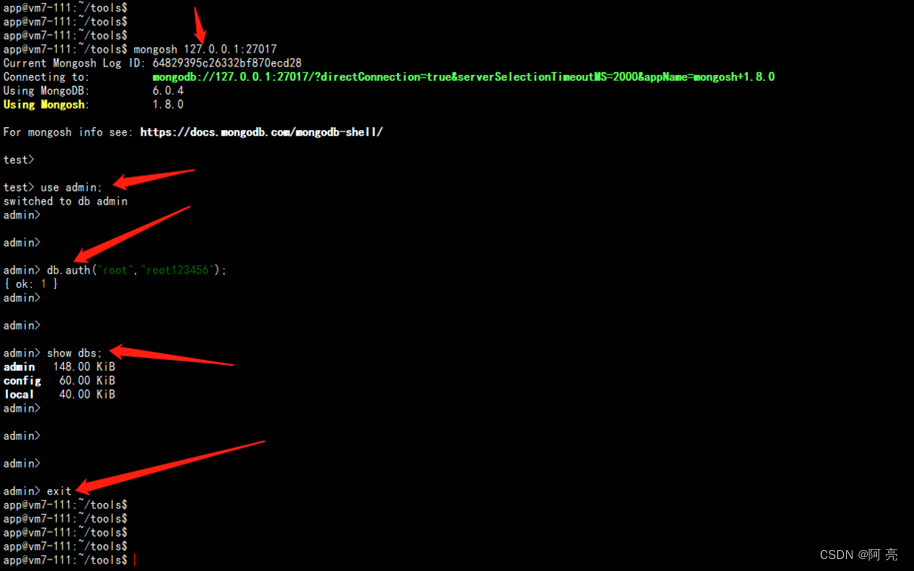
Ubuntu20.04平台下使用二进制包部署MongoDB-6.0.4单实例
文章目录 1.1 准备服务器的基本信息1.2 操作系统上创建其用户1.3 部署MongoDB服务端1.4 部署MongoDB客户端1.5 部署MongoDB 27017实例1.5.1 创建相关目录1.5.2 准备配置文件1.5.3 准备启停脚本1.5.4 进行启停测试1.5.5 加入开机自启动 1.6 创建超级管理员用户1.6.1 创建本地的超…...
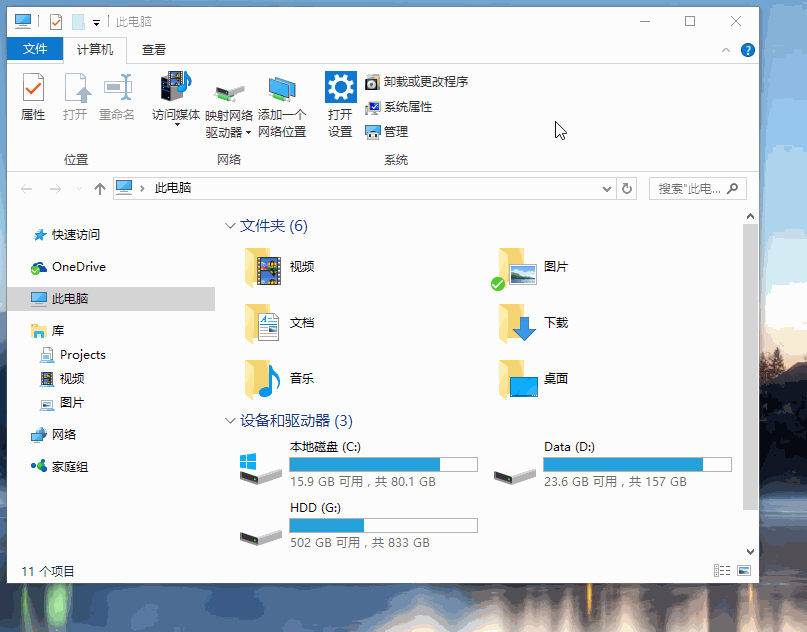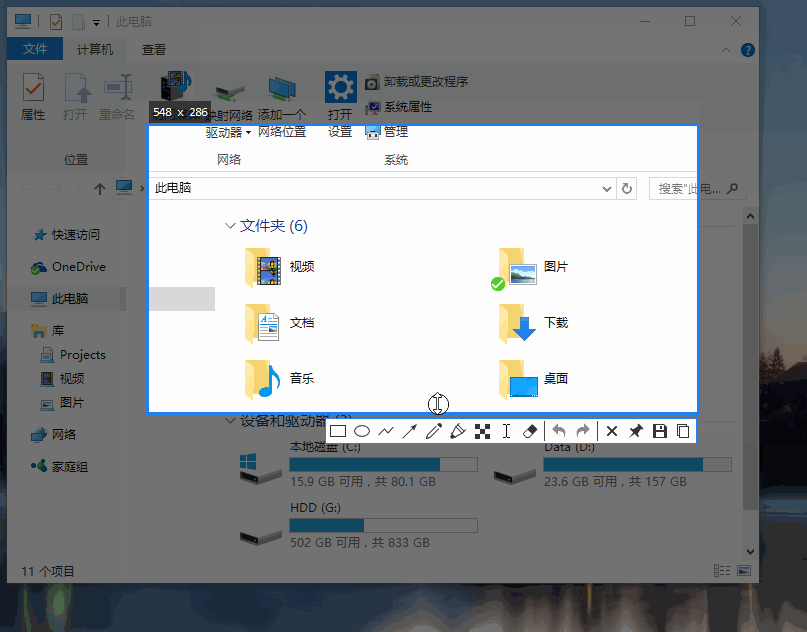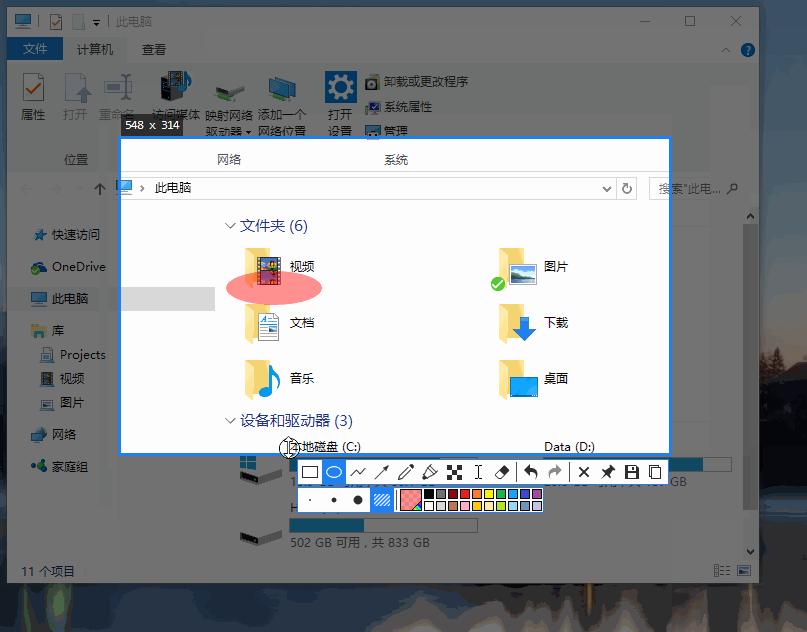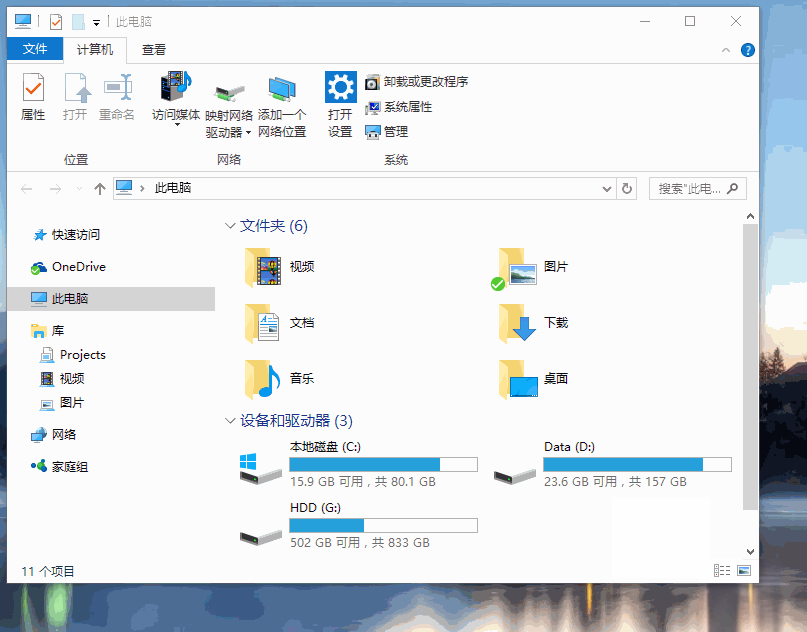
Snipaste工具推荐
Snipaste Snipaste 不只是截图,善用贴图功能将帮助你提升工作效率! 新用户? 截图默认为 F1,贴图为 F3,然后请对照着 快捷键列表 按一遍,体会它们的用法,就入门啦! 遇到了麻烦&…...
MinIO快速入门——在Linux系统上安装和启动
1、简介 MinIO 是一款基于Go语言发开的高性能、分布式的对象存储系统。客户端支持Java,Net,Python,Javacript, Golang语言。MinIO系统,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 2、环境搭建&#…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
