DC LAB8SDC约束四种时序路径分析
DC LAB
- 1.启动DC
- 2.读入设计
- 3. 查看所有违例的约束报告
- 3.1 report_constraint -all_violators (alias rc)
- 3.2 view report_constraint -all_violators -verbose -significant_digits 4 (打印详细报告)
- 4.查看时序报告 report_timing -significant_digits 4
- 5. 约束组合逻辑(adr_i/coff到comb logic到dout)
- 5.1 创建虚拟时钟
- 5.1.1 set_input_delay 用法
- 5.2 创建虚拟时钟vclk后再report_timing
- 5.2.1 组合逻辑约束,clk与vclk logically_exclusive(设置`clk-->comb-->vclk`, `vclk-->comb-->clk`为false)
- 5.2.2 设置`clk与vclk llogically_exclusive`后再去report_timing -group vclk -significant_digits 4
- 5.3 查看clk的timing, report_timing -group clk -significant_digits 4
- 5.3.1 组合逻辑约束,`设置clk--->comb-->clk为false path`
- 5.3.2 设置`clk--->comb-->clk为false path` 后再report_timing -from $in_ports -to [all_outputs]
- 6. 查看clk group timing ,report_timing -group clk
- 6.1 设置`mul_result_reg*/D `(reg2reg)多周期检查setup `set_multicycle_path `
- 6.1.1 设置完setup,多周期再检查reg2reg(`coeff_q_reg_14_ ` to `mul_result_reg_31_`)的setup
- 6.2 检查hold(肯定violation,多周期设置没设置hold,只设置了setup,hold现在在5ns检查太严格了)
- 6.2.1 设置 `mul_result_reg*/D ` (reg2reg)多周期检查hold
- 6.2.2 设置hold多周期后再检查
- 7.report_constraint -all_violators
- 8.四种时序路径总结
- 8.1 in2reg
- 8.2 reg2reg
- 8.3 reg2out
- 8.4 in2out
- 8.4.1 in2out`(adr_i[0]-->dout[6]) `demo
- 8.4.2 in2out`(coeff[5]-->dout[6]) `demo
- 9.打印所有port、cells、pins
- get_ports
- get_cells
- get_pins
1.启动DC
dc_shell-t -64bit -topo
2.读入设计
read_ddc EXCEPTIONS.ddc
current_design EXCEPTIONS
link
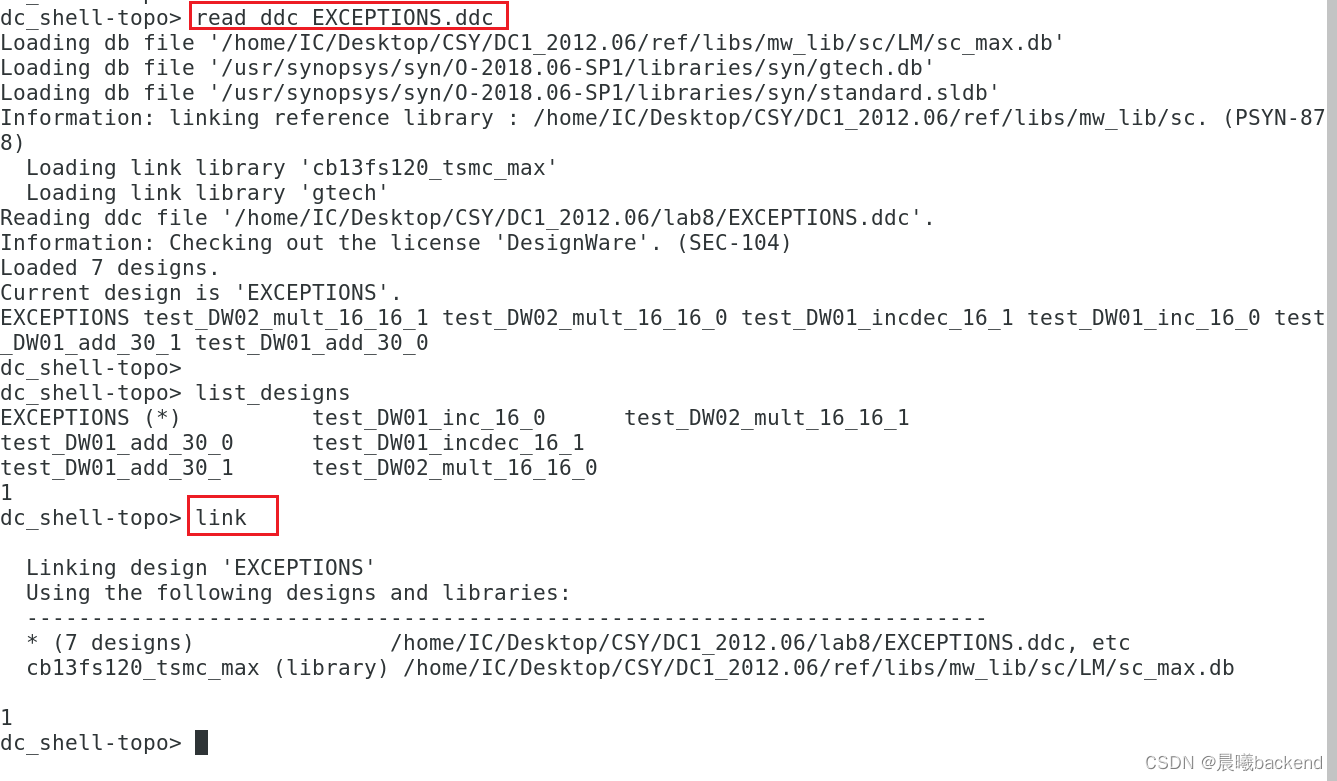
3. 查看所有违例的约束报告
3.1 report_constraint -all_violators (alias rc)
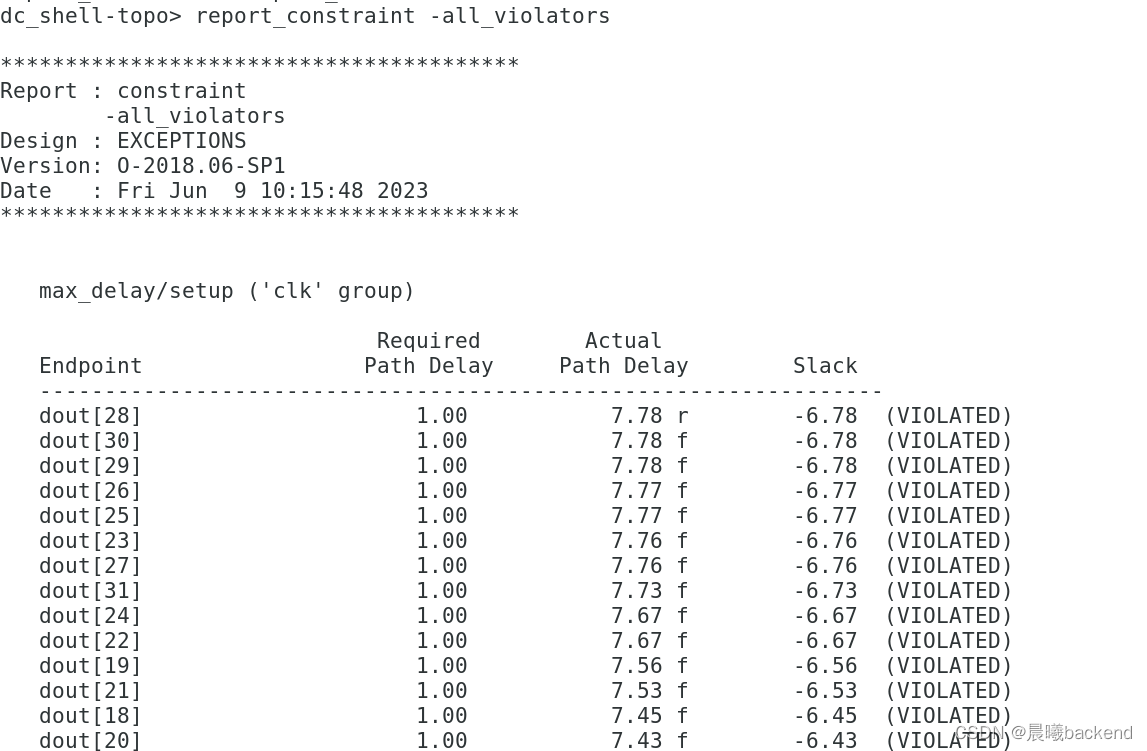
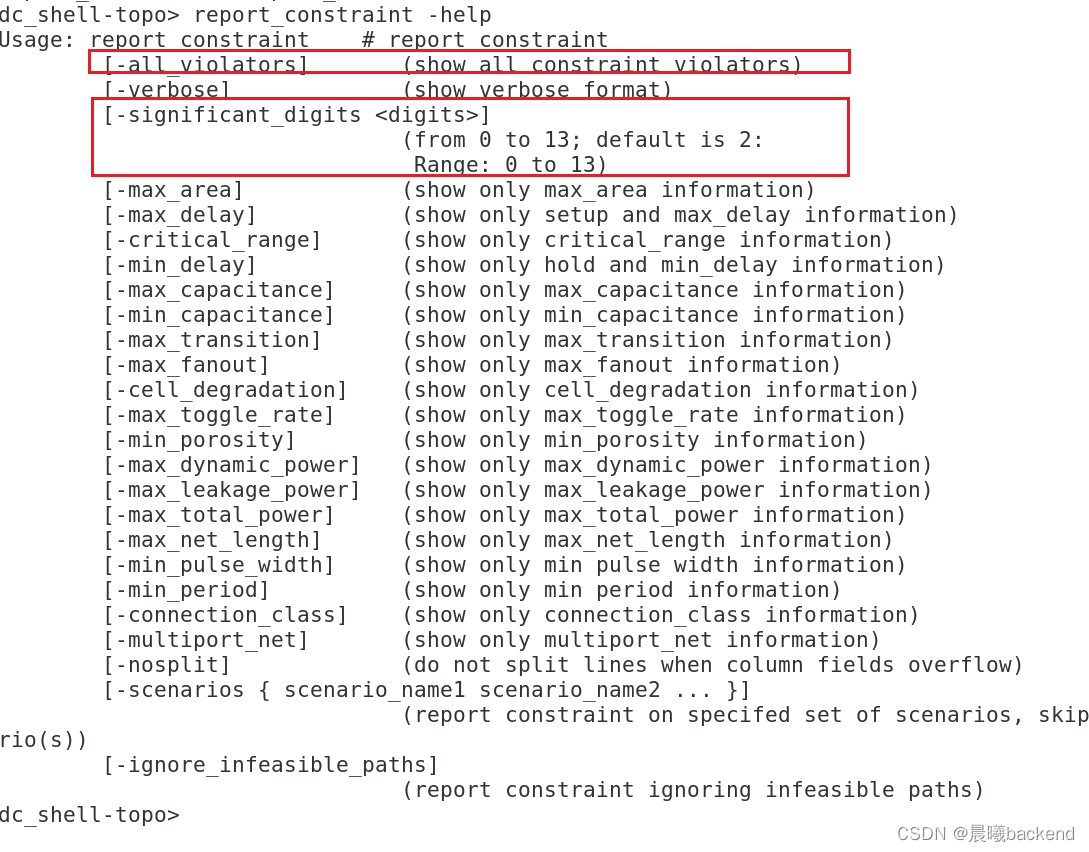
3.2 view report_constraint -all_violators -verbose -significant_digits 4 (打印详细报告)
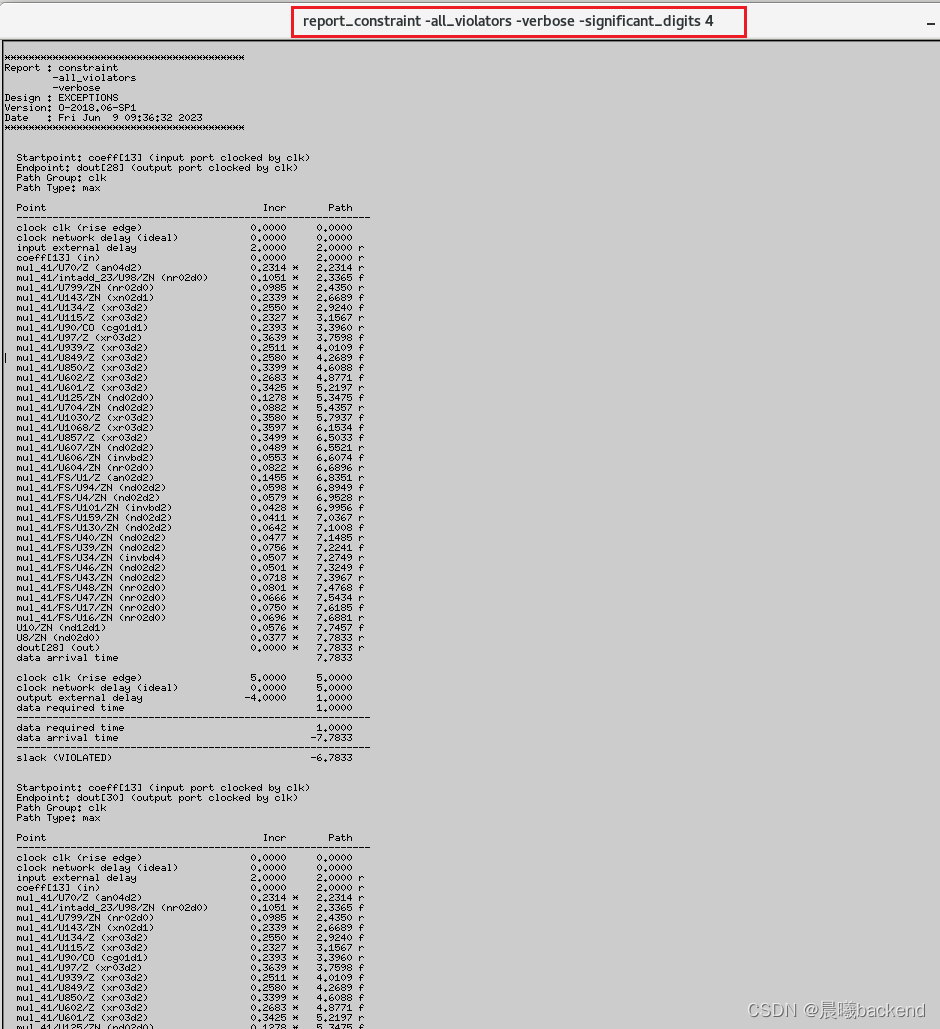
4.查看时序报告 report_timing -significant_digits 4
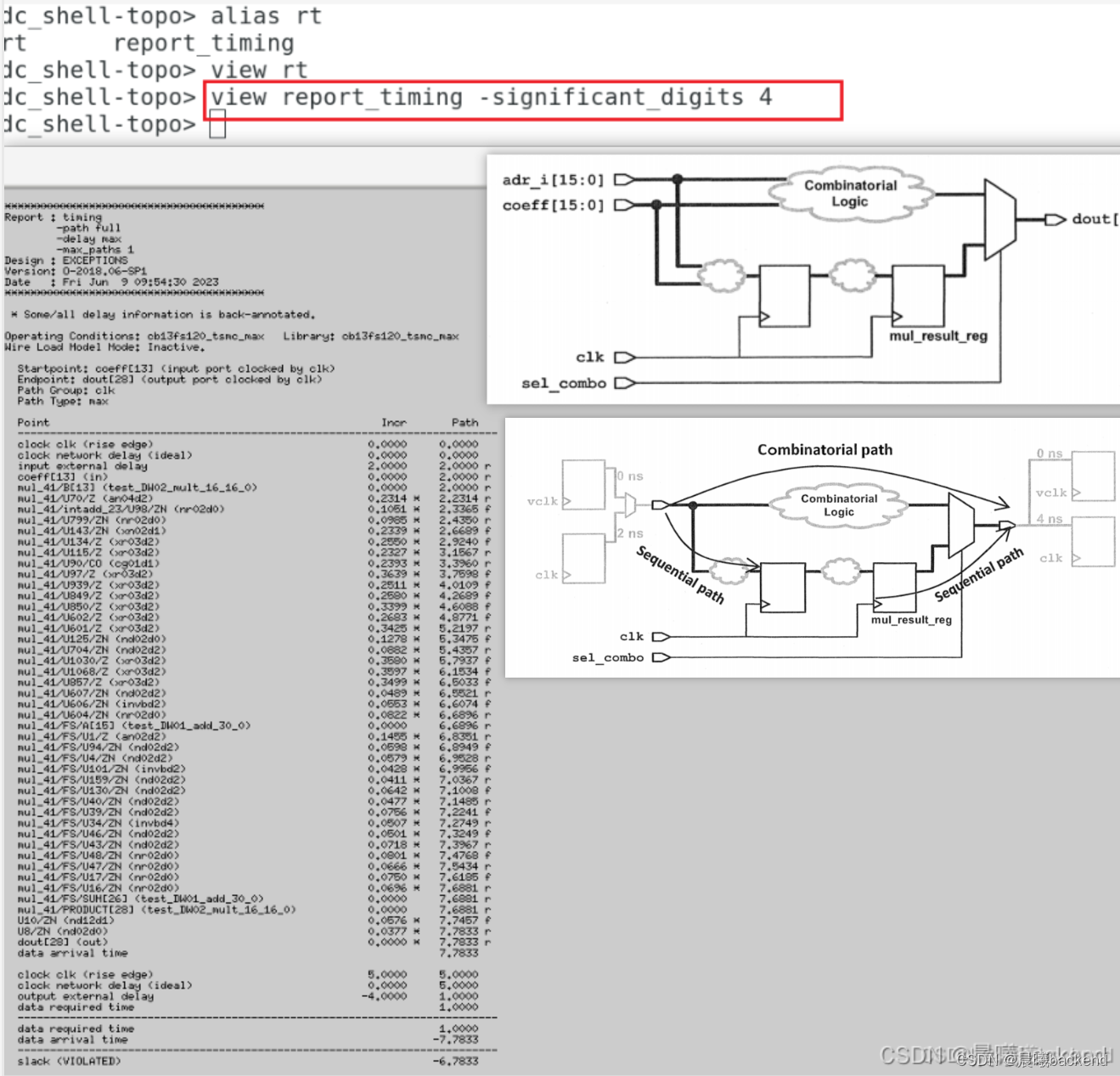
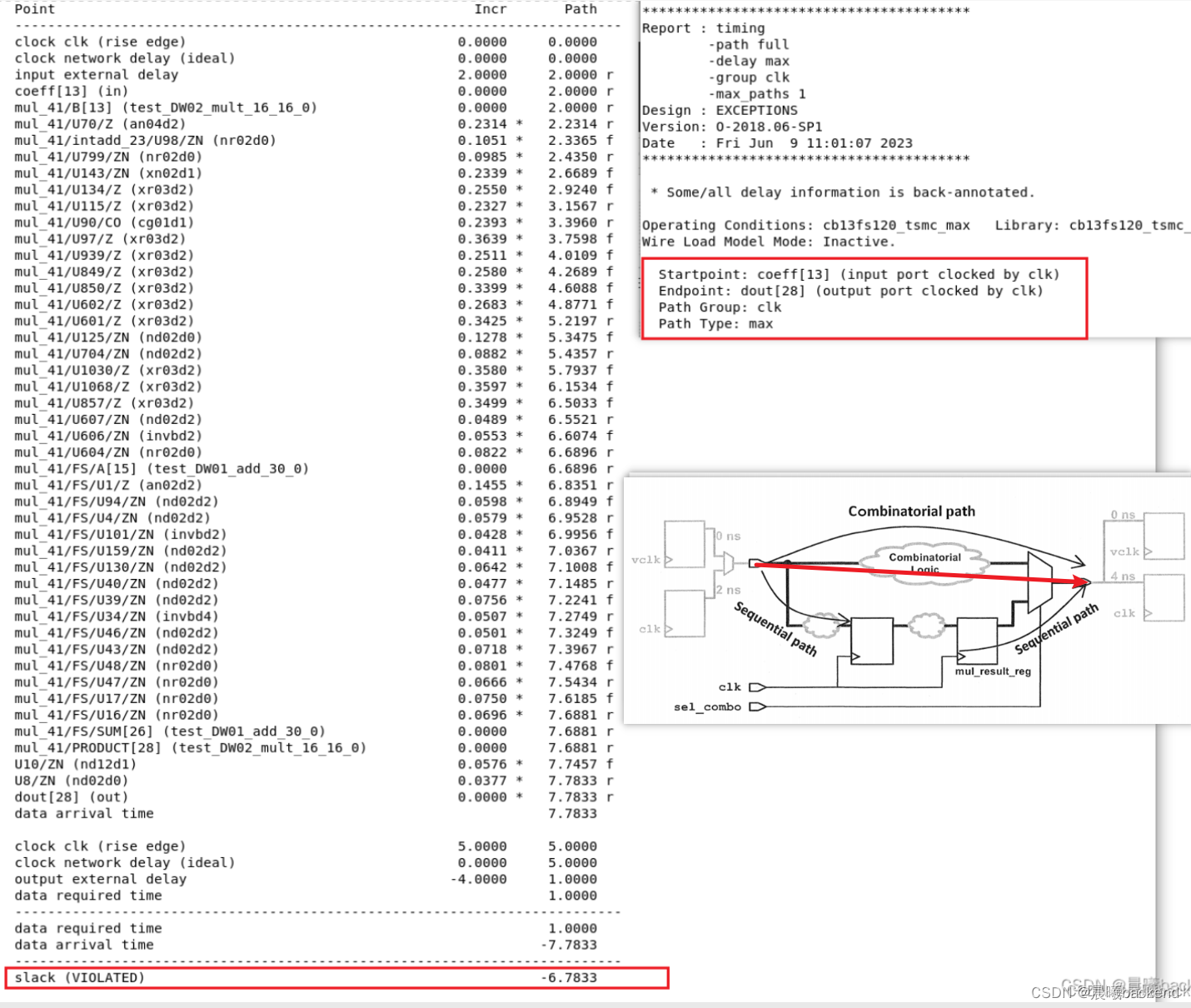
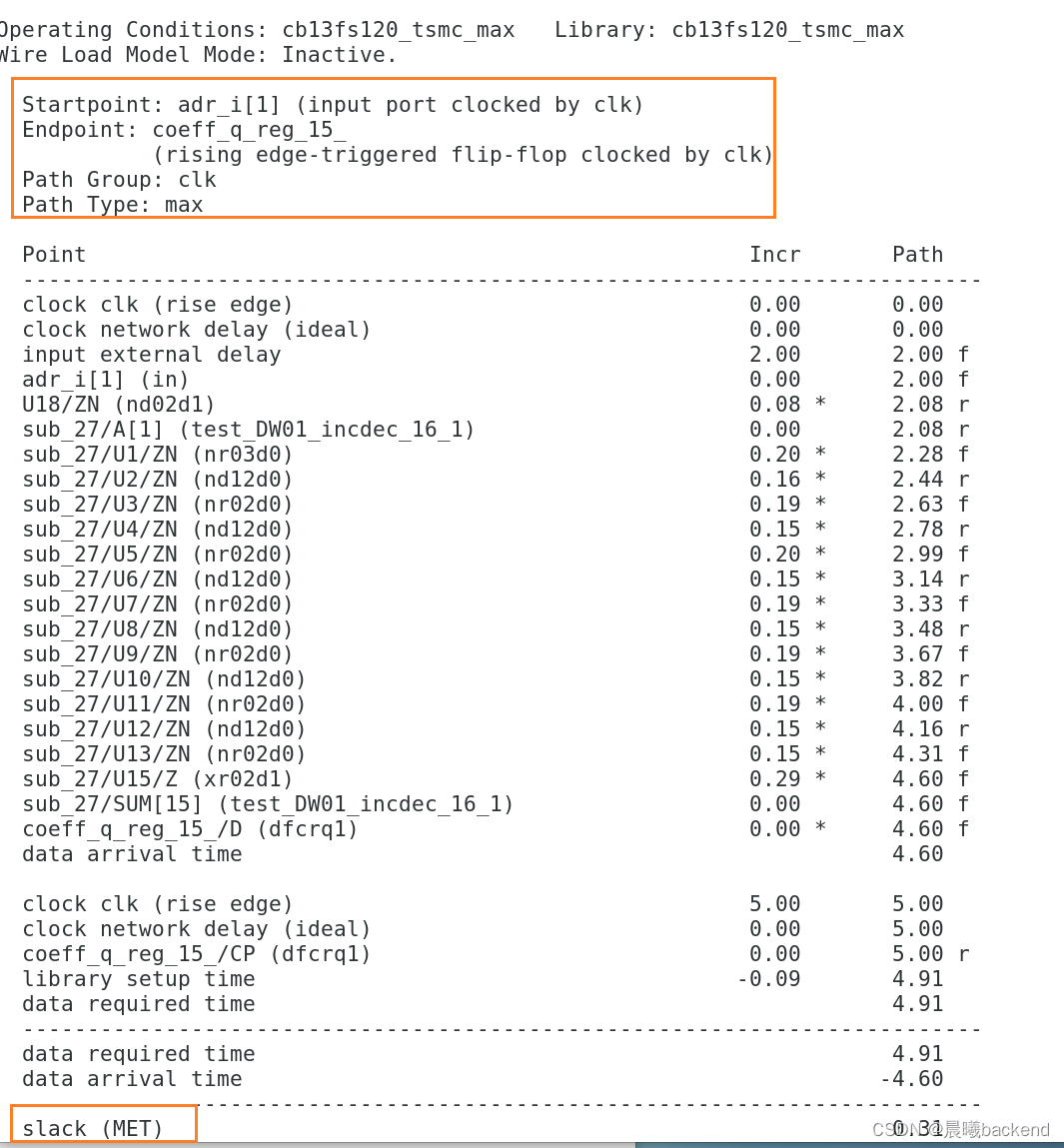
- 组合逻辑延时是7.7833-2=5.7833
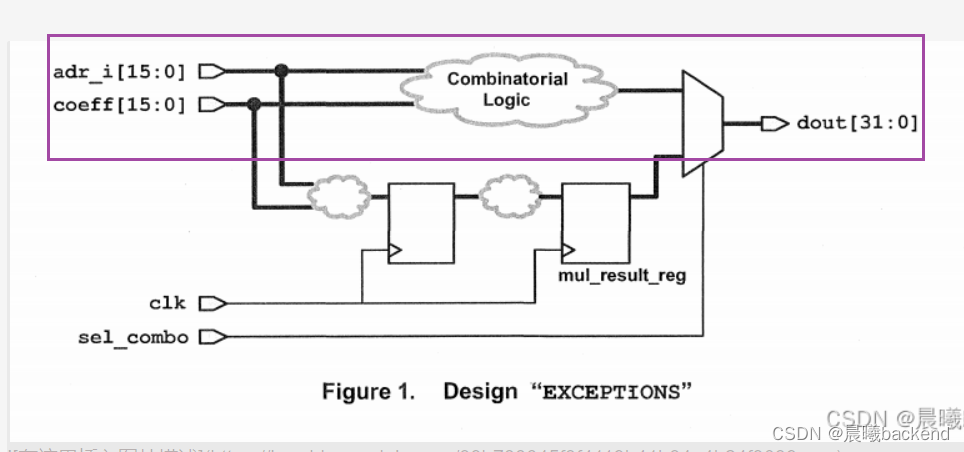
- 对于adr_i/coff到comb logic到dout,
(in2out,应该定义虚拟时钟vclk),将clk-->comb-->clk,clk-->comb-->vclk,vclk-->comb-->clk,这三条设置false - 上图是adr_i/coff到comb logic到dout时序路径,有vio(clk–>input delay 2ns -->coff --> comb logic 5.7833ns --> dout) 这条路径应设置false path
5. 约束组合逻辑(adr_i/coff到comb logic到dout)
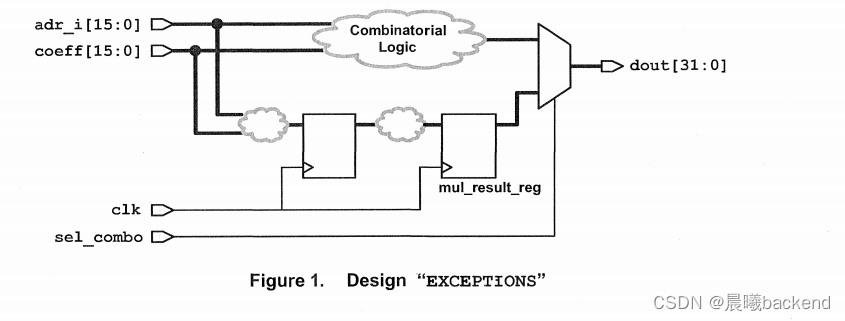
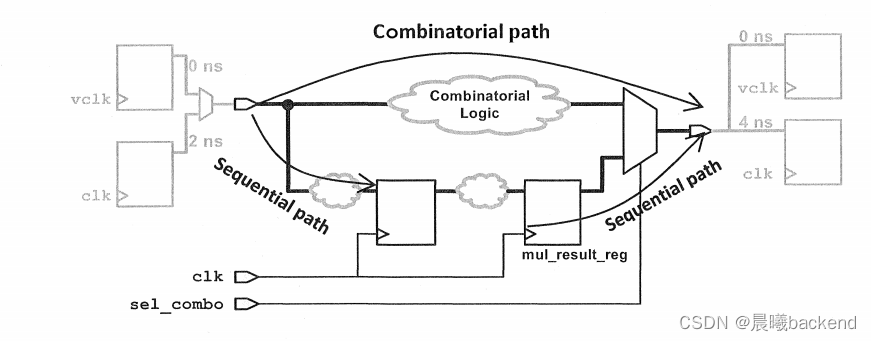
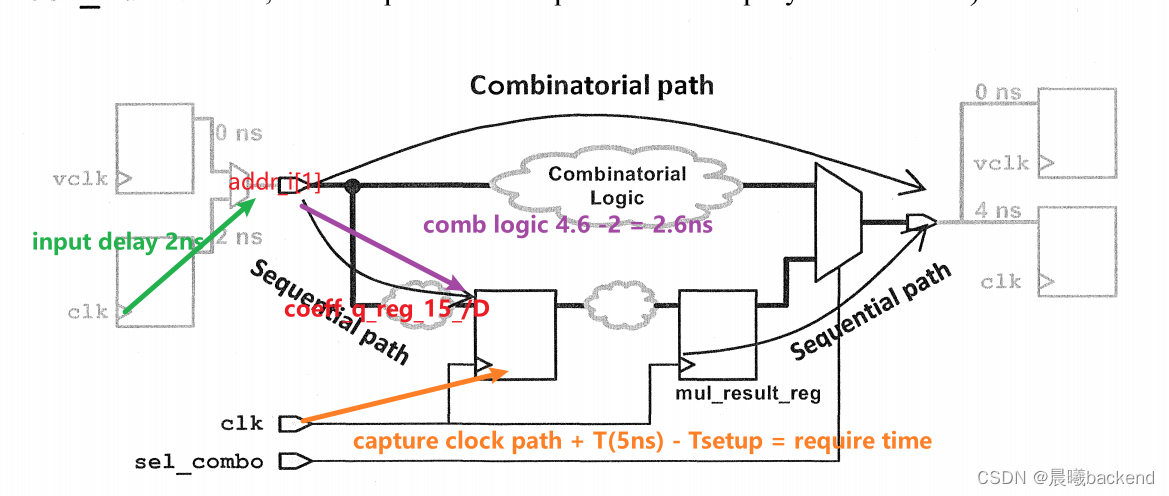
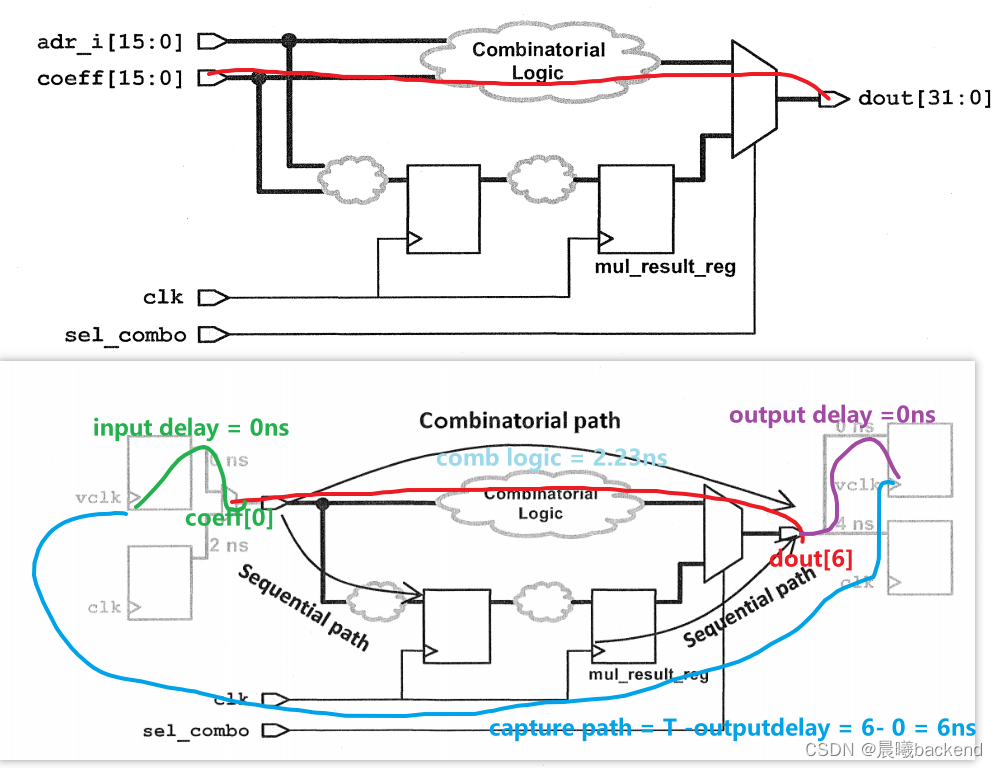
- To accomplish this,the combinatorial paths will be constrained using a new virtual clock which you will call vclk.
- The sequential paths are already constrained using the 5ns design clock clk,and input and output delays of 2ns and 4ns,respectively.
- The following schematic illustrates this concept (note that the two input ports, adr_ i and coeff,are collapsed into one port here to simplify the schematic):
5.1 创建虚拟时钟
create_clock -name vclk -period 6
set in_ports [get_ports "coeff* adr_i*"]
set_input_delay 0 -clock vclk -add_delay $in_ports
set_output_delay 0 -clock vclk -add_delay [all_outputs]
5.1.1 set_input_delay 用法
dc_shell-topo> set_input_delay -help
Usage: set_input_delay # set input_delay[-clock clock_name] (relative clock)[-clock_fall] (delay is relative to falling edge of clock)[-level_sensitive] (delay is from level-sensitive latch)[-rise] (specifies rising delay)[-fall] (specifies falling delay)[-max] (specifies maximum delay)[-min] (specifies minimum delay)[-add_delay] (don't remove existing input delay)[-network_latency_included](specifies that clock_network_latency is included)[-source_latency_included](specifies that clock_source_latency is included)[-reference_pin pin_list](list of pins)delay_value (path delay)port_pin_list (list of ports and/or pins)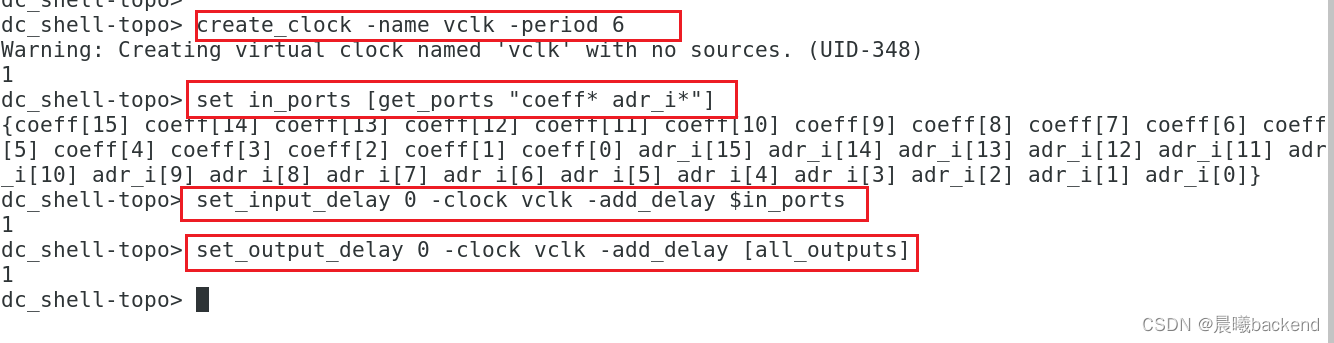
5.2 创建虚拟时钟vclk后再report_timing
view report_timing -group vclk -significant_digits 4
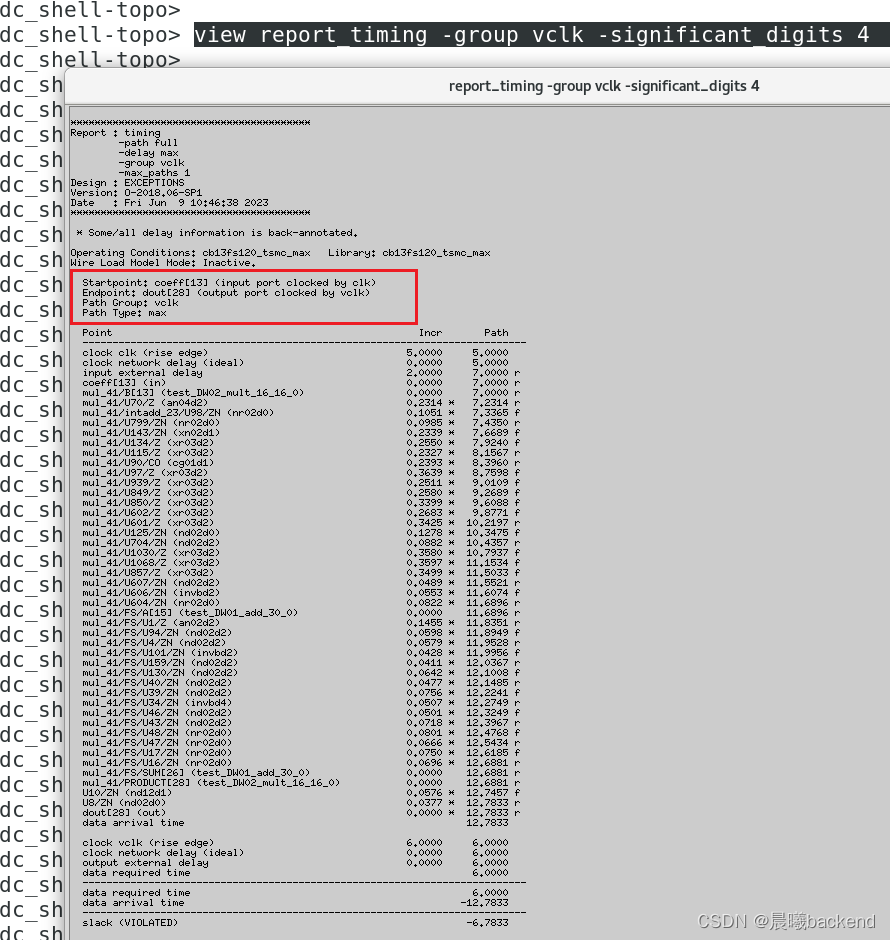
- 组合逻辑的路径应该只有vclk约束,设置
clk-->comb-->clk,clk-->comb-->vclk,vclk-->comb-->clk为false - The launch clock is vclk and the capture clock is vclk . This is not correct!
- The combinatorial paths should be constrained only by vclk . The two clocks should not interact.
5.2.1 组合逻辑约束,clk与vclk logically_exclusive(设置clk-->comb-->vclk, vclk-->comb-->clk为false)
- 对于
clk-->comb-->clk只有手动设置false了 (5.3.1)
#两种时钟,四种组合,约束后只能从clk到clk或者vclk到vclk
#
set_clock_group -name false_grp1 -logically_exclusive -group clk -group vclk# Altenatively:
#
# set_false_path -from [get_clocks clk] -to [get_clocks vclk]
# set_false_path -from [get_clocks vclk] -to [get_clocks clk]
5.2.2 设置clk与vclk llogically_exclusive后再去report_timing -group vclk -significant_digits 4
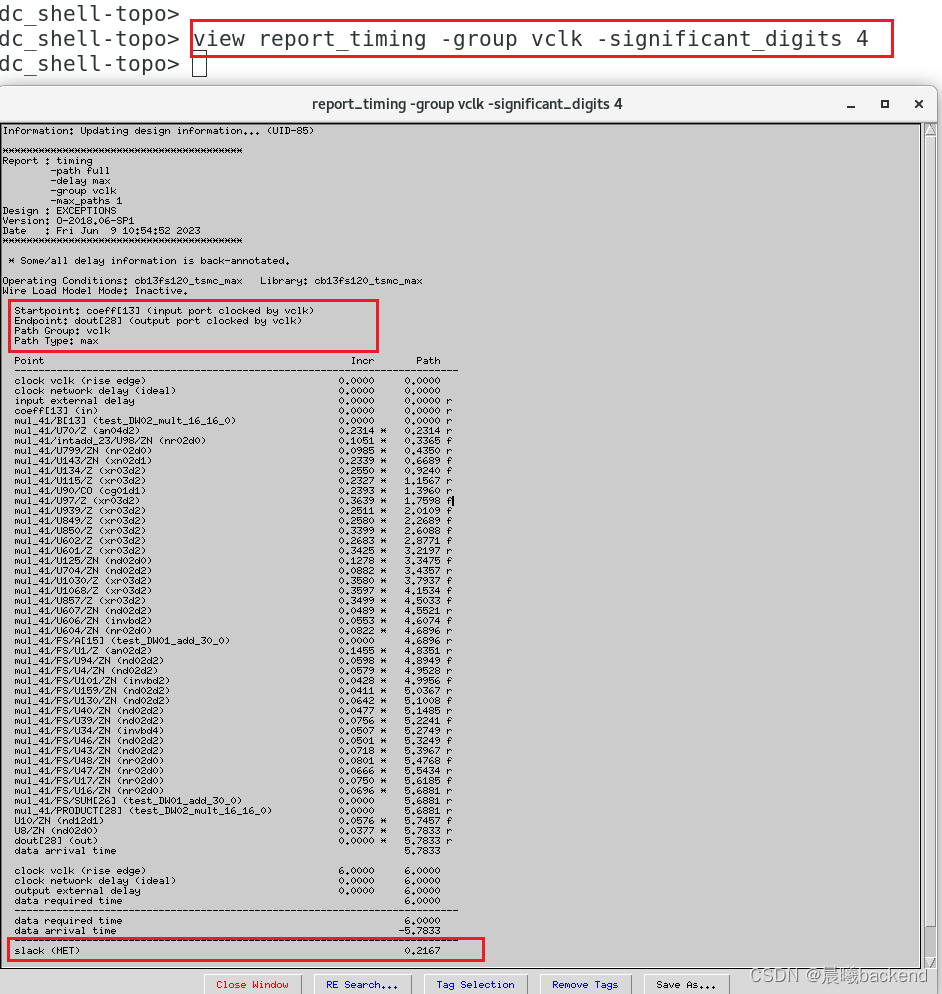
- 组合逻辑延时 5.7833ns
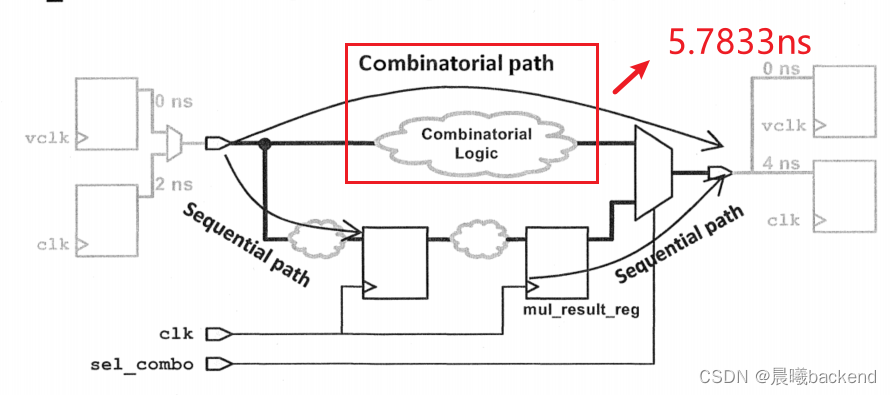
5.3 查看clk的timing, report_timing -group clk -significant_digits 4
- 这里不会显示
vclk-->clk,因为前面(5.2.1)设置了logically exclusive - 只会显示
clk-->clk
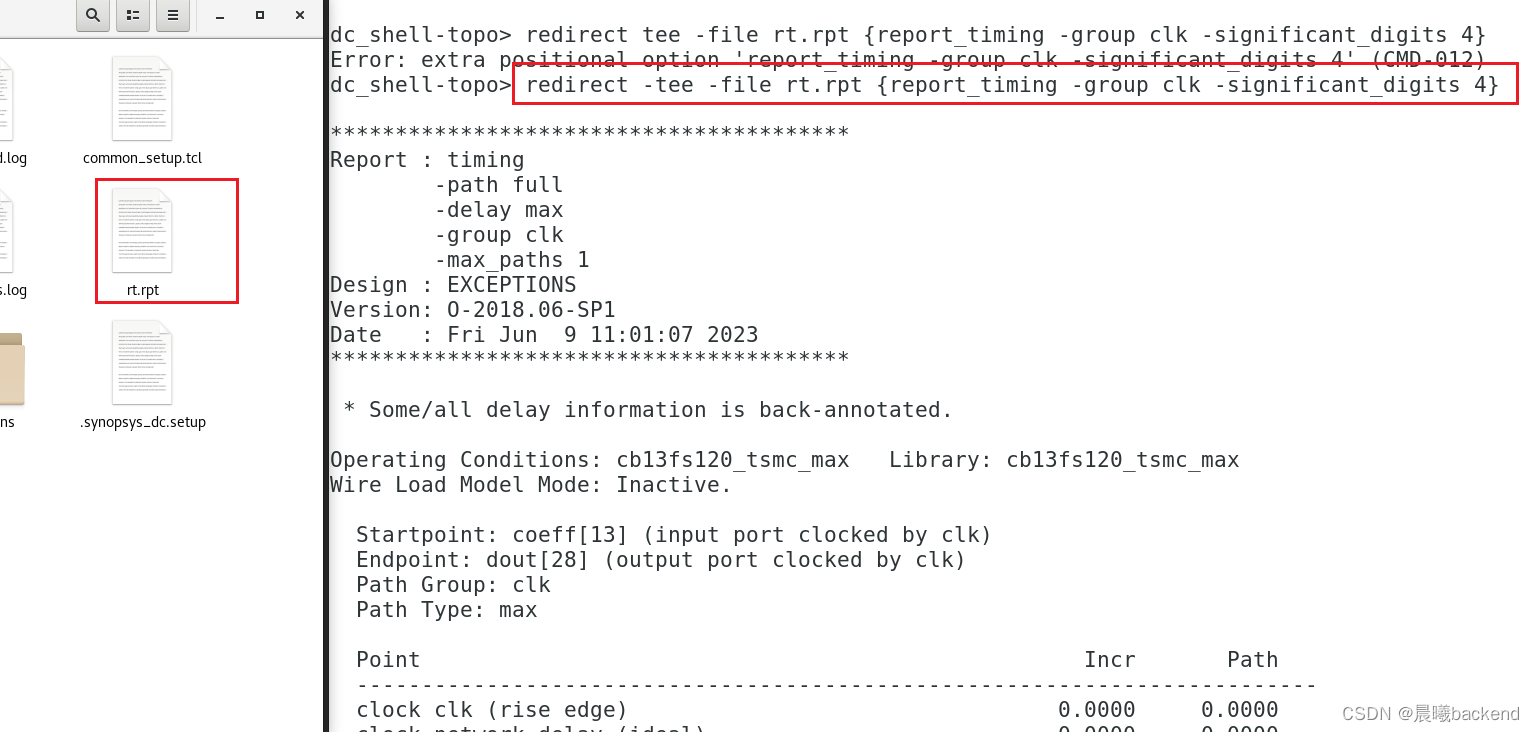
- 上图是addi/coff到comb到dout的时序路径,有vio(clk–>input delay 2ns -->coff --> comb logic 5.7833ns --> dout) 这条路径设置false path ,
- 这条路径用虚拟时钟vclk检查
- 前面5.2.1虽然设置了logic exclusive(
clk-->comb-->vclk,vclk-->comb-->clk为false),但是clk—>comb–>clk还是得手动去 false
5.3.1 组合逻辑约束,设置clk--->comb-->clk为false path

set_false_path -from [get_clocks clk] \-through $in_ports \-through [all_outputs] -to [get_clocks clk]

5.3.2 设置clk--->comb-->clk为false path 后再report_timing -from $in_ports -to [all_outputs]
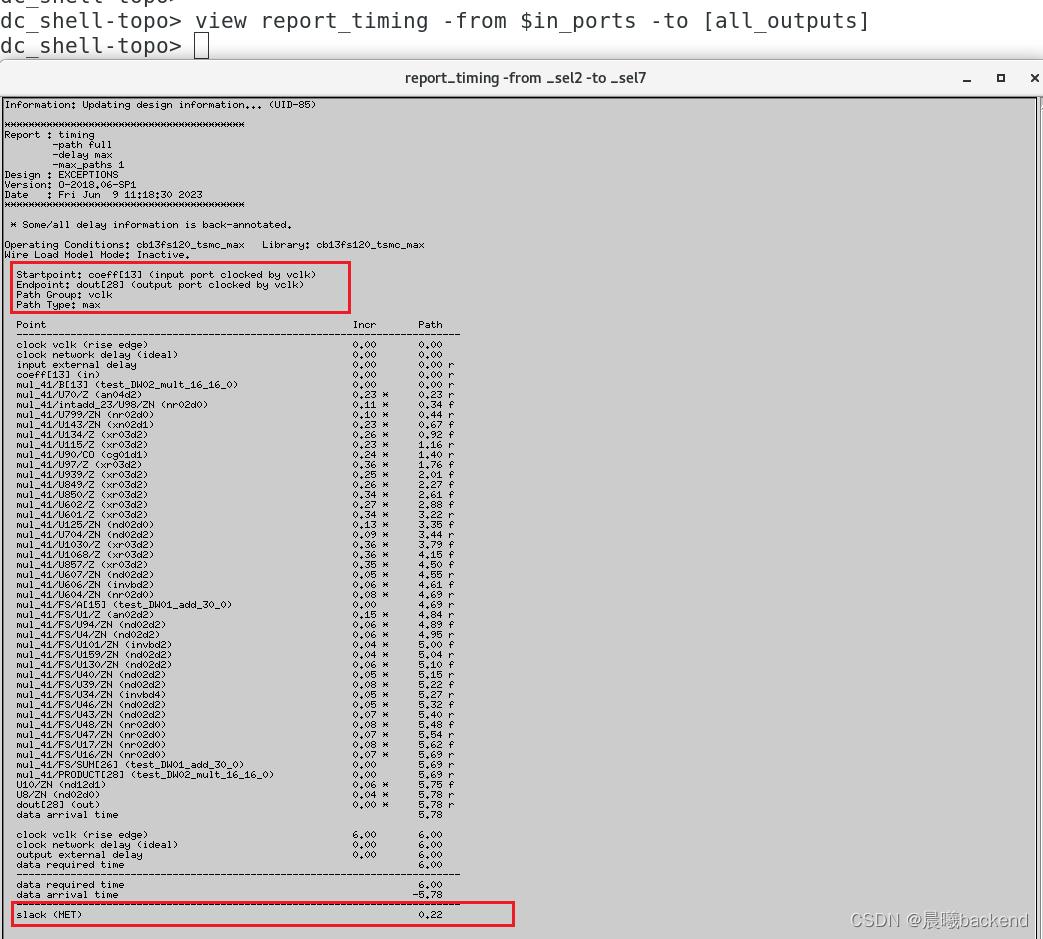
- 由于设置
clk-->comb-->clk,clk-->comb-->vclk,vclk-->comb-->clk为false,故只会显示vclk–>vcomb–>clk这条时序路径
6. 查看clk group timing ,report_timing -group clk
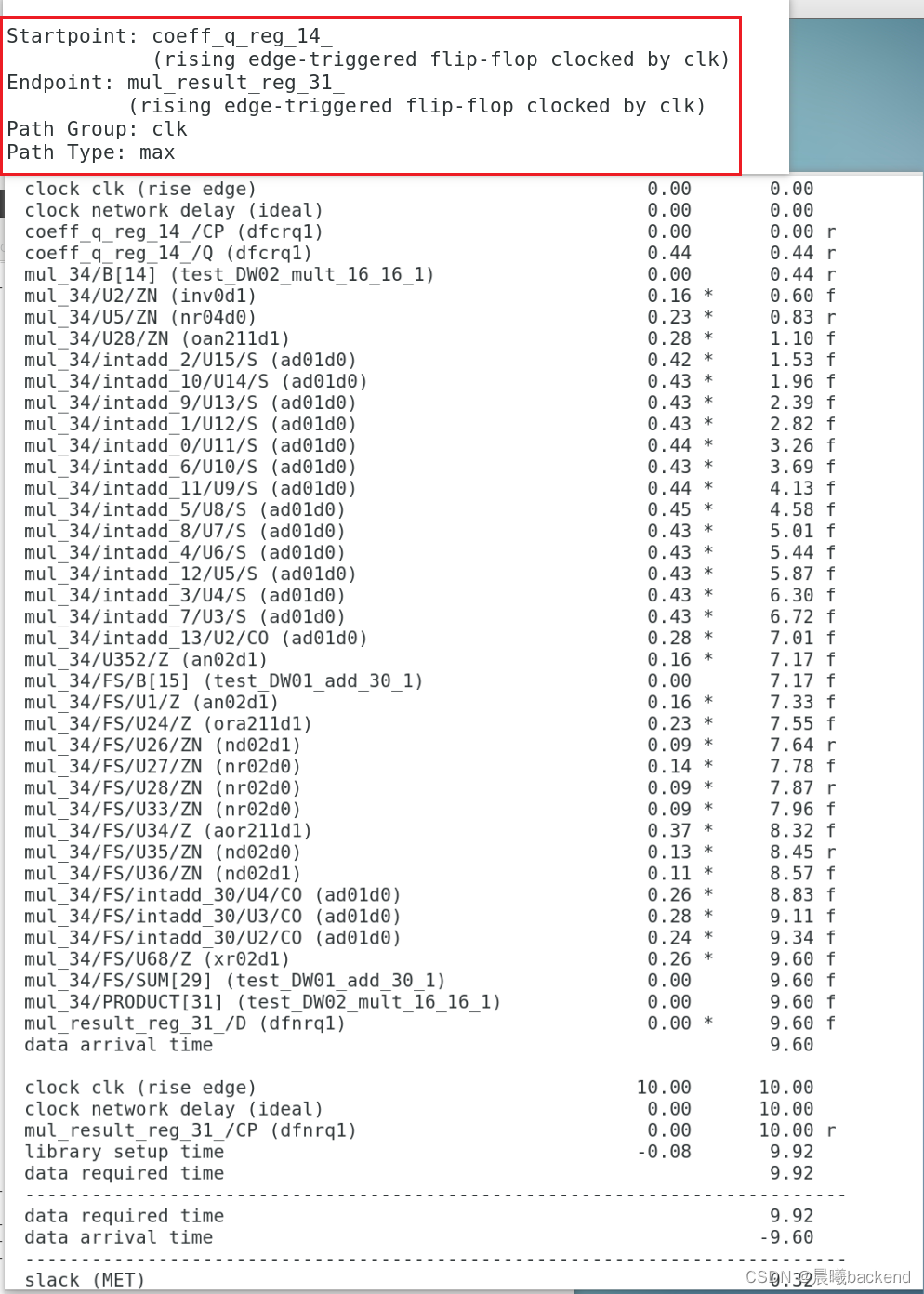
- 从下图可以看出reg2reg 中间组合逻辑延时为9.1589ns,Tcq=0.4383
- 组合逻辑介于一个周期和两个周期之间,所以设置multicycle path(setup设置N,hold则对应N-1)
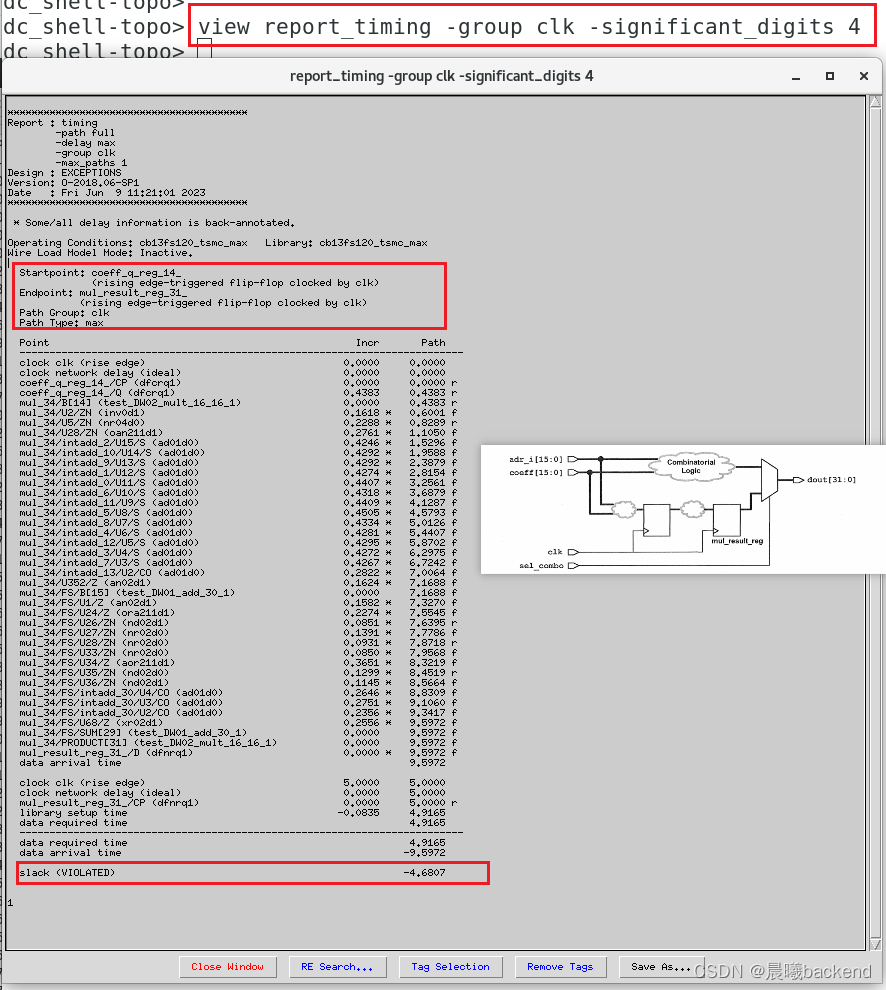
两个寄存器间的Tcq+Tcomb = 9.5943,单周期检查太严格,故设置多周期检查,setup在第二个周期在检查
6.1 设置mul_result_reg*/D (reg2reg)多周期检查setup set_multicycle_path
##若setup设置N,hold 对应设置为N-1
set_multicycle_path 2 -setup -to mul_result_reg*/D
6.1.1 设置完setup,多周期再检查reg2reg(coeff_q_reg_14_ to mul_result_reg_31_)的setup
- 由于只设置了setup,所以这里检查setup的 comb max delay是没有问题的
- 但是检查hold,就过于严苛了
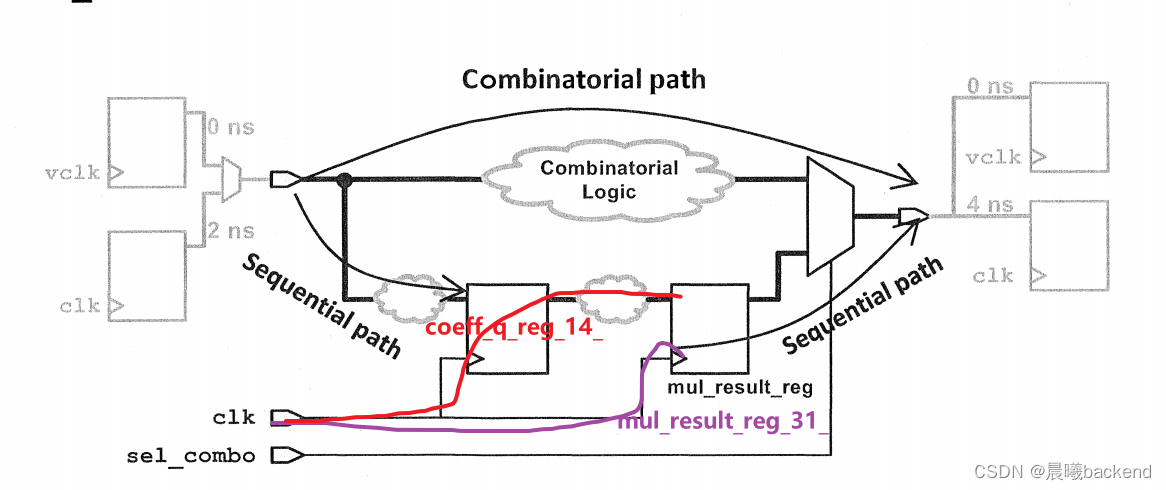
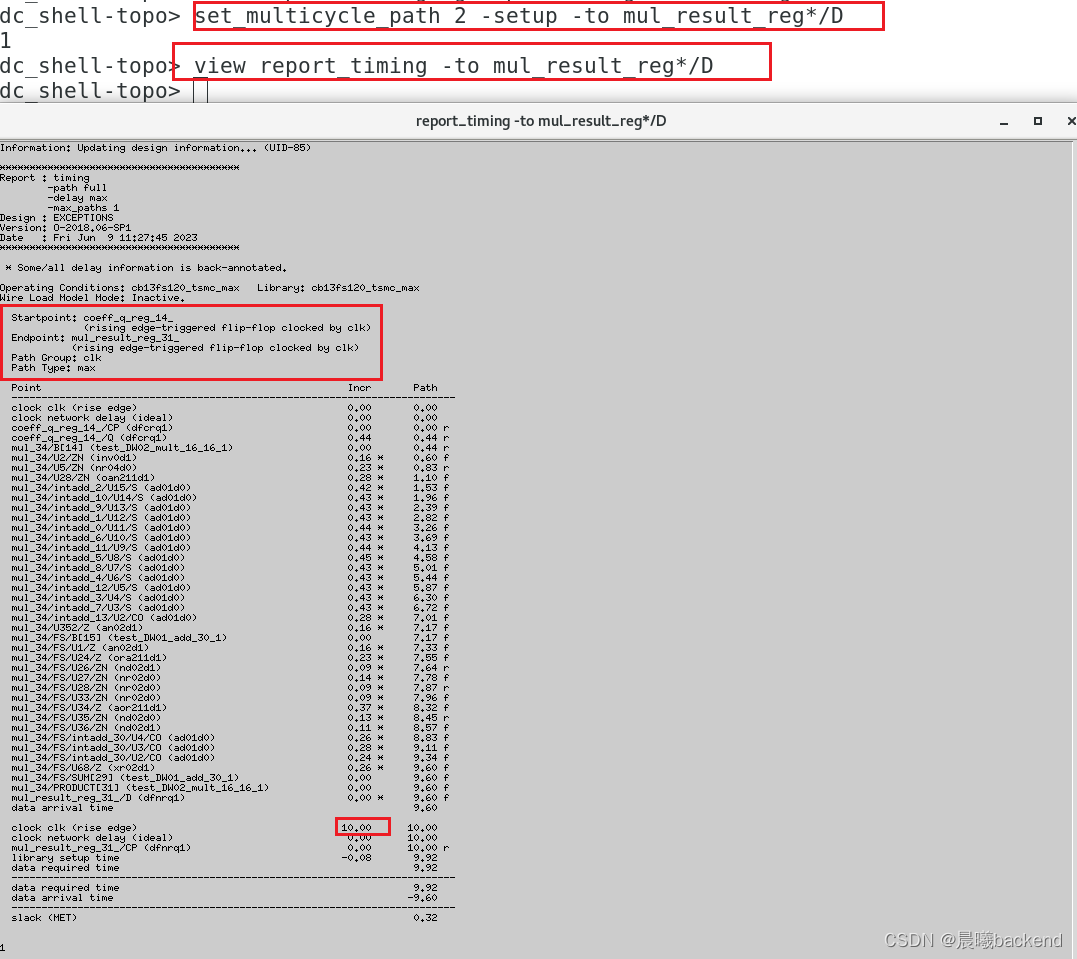
6.2 检查hold(肯定violation,多周期设置没设置hold,只设置了setup,hold现在在5ns检查太严格了)
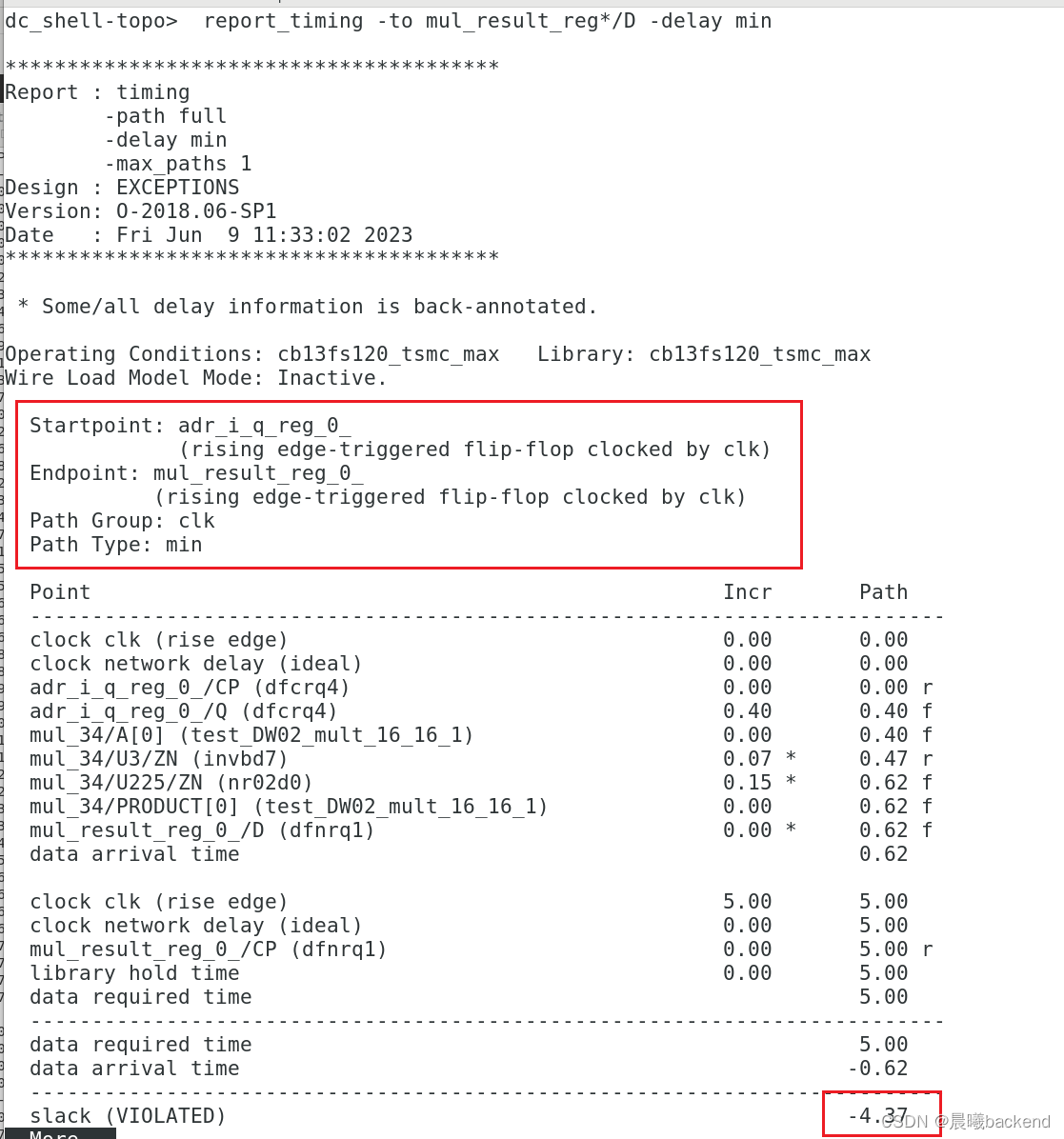
6.2.1 设置 mul_result_reg*/D (reg2reg)多周期检查hold
set_multicycle_path 1 -hold -t o mul_result_reg*/D
6.2.2 设置hold多周期后再检查
report_timing -significant_digits 4 -to mul_result_reg*/D -delay min
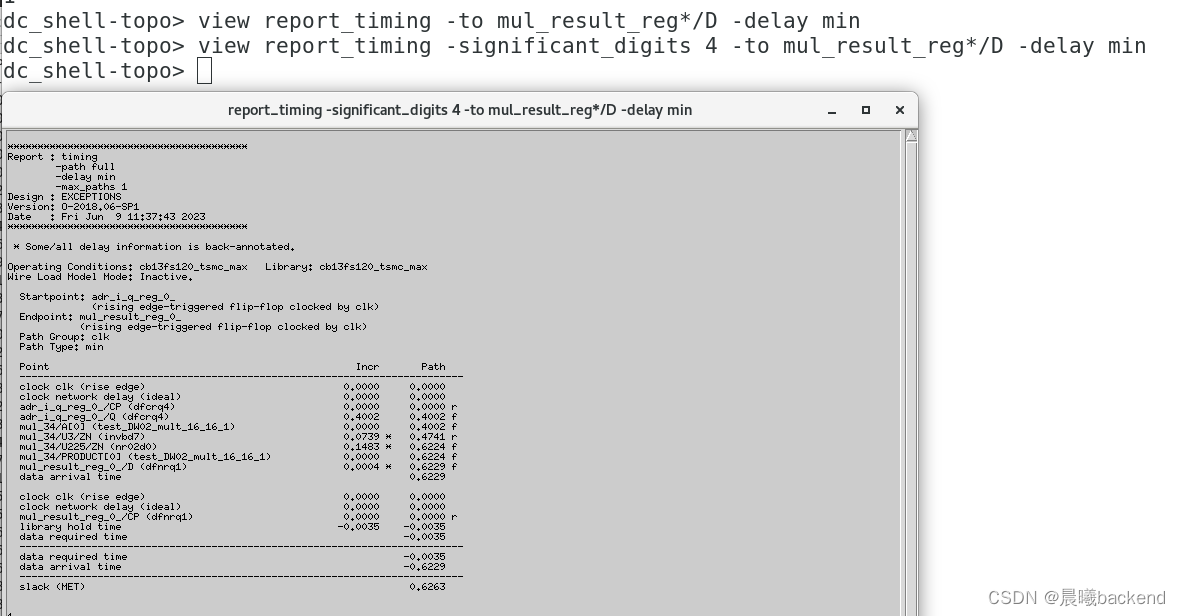
7.report_constraint -all_violators
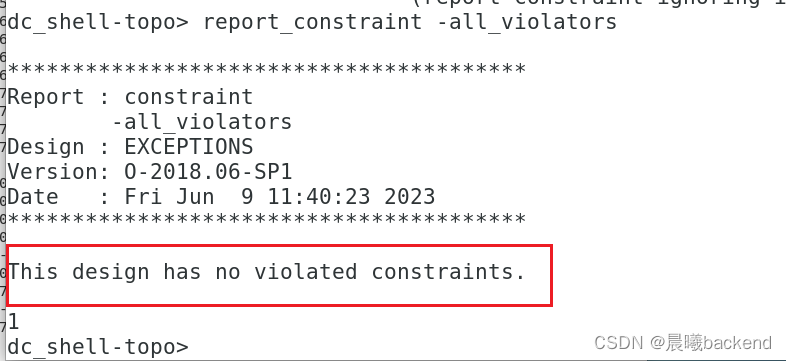
- 所有timing vio都已经清除完毕了
8.四种时序路径总结
8.1 in2reg
report_timing -group clk

[-add_delay] (don't remove existing input delay)
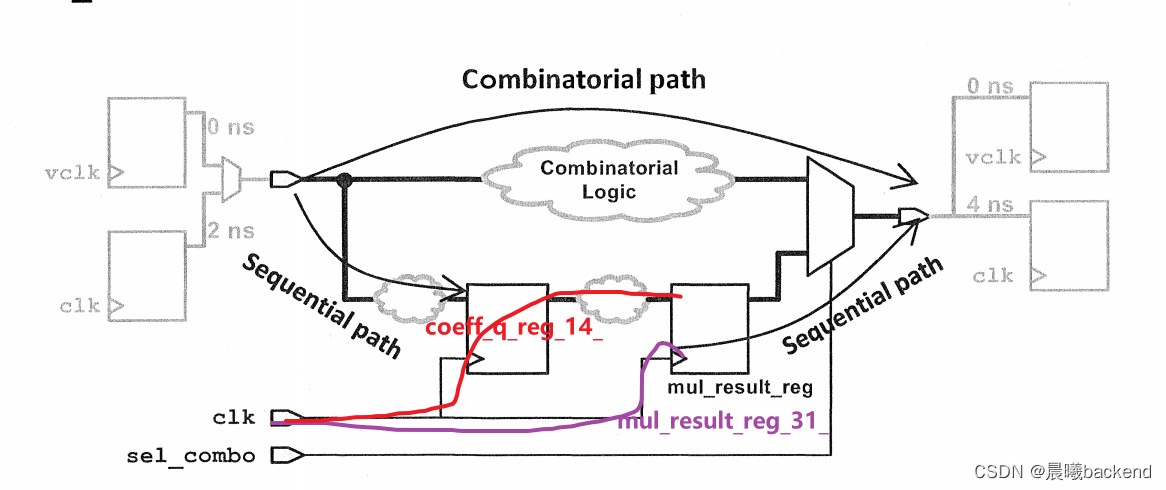
8.2 reg2reg
- 这里设置了
set_multicycle_path 2 -setup -to mul_result_reg*/D
8.3 reg2out
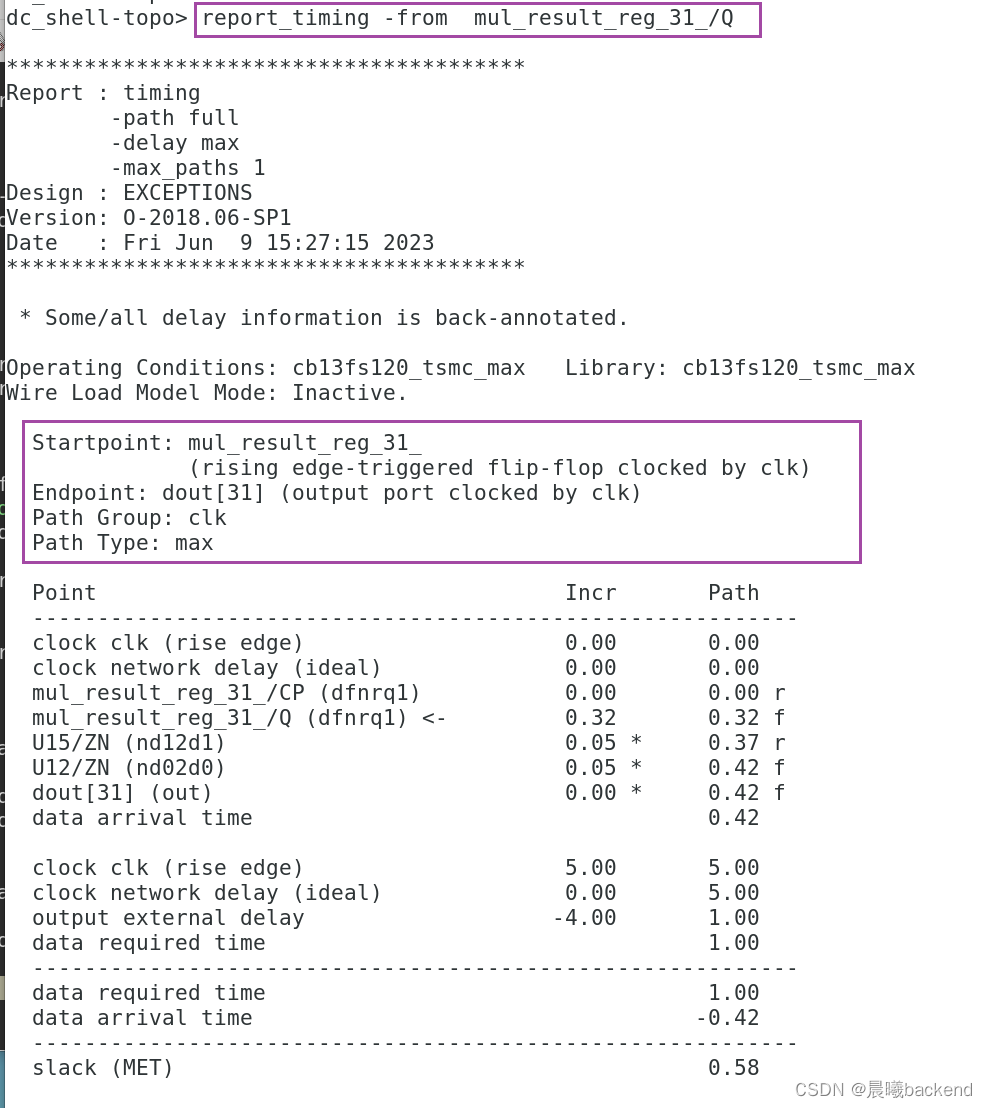
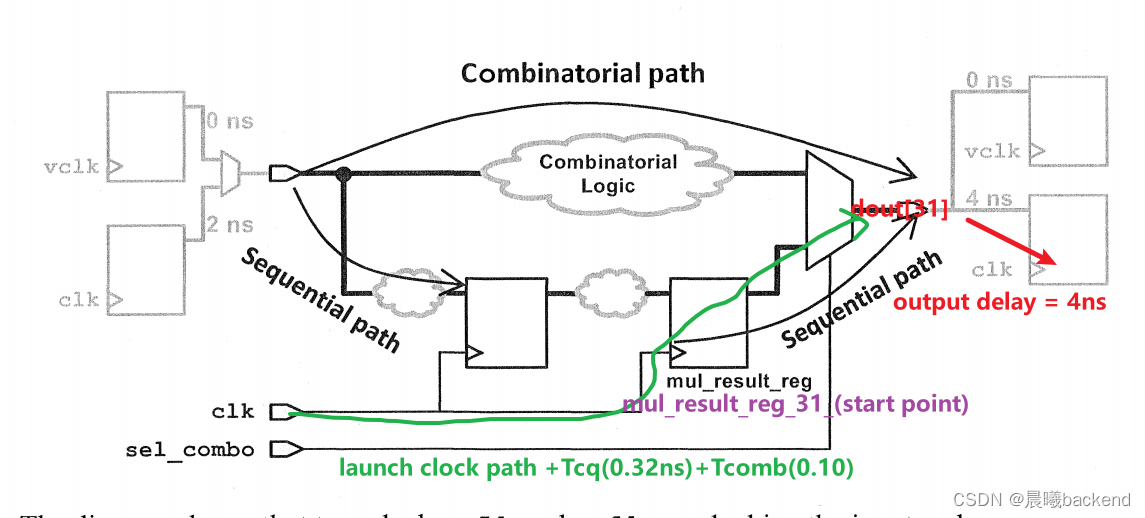
8.4 in2out
8.4.1 in2out(adr_i[0]-->dout[6]) demo
report_timing -from adr_* -to dout[6]
report_timing -from adr_* -to dout*
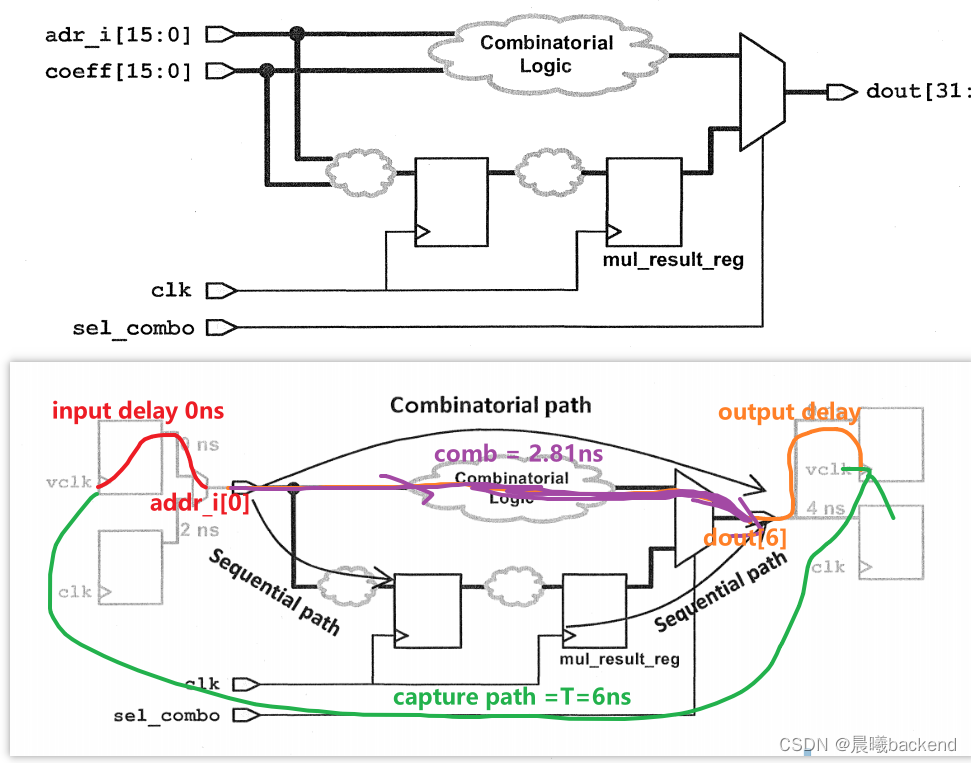
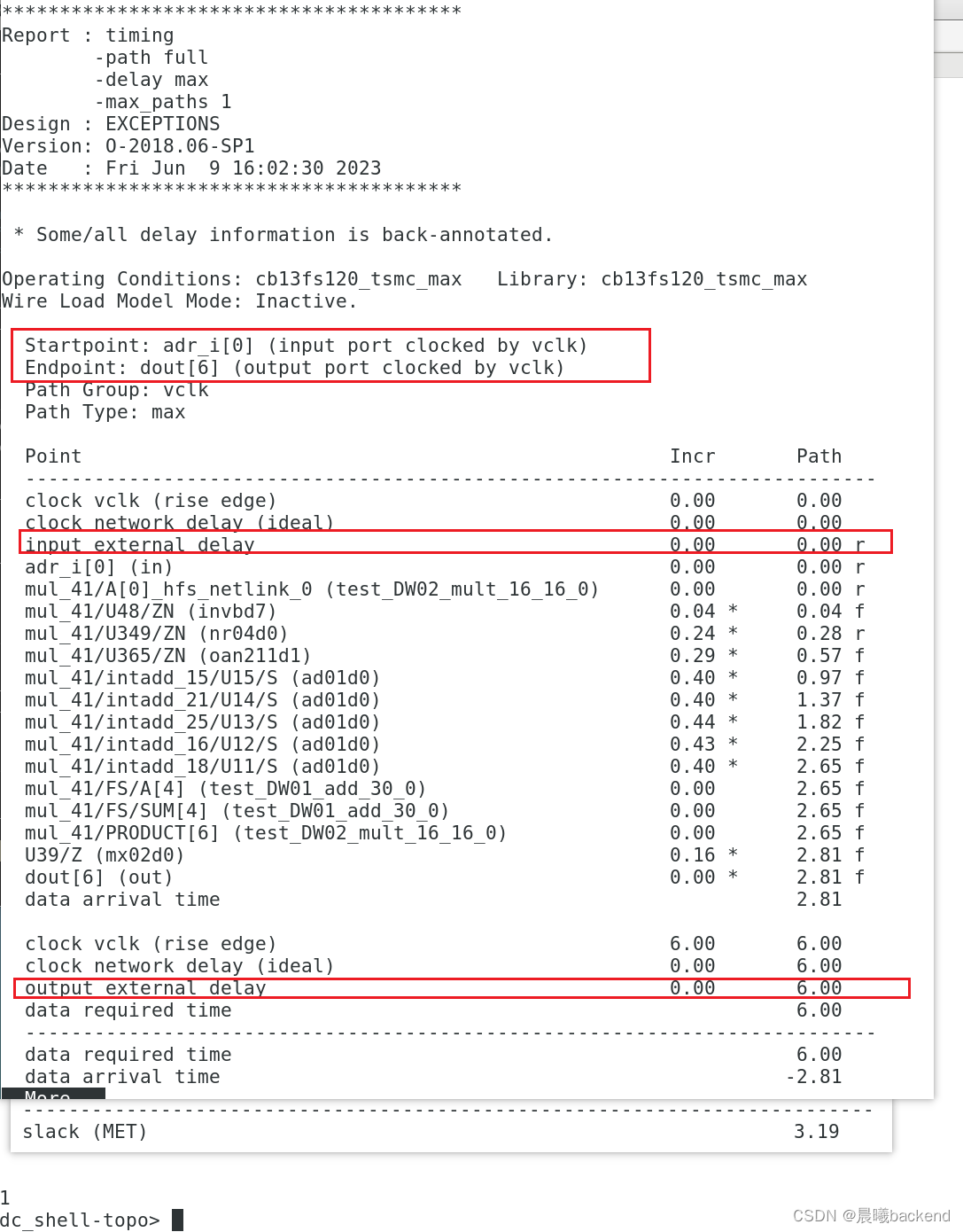
8.4.2 in2out(coeff[5]-->dout[6]) demo
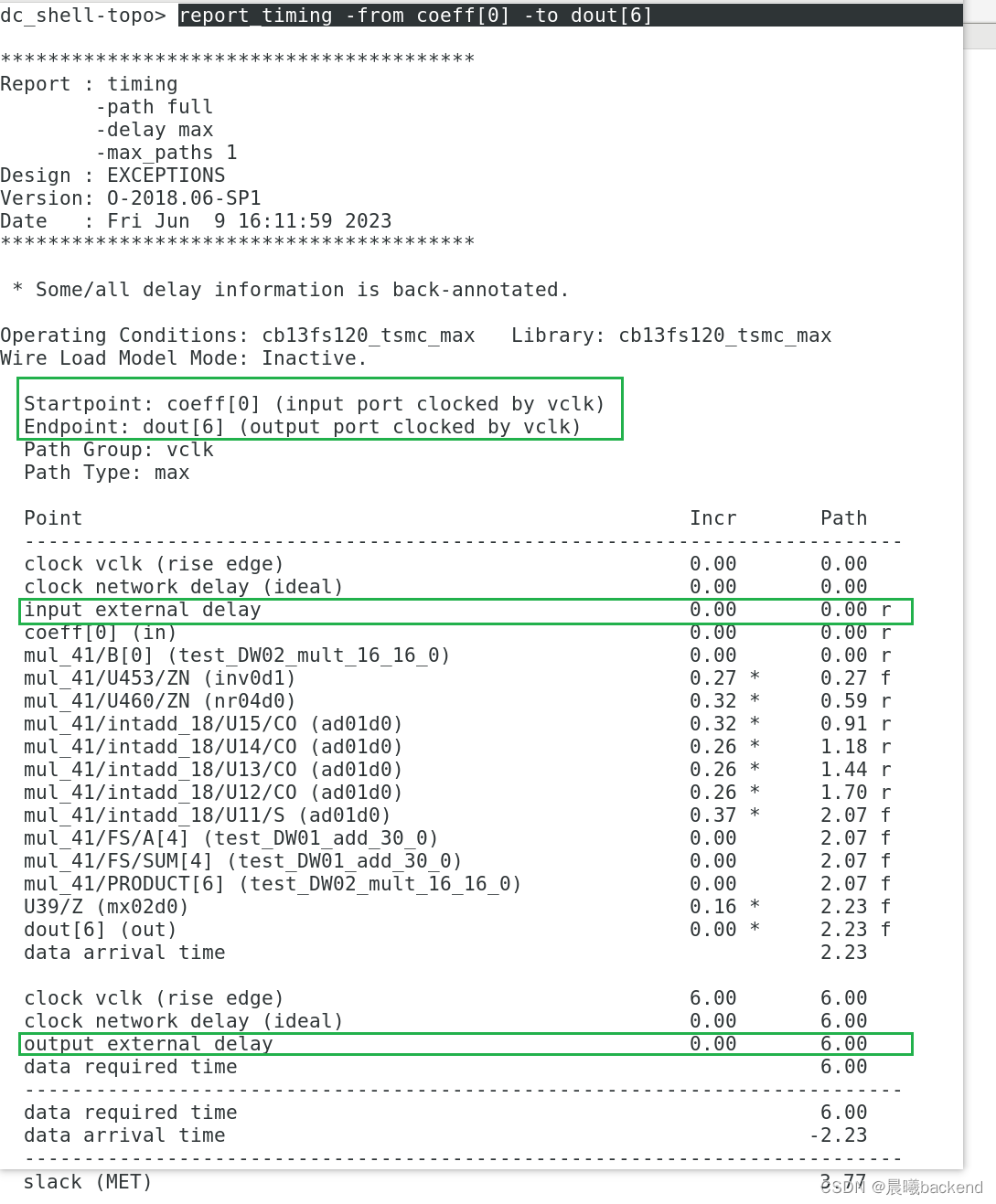
report_timing -from coeff* -to dout[6]
report_timing -from coeff[0] -to dout[6]
9.打印所有port、cells、pins
get_ports


get_cells

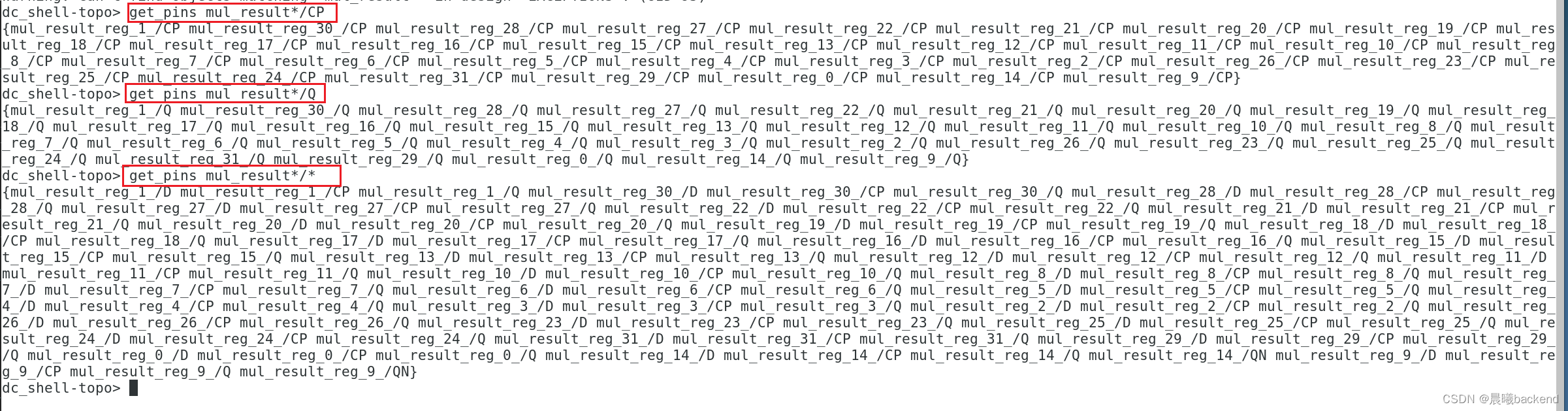
get_pins
相关文章:

DC LAB8SDC约束四种时序路径分析
DC LAB 1.启动DC2.读入设计3. 查看所有违例的约束报告3.1 report_constraint -all_violators (alias rc)3.2 view report_constraint -all_violators -verbose -significant_digits 4 (打印详细报告) 4.查看时序报告 report_timing -significant_digits 45. 约束组合逻辑(adr_i…...

学生考试作弊检测系统 yolov8
学生考试作弊检测系统采用yolov8网络模型人工智能技术,学生考试作弊检测系统过在考场中安装监控设备,对学生的作弊行为进行实时监测。当学生出现作弊行为时,学生考试作弊检测系统将自动识别并记录信息。YOLOv8 算法的核心特性和改动可以归结为…...

【基于容器的部署、扩展和管理】 3.2 基于容器的应用程序部署和升级
往期回顾: 第一章:【云原生概念和技术】 第二章:【容器化应用程序设计和开发】 第三章:【3.1 容器编排系统和Kubernetes集群的构建】 3.2 基于容器的应用程序部署和升级 3.2 基于容器的应用程序部署和升级 3.2 基于容器的应用程…...

Jmeter 实现 grpc服务 压测
一、Jmeter安装与配置 网上有很多安装与配置文章,在此不做赘述 二、Jmeter gRPC Request 插件安装 插件下载地址:JMeter Plugins :: JMeter-Plugins.org 将下载文件解压后放到Jmeter安装目录下 /lib/ext 然后在终端输入Jmeter即可打开 Jmeter GUI界面…...
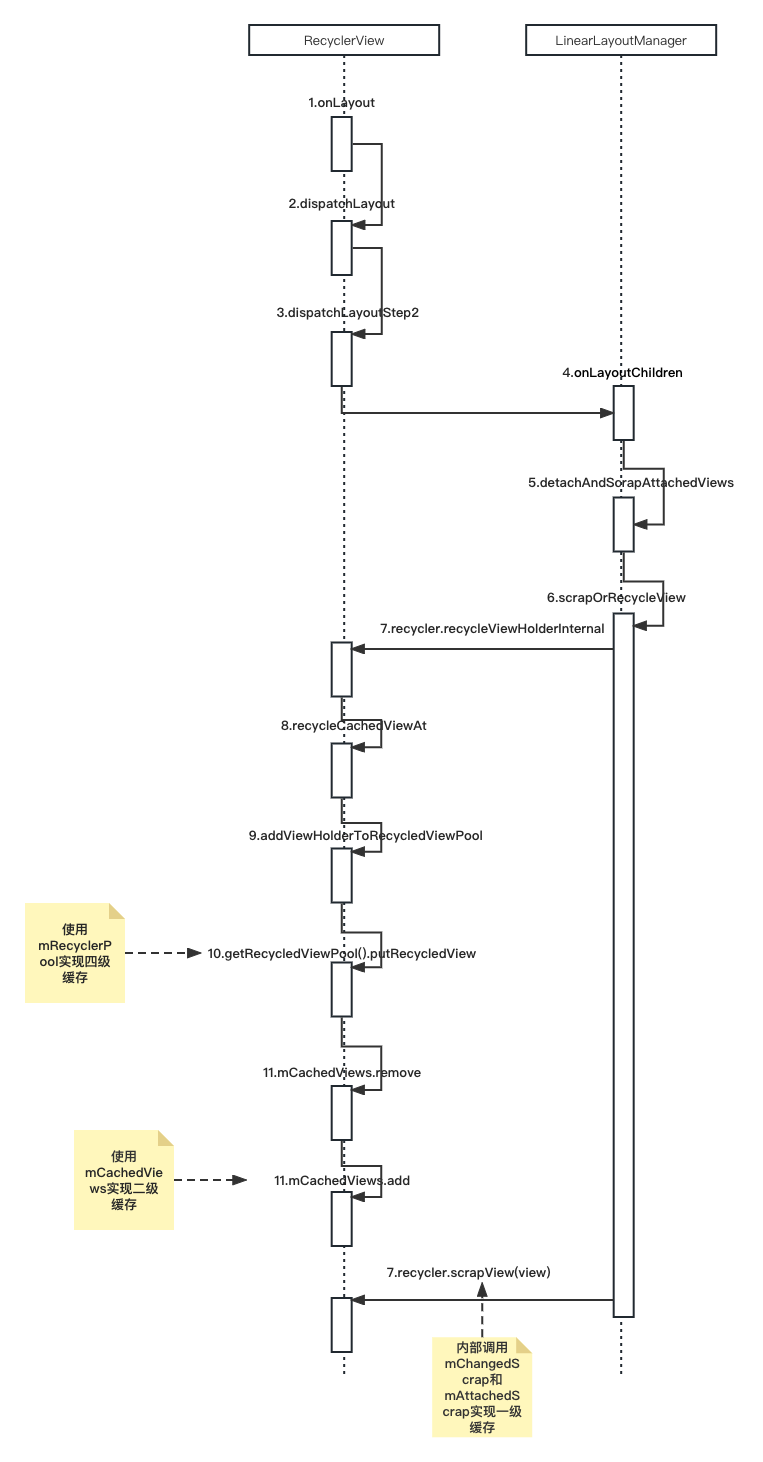
深入源码分析RecyclerView缓存复用原理
文章目录 前言四级缓存 源码分析缓存一级缓存(mChangedScrap和mChangedScrap)二级缓存(mCachedViews)三级缓存(ViewCacheExtension)四级缓存(mRecyclerPool)缓存池mRecyclerPool结构…...

内网隧道代理技术(一)之内网隧道代理概述
内网隧道代理技术 内网转发 在渗透测试中,当我们获得了外网服务器(如web服务器,ftp服务器,mali服务器等等)的一定权限后发现这台服务器可以直接或者间接的访问内网。此时渗透测试进入后渗透阶段,一般情况…...

设计图形用户界面的原则
1) 一般性原则:界面要具有一致性、常用操作要有快捷方式、 提供简单的错误处理、对操作人员的重要操作要有信息反馈、操作可 逆、设计良好的联机帮助、合理划分并高效地使用显示屏、保证信息 显示方式与数据输入方式的协调一致 2) 颜色的使用:颜色…...

1:操作系统导论
1.1操作系统的定义 •Anoperatingsystemactsanintermediarybetweenuserofacomputerandthecomputer hardware. ◦ 操作系统充当计算机⽤⼾和计算机硬件之间的中介 •Thepurposeofanoperatingsystemistoprovideanenvironmentinwhichausercanexecute programsinaconvenientandeff…...

什么是微软的 Application Framework?
我是荔园微风,作为一名在IT界整整25年的老兵,今天来看一下什么是微软的 Application Framework? 到底什么是 Application Framework? 还没有真正掌握任何一套Application Framework的使用之前,就来研究这个真的不是很…...

一个关于宏定义的问题,我和ChatGPT、NewBing、Google Bard、文心一言 居然全军覆没?
文章目录 一、问题重述二、AI 解题2.1 ChatGPT2.2 NewBing2.3 Google Bard2.4 文心一言2.5 小结 一、问题重述 今天在问答模块回答了一道问题,要睡觉的时候,又去看了一眼,发现回答错了。 问题描述:下面的z的值是多少。 #define…...

【服务器数据恢复】断电导致RAID无法找到存储设备的数据恢复案例
服务器数据恢复环境: HP EVA存储,6块SAS硬盘组建的raid5磁盘阵列。上层操作系统是WINDOWS SERVER。该存储为公司内部文件服务器使用。 服务器故障&分析: 在遭遇两次意外断电后,设备重启时raid提示“无法找到存储设备”。管理员…...
Windows上不可或缺的5款宝藏软件,工作效率拉满!
职场小白与大牛的区别:小白需要耗费大半天琢磨的事情,而大牛可以只花5分钟就能处理。 “牛人”,即拥有过人之处,专业、经验、技术等等,学会灵活运用高效率的工具也是关键的一点。工具找得好,运用得快&#…...
链表内指定区间反转
题目: 将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转,要求时间复杂度 O(n),空间复杂度 O(1)。 例如: 给出的链表为 1→2→3→4→5→NULL,m2,n4 返回 1→4→3→2→5→NULL 数据范围ÿ…...

Vue中如何进行地图展示与交互(如百度地图、高德地图)?
Vue中如何进行地图展示与交互 随着移动互联网的普及,地图应用已经成为人们生活中不可或缺的一部分。在Vue.js中,我们可以使用第三方地图库(如百度地图、高德地图)来实现地图的展示和交互。本文将介绍如何在Vue.js中使用百度地图和…...

uni-app组件概述
1、组件 1.1、组件的含义 组件是视图层的基本组成单元。 组件是一个单独且可复用的功能模块的封装。 组件,包括:以组件名称为标记的开始标签和结束标签、组件内容、组件属性、组件属性值。 <component-name>是开始标签,</compon…...

什么是防火墙?它有什么作用?
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 目录 一、什么是防火墙 二、防火墙的分类 1、软件防火墙 2、硬件防火墙 三、防火墙的作用 1、防止病毒 2、防止访问不安全内容 3、阻…...
基础工程(cubeide串口调试,printf实现,延时函数)
0.基础工程(cubeide串口调试,printf实现,延时函数) 文章目录 0.基础工程(cubeide串口调试,printf实现,延时函数)外部时钟源CLOCK(RCC)系统时钟SYS与DEBUG设置UART串口设置cubeide设置…...
大厂设计师都在用的9个灵感工具
每一件伟大的设计作品都离不开设计师灵感的爆发。设计师有很多灵感来源,比如精美的摄影图片、酷炫的网站设计、APP的特色功能、友好的用户体验动画,或者一篇文章。 设计师每天都需要收集灵感,把灵感收集当成日常生活。在这篇文章中ÿ…...

安全实现SpringBoot配置文件自动加解密
需求背景 应用程序开发的时候,往往会存在一些敏感的配置属性 数据库账号、密码第三方服务账号密码内置加密密码其他的敏感配置 对于安全性要求比较高的公司,往往不允许敏感配置以明文的方式出现。 通常做法是对这些敏感配置进行加密,然后在…...
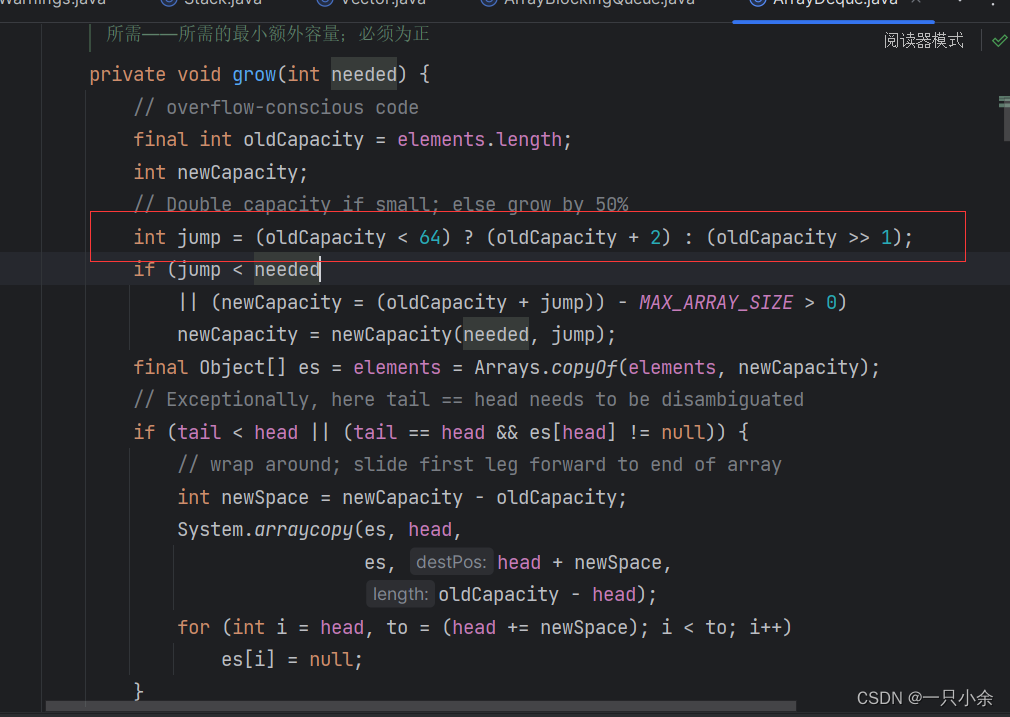
数据结构--队列2--双端队列--java双端队列
介绍 双端队列,和前面学的队列和栈的区别在于双端队列2端都可以进行增删,其他2个都是只能一端可以增/删。 实现 链表 因为2端都需要可以操作所以我们使用双向链表 我们也需要一共头节点 所以节点设置 static class Node<E>{E value;Node<E…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
