机器学习复习(上)
严正声明:本文的答案是ChatGPT的回答,仅供参考,不代表就是正确答案!!!
1.解释什么是过拟合和欠拟合,如何降低过拟合?
过拟合(overfitting)指的是一个模型在训练数据上表现很好,但在测试数据上表现不佳的现象。这是由于模型过于复杂,过度拟合训练数据,导致对新数据的泛化性能差。
欠拟合(underfitting)则指的是模型没有充分地学习训练数据中的模式和规律,因此在训练集和测试集上都表现不佳,泛化性能差。
为了解决这些问题,可以通过添加正则化项、采集更多的数据、提高模型复杂度或使用更好的特征工程等方法来改进模型,从而提高泛化性能。
以下是几种常用的方法来降低过拟合:
1. 数据增强:扩充训练数据集的方式来减轻过拟合。数据增强可以包括随机裁剪、随机旋转、随机缩放、翻转等操作,能够让模型学习到更多的不同变换的模式,增强泛化能力。
2. 正则化:加入L1、L2正则化项,或者使用Dropout等技术,以适度限制权重的大小,减少过拟合。
3. 增大训练集:采集更多的数据,可以使得模型更好地泛化到未见过的数据。
4. 参数调整:改变学习率、权重衰减系数等参数,可以让模型获得更好的性能。
5. 使用预训练模型:使用在大规模数据上训练的预训练模型作为模型的起点,再在小规模数据上进行微调,能够让模型更容易收敛,同时避免过拟合。
6. 提前停止训练:当出现验证集上的性能不再提升时,可以提前停止模型的训练,避免过拟合。
2.什么是10次10折交叉验证?
10次10折交叉验证(10-fold cross-validation)是一种模型评估方法,常用于评估机器学习模型的性能。它将原始数据集分为10份,每次将其中9份作为训练数据,1份作为测试数据,重复10次,每次都将不同的一份作为测试数据。这样可以获得10个独立的模型评估结果,可以对模型评估的稳定性和泛化能力进行充分评估。
具体步骤如下:
1. 首先将数据集分成10份(可以是随机分配或者按顺序分配)。
2. 选择一份作为测试集,其余9份作为训练集。
3. 在训练集上训练模型,并在测试集上评估模型的性能(可以通过计算准确率、F1-score等指标)。
4. 重复步骤2-3,直到所有的测试集都被用作了一次测试集。
5. 计算10次评估结果的平均值,作为模型的最终评估结果。
这种方法的优点在于,可以避免因为数据集划分不合理等原因导致的模型评估结果不准确的问题,并且可以最大化地利用数据,有效评估模型的性能。
为什么要这样设计?
10次10折交叉验证的设计是为了减少模型评估的偏差和方差。在一次固定的训练-测试集划分中,评估结果具有一定的随机性。如果只进行一次训练-测试集划分,评估结果可能受到这种随机性的影响,导致评估结果不稳定,不具备代表性。
10次10折交叉验证可以通过每次随机选择测试集,进行多次训练-测试集划分并评估,从而平均化随机的影响,减少评估结果的随机性,提高评估结果的稳定性和可信度,从而更加准确地评估模型的泛化能力。
另外,这种设计还可以最大化地利用数据,避免训练集和测试集样本不足或者不够充分的问题,从而更加充分地评估模型的性能。
3.什么是预剪枝和后剪枝?从时间开销、过拟合欠拟合风险,泛化性能等角度来讨论两种方式的差异。
预剪枝和后剪枝都是决策树中用来避免过拟合的技术,它们的主要区别在于剪枝的时间。
预剪枝是在生成决策树的过程中,在每个节点进行划分前,先通过计算信息增益或其他指标评估该节点是否需要进一步划分。如果该节点不满足预先设定的条件,那么就停止划分,将当前节点标记为叶子节点。
预剪枝优点在于节省了决策树的构建时间,同时降低了过拟合的风险。
但如果预先设定的条件不够准确,就容易出现欠拟合的情况。
后剪枝是在生成完整的决策树之后,再对决策树进行剪枝。方法是从叶子节点开始,逐个考察非叶子节点,判断若将其子节点合并是否可以提高决策树的泛化能力。如果合并后泛化误差没有显著增加,则将该节点及其子节点合并成一个叶子节点。
后剪枝优点在于不需要预先确定剪枝条件,可以更加充分地利用训练数据,同时也能够减小过拟合的风险。
后剪枝的缺点在于需要额外的计算开销,并且合并节点时可能会丢失某些重要特征,导致欠拟合的情况。
差异:
(1)从时间开销来看:
预剪枝时间开销小,因为是在训练时就规定决策树的最大深度或结点中的最小样本数等参数,避免了不必要的划分。
后剪枝需要在训练后进行模型修剪,时间开销相对较大。
(2)从过拟合与欠拟合的风险来看:
预剪枝能够有效避免过拟合,但可能无法充分利用所有的训练数据和特征;
后剪枝可以使用整棵树学习所有训练数据和特征,避免欠拟合,但存在在训练集上过拟合的风险。
(3)从泛化性能来看:
后剪枝的结果往往比预剪枝更优秀,因为树的结构更加灵活,可以更好地适应新的数据集和特征。但是,多次剪枝可能会导致树的模型更模糊,泛化能力下降。
4.什么支持向量?利用KKT条件分析硬间隔支持向量机的解具有稀疏性?
支持向量是指在支持向量机(SVM)模型中用来确定决策边界和分类超平面的样本点。在硬间隔支持向量机模型中,支持向量是距离分类超平面最近的那些点。这些点与分类超平面的距离称为支持向量到分类超平面的距离。
利用KKT条件可以对硬间隔支持向量机的解进行分析,判定哪些数据点是支持向量,哪些数据点不是支持向量,从而得到模型的稀疏性:
1. 对于每一个样本点,其对应的拉格朗日乘子alpha必须满足KKT条件,即alpha=0或者相应的约束条件等式成立。
2. 对于一些非支持向量,其对应的alpha值为0,不参与到求解分类超平面的过程中,所以在解决分类问题时可以忽略这些非支持向量,从而实现模型的稀疏化。
3. 在硬间隔SVM中,支持向量的数量往往比样本点总数要小得多,因此可以通过只考虑支持向量的方式来简化计算。
综上所述,利用KKT条件可以确定硬间隔支持向量机模型中的支持向量,并且可以将非支持向量忽略,从而实现模型的稀疏化。这种方法可以降低计算量,提高模型的训练和预测效率,并且减少了模型的复杂度,更容易进行可视化的展示。
5.简单描述下K-means聚类流程,该聚类算法的优点和缺点。
K-means聚类是一种常用的无监督学习算法,其流程如下:
1. 随机选择k个中心点作为初始质心,其中k为用户自定义的聚类数量。
2. 对于每一个样本点,计算其与k个中心点之间的距离,将样本点分配给最近的中心点所在的簇。
3. 对于每一个簇,重新计算其中所有样本点的均值,得到新的中心点。
4. 重复步骤2和步骤3,直到中心点不再发生改变或者达到预先设定的迭代次数。
K-means聚类算法的优点:
1. 算法简单,易于实现。
2. 当数据集较大时也可以运行得很快。
3. 对于密集型数据集效果较好,尤其是当k值相对较小且簇的形状比较规则时。
4. 能够应用于不同类型的数据,包括数值型、二元型和标称型等多种数据类型。
K-means聚类算法的缺点:
1. 用户需要提前设置聚类数量k,而这个值的选择可能会影响到聚类结果,同时该值不易确定。
2. 对初始质心的选择对聚类结果有影响,因此需要多次运行算法并选择最好的结果。
3. 当数据集中存在噪声或者离群点时,K-means聚类算法可能会受到影响。
4. 只能仅仅发现球状簇,而不能发现非球形簇或者具有复杂形状的簇。
精简版本:
1.聚类结果受初始聚类中心的影响较大,可能会陷入局部最优解;
2.对于非凸形状的聚类结构,聚类效果可能不理想;
3.不适用于聚类数量未知的情况。
综上所述,K-means聚类算法是一种简单有效的聚类算法,但在处理非球形簇或者噪声数据时存在一定的局限性。这种算法适用于对数据进行大致分类和聚类的场景,但对于对数据簇内的分布形态要求较高的场景不太适用。
6.什么是维数灾难?环节维数灾难的两大主流技术分别是什么?
维数灾难,也称“高维灾难”,是指当数据集的维度(特征数量)变得非常大时,会出现一些问题。具体而言,维数灾难可能导致数据变得非常稀疏、噪声数据的影响变得更加显著、距离计算变得更加困难、模型的复杂度和训练时间增加等问题。
在处理高维数据时,可以采用主流技术来解决维数灾难问题,包括:
(1)特征选择:特征选择是指从原始特征中选择有意义的子集作为新特征集合,以达到减少维度的目的。该方法可以保留最有用的特征,过滤掉无用甚至有害的特征。
(2)特征提取:特征提取是把原有的特征空间转换为一个新的特征空间,从而减少维度同时保留原有特征的有效信息。该方法可以通过降维方法、深度学习方法等实现对高维数据的有效处理。
综上所述,维数灾难是指当数据集维度变得非常大时,面临的各种问题。处理高维数据时,可以采取特征选择或者特征提取的方法来解决维数灾难问题。
7.在特征选择中,为什么L1范数能比L2范数获得稀疏解?
在特征选择中,L1范数和L2范数是两种常用的正则化方法,可以用于惩罚模型参数,从而实现特征选择和降维。
其中,L1范数和L2范数的主要区别在于所惩罚的系数不同,L1范数是绝对值之和,而L2范数是平方和后再开根号。
L1范数和L2范数的计算公式分别如下:
L1范数:||w||1 = |w1|+|w2|+…+|wn|
L2范数:||w||2 = sqrt(w1^2 + w2^2 + … + wn^2)
其中,w为特征权重。
在L1范数正则化中使用的优化算法(如Coordinate Descent)会让一部分模型参数变为0,从而实现了特征选择的效果。相比之下,L2正则化不会直接将某些模型参数变为0,仅仅是让模型参数变得很小。
L1正则化比L2正则化更适合处理稀疏性数据,因为在高维数据中,存在很多冗余或者无用的特征,这些特征对应的权重可以通过L1正则化让它们的系数归零,从而实现特征的筛选和降维。
在数学上,L1正则化使得目标函数具有局部的稀疏性,即只有少量的参数非零,而L2正则化不会产生类似的稀疏性,导致需要更多的参数来表示模型,从而可能过拟合。因此,L1范数比L2范数更适合于特征选择和稀疏表示问题。
如果考试挂科,并不负任何挂科责任!!!
最终解释权归isxhyeah所有!!!
相关文章:
)
机器学习复习(上)
严正声明:本文的答案是ChatGPT的回答,仅供参考,不代表就是正确答案!!! 1.解释什么是过拟合和欠拟合,如何降低过拟合? 过拟合(overfitting)指的是一个模型在训练数据上表…...

node笔记_express结合formidable实现前后端的文件上传
文章目录 ⭐前言⭐安装http请求的文件解析依赖库💖 安装 formidable💖 node formidable接受formData上传参数 ⭐上传的页面搭建💖 vue2 element upload💖 node 渲染 上传文件 ⭐后端生成api上传文件到指定目录💖完整的…...
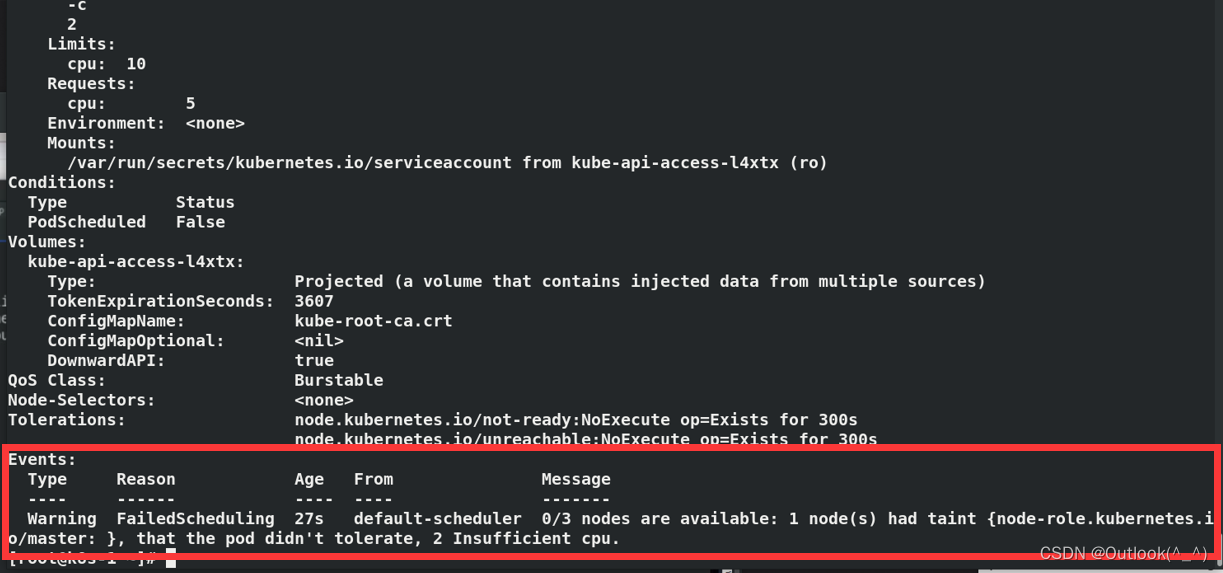
CKA 09_Kubernetes工作负载与调度 资源调度 三类QoS request 资源需求 limit 资源限额
文章目录 1. 资源调度1.1 准备工作1.2 为什么需要 request 和 limit1.3 内存限制1.3.1 Brustable1.3.2 Guaranteed1.3.3 BestEffort1.3.4 当容器申请的资源超出 limit 和 request 1.4 CPU限制 1. 资源调度 1.1 准备工作 Kubernetes 采用 request 和 limit 两种限制类型来对资源…...
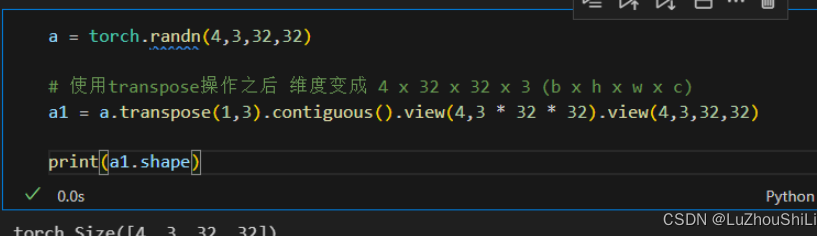
【pytorch】维度变换
【pytorch】维度变换 View操作unSqueeze操作图片处理的一个案例squeeze 维度删减操作维度扩展-expand维度扩展-repeat矩阵的转置操作-transpose View操作 将一个四维的张量(b x c x h x w)转换成一个二维的张量 对于四张图片 将每一张图像用一行向量进…...
)
vue3中的nextTick()
目录 nextTick() 方法用法回调函数方式使用await方式使用 实现原理使用nextTick() 方法时的注意事项 nextTick() 方法 nextTick() 方法是一个非常强大的工具,是一个等待下一次 DOM 更新刷新的工具方法。用于将一个函数以异步的方式推迟到下一个 DOM 更新周期执行。…...
高效学习传感器|霍尔式传感器
01、霍尔式传感器的工作原理 1●霍尔效应 霍尔式传感器的物理基础是霍尔效应。如图1所示,在一块长度为l、宽度为b、厚度为d的长方体导电板上,左、右、前、后侧面都安装上电极。在长度方向上通入电流I,在厚度方向施加磁感应强度为B的磁场。 ■…...
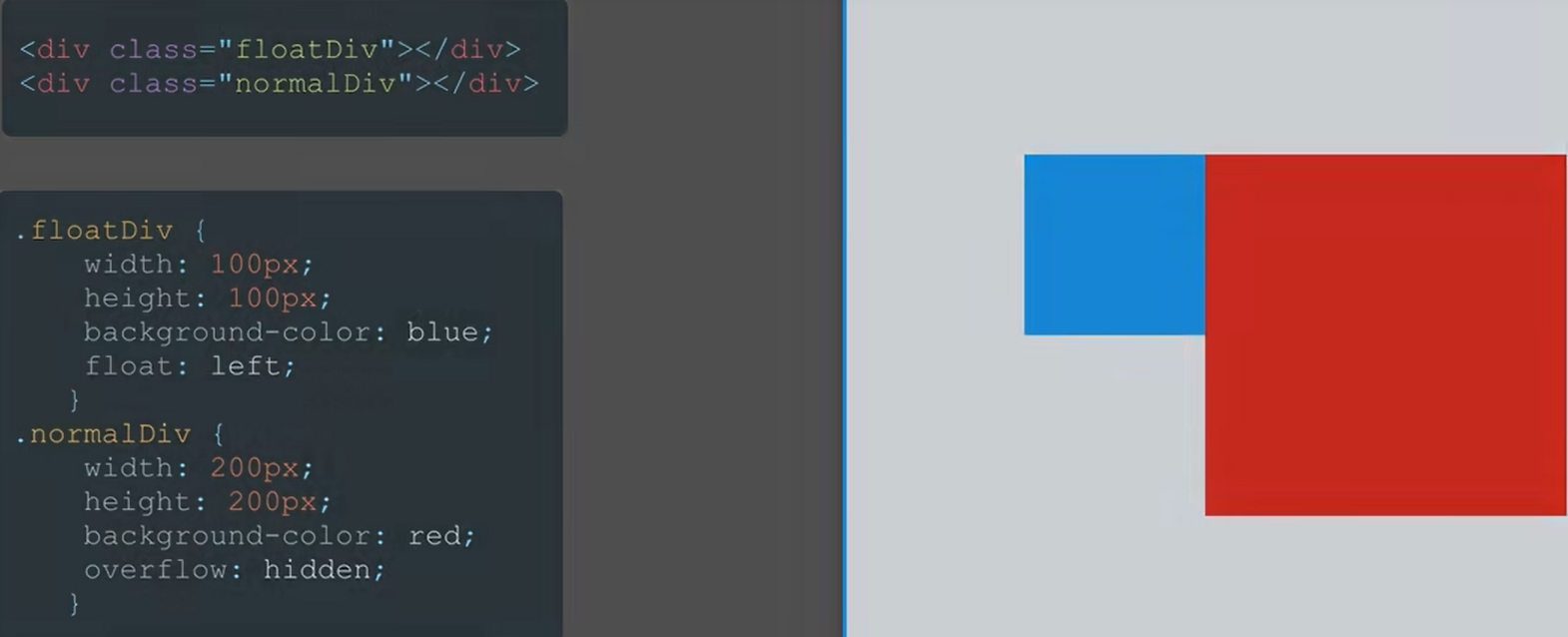
2023年前端面试高频考点HTML5+CSS3
目录 浏览器的渲染过程⭐⭐⭐ CSS 、JS 阻塞 DOM 解析和渲染 回流(重排)和重绘⭐⭐ 选择器 ID选择器、类选择器、标签选择器(按优先级高到低排序)⭐⭐ 特殊符号选择器(>,,~,空格࿰…...
企业开源测试项目实战(附全套实战项目教程+视频+源码)
接口测试项目 1. No matching distribution found for itypes1.1.0 Could not find a version that satisfies the requirement itypes1.1.0 (from -r requirements.txt (line 8)) (from versions: ) No matching distribution found for itypes1.1.0 (from -r requirements.…...

信创办公–基于WPS的EXCEL最佳实践系列 (创建表格)
信创办公–基于WPS的EXCEL最佳实践系列 (创建表格) 目录 应用背景操作步骤1、新建空白工作簿并命名为“奖牌榜”2、使用模板新建工作簿3、新增一张工作表,并将工作簿的标签更改为红色4、复制与隐藏工作表5、添加工作簿属性值6、更改工作簿主题…...
四、HAL_驱动机械按键
1、开发环境。 (1)KeilMDK:V5.38.0.0 (2)STM32CubeMX:V6.8.1 (3)MCU:STM32F407ZGT6 2、机械按键简介 (1)按键内部是机械结构,也就是内部是没有电路的。按键按下内部引脚导通,松开内部断开。 3、实验目的&原理…...
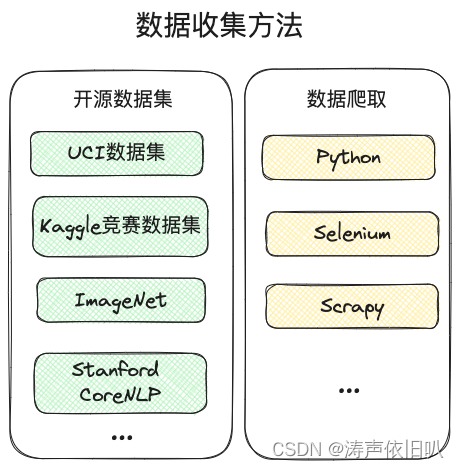
机器学习实战六步法之数据收集方法(四)
要落地一个机器学习的项目,是有章可循的,通过这六个步骤,小白也能搞定机器学习。 看我闪电六连鞭!🤣 数据收集 数据是机器学习的基础,没有数据一切都是空谈!数据集的数据量和数据的质量往往决…...

神经网络:CNN中的filter,kernel_size,strides,padding对输出形状的影响
输入数据在经过卷积层后,形状一般会发生改变,而形状的变化往往与以下四个超参数有关。 1,filter(out_channel) 该超参数控制着输入数据经过卷积层中需要与几个卷积核进行运算,而输入数据与每个卷积核进行…...
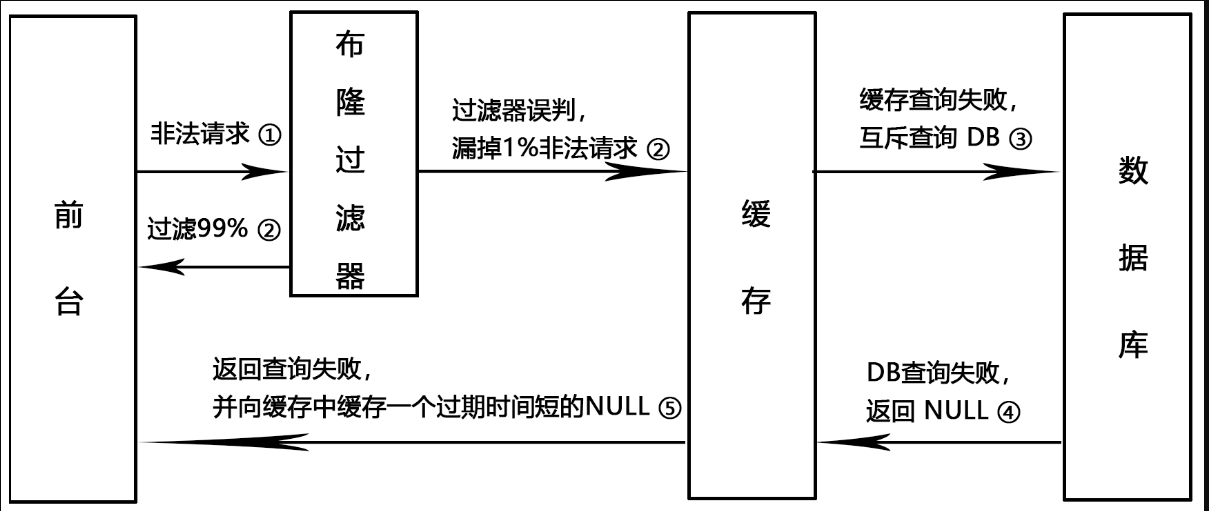
Spring Boot集成Redisson布隆过滤器案例
1 什么是布隆过滤器 布隆过滤器实际上是一个非常长的二进制向量(bitmap)和一系列随机哈希函数。那什么又叫哈希函数呢?哈希函数指将哈希表中元素的关键键值通过一定的函数关系映射为元素存储位置的函数。(HashMap源码) 布隆过滤器的优点&…...
使用 VSCode SSH 公网远程连接本地服务器开发 - cpolar内网穿透
文章目录 前言视频教程1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 转…...
portraiture宿主插件最新v4中文版本下载及使用教程
自拍怎么可以不修图呢?如果要修图的话,磨皮就是其中非常重要的一环。皮肤看起来细腻光滑了,整个人的颜值都会瞬间拉高。下面就让我们介绍一下磨皮用什么软件好用,什么软件可以手动磨皮的相关内容。portraiture是ps人像修图中常用的…...

一. ATR技术指标的定义与运用
一. ATR的定义 1. 什么是ATR ATR英文全名是Average true range,翻译过来就是平均真实波幅,这个指标主要用来衡量最近N天TR(真实波幅)的平均值。 2. ATR相关计算公式 T R [ ( 最高价 − 最低价 ) , ( 前一次收盘价 − 最高价 ) ࿰…...

linux find帮助文档
以下是完整的find命令帮助文档: 用法:find [-H] [-L] [-P] [-D debugopts] [-Olevel] [起始路径…] [表达式] 选项: -H 跟随命令行符号链接 -L 跟随所有符号链接 -P 不跟随任何符号链接(默认) -D debugopts 调试标志…...

搜索与图论(acwing算法基础)
文章目录 DFS排列数字n皇后 BFS走迷宫 拓扑序列单链表树与图的深度优先搜索模拟队列有向图的拓扑序列 bellman-ford有边数限制的最短路 spfaspfa求最短路spfa判断负环 FloydFloyd求最短路 PrimPrim算法求最小生成树 KruskalKruskal算法求最小生成树 染色法判定二分图染色法判定…...

【数据结构】何为数据结构。
🚩 WRITE IN FRONT 🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四" 🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2022博客之星T…...

【P57】JMeter 保存响应到文件(Save Responses to a file)
文章目录 一、保存响应到文件(Save Responses to a file)参数说明二、准备工作三、测试计划设计 一、保存响应到文件(Save Responses to a file)参数说明 可以将结果树保存到文件 使用场景:当结果太大,使…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
