CSDN竞赛57期题解
总结
交卷时一看才六十多分还有点吃惊,一看非编程题部分还是丢了二十分。填空题是这类竞赛最大的诟病,答案是名词的必然不唯一,答案需要计算的给定的参考答案必然计算错误,更离谱的是题目出成这样,反馈后官方竟然一点改变的意思都没有。但凡答案不唯一的题目你给多个候选答案也不会被人这么吐槽了。寄存器与状态寄存器、图灵机与图灵机模型这种不唯一的答案还记忆犹新,多少期前反馈时,C站不想着手动改一下判错的答案,而是回复以后不会再出填空题了,然而仅隔了一期填空题又再现了。
为什么这类竞赛的赞助商这么钟爱填空题呢?比如这次填空题答案是BST,看到题目时候我就在群里艾特出题人,BST至少有三种中文叫法,你想让我们填哪种?还特地翻了下书,没找着书上的叫法,于是在二叉搜索树、二叉排序树、二叉查找书当中选了个最常见的二叉搜索树填上去了,果不其然答案是二叉排序树,十分丢失。
另一道扣分的是判断题,问树的等价二叉树是不是唯一的,我寻思按照正常的转换方法应该是唯一的,结果却不是。失分的两题在书上也都没翻到解答。回到开始的问题,为什么赞助商总是出这种让人反感的填空题,他们的回复是以书上答案为准。提供了赞助,用这种方式迫使我们买本书不过分吧。还是随遇而安,叫不醒装睡的人,能白嫖本书也不亏。
编程题部分几乎该类竞赛每期都出现了不给数据规模的情况,可以发现出题人相当的不专业,python选手用map切分下就好了,C++选手每次写之前还要手动处理下输入数组,很是烦人。另外这次的两道题都不给数据范围,全靠自己猜范围了。
题目列表
1.凑数
题目描述
给定一组n个正整数,要求每次选其中一个数乘以或除以一个素数(称为一次凑数),问至少需要凑数多少次可以把所有的数都凑成相等。
分析
将所有数凑成相等第一反应是凑成最小公倍数或者最大公约数。但是这种方式的解很容易被推翻,比如2 4 8,凑成2和8的操作次数都是3,但是凑成4的次数是2,那么4这个数有什么性质呢?显然作为最终凑成的数,数组中小于它的数一定是它的约数,大于它的数一定是它的倍数。所以我们可以暴力求解一波,先列出一波候选解,除了数组里每个元素,还有就是它们的最大公约数和最小公倍数。可以先打表求出正向前 i i i个元素的最小公倍数 x x x以及逆向后 n − i n - i n−i个元素的最大公约数 y y y,如果 x x x 能被 y y y整除就尝试将 x x x和 y y y作为候选解求下凑的次数,最后取个最小值就可以了。
当然比赛时我没有这么做,秉着最大得分原则,读完题就想着先混个部分分,求出所有数的最大公约数 t t t,然后求所有数到 t t t需要操作的次数之和。提交通过了大部分用例,数据范围改到十万再提交就AC了,可见这个题目的数据还是比较水的,有点数论基础的同学都可以比较快的AC。
代码
#include <iostream>
#include <string>
using namespace std;
int a[100005];
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}
int get(int n) {int res = 0;for(int i = 2; i <= n; i++) {while(n % i == 0) {n /= i;res++;}}return res;
}
int main() {string s;getline(cin,s);int n = 0;int t = 0;int sz = s.size();for(int i = 0; i < sz; i++) {if (s[i] != ' ') t = t * 10 + s[i] - '0';else {a[n++]=t;t = 0;}}a[n++] = t;t = a[0];for (int i = 1; i < n; i++) {t = gcd(t, a[i]);}int res = 0;for(int i = 0; i < n; i++) {int r = a[i] / t;res += get(r);}cout<<res<<endl;return 0;
}
2.树的寻路
题目描述
给定一棵有n个节点且节点编号为1到n的树,求满足以下条件的路径组合数: 1. 从节点a到节点b的路径(称为路径ab) 边数为p 2. 从节点c到节点d的路径(称为路径cd)边数为q 3. 路径ab和cd不交,即不存在一个节点既在路径ab又在路径 cd上
分析
这类题目早几年做应该是可以秒掉的,工作躺平太久加之下班比较困了,花了挺长时间才通过四成用例。首先题目用例给了三条边,结果是8,没有用例说明还是让人很疑惑的,毕竟组合数这个词比较模糊。用例是1到2,2到3,3到4这三条边,乍一看不就1-2和3-4这两个长度为1的边不相交嘛,就算再倒过来算上3-4和1-2也才两种组合数啊,8是怎么得到的?不妨尝试去枚举一下路径的起点,第一条路径的起点可以是1 2 3 4,可以得到以下的路径组合:
- 1-2,3-4
- 1-2,4-3
- 2-1,3-4
- 2-1,4-3
- 3-4,1-2
- 3-4,2-1
- 4-3,1-2
- 4-3,2-1
虽然看起来这些组合有点离谱,就两条路径弄出了八个组合,但是用例来看应该就是这种组合方式了。
想象一下作为一棵树,其中的任意一个节点作为路径的起点,路径可以向其孩子节点延伸,也可以向其祖先节点延伸,也可以通过祖先节点向其兄弟、表兄弟节点延伸,我们选定一个根节点来遍历是没有什么意义的。
不妨先建个图,然后像上面枚举路径起点那样去枚举路径长度为 x x x路径的起点,遍历到其中一条长度为 x x x的路径的终点时,要保证遍历途中的节点做好了标记。再遍历下所有节点,只要没被标记的节点都可以作为与长度为 x x x路径不相交的、长度为 y y y的路径的起点。再次以新的起点去遍历相邻节点,直到找到与第一条路径不相交的路径,就将方案数加上1。
dfs过程中要注意遇见被标记的节点不可继续拓展,因为要么是第二条路径遍历的时候遇见的第一条路径上的节点,要么就是父节点,从 a a a走到 b b b,显然不能再走回来了。
这题没有给定数据范围,比赛时就假定数据范围是1w了,题目评测是一旦有超时的用例就是TLE,一分没有。所以加了下数据规模超过一千的就输出0。当然直接输出0也能得到一成的分数。比赛时由于时间关系没有继续调整数据范围和TLE的界限的,不然应该可以通过更多的用例。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10005, M = 2 * N;
int idx = 0,e[M],ne[M],h[N];
int n,x,y,ans = 0;
int st[N];
void add(int a,int b) {e[idx]=b, ne[idx]=h[a],h[a] = idx++;
}
void dfs(int u, int d, int t) {if (!t) {//枚举的是第一条路径if (d == x) {//路径长度达到xfor(int i = 1; i <= n; i++) {if (!st[i]) {//枚举第二条路径的起点st[i] = true;dfs(i, 0, 1);st[i] = false;}}return;}} else {//枚举的是第二条路径if (d == y) {//第二条路径长度达到yans++;return;}}for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];//已经被标记的节点跳过if (st[j]) continue;st[j] = true;dfs(j, d + 1, t);st[j] = false;}
}
int main() {cin>>n>>x>>y;memset(h,-1,sizeof h);for(int i = 1; i < n; i++) {int a,b;cin>>a>>b;add(a,b);add(b,a);}if (n > 1000) {cout<<0<<endl;return 0;}for(int i = 1; i <= n; i++) {st[i] = true;//枚举长度为x的路径起点idfs(i, 0, 0);st[i] = false;}cout<<ans<<endl;return 0;
}
相关文章:

CSDN竞赛57期题解
总结 交卷时一看才六十多分还有点吃惊,一看非编程题部分还是丢了二十分。填空题是这类竞赛最大的诟病,答案是名词的必然不唯一,答案需要计算的给定的参考答案必然计算错误,更离谱的是题目出成这样,反馈后官方竟然一点…...
springboot+vue.js大学生竞赛报名作品评分管理系统
本文介绍了大学生竞赛管理系统的开发全过程。通过分析大学生竞赛管理系统管理的不足,创建了一个计算机管理大学生竞赛管理系统的方案。文章介绍了大学生竞赛管理系统的系统分析部分,包括可行性分析等,系统设计部分主要介绍了系统功能设计和数…...

Python爱好者的自我修养(1):简单输入与输出
Python简单输入与输出 1.输出1.1 简单输出1.2 转义字符1.2.1 定义1.2.2 常见的转义字符用法 2.输入3.温馨提示 终于…… 终于…… 我开始玩Python了 (不是C不学了哈,C还是照更~) 今天先来简单讲下输入和输出 1.输出 1.1 简单输出 输出的函…...
java SSM 摄影作品网站myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM 摄影作品网站系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代 码和数据库,系统主要采…...

[Maven高级]->近万字文章带你深入了解Maven
⭐作者介绍:大二本科网络工程专业在读,持续学习Java,努力输出优质文章 ⭐作者主页:逐梦苍穹 ⭐所属专栏:JavaEE ⭐如果觉得文章写的不错,欢迎点个关注一键三连😉有写的不好的地方也欢迎指正&…...

物联网Lora模块从入门到精通(五)光照与温湿度传感器
一、前言 在程序开发中,光照与温湿度的获取是十分常见与重要的,本文我们主要是使用M21温湿度光照三合一传感器,其中温湿度数据通过协议获取,而光照通过ADC获取。 二、代码实现 本文内容较为简单,且后续文章将在本文基…...

【网络编程】计算机网络基础知识总结 | 运输层 |TCP协议
文章目录 前言一、计算机网络层次结构二、网络层三、运输层3.1、TCP/IP协议介绍3.2、端口(协议端口号)3.3、套接字3.4、TCP实现原理3.4.1、TCP的特点3.4.2、停止等待协议3.4.3、滑动窗口协议3.4.4、拥塞控制3.4.5、TCP连接的三个阶段 3.5、UDP实现原理 前…...

python关键知识点
1. 变量:在程序中存储值或对象的名称。 2. 数据类型:指变量的数据类型,例如 str、int、float、list、tuple、dict、set 等。 3. 操作符:表示运算符号,例如加号 和减号 -。 4. 循环:通过重复执行某个代码…...

c# 从零到精通 数组的操作-将两个一维数组合并成一个二维数组
c# 从零到精通 数组的操作-将两个一维数组合并成一个二维数组 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Test07 { class Program { static void Main(string[] args) { //定义两个一维数组 int[] arr1 new int[] {…...
Linux目录结构(与window目录结构对比+绝对路径和相对路径)
一、Linux目录结构 Linux目录结构是一个标准化的文件系统层次结构,非常有组织性并且易于管理。而与Windows 操作系统不同,Linux将所有文件和设备都组织在一个单一的根目录下。以下是Linux的标准目录结构: /:根目录,包含…...
投票活动小程序开发搭建
由于小程序是基于微信开发者工具编写的,因此我先介绍一下需要使用的工具和技术: - 微信开发者工具:用于开发、调试和发布小程序。 - 小程序云开发:用于存储数据和进行后端逻辑处理。 - uni-app框架:uni-app 是一个使…...

代码随想录day18
513.找树左下角的值 本题用前中后序都可以(都是先遍历左再遍历右,保证最后一定是左侧的节点),因为没有中节点的处理逻辑,用全局变量记录最大深度,只要遇到叶子结点并且当前深度比最大深度大,就更…...
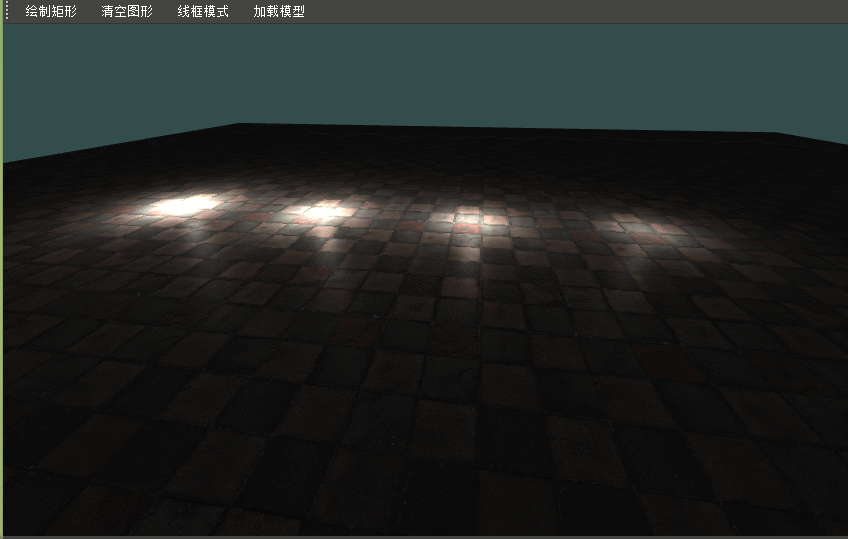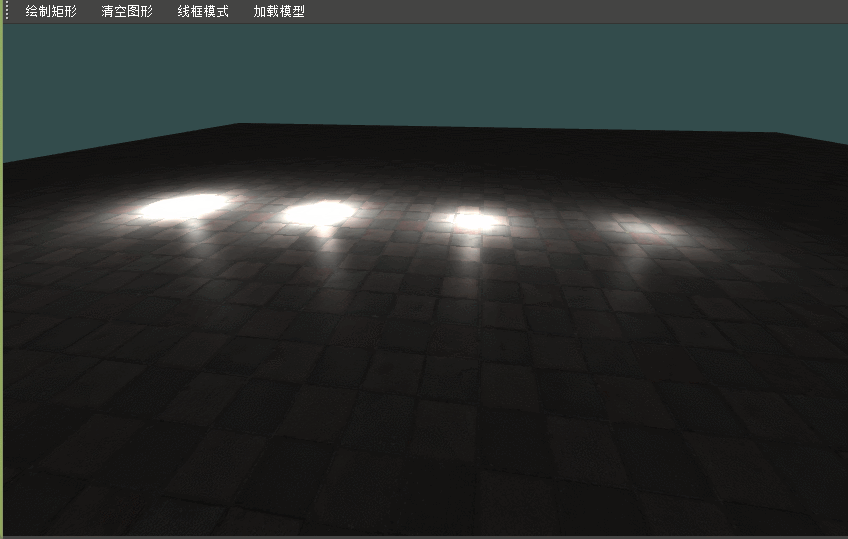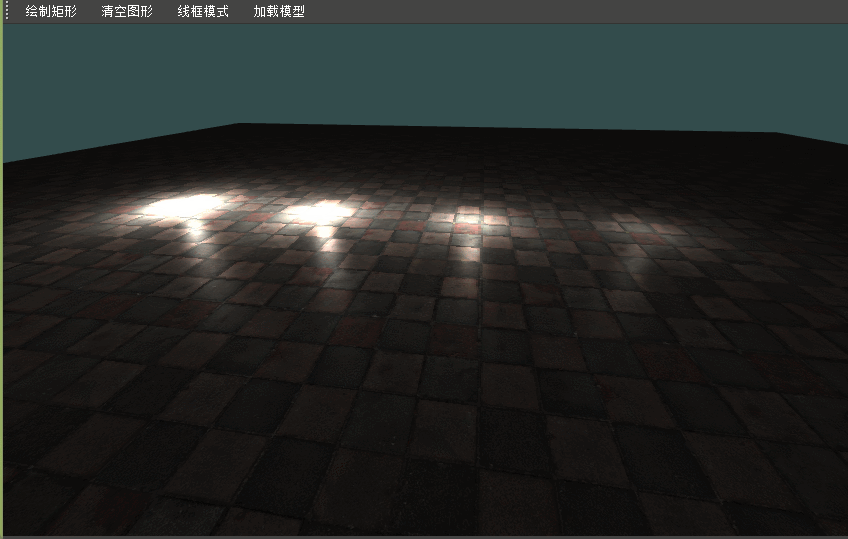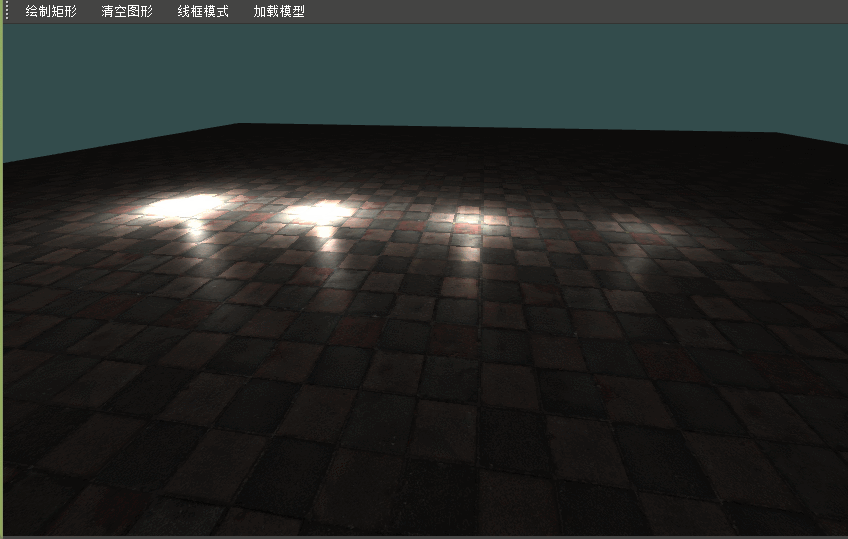
QT+OpenGL高级光照 Blinn-Phong和Gamma校正
QTOpenGL高级光照1 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 Blinn-Phong 冯氏光照:视线与反射方向之间的夹角不小于90度,镜面光分量会变成0.0(不是很合理&am…...
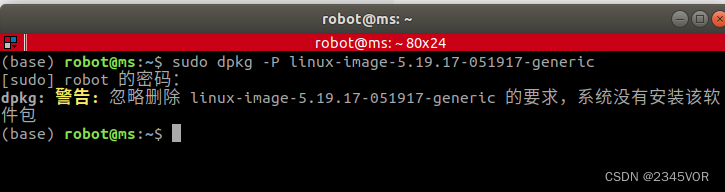
【Ubuntu系统内核更新与卸载】
【Ubuntu系统内核更新与卸载】 1. 前言2. 内核安装2.1 系统更新2.2 官网下载 3. 内核卸载3.1 需求分析3.2 卸载方法 1. 前言 我们在搭建环境时常常遇到内核版本不匹配的问题,需要我们安装新的内核版本;有时又会遇到在安装软件时报错boot空间已满无法安装…...
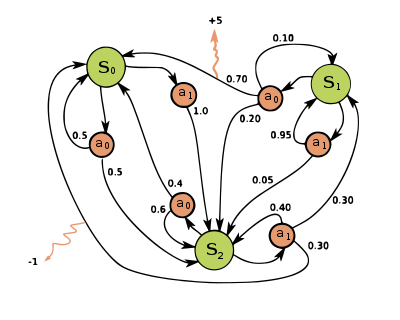
RL - 强化学习 马尔可夫奖励过程 (MRP) 的状态价值
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/131084795 GitHub 源码: https://github.com/SpikeKing/Reinforcement-Learning-Algorithm 马尔可夫奖励过程 (MRP) 的状态价值是指在某…...

Mybatis之批处理流式查询
文章目录 1 批处理查询1.1 引言1.2 流式查询1.2.1 定义1.2.2 流式查询接口1.2.3 使用流式查询关闭问题1.2.3.1 SqlSessionFactory1.2.3.2 TransactionTemplate1.2.3.3 Transactional 注解 1.2.4 完整示例1.2.4.1 mapper接口和SQL1.2.4.2 Service操作 1.3 游标查询1.3.1 定义1.3…...
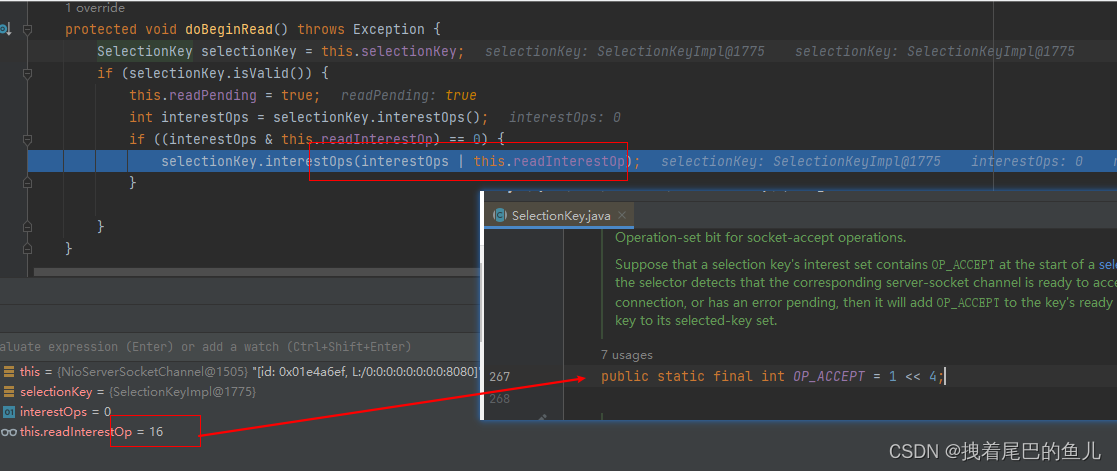
Spring架构篇--2.7.3 远程通信基础--Netty原理--bind实现端口的绑定
前言:在对ServerBootstrap 进行属性赋值之后,通过bind 方法完成端口的绑定,并开始在NioEventLoop中进行轮询进行事件的处理;本文主要探究ServersocketChannel 在netty 中是如何完成注册,以及端口的绑定 1 Nio selecto…...

【改进的多同步挤压变换】基于改进多同步挤压的高分辨率时频分析工具,用于分析非平稳信号(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

有关 python 切片的趣事
哈喽大家好,我是咸鱼 今天来讲一个我在实现 python 列表切片时遇到的趣事 在正式开始之前,我们先来了解一下切片(slice) 切片操作是访问序列(列表、字符串…)中元素的另一种方法,它可以访问一…...

ChatGPT 会带来失业潮吗?
(永久免费,扫码加入) 最近在翻知乎上的一些文章,很多都是跟ChatGPT有关的。因为本身是搞Python编程的,知乎推荐系统给我推荐了一篇廖雪峰老师的文章,觉得很有意思。 一共1119个赞,还是很厉害的&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

边缘计算设备全解析:边缘盒子在各大行业的落地应用场景
随着工业物联网、AI、5G的发展,数据量呈爆炸式增长。但你有没有想过,我们生成的数据,真的都要发回云端处理吗?其实不一定。特别是在一些对响应时间、网络带宽、数据隐私要求高的行业里,边缘计算开始“火”了起来&#…...

LeetCode 2894.分类求和并作差
目录 题目: 题目描述: 题目链接: 思路: 思路一详解(遍历 判断): 思路二详解(数学规律/公式): 代码: Java思路一(遍历 判断&a…...
