【运筹优化】最短路算法之A星算法 + Java代码实现
文章目录
- 一、A星算法简介
- 二、A星算法思想
- 三、A星算法 java代码
- 四、测试
一、A星算法简介
A*算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。
二、A星算法思想
A星(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是许多其他问题的常用启发式算法。注意——是最有效的直接搜索算法,之后涌现了很多预处理算法(如CH),在线查询效率是A*算法的数千甚至上万倍。
A*算法通过下面这个函数来计算每个节点的优先级, f ( n ) f(n) f(n) 越小,状态 n n n 被选择的优先级就越大:
公式表示为: f ( n ) = g ( n ) + h ′ ( n ) f(n)=g(n)+h'(n) f(n)=g(n)+h′(n),
- f ( n ) f(n) f(n) 是从初始状态经由状态 n n n 到目标状态的最小代价估计,
- g ( n ) g(n) g(n) 是在状态空间中从初始状态到状态 n n n 的最小代价,
- h ′ ( n ) h'(n) h′(n) 是从状态 n n n 到目标状态的路径的最小估计代价。(对于路径搜索问题,状态就是图中的节点,代价就是距离)
假设 h ( n ) h(n) h(n) 为状态 n n n 到目标状态的路径的最小真实代价。
则保证找到最短路径(最优解的)条件,关键在于估价函数 f ( n ) f(n) f(n) 的选取(或者说 h ′ ( n ) h'(n) h′(n) 的选取)。
以 h ′ ( n ) h'(n) h′(n) 表达状态 n n n 到目标状态估计的距离,那么 h ′ ( n ) h'(n) h′(n) 的选取大致有如下三种情况:
- 如果 h ′ ( n ) < h ( n ) h'(n)< h(n) h′(n)<h(n) ,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。
- 如果 h ′ ( n ) = h ( n ) h'(n)=h(n) h′(n)=h(n) ,此时的搜索效率是最高的。
- 如果 h ′ ( n ) > h ( n ) h'(n)>h(n) h′(n)>h(n) ,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
三、A星算法 java代码
@Data
public class AStar {// 0是路 1是墙 2是起点 3是终点private int[][] map;// 起点坐标int startI;int startJ;// 终点坐标int endI;int endJ;public AStar(int[][] map) {this.map = map;// 获取起点和终点坐标for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[i].length; j++) {if(map[i][j]==2){startI = i;startJ = j;}if(map[i][j]==3){endI = i;endJ = j;}}}}public void solve(){boolean[][] active = new boolean[map.length][map[0].length];PriorityBlockingQueue<Node> priorityBlockingQueue = new PriorityBlockingQueue<>();// 从起点出发ArrayList<int[]> initPath = new ArrayList<>();initPath.add(new int[]{startI,startJ});priorityBlockingQueue.add(new Node(startI,startJ,initPath,caculateDistance(startI,startJ)));active[startJ][startJ] = true;// 开始循环while (!priorityBlockingQueue.isEmpty()){Node node = priorityBlockingQueue.poll();if(node.getI()==endI && node.getJ()==endJ){for (int[] p : node.getPath()) {System.out.println(Arrays.toString(p));}System.out.println("最短路长度为:"+node.getPath().size());break;}// 向四周进行扩充// 上int i1 = node.getI()-1;int j1 = node.getJ();if(isAble(i1,j1,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i1,j1});priorityBlockingQueue.add(new Node(i1,j1,path,caculateDistance(i1,j1)));active[i1][j1] = true;}// 下int i2 = node.getI()+1;int j2 = node.getJ();if(isAble(i2,j2,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i2,j2});priorityBlockingQueue.add(new Node(i2,j2,path,caculateDistance(i2,j2)));active[i2][j2] = true;}// 左int i3 = node.getI();int j3 = node.getJ()-1;if(isAble(i3,j3,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i3,j3});priorityBlockingQueue.add(new Node(i3,j3,path,caculateDistance(i3,j3)));active[i3][j3] = true;}// 右int i4 = node.getI();int j4 = node.getJ()+1;if(isAble(i4,j4,active)){ArrayList<int[]> path = new ArrayList<>(node.getPath());path.add(new int[]{i4,j4});priorityBlockingQueue.add(new Node(i4,j4,path,caculateDistance(i4,j4)));active[i4][j4] = true;}}}// 判断坐标是否可行private boolean isAble(int i,int j,boolean[][] active){if(i<0 || i>=map.length){return false;}if(j<0 || j>= map[0].length){return false;}if(map[i][j]==1 || active[i][j]){return false;}return true;}// 计算距离终点的曼哈顿private int caculateDistance(int i,int j){return Math.abs(i-endI)+Math.abs(j-endJ);}@Data@NoArgsConstructor@AllArgsConstructorclass Node implements Comparable<Node>{int i;int j;List<int[]> path;// 距离终点的曼哈顿距离int lenToEnd;@Overridepublic int compareTo(Node o) {return Integer.compare(lenToEnd+path.size(),o.lenToEnd+o.path.size());}@Overridepublic String toString() {return "Node{" +"i=" + i +", j=" + j +", lenToEnd=" + lenToEnd +'}';}}
}
四、测试
public class Test {public static void main(String[] args) {long start = System.currentTimeMillis();int[][] map = new int[][]{{1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0},{0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0},{0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0},{0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0},{0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0},{0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1},{0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1},{0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1},{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 0, 0, 0, 0, 0},};new AStar(map).solve();System.out.println("用时:"+(System.currentTimeMillis()-start)+"ms");}
}
控制台输出:
[1, 4]
[1, 5]
[1, 6]
[1, 7]
[1, 8]
[1, 9]
[2, 9]
[2, 10]
[2, 11]
[3, 11]
[4, 11]
[5, 11]
[6, 11]
[7, 11]
[8, 11]
[9, 11]
[10, 11]
[10, 12]
[11, 12]
[12, 12]
[12, 11]
[13, 11]
[14, 11]
[15, 11]
[16, 11]
[17, 11]
[17, 12]
[17, 13]
[17, 14]
[18, 14]
[19, 14]
[19, 13]
[19, 12]
最短路长度为:33
用时:6ms
上面输出的例如:
[1, 4]
[1, 5]
[1, 6]
的文字代表最短路径(从上往下看):
即从(1,4)点走到(1,5)点,再从(1,5)点走到(1,6)点
相关文章:

【运筹优化】最短路算法之A星算法 + Java代码实现
文章目录 一、A星算法简介二、A星算法思想三、A星算法 java代码四、测试 一、A星算法简介 A*算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。 二、A星算…...
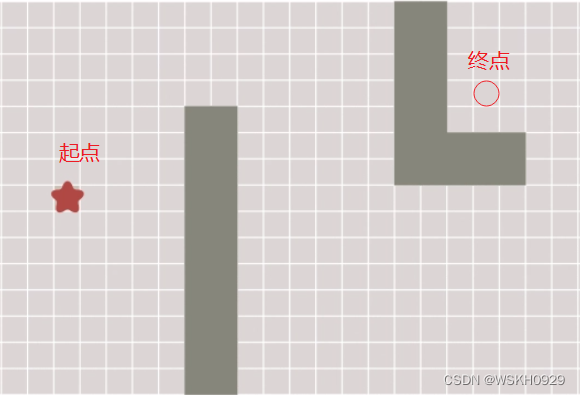
[6]PCB设计实验|认识常用元器件|电阻器|18:30~19:00
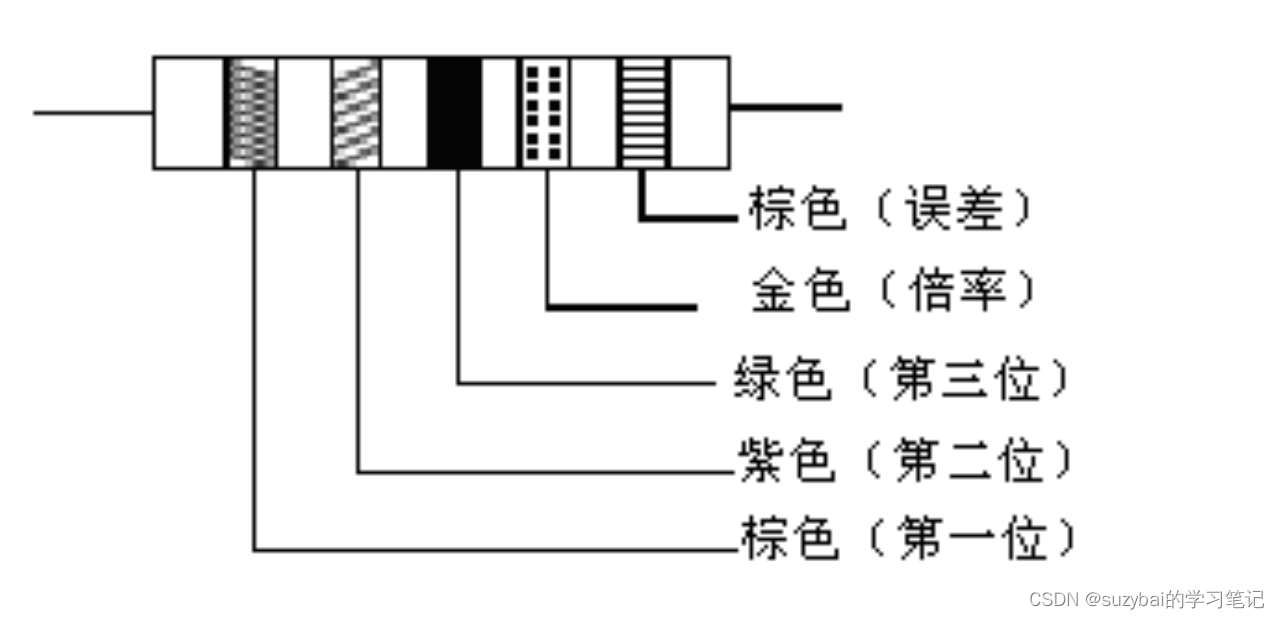
目录 一、电阻器主要用途 1. 稳定和调节电路中的电流和电压 2. 作为分流、分压和负载使用 二、常见电阻器 1. 贴片电阻 2. 热敏电阻 3. 限流电阻 4. 可调电阻 5. 排阻(网络电阻) 三、几种常用电阻器的结构特点 四、电阻的参数 1. 额定功率 电阻器功率的表示 2…...
Webots R2021a教程
文章目录 Windows安装设置中文打开世界添加贴图 为外部控制器配置Anaconda解决报错:CondaSSLError: Encountered an SSL error. Most likely a certificate verification issue.调用Python API Windows 安装 进入下载页面 https://github.com/cyberbotics/webots/r…...

C++ 输出格式控制
C 输出格式控制 需包含头文件: 浮点数精度、域宽、填充 操作符功能right-alignedright-alignedsetprecision(int n)设置以n表示的数值精度setw(int n)设置以n表示的域宽setfill(char c)设置以c表示的填充字符 输出格式 操作符功能oct以八进制格式输出数据dec以…...

【C++】引用和右值引用
目录 1. 引用 1.1 引用的概念 1.2 引用的特性 1.3 引用的使用场景 1.3.1 作为参数 1.3.2 作为返回值 1.4 常量引用 1.5 引用和指针的区别 2. 左值和右值 3. 右值引用 3.1 右值引用的概念 3.2 左值持久;右值短暂 3.3 变量是左值 3.4 标准库move函数 1.…...

NodeJS MongoDB⑦
文章目录 ✨文章有误请指正,如果觉得对你有用,请点三连一波,蟹蟹支持😘前言Node&MongoDB 第一步 连接数据库 第二步 创建User Mongodb模型 第三步 简单使用 Mongodb命令 第四步 规范使用 Mongodb命令 (…...
-共现语义篇)
情感分析实战(中文)-共现语义篇
情感分析实战(中文)-共现语义网络分析 背景:该专栏的目的是将自己做了N个情感分析的毕业设计的一个总结版,不仅自己可以在这次总结中,把自己过往的一些经验进行归纳,梳理,巩固自己的知识从而进一步提升,而帮助各大广大学子们,在碰到情感分析的毕业设计时,提供一个好的…...

【数据结构与算法】03 队列(顺序队列--循环队列--优先级队列--链队列)
一、概念1.1 队列的基本概念1.2 队列的顺序存储结构1.21 顺序队列(静态队列)1.22 循环队列1.23 优先级队列 1.3 队列的链式存储结构 二、C语言实现2.1 顺序存储2.11 顺序队列2.12 循环队列2.13 优先级队列 2.2 链式存储 一、概念 1.1 队列的基本概念 队…...

【区块链 | L2】作为Layer2赛道的领跑者,如何理解 Arbitrum?
上周我们介绍了以太坊L2扩展解决方案Optimism,本周我们继续介绍另一个L2解决方案——Arbitrum。Arbitrum 是以太坊的一个 Optimistic Rollup L2 可扩展性解决方案。 Part.1 什么是Arbitrum? Arbitrum 是一个构建在以太坊之上的区块链网络。你可以使用 Arbitrum 链来做任何在…...
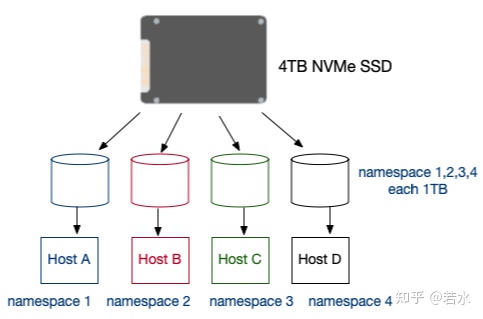
【协议】NVMe over RoCE |nvmeof
什么是nvme nvme ssd和普通ssd区别 ssd是固态硬盘,普通的ssd配的是SATA口(AHCI协议),nvme ssd配的是PCIe口(nvme传输协议) 相比普通SSD的SATA口,nvme的PCIe口有巨大的性能优势。 更多详情见&…...
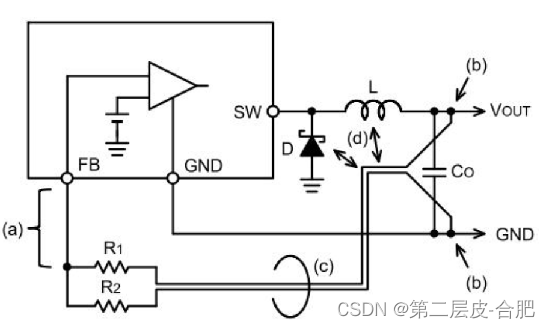
硬件设计电源系列文章-DCDC转换器布局设计
文章目录 概要 整体架构流程 技术名词解释 1.开关电源PCB布局要点 2.输入电容的放置 3.二极管的放置 4.散热孔的放置 5.反馈路径的走线 小结 概要 提示:这里可以添加技术概要 例如: 本文主要DCDC转换器布局方面的知识。 整体架构流程 提示…...

「从入门到精通,一位设计师分享学习Illustrator的技巧和经验!」
学习Illustrator的个人笔记:从入门到精通 Adobe Illustrator是一款广泛使用的矢量图形软件,用于创建各种设计作品,如商标、海报、名片等。在本篇博客中,我将分享学习Illustrator的经验和技巧,帮助您更好地掌握这一工具…...

RedisGraph的整体架构
The architecture of RedisGraph 本文关注RedisGraph的整体架构,分别从图存储模型、索引、并发控制、和执行计划四个方面简要阐述。下图为RedisGraph的整体架构图。 1 图存储模型 了解一个图数据库的架构,最重要的就是其图存储模型,即其中的…...

C#可视化 家用轿车信息查询系统(具体做法及全部代码)
目录 题目: 效果图: 数据库: 做法: combobox值更新 查询按钮功能(非空验证,查询数据) datagirdview设置 全部代码: DBHelper类 From1主窗体代码 题目: 效果图&#…...

Nautilus Chain全球行分享会,上海站圆满举办
在北京时间 6 月 9 日,由 Nautilus Chain 主办的“Layer3 模块化区块链的发展探讨”为主题的全球行活动,在上海顺利举办,本次分享会联合主办方还包 括 Stanford Blockchain Accelerator、Zebec Protocol、Tiger VC DAO、Crypto PHD、Rootz La…...

day50_mybatis
今日内容 0 复习昨日 一、分页插件 二、ORM映射【重点】 三、多表联查 【重点】 四、动态SQL 【重点】 五、$和# 零、复习昨日 mybatis orm框架,作用于持久层,高效开发,只关注sql,其他不用关心 思考MyBatis到底帮你省了哪些事情? jdbc第四步sql自己编写之外,其他mybatis都做了…...

第十一届“创业江苏”科技创业大赛正式启动
为深入实施创新驱动战略, 推进高水平科技自立自强,强化企业创新主体地位,加速推动创新要素向企业集聚,促进科技和金融深度融合,优化科技创新创业生态,吸引优秀创业团队及企业到苏州创新发展,根据…...

EasyX实现简易贪吃蛇
📝个人主页:认真写博客的夏目浅石. 📣系列专栏:夏目的C语言宝藏 文章目录 前言一、头文件包含二、创建蛇与食物的结构体三、游戏的初始化四、游戏的绘画事件五、蛇的移动事件六、输入方向七、生成食物八、吃食物九、游戏失败的判定…...

Linux下ElasticSearch7.9.2安装配置(包含服务器配置、启动停止脚本、开放端口和elasticsearch-head插件的使用)
Linux下ElasticSearch7.9.2安装配置 前言1.下载安装1.1 使用wget的方式下载1.2 官网下载 2.上传到服务器并解压3.修改es配置文件3.1 es目录简介3.2 修改配置文件 4. 创建用户并赋权5. 服务器修改配置5.1 修改文件句柄数和线程数5.2 关闭swapping5.3 修改虚拟内存 6. 启动es6.1 …...

JS 之 事件Event对象详解(属性、方法、自定义事件)
一、Event对象 1、简介 事件event对象是指在浏览器中触发事件时,浏览器会自动创建一个event对象,其中存储了本次事件相关的信息,包括事件类型、事件目标、触发元素等等。浏览器创建完event对象之后,会自动将该对象作为参数传…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
