01 背包问题解析与代码 python 实现
01 背包问题解析与代码
问题定义
给定一堆具有不同重量 { w 1 , w 2 , ⋯ , w n } \{ w_1,w_2, \cdots,w_n \} {w1,w2,⋯,wn}与价值 { v 1 , v 2 , ⋯ , v n } \{ v_1,v_2, \cdots,v_n \} {v1,v2,⋯,vn}的背包(knapsack),在总重量为 W 的情况下,如何选取背包才能获得最大价值?其中每种背包只能有被选取和不被选取两种选择。
思路解析
考虑解数组 d p [ i ] [ j ] dp[i][j] dp[i][j] ,其中的 i i i 表示尝试放入标号为 1 到 i 的背包, j j j 表示当前的限重为 j j j,数组中的值表示当前情况下可以取得的最大价值。
显然这个 dp 数组的第一行和第一列元素全为 0,逐个计算时我们使用从左到右,从上到下的原则进行计算,在计算 d p [ i ] [ j ] dp[i][j] dp[i][j] 时,需要考虑两种情况:
第一种当前的总限重是不允许放入标号为 i 的背包的,也就是当前总限重小于标号为 i 的背包的重量,那么此时的最大价值应该等于总限重为 j,且尝试放入标号为 1-(i-1) 背包时的总价值,用公式表达:
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] ( j < w [ i ] ) dp[i][j]=dp[i-1][j](j<w[i]) dp[i][j]=dp[i−1][j](j<w[i])
第二种则是当前的总限重是允许放入标号为 i 的背包的,也就是当前总限重大于标号为 i 的背包的重量,那么此时的最大价值又需要考虑两种情况,原因是放入标号为 i 的背包可能并不能取得最大价值。
放入标号为 i 的背包会产生多大的价值呢?这时我们就可以利用到先前已经计算好的解数组了,在放入标号为 i 的元素之后,背包限重变为 j - w[i],那么放入 i-1(不包含第i个) 个背包,总限重为 j - w[i] 的情况下的最大价值就是 d p [ i − 1 ] [ j − w [ i ] ] dp[i-1][j-w[i]] dp[i−1][j−w[i]],这时再加上标号 i 的背包总价值就是 d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] dp[i-1][j-w[i]]+v[i] dp[i−1][j−w[i]]+v[i]
不放入标号为i的背包的价值则为 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]
所以,此时的最大价值应当比较上述两种情况,选取最大值
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] ) ( j ≥ w [ i ] ) dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])(j \geq w[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])(j≥w[i])
这里提供一个在线练习 01背包数组填充的网站。
代码实现
def algo(weight, value, total):row = len(weight)col = total + 1res = [[0] * col for _ in range(row)]for i in range(1, row):for j in range(1, col):if weight[i] > j:res[i][j] = res[i-1][j]else:res[i][j] = max(res[i-1][j], res[i-1][j-weight[i]] + value[i])return resweight = [0, 4, 2, 3, 1]
value = [0, 9, 10, 4, 1]
total = 6print(algo(weight, value, total))
相关文章:

01 背包问题解析与代码 python 实现
01 背包问题解析与代码 问题定义 给定一堆具有不同重量 { w 1 , w 2 , ⋯ , w n } \{ w_1,w_2, \cdots,w_n \} {w1,w2,⋯,wn}与价值 { v 1 , v 2 , ⋯ , v n } \{ v_1,v_2, \cdots,v_n \} {v1,v2,⋯,vn}的背包(knapsack),在总重…...

Vue实现前端视频展示列表及特征提取、笔记、删除、文件夹组织功能
Vue实现前端视频展示列表及特征提取、笔记、删除、文件夹组织功能 在前端展示上传的视频列表时,我们可以使用Element-UI中的Card组件来实现。同时,我们还可以添加一些功能,如缓存播放的视频、选择视频文本特征提取处理、写笔记、删除视频、组…...
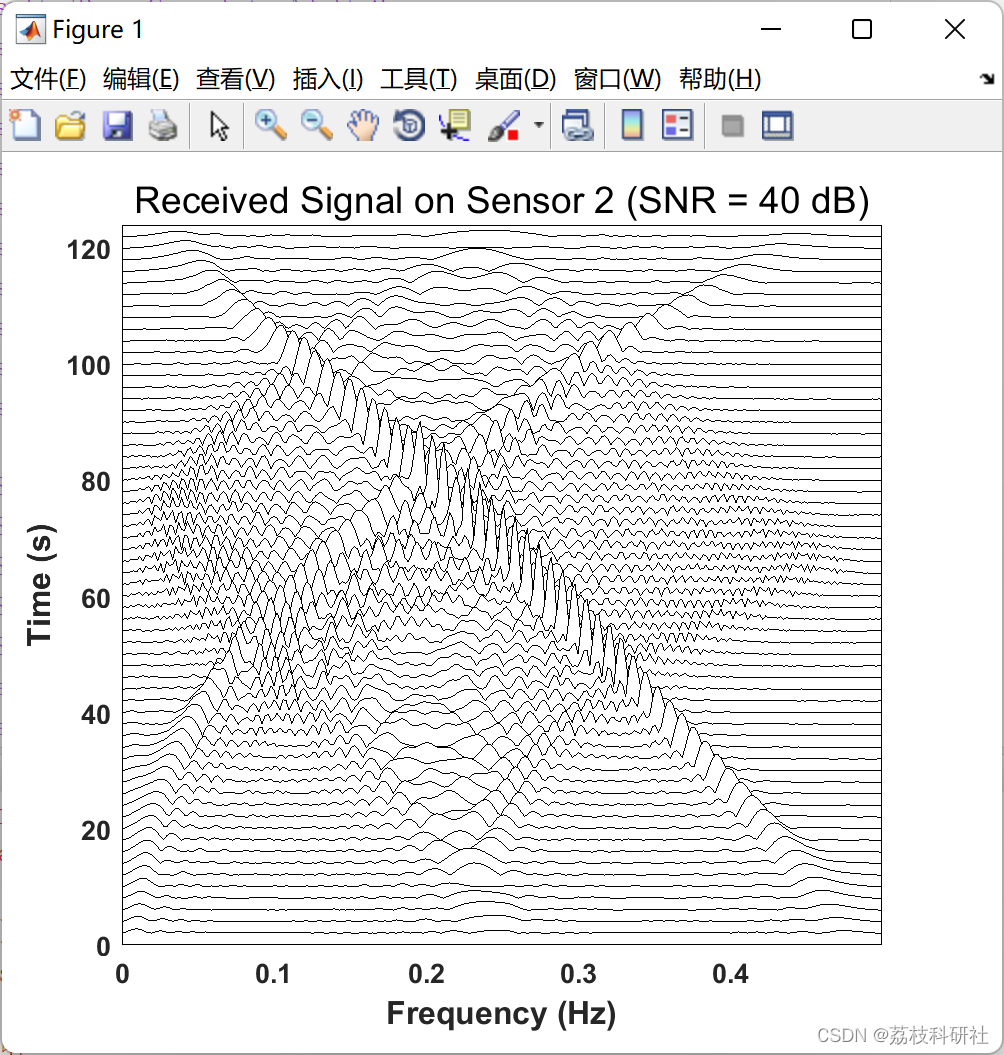
多传感器时频信号处理:多通道非平稳数据的分析工具(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

数据结构算法 -分而治之算法
引言 坤坤是一个养鸡场的员工,他非常热爱他的工作,并且总是努力提高他的专业技能。有一天,养鸡场接到了一项任务:在短时间内处理一批大量的鸡。 这批鸡数量非常大,比普通的数量要多得多,坤坤意识到他们需…...

涉密信息系统口令管理制度
第一条 口令是涉密信息系统身份认证的基本防护措施,为保障 涉密信息系统的安全运行,规范网络用户及系统口令,特制定本制度。 第二条 具有口令功能的计算机、网络设备等计算机信息系统设 备,必须使用口令对用户的身份进行验证…...

UML与流程图
UML简介 UML(Unified Modeling Language,统一建模语言)是一种用于软件系统分析与设计的标准化建模语言。它提供了一套丰富的图形符号和规则,可用于描述系统的结构、行为和交互,帮助开发人员、设计师和利益相关者之间进…...

音视频开发Level0: 入门级20~25k的工作
今天给大家分享一个音视频开发领域,入门级别的工作,要求不高。 主要做什么呢,行车记录仪,运动相机,各种拍摄器材包括医疗领域的喉镜啊,等等。 这种产品,招人的公司深圳最多,因为深…...

Git第一章、Git的原理与使用
目录 一、Git安装 1.1Linux Centos安装 二、Git基本操作 2.1创建 Git 本地仓库 2.2配置Git 三、认识工作区、暂存区、版本库 3.1添加文件(场景一) 3.2修改文件 3.3版本回退 四、撤销修改 4.1情况一:对于工作区的代码,还…...
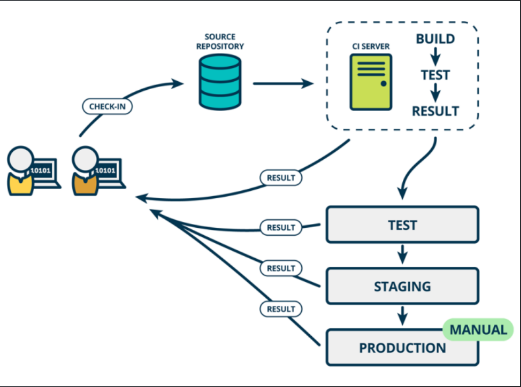
软件开发流程
目录 软件软件开发流程的演变 瀑布模型敏捷模型 XPSCRUMDevOps 1.软件 与计算机系统操作有关的计算机程序、可能有的文件、文档及数据。 软件可以分为两种主要类型: 独立软件:独立软件是一种完整的应用程序,可以直接在计算机或移动设备上…...

编程语言的优劣评选标准与未来发展趋势——探索最佳编程语言选择
编程语言的优劣评选标准与未来发展趋势——探索最佳编程语言选择 评判标准不同编程语言的优点与缺点分析对编程语言未来发展的猜测和未来趋势 💕 💕 💕 博主个人主页: 汴京城下君–野生程序员💕 💕 &#x…...

axios 发送请求请求头信息不包含Cookie信息
问题 axios 发送请求请求头信息不包含Cookie信息 详细问题 使用VueSpringBoot进行项目开发,axios进行网络请求,发送请求,请求头信息不包含Cookie信息 具体如下 实际效果 预期效果 解决方案 作用域 Vue项目全局配置 打开Vue项目的入口…...

正则表达式笔记
/你的正则表达式写在这里/ 1? 1出现0次或1次 1* 1出现0次或多次 1 1出现1次或多次 1{2} 1出现了2次 1{2,3} 1出现了2到3次 1{2,} 1出现了2次及以上 (5555){1} 5555出现了1次 (dog|cat) dog或者cat [a-zA-Z] a…...
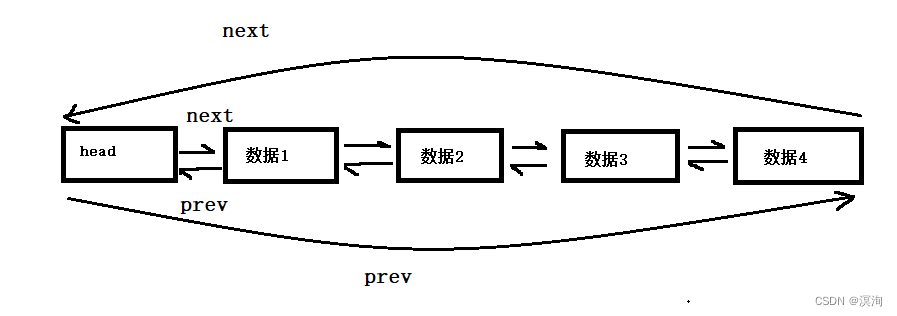
数据结构链表(C语言实现)
绪论 机遇对于有准备的头脑有特别的亲和力。本章将讲写到链表其中主要将写到单链表和带头双向循环链表的如何实现。 话不多说安全带系好,发车啦(建议电脑观看)。 附:红色,部分为重点部分;蓝颜色为需要记忆的…...

Springboot实现接口传输加解密
前言 先给大家看下效果,原本我们的请求是这样子的 加密后的数据传输是这样子的 加解密步骤: 1.前端请求前进行加密,然后发送到后端 2.后端收到请求后解密 3.后端返回数据前进行加密 4.前端拿到加密串后,解密数据 加解密算法&…...

TypeScript类型系统:强类型的优势和使用方式
目录 引言强类型的优势更好的代码可读性更好的代码可维护性更好的代码重构能力更好的代码可靠性更好的代码重用能力 使用方式声明变量类型函数参数和返回值类型类型别名泛型类型(了解) 总结 引言 在上一篇文章《TypeScript入门指南:从JS到TS的…...

有没有可以代替风铃系统的专业问卷工具?
风铃系统问卷是一种流行的调查和数据分析工具,已广泛应用于学术研究、市场营销和社会科学。然而,有几种替代产品提供了与风铃系统类似的特性和功能,可以被企业用来进行调查和分析数据。在这篇文章中,我们将介绍风铃系统的十大替代…...

【数字调制】数字调制技术FSK与PSK分析与研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

html实现好看的个人介绍,个人主页模板4(附源码)
文章目录 1.设计来源1.1 主界面1.2 我的文章界面1.3 我的相册界面1.4 关于我界面1.5 联系我界面 2.效果和源码2.1 动态效果2.2 源代码2.2 源代码目录 源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/details/131265259 …...
内存不够用,那你的内存去哪了?
一、前言 近几年开发了一些大型的应用程序,在程序性能调优或者解决一些疑难杂症问题的过程中,遇到最多的还是与内存相关的一些问题。例如glibc内存分配器ptmalloc,google的内存分配器tcmalloc都存在“内存泄漏”,即内存不归还操作…...
)
哈希表--day4--(leetcode202/leetcode1/leetcode454)
文章目录 leetcode202. 快乐数基本思路AC-code leetcode1. 两数之和基本思路AC-code 454.四数相加II基本思路AC-code leetcode202. 快乐数 链接 基本思路 实际上题目隐藏着一个小细节,就是告诉你会发生无限循环,那我们该如何跳出这个无限循环就是一个…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
