Leetcode---350周赛
题目列表
6901. 总行驶距离
6890. 找出分区值
6893. 特别的排列
6447. 给墙壁刷油漆
一、总行驶距离

很显然,这题单纯就是一道数学应用题,我们要明白最关键的一点 :只有当mainTank>=5并且additionalTank>0时,才能发生副油箱的油转移到主油箱,代码如下
int distanceTraveled(int mainTank, int additionalTank){int ans=0;while(mainTank/5){//这一条件等价于mainTank>=5ans+=50;mainTank-=5;if(additionalTank>=1){mainTank++;additionalTank--;}}ans+=mainTank*10;//记得加上主油箱中剩余的油所能跑的路程return ans;
}二、找到分区值
这题其实题目看懂就不算很难,就是让你将nums数组拆成俩个数组,找到第一个数组的max,第二个数组的min,返回max和min的最小差值,乍一看,这题好像需要枚举所有可能的拆分方法,但仔细看一下元素的个数范围,你就会知道这不现实,那么我们该怎么做?
首先,我们可以明确的是:我们可以通过分配数组元素,将任何一个数通过最大值或最小值拿出来,那么我们可不可以通过分配数组元素将任意两个数通过最大值和最小值的形式拿出来?
假设能这样操作,那么该问题就会变成找到两个数的差值最小的问题,而后面一个问题解决起来就会很容易,那么到底能不能这么操作呢?
我们假设原始数组中的两个数为x,y(x<=y),分成的两个数组分别是数组A和数组B,我们将x和大于y的数全部放到数组A,将剩余的数全部放入数组B,那么数组A的最小值就是x,数组B的最大值就是y,很显然我们能够选取出任意x,y
代码如下
int cmp(int*p1,int*p2){return *p1-*p2;
}
int findValueOfPartition(int* nums, int numsSize){qsort(nums,numsSize,sizeof(int),cmp);int ans=INT_MAX;for(int i=1;i<numsSize;i++){if(nums[i]-nums[i-1]<ans){ans=nums[i]-nums[i-1];}}return ans;
}三、特别的排列

这题的思路其实不是很难,只要会回溯就能做出来,但是会超时,得用记忆化搜索,减少时间复杂度,或者直接用递推。
讲一下这类回溯的基本思路:首先要有数组记录数字有没有被使用过,因为需要考虑数字所在的位置问题,然后不断dfs找到适合当前位置的数字,直到将所有的数字都选上,记入答案 ,最后返回
这里的思路说的比较简单,具体的可以看该题的代码的逻辑
//注意:这是正常的回溯代码--->会超时
const int MOD=1e9+7;//题目要求答案取模,为了防止数字超出int的范围,我们将所有计算结果都取模
int* visited;//记录数字是否被使用
int dfs(int i,int depth,int n,int* nums){//i是前一个数的下标,depth记录用了几个数,n代表数的个数,nums数组if(depth==n){return 1;//返回1,代表找到一种组合方法}int res=0;for(int j=0;j<n;j++){if(!visited[j]&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited[j]=1;res=(res+dfs(j,depth+1,n,nums))%MOD;visited[j]=0;}}return res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(int*)malloc(sizeof(int)*n);memset(visited,0,sizeof(int)*n);for(int i=0;i<n;i++){visited[i]=1;ans=(ans+dfs(i,1,n,nums))%MOD;visited[i]=0;}free(visited);return ans;
}好,写到这一步,我们会发现超时,这里超时的原因和求较大值的斐波那契数列一样,相同的递归进行太多次,我们需要用数组记录我们已经计算过的dfs,这样之后我们在需要时,就不用计算直接返回,从而减少时间复杂度
而这题的难点在于:我们需要进行状态压缩之后才能进行记忆化搜索,而状态压缩在本题中就是将visited数组用二进制的数来表示
举个栗子:
状态压缩后的代码如下:
//依旧会超时,但空间复杂度降低
const int MOD=1e9+7;
int visited;
int dfs(int i,int n,int* nums){if(visited==0){//visited==0,代表所有的数都被使用return 1;}int res=0;for(int j=0;j<n;j++){if((visited&(1<<j))&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited^=(1<<j);res=(res+dfs(j,n,nums))%MOD;visited^=(1<<j);}}return res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(1<<n)-1;for(int i=0;i<n;i++){visited^=(1<<i);ans=(ans+dfs(i,n,nums))%MOD;visited^=(1<<i);}return ans;
}下面我们只要有一个数组来储存已经计算过的dfs,从而实现记忆化搜索就行,但这个数组的形状(一维,二维...)大小是什么呢?
这里我们只要看dfs函数是由几个关键的参数决定的就行(因为dfs其实就是在求某种状态,我们要建立数组储存状态,肯定是看共多少种状态来决定数组的形状大小,而状态是由参数决定的,所以我们看参数),很显然nums是辅助型参数,不对dfs的状态产生影响,其他的都有影响,即两个参数=>二维数组,这两个参数的范围=>数组的大小
记忆化搜索的代码如下:
const int MOD=1e9+7;
int visited;
int**memo;
int dfs(int i,int n,int* nums){if(visited==0){return 1;}if(memo[i][visited]!=-1)return memo[i][visited];int res=0;for(int j=0;j<n;j++){if((visited&(1<<j))&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited^=(1<<j);res=(res+dfs(j,n,nums))%MOD;visited^=(1<<j);}}return memo[i][visited]=res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(1<<n)-1;memo=(int**)malloc(sizeof(int*)*n);for(int i=0;i<n;i++){int s=1<<n;memo[i]=(int*)malloc(sizeof(int)*s);for(int j=0;j<s;j++){memo[i][j]=-1;}}for(int i=0;i<n;i++){visited^=(1<<i);ans=(ans+dfs(i,n,nums))%MOD;visited^=(1<<i);}for(int i=0;i<n;i++){free(memo[i]);}free(memo);return ans;
}其实,这题还有一种写法,就是递推,我们可以直接将上面的记忆化搜索直接转换成递推
const int MOD=1e9+7;
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;int visited=(1<<n)-1;int s=1<<n;int f[n][s];memset(f,0,sizeof(f));for(int i=0;i<n;i++){f[i][0]=1;}//首先枚举状态,注意这里先枚举列,再枚举行,因为每一列的状态由它的上一列状态推出for(int i=1;i<s;i++){for(int j=0;j<n;j++){//然后计算每一个状态long long res=0;for(int k=0;k<n;k++){if((i&(1<<k))&&(nums[j]%nums[k]==0)||(nums[k]%nums[j]==0)){res=(res+f[k][i^(1<<k)])%MOD;}}f[j][i]=res;}}for(int i=0;i<n;i++)ans=(ans+f[i][visited^(1<<i)])%MOD;return ans;
}四、给墙壁刷油漆
这题其实和上一题很相似,思路:一面墙要么是免费刷的消耗时间,要么是付费刷的增加时间和金额,取较小值,即dfs(i,j) = min { dfs(i - 1 ,j - 1) ,dfs( i - 1,j + time[ i ] ) + cost[ i ] }
递归边界:1. j>=i+1,即剩下的墙可以免费刷,返回0
2. i<0并且j<i+1,即没有墙可刷,但是还欠费,该方案不符合条件,返回一个正无穷(就是一个无法作为答案的正数,目的是在取较小值时,不影响答案取值)
递归入口:一开始,从最后一面墙开始(下标是n-1),时间为0,dfs(n-1,0)
代码如下:
//正常的递归:超时
long long dfs(int i,int j,int* cost,int* time)//剩余第0~i面墙,剩余花费的时间j,返回所需要的金额
{if(j>i)return 0;//等价j>=i+1,这里的i是用下标表示的墙的个数if(i<0)return INT_MAX;//i<0&&j<=i,即欠费时间return fmin(dfs(i-1,j-1,cost,time),dfs(i-1,j+time[i],cost,time)+cost[i]);
}
int paintWalls(int* cost, int costSize, int* time, int timeSize){int n=costSize;return dfs(n-1,0,cost,time);
}//记忆化搜索--可以过
//dfs(i,j)=fmin(dfs(i-1,j),dfs(i-1,j-time[i])+cost[i])
#define MIN(x,y) ((x)>(y)?(y):(x))//这是宏定义,或者你定义函数都行,用来比较大小
//以下全局变量是为了减少函数参数个数,使dfs函数的逻辑更加清晰,当然把它们放入参数中也是可以的
int*Cost;
int*Time;
int**memo;
int N;
int dfs(int i,int j){if(j>=i+1)return 0;//如果免费的时间>=要刷的墙的数量,那么剩下的墙直接免费if(i<0)return INT_MAX/2;//如果墙全刷完后,j<i+1=0,返回正无穷(该值取决于题目的可能答案区间,和函数返回值类型)if(memo[i][j+N-1]!=-1)return memo[i][j+N-1];return memo[i][j+N-1]=MIN(dfs(i-1,j-1),dfs(i-1,j+Time[i])+Cost[i]);
}
int paintWalls(int* cost, int costSize, int* time, int timeSize){int n=costSize;N=costSize;Cost=cost;Time=time;memo=(int**)malloc(sizeof(int*)*n);for(int i=0;i<n;i++){memo[i]=(int*)malloc(sizeof(int)*(2*n));for(int j=0;j<2*n;j++){memo[i][j]=-1;}}int res = dfs(n-1,0);for(int i=0;i<n;i++){free(memo[i]);}free(memo);return res;
}上面代码中的memo数组的第二维度(时间维度)的范围是[-(n-1),n],即最多连续有n-1面墙免费和n面墙的免费时间,其他的状态会被直接返回0或INT_MAX/2,而要表示负的情况我们只能将每个数加上n-1,得到[0,2n-1],而这是下标范围,我们数组大小就是2n
当然,这题其实也是一种01背包问题的变形,以后找时间出一期01背包问题的详解。
关注我,让你了解更多周赛题目!!!
不要忘记点赞,评论加收藏哦!!!!!!
相关文章:

Leetcode---350周赛
题目列表 6901. 总行驶距离 6890. 找出分区值 6893. 特别的排列 6447. 给墙壁刷油漆 一、总行驶距离 很显然,这题单纯就是一道数学应用题,我们要明白最关键的一点 :只有当mainTank>5并且additionalTank>0时,才能发生副油…...

Django通过Nginx和uWSGI实现负载均衡
Django是一款非常流行的Web应用程序框架,它允许开发人员以快速、简单和灵活的方式构建可扩展和可维护的Web应用程序。当你的应用程序开始变得越来越受欢迎时,你可能会发现需要使用负载均衡来确保应用程序的可用性和性能。在本文中,我们将介绍…...
单元测试框架——Junit5
文章目录 Junit1. 注解2.断言3.测试用例执行顺序4.测试套件Suite1) 指定多个类2) 指定包 5. 参数化1) 单参数2) 多参数3) 文件注入 6.动态参数 Junit Junit是一个开源的用于Java语言的单元测试框架,也是Java方向使用最广泛的单元测试框架。 在pom.xml中引入Junit5…...

centos 系列添加 yum 源
nginx 首先,安装 EPEL (Extra Packages for Enterprise Linux) 仓库。这是一个由 Fedora 项目提供的免费扩展软件包仓库,其中包含许多有用的软件包。 sudo yum install epel-release 接下来,导入 Nginx 的官方 GPG 密钥,以便验证安…...

[Hive高级特性与 DDL和DML语法]
目录 🎇前言: 🎇 HiveQL语言的基本语法,包括DDL和DML两个方面。 🎇DDL(数据定义语言): 🎇DML(数据操作语言): 🎇 Hive高级特性 多种…...
Web服务器群集:Web基础与HTTP协议
目录 一、理论 1.Web基础 2.HTTP协议 二、实验 1.浏览本地HTML页面 三、总结 一、理论 1.Web基础 (1)域名和DNS ① 域名 网络是基于TCP/IP 协议进行通信和连接的,每一台主机都有一个唯一的标识(固定的IP地 址࿰…...

cmd命令常用速记
cmd命令大全 常见的appwiz.cpl control calc 等,各类功能、设置、甚至是文件属性和系统版本,都可以通过命令的方式快速查看和操作,有助于我们的提高工作效率,具体见下文。 cmd命令:开始->运行->键入…...

Python网络爬虫基础进阶到实战教程
文章目录 认识网络爬虫HTML页面组成Requests模块get请求与实战效果图代码解析 Post请求与实战代码解析 发送JSON格式的POST请求使用代理服务器发送POST请求发送带文件的POST请求 Xpath解析XPath语法的规则集:XPath解析的代码案例及其详细讲解:使用XPath解…...
树莓派使用VNC、SSH、Xrdp等方式进行远程控制的方法和注意事项
下面来总结一下远程操控树莓派用到的三种方式及其注意事项,其实这三种方式对于所有的Linux系统来说都是适用的。 目录 一、ssh控制树莓派 1.开启 ssh服务方法一 2.开启 ssh服务方法二 二、VNC远程连接 三、xrdp远程连接 四、其他注意事项 一、ssh控制树莓派 S…...

C++ 第二弹封装-类和对象
目录 1.类的引入 2.类的定义方式 3.访问权限 4.封装 5.类也是作用域 6.类的实例化 7.如何求一个类的大小 8.this指针 9.默认成员函数 10.构造函数 11.析构函数 12.拷贝构造函数 13.赋值运算符重载 14.const的类成员 15初始化列表 16.static的类成员 17.友元 …...
浅析 GeoServer CVE-2023-25157 SQL注入
原创稿件征集 邮箱:eduantvsion.com QQ:3200599554 黑客与极客相关,互联网安全领域里 的热点话题 漏洞、技术相关的调查或分析 稿件通过并发布还能收获 200-800元不等的稿酬 更多详情,点我查看! 简介 GeoServer是一个开…...

1001router6-react
文章目录 1 一级路由2 Navigate3 NavLink 自定义高亮样式4 useRoutes()5 嵌套路由6 路由传参6.1 传递params参数6.2 传递search参数6.3 传递state参数 7 编程式导航7.1 路由跳转7.2 前进、后退 8 钩子函数8.1 useInRouterContext()8.2 useNavigationType()8.3 useOutlet()8.4 u…...
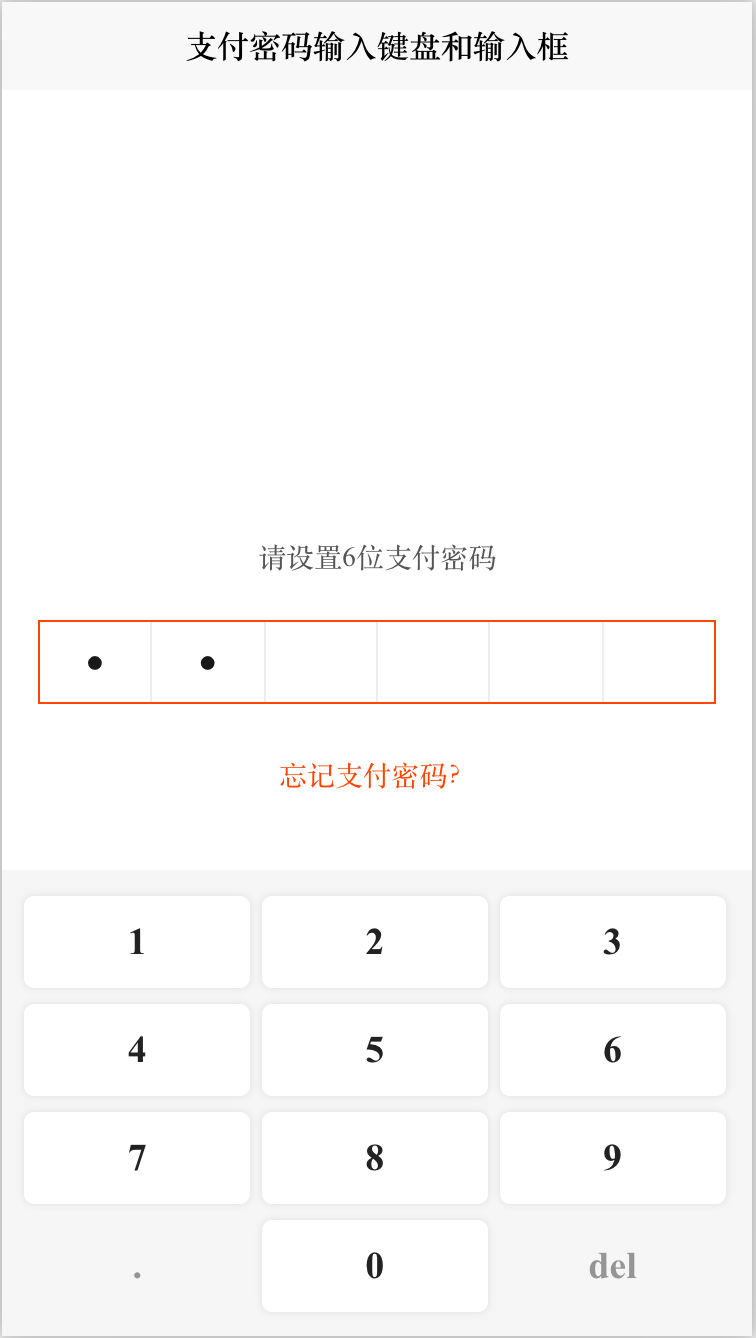
前端Vue自定义支付密码输入键盘Keyboard和支付设置输入框Input
前端Vue自定义支付密码输入键盘Keyboard和支付设置输入框Input, 下载完整代码请访问uni-app插件市场地址:https://ext.dcloud.net.cn/plugin?id13166 效果图如下: # cc-defineKeyboard #### 使用方法 使用方法 <!-- ref:唯一ref pas…...
)
VB+ACCESS超市管理系统设计(源代码+系统)
超市管理系统是典型的信息管理系统(MIS),其开发主要包括后台数据库的建立和维护以及前端应用程序的开发两个方面。对于前者要求建立起数据一致性和完整性强、数据安全性好的库。而对于后者则要求应用程序功能完备,易使用等特点。经过分析,我们使用 MICROSOFT公司的 VISUAL BASI…...

【机器学习】十大算法之一 “神经网络”
作者主页:爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?typeblog个…...

【MarkDown】CSDN Markdown之流程图graphflowchart详解
基本语法 flowchart/graph 流程图(Flowcharts/Graphs)是由节点 (几何形状) 和连接线 (箭头或线条)组成的. Mermaid代码定义了节点和连线的编码方式,并支持不同的箭头类型、多向箭头以及子图之间的任意链接。 警告 如果在流程图的节点使用e…...
Git下:Git命令使用-详细解读
目录 一、Git 安装 二、Git 配置 三、Git 工作流程 四、Git 工作区、暂存区和版本库 五、常用 Git 命令清单 1. 创建仓库 2. 增加/删除文件 3. 代码提交 4. 分支管理 5. 标签 6. 查看历史提交 7. 远程仓库同步 8. 撤销操作 六、Git 常用命令速查表 七、Git 电子…...
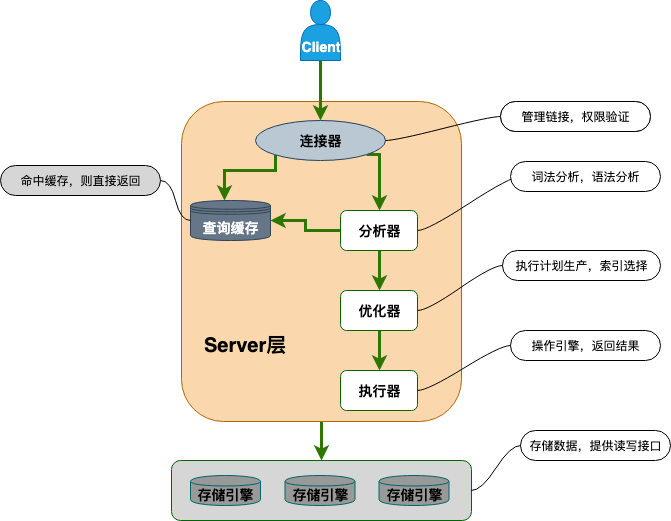
一条SQL语句的前世今生
文章目录 MySQL 基础架构分析语句分析查询语句更新语句 总结 本篇文章会分析下一个 SQL 语句在 MySQL 中的执行流程,包括 SQL 的查询在 MySQL 内部会怎么流转,SQL 语句的更新是怎么完成的。 MySQL 基础架构分析 下图是 MySQL 的一个简要架构图ÿ…...

各种架构比较
架构特点适用领域x86- 市场份额大,广泛支持和应用<br>- 成熟稳定,软件生态丰富<br>- 相对较低的功耗<br>- 适用于桌面、服务器和嵌入式系统等桌面应用、服务器、嵌入式系统x86-64- 支持 64 位操作系统和应用程序<br>- 更大的内存…...

scapy定制数据包探测主机
kali 输入scapy 进入界面 scapy定制ARP协议 输入ARP().display()显示ARP包的详细信息 输入sr1(ARP(pdst"192.168.133.2")),向网关发送arp请求数据包 scapy定制PING包 输入IP().display()显示IP包的详细信息 输入ICMP().display()显示ICMP包的详细信息…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
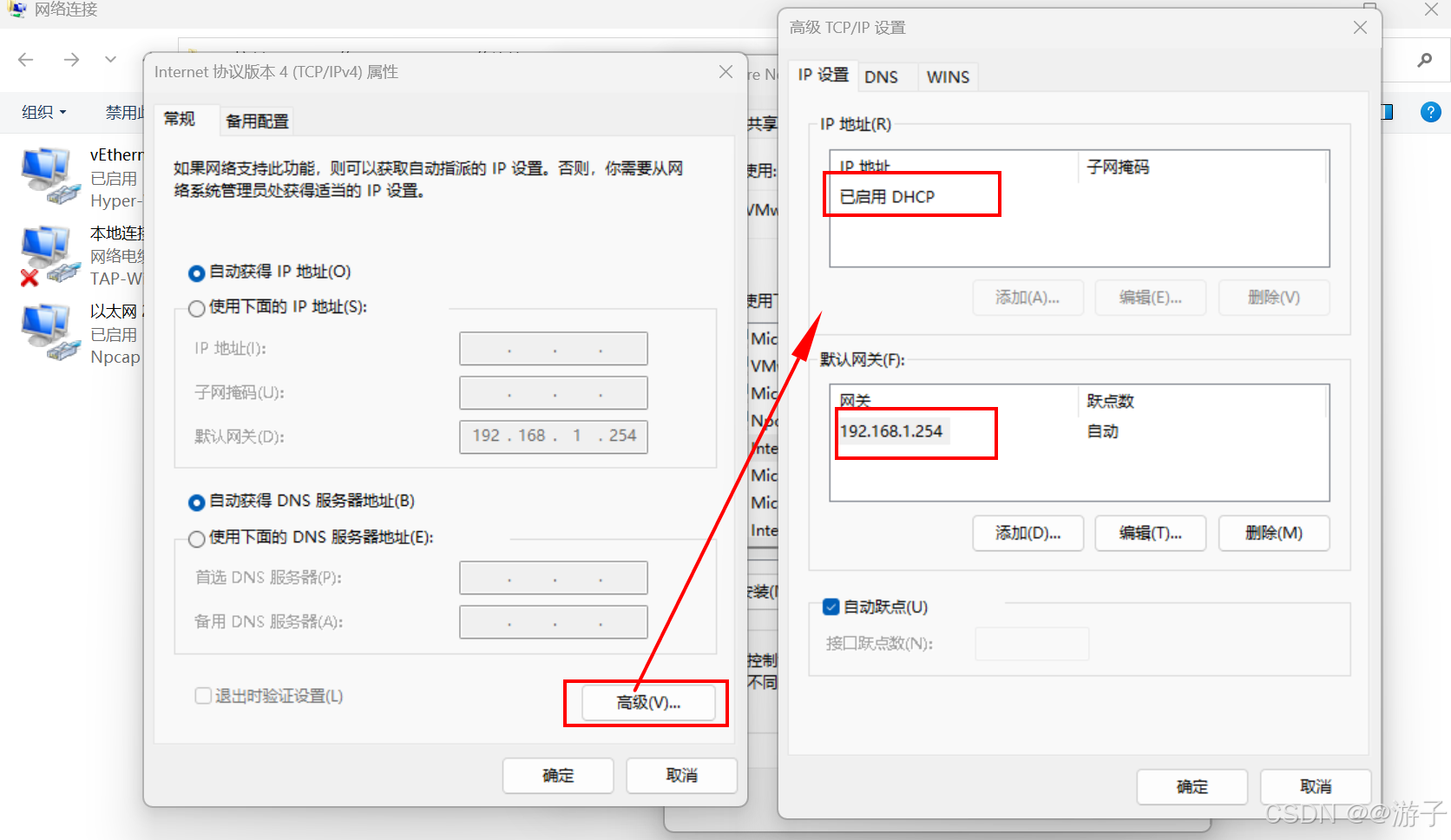
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...
