CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 思路
- 代码实现
题目
链接
https://www.luogu.com.cn/problem/CF1790E
字面描述
题面翻译
共有 ttt 组数据。
每组数据你会得到一个正整数 xxx,你需要构造一组正整数 aaa 和 bbb,满足:
-
a+b=x×2a + b = x \times 2a+b=x×2;
-
axorb=xa \operatorname{xor} b = xaxorb=x,其中 xor\operatorname{xor}xor 指异或。
输出你构造的 aaa 和 bbb。如有多解,任意输出一解即可。如无解,输出 −1-1−1。
1≤t≤1041 \leq t \leq 10^41≤t≤104,1≤x≤2291 \leq x \leq 2^{29}1≤x≤229。同时,你需要保证你构造的 aaa,bbb 满足 1≤a,b≤2301 \leq a,b \leq 2^{30}1≤a,b≤230。
题目描述
Vlad found two positive numbers $ a $ and $ b $ ( $ a,b>0 $ ). He discovered that $ a \oplus b = \frac{a + b}{2} $ , where $ \oplus $ means the bitwise exclusive OR , and division is performed without rounding…
Since it is easier to remember one number than two, Vlad remembered only $ a\oplus b $ , let’s denote this number as $ x $ . Help him find any suitable $ a $ and $ b $ or tell him that they do not exist.
输入格式
The first line of the input data contains the single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test.
Each test case is described by a single integer $ x $ ( $ 1 \le x \le 2^{29} $ ) — the number that Vlad remembered.
输出格式
Output $ t $ lines, each of which is the answer to the corresponding test case. As the answer, output $ a $ and $ b $ ( $ 0 < a,b \le 2^{32} $ ), such that $ x = a \oplus b = \frac{a + b}{2} $ . If there are several answers, output any of them. If there are no matching pairs, output -1.
样例 #1
样例输入 #1
6
2
5
10
6
18
36
样例输出 #1
3 1
-1
13 7
-1
25 11
50 22
思路
根据题目 a+b=2x和aa+b=2x和aa+b=2x和a xorxorxor b=xb=xb=x
我们能发现一个非常高重要的突破点a异或b流失了xa异或b流失了xa异或b流失了x
∴a按位与b=x/2a按位与b=x/2a按位与b=x/2
∵题目可输出任意解
∴a=x/2,b=x+x/2a=x/2,b=x+x/2a=x/2,b=x+x/2
但我们还要考虑一个无解的情况:
当x是奇数时,无法被2整除,无解
当(x/2)按位与x!=0(x/2)按位与x!=0(x/2)按位与x!=0,有误,无解
OK,过程理完,上代码
代码实现
#include<bits/stdc++.h>
using namespace std;int t,n;
int main(){scanf("%d",&t);while(t--){scanf("%d",&n);if(n%2==1){printf("-1\n");continue;}if(((n/2)&n)!=0){printf("-1\n");continue;}printf("%d %d\n",n/2,n/2+n);}return 0;
}
相关文章:

CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1790E 字面描述 题面翻译 共有 ttt 组数据。 每组数据你会得到一个正整数 xxx&…...

漏洞预警|Apache Kafka Connect JNDI注入漏洞
棱镜七彩安全预警 近日网上有关于开源项目Apache Kafka Connect JNDI注入漏洞,棱镜七彩威胁情报团队第一时间探测到,经分析研判,向全社会发起开源漏洞预警公告,提醒相关安全团队及时响应。 项目介绍 Karaf是Apache旗下的一个开…...

企业小程序开发步骤【教你创建小程序】
随着移动互联网的兴起,微信已经成为了很多企业和商家必备的平台,而其中,微信小程序是一个非常重要的工具。本文将为大家介绍小程序开发步骤,教你创建小程序。 步骤一、注册小程序账号 先准备一个小程序账号,在微信公…...

刚性电路板的特点及与柔性电路板的区别
打开市场上的任何一个电子产品,会发现里面都有一块或多块电路板。电路板是电子产品运行的核心,之前沐渥小编已经给大家介绍了柔性电路板,下面给大家介绍刚性电路板的基础知识。 刚性电路板俗称硬板,是由不容易变形的刚性基材制成的…...

扫码过磅+车牌识别,内蒙古蒙维过磅实现信息化管理
扫码过磅、车牌识别、对接SAP ERP系统设计思路: 无人值守系统升级改造包括车牌自动识别系统、信息化(扫码等方式)管理系统、智能自动控制系统等实现信息无纸化传递。远程监管地点设于公司东磅房,可以实现远程监测监控画面、称重过…...
蒙特卡洛计算圆周率
使用MC计算圆周率的小例子,使用python的numpy,matplotlib库import numpy as npimport matplotlib.pyplot as pltdef mc_calculate_pi(t):np.random.seed(t)rand_num np.random.rand(t)rand_num2 np.random.rand(t)l1 rand_num-0.5l2 rand_num2-0.5l0…...
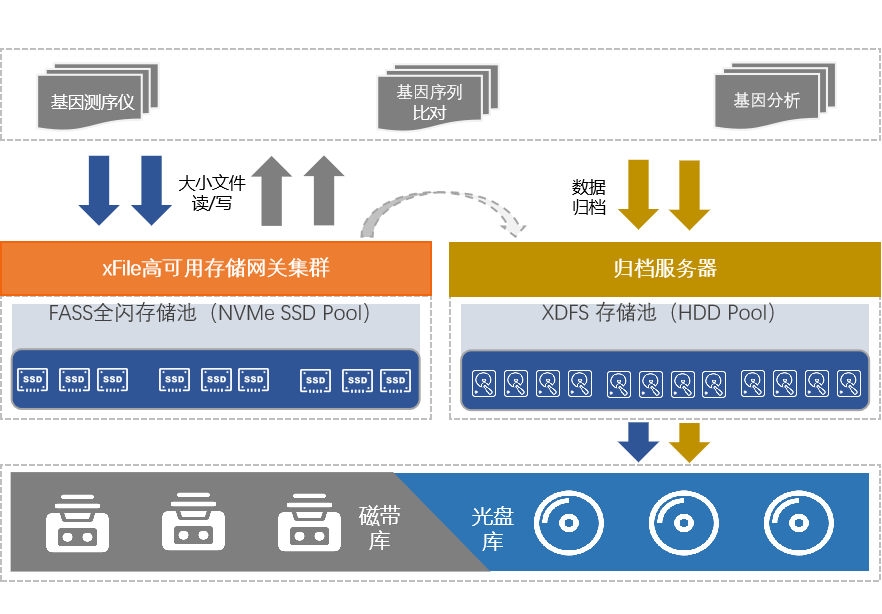
生物信息场景下的用户需求
背景分析概念定义基因测序是一种新型基因检测技术,是基因检测的方法之一,其又叫基因谱测序,是国际上公认的一种基因检测标准。基因测序技术能锁定病变基因,提前预防和治疗。过长的测序周期以及上万美元的仪器成本,成了…...
和sudo(superuser do)的区别?(sudo su与su的区别))
linux su(switch user)和sudo(superuser do)的区别?(sudo su与su的区别)
文章目录linux su(switch user)和sudo(superuser do)的区别?sudo su与su的区别linux su(switch user)和sudo(superuser do)的区别? 在Unix或Linux操作系统中…...
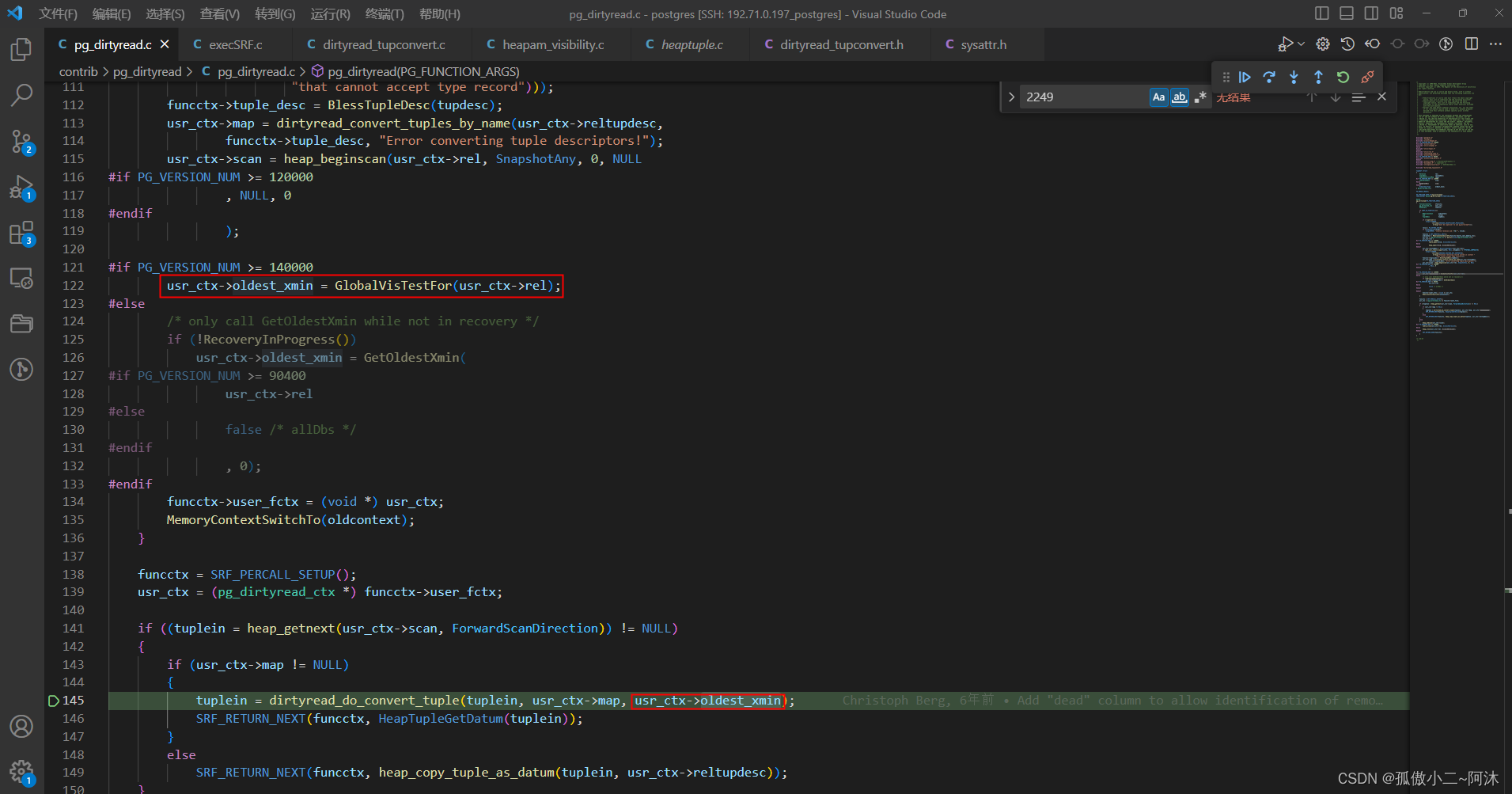
PostgreSQL的学习心得和知识总结(一百二十三)|深入理解PostgreSQL数据库开源扩展pg_dirtyread的使用场景和实现原理
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...
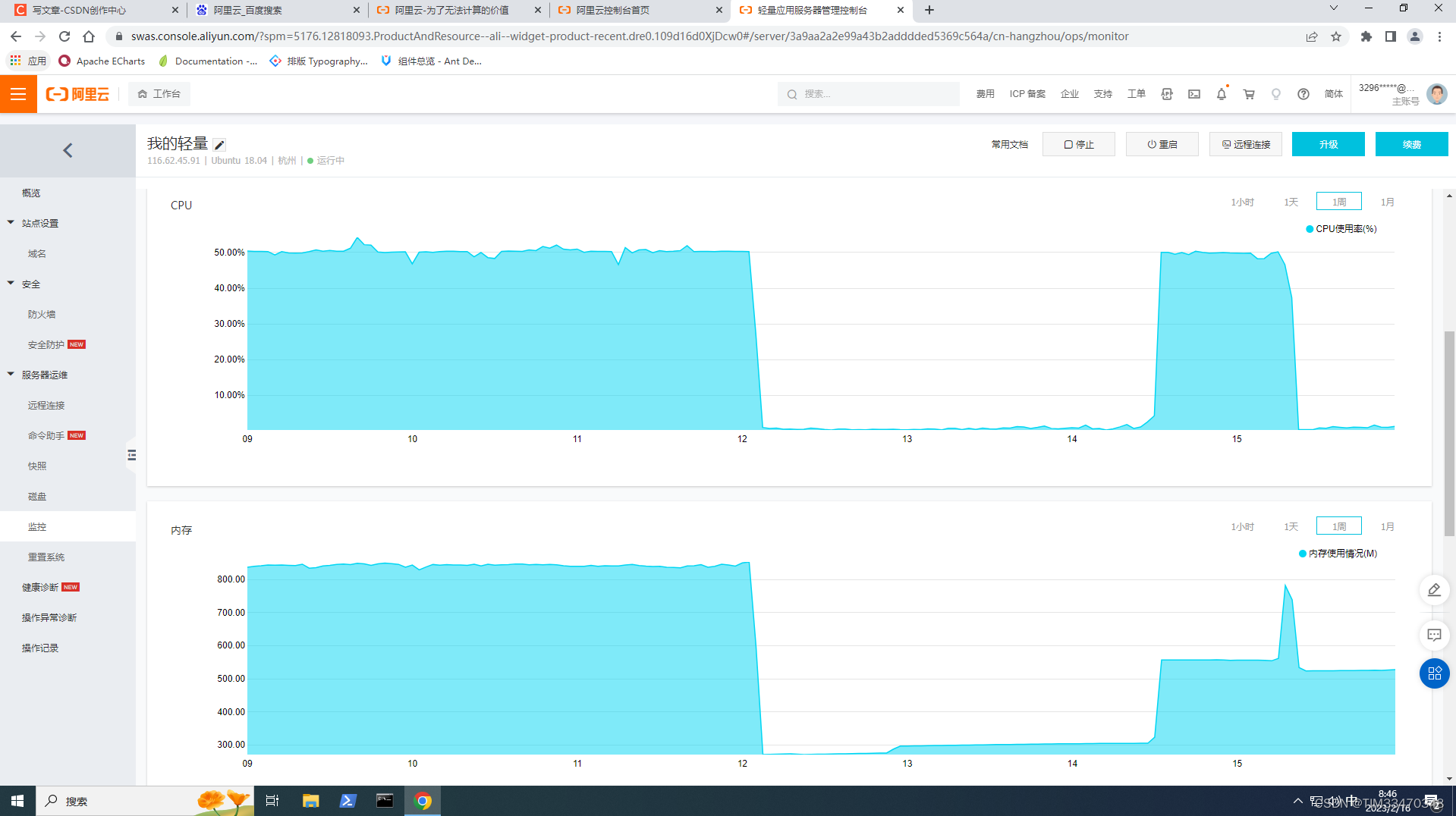
ubuntu清理挖矿病毒
0 序言 我之前搭建的hadoop用于测试,直接使用了8088和9870端口,没有放入docker,从而没有端口映射。于是,就被不法之徒盯上了,hadoop被提交了很多job,使得系统被感染了挖矿病毒,在前几天阿里云站…...

【代码随想录训练营】【Day16】第六章|二叉树|104.二叉树的最大深度|559.n叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树的最大深度 题目详细:LeetCode.104 递归法很容易理解: 定义一个全局变量max, 记录二叉树的最大深度在递归函数中增加一个深度参数,表示当前的节点的深度然后对二叉树进行深度优先遍历当遍历到叶子节点时,比较…...
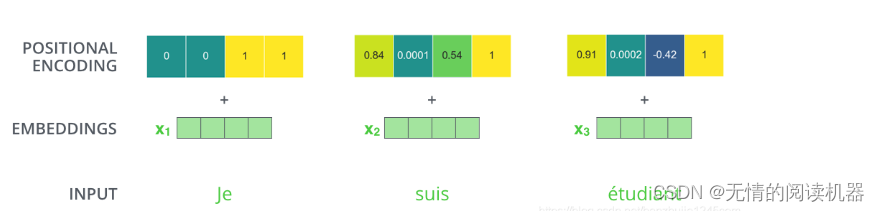
transformer总结
1.注意力机制 意义:人类的注意力机制极大提高了信息处理的效率和准确性。 公式: 1)自注意力机制 b都是在考虑了所有a的情况下生成的。 以产生b1向量为例: 1.在a这个序列中,找到与a1相关的其他向量 2.每个向量与a1关联的程度&a…...

dart flutter入门教程,开发手册 分享
我最近在学校dart flutter.这是我收集的一些手册和教程. 不需要关注公众号,不需要加好友. 我发现flutter(dart)的中文资料比较奇缺.入门的教程非常多.但是api手册几乎没有(全是英文的). 收集原则 1.中文(我英文不好) 2.不要pdf的,网上有一些pdf的 从入门到进阶的,但是太长…...

教育舆情监测关键词有哪些,TOOM教育舆情监测系统流程?
教育舆情监测是指对教育领域的舆情进行收集、分析和处理的过程。舆情是指公众在各种渠道上对教育政策、教育机构、教育事件等方面的言论、态度和情绪。通过对教育舆情的监测和分析,可以了解公众对教育行业的看法和反应,提高对教育行业的管控能力…...
MySQL高级(一)
MySQL-day01 1 MySQL简介 1.1 MySQL简介 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB(创始人Michael Widenius)公司开发,2008被Sun收购(10亿美金),2009年Sun被Oracle收购。MariaDBMaria…...
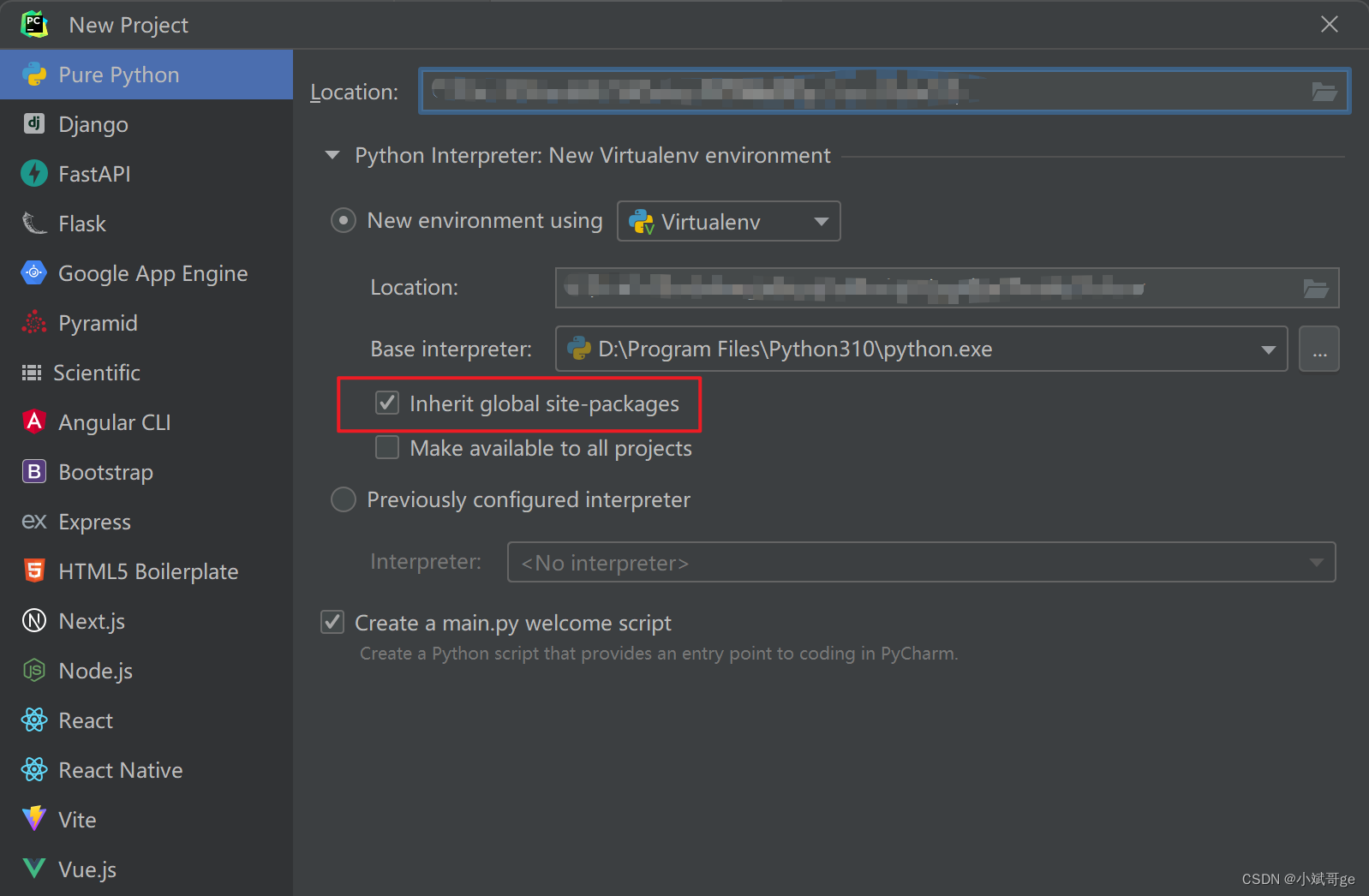
如何将Python项目部署到新电脑上运行?
如何将Python项目部署到新电脑上运行? 在工作中,可能需要在新服务器上部署项目代码,例如新增服务器、把测试环境的代码部署到生产环境等。 在生活中,也会遇到换新电脑,需要将自己在旧电脑上写的(项目&…...
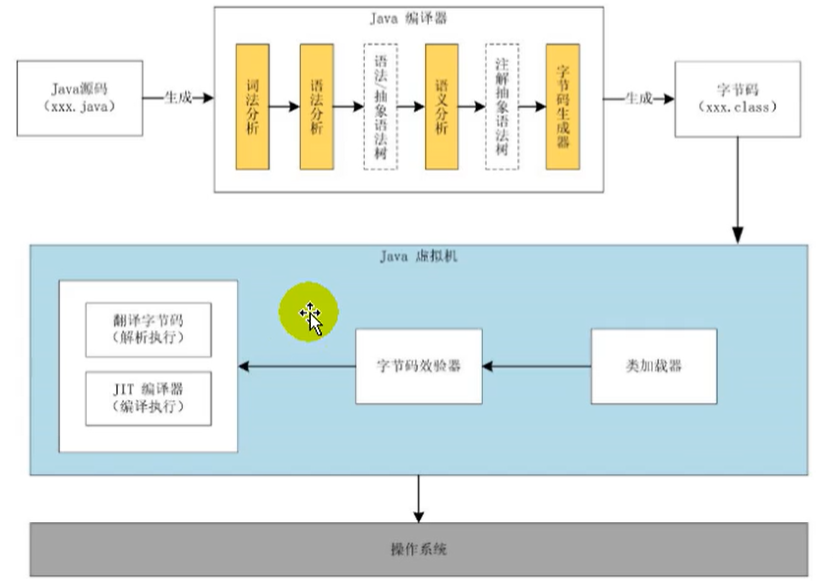
JVM和JAVA体系结构
1、为什么要学习JVM作为Java工程师的你曾被伤害过吗?你是否也遇到过这些问题?运行着的线上系统突然卡死,系统无法访问,甚至直接OOM想解决线上JVM GC问题,但却无从下手新项目上线,对各种JVM参数设置一脸茫然…...
(十)、通过云对象修改阅读量+点赞功能的实现【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,通过云对象importObj修改阅读量 1.1 新建云对象 1.2 云对象中写自增自减方法 封装云对象utilsObj中的自增自减方法,方法名取为operation,传递4个参数。 // 云对象教程: https://uniapp.dcloud.net.cn/uniCloud/cloud-obj // jsdoc语法提…...
)
刷力扣的第一天脑子要长出来的感觉(怎么有人大四才开始啊啊啊啊啊啊啊啊啊啊啊啊,又是等成绩的一天,)
刷力扣的第一天脑子要长出来的感觉(为什么大四才开始啊啊啊啊啊啊啊啊啊啊啊啊) emmm,自己还是想不太出来(只是一点想法),可能还是会参考评论区,求各位轻喷 分析:带符号一定不是回…...
Nuclei文*件上*传FUZZ POC
目录 1.前言 2. Nuclei文件上传FUZZ POC 3. 实战中的应用 1.前言 该文件上传FUZZ POC主要来源于一个靶*场,该POC 主要用来FUZZ目标js页面中的upload ajax请求,以此来进一步尝试文件上传漏*洞利*用。 这里也要感谢下“打工仔1号”提供的开*发人员常见的文*件上*传javaScr…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
