相同月利率条件下不同还款方式贷款的APR与IRR研究
文章目录
- 前提假设
- 一次性还本付息
- 先息后本
- 等额本息
- 等额本金
- 简单二分法求解IRR的程序
- 汇总
- 实验对比
前提假设
- 因为常见的信贷产品还款期数定义都是按照月,假设只借一期的利率(月利率)为r,在此条件下,研究不同还款方式下的APR和IRR计算结果与r、期数n、本金C这几个变量的关系;
- 约束条件:1)月利率为r;2)在第n期期末结束时,还清所有本息;
- IRR:根据净现值等于0时的折现率计算出实际月利率,IRR=12ractIRR=12r_{act}IRR=12ract;
- APR:年化利率,以一年(12个月)为计息长度时,利息总和占本金的百分比;
一次性还本付息
- 计算现金流:
Pi={−C,i=00,0<i<nC+Crn,i=nP_i= \begin{cases} -C, i=0 \\ 0, 0<i<n \\ C+Crn, i=n \end{cases}Pi=⎩⎨⎧−C,i=00,0<i<nC+Crn,i=n - 计算IRR:∑i=0nPi(1+ract)i=0\sum_{i=0}^{n}\frac{P_i}{(1+r_{act})^i}=0∑i=0n(1+ract)iPi=0,求得IRR=((1+rn)1/n−1)∗12IRR=((1+rn)^{1/n}-1)*12IRR=((1+rn)1/n−1)∗12;
- 计算APR:利息总和*12/C/n,求得APR=12rAPR=12rAPR=12r;
先息后本
- Pi={−C,i=0Cr,0<i<nC+Cr,i=nP_i= \begin{cases} -C, i=0 \\ Cr, 0<i<n \\ C+Cr, i=n \end{cases}Pi=⎩⎨⎧−C,i=0Cr,0<i<nC+Cr,i=n
- 计算IRR:∑i=0nPi(1+ract)i=0\sum_{i=0}^{n}\frac{P_i}{(1+r_{act})^i}=0∑i=0n(1+ract)iPi=0,−C+Cr(1(1+ract)1+...+1(1+ract)n−1)+C+Cr(1+ract)n=0-C+Cr(\frac{1}{(1+r_{act})^1}+...+\frac{1}{(1+r_{act})^{n-1}})+\frac{C+Cr}{(1+r_{act})^n}=0−C+Cr((1+ract)11+...+(1+ract)n−11)+(1+ract)nC+Cr=0,简化得(ract−r)=(ract−r)(1+ract)n(r_{act}-r)=(r_{act}-r)(1+r_{act})^n(ract−r)=(ract−r)(1+ract)n,得IRR=12rIRR=12rIRR=12r;
- 计算ARR:利息总和*12/C/n,求得APR=12rAPR=12rAPR=12r;
等额本息
- Pi={−C,i=0Cr(1+r)n(1+r)n−1,0<i<=nP_i= \begin{cases} -C, i=0 \\ C\frac{r(1+r)^n}{(1+r)^n-1}, 0<i<=n \end{cases}Pi={−C,i=0C(1+r)n−1r(1+r)n,0<i<=n
- 本质上等额本息的利息计算就是在考虑复利情况下计算出来的,所以IRR=12rIRR=12rIRR=12r;
- 计算APR:利息总和*12/C/n,求得APR=(r(1+r)n(1+r)n−1−1n)∗12APR=(\frac{r(1+r)^n}{(1+r)^n-1}-\frac{1}{n})*12APR=((1+r)n−1r(1+r)n−n1)∗12;
等额本金
- Pi={−C,i=0Cn+n+1−inCr=1+(n+1−i)rnC,0<i<=nP_i= \begin{cases} -C, i=0 \\ \frac{C}{n}+\frac{n+1-i}{n}Cr=\frac{1+(n+1-i)r}{n}C, 0<i<=n \end{cases}Pi={−C,i=0nC+nn+1−iCr=n1+(n+1−i)rC,0<i<=n
- 计算IRR:∑i=0nPi(1+ract)i=0\sum_{i=0}^{n}\frac{P_i}{(1+r_{act})^i}=0∑i=0n(1+ract)iPi=0,−C+C∑i=1n(1+(n+1−i)rn)1(1+ract)i=0-C+C\sum_{i=1}^{n}(\frac{1+(n+1-i)r}{n})\frac{1}{(1+r_{act})^i}=0−C+C∑i=1n(n1+(n+1−i)r)(1+ract)i1=0,使用数值方法求解IRR,IRR与C无关,与r和n有关;实际计算可得,近似IRR=12rIRR=12rIRR=12r;
- 计算APR:利息总和*12/C/n,求得APR=6r(n+1)nAPR=\frac{6r(n+1)}{n}APR=n6r(n+1);
简单二分法求解IRR的程序
输入:现金流list;
输出:IRR;
def cal_irr(cash_flow_list):r_min, r_max = 0,2flag = Falsecnt = 0while((flag==False)&(cnt<=100)):cnt += 1r = (r_min + r_max) / 2npv = 0for ix,i in enumerate(cash_flow_list):npv += i/(1+r)**ixif abs(npv)<=0.00001:flag = Truebreakelse:if npv>0:r_min = relse:r_max = rreturn r*12
汇总
| 还款方式 | IRR | APR |
|---|---|---|
| 一次性还本付息 | ((1+rn)1/n−1)∗12((1+rn)^{1/n}-1)*12((1+rn)1/n−1)∗12 | 12r12r12r |
| 先息后本 | 12r12r12r | 12r12r12r |
| 等额本息 | 12r12r12r | (r(1+r)n(1+r)n−1−1n)∗12(\frac{r(1+r)^n}{(1+r)^n-1}-\frac{1}{n})*12((1+r)n−1r(1+r)n−n1)∗12 |
| 等额本金 | ∑i=1n1+(n+1−i)rn(1+ract)i−1=0\sum_{i=1}^{n}\frac{1+(n+1-i)r}{n(1+r_{act})^i}-1=0∑i=1nn(1+ract)i1+(n+1−i)r−1=0的解ractr_{act}ract乘以12,≈12r\approx12r≈12r | 6r(n+1)n\frac{6r(n+1)}{n}n6r(n+1) |
实验对比
- 以月利率r(取0.005,0.01,0.03),期数n(取1、6、12、24、240),还款方式为自变量,APR和IRR为因变量,对比结果如如下。
-
IRR计算结果:
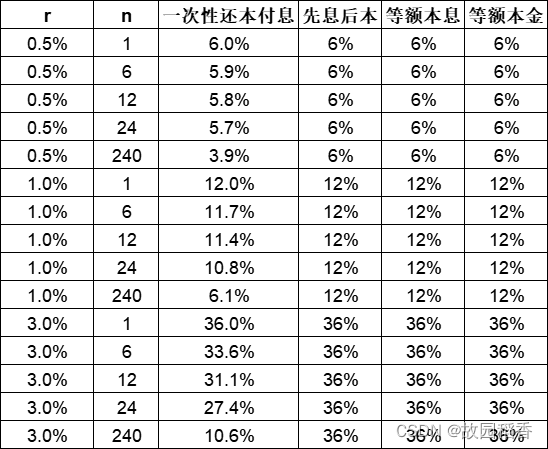
-
APR计算结果:
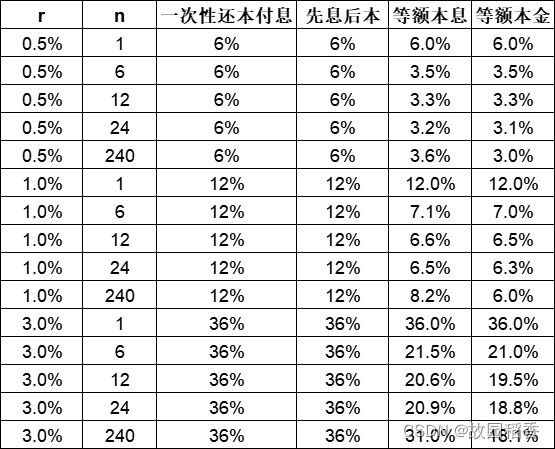
-
r=1%,n=12时,各还款方式下IRR和APR对比:

-
r=1%,等额本金和等额本息还款方式下APR随着期数n的变化:
(1)等额本金,APR随着n的增大单调递减,最终趋近6r;
(2)等额本息,APR随着n的增大先下降再上升,最终趋近12r;
(3)等额本息APR > 等额本息APR。

-
r=1%,本金C=30w,贷款36期(3年),月供流水对比:

相关文章:

相同月利率条件下不同还款方式贷款的APR与IRR研究
文章目录前提假设一次性还本付息先息后本等额本息等额本金简单二分法求解IRR的程序汇总实验对比前提假设 因为常见的信贷产品还款期数定义都是按照月,假设只借一期的利率(月利率)为r,在此条件下,研究不同还款方式下的…...

【论文】智能隧道检测车的现状及改进策略
本文转载自《智慧城轨》2022年第11期 作者:黄丹樱1,韦强1,朱椰毅2,范骁1,林浩立1 单位:1 浙江师范大学工学院;2 浙江金温铁道开发有限公司 声明:本文仅用于学术分享,不做商业用途,如有侵权,联…...

【代码随想录二刷】Day16-二叉树-C++
代码随想录二刷Day16 每日任务 104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数 语言:C 104. 二叉树的最大深度 链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/ 递归法(前序…...

Lecture5 实现线性回归(Linear Regression with PyTorch)
目录 1 Pytorch实现线性回归 1.1 实现思路 1.2 完整代码 2 各部分代码逐行详解 2.1 准备数据集 2.2 设计模型 2.2.1 代码 2.2.2 代码逐行详解 2.2.3 疑难点解答 2.3 构建损失函数和优化器 2.4 训练周期 2.5 测试结果 3 线性回归中常用优化器 1 Pytorch实现线性回归…...

Python与Matlab svd分解的差异
1.差异说明 Matlab和Python的NumPy库中的SVD函数(np.linalg.svd)都是用来对矩阵进行奇异值分解(SVD)的函数,但它们在默认参数和返回结果方面有一些差异。 在Matlab中,SVD函数的默认行为是计算矩阵的完整SVD,即对于一…...

2023年光模块行业发展趋势及未来前景
随着数字化时代的到来,互联网行业的快速发展,网络通信设备行业的发展也在逐渐加速。光模块作为网络设备的重要组成部分,也在不断创新和发展。那么,光模块行业的未来发展趋势又是怎样的呢?接下来就跟着易天光通信&#…...

Sysmac Studio使用Tortoise和Git实现版本控制
Sysmac Studio使用Tortoise和Git实现版本控制实验时间:2022/11/16 实验软件:Sysmac Studio(1.52,需要软件授权支持版本控制)、Git(2.38.1)、Tortoise(2.13.0)、gitee(代码仓库) 实验目的:Sysmac Studio实现版本控制、多人同时开…...

Intent 和 Bundle 传值的区别
文章目录1、使用上1.1 Intent 方式1.2 Bundle 方式2、为什么 Bundle 使用 ArrayMap 而不是 Hashmap 实现呢?1、使用上 1.1 Intent 方式 举例:将数据从页面 A 传递到 B,然后再传递到 CA 页面: Intent intentnew Intent(MainActi…...

TypeScript 初步
一、TypeScript是什么? Typed JavaScript at Any Scale: 添加了类型系统的JavaScript,使用于任何规模的项目。 两个重要特点: 类型系统 任何规模 中文官网:文档简介 TypeScript中文网 TypeScript——JavaScript的超集 TypeS…...
leaflet 添加zoomslider,控制zoom放大缩小(074)
第074个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用zoomslider,相比于普通的zoom控件,这个更加形象,更加具体些。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共65行)相关API参考:专栏目…...

10分钟学会python对接【OpenAI API篇】
今天学习 OpenAI API,你将能够访问 OpenAI 的强大模型,例如用于自然语言的 GPT-3、用于将自然语言翻译为代码的 Codex 以及用于创建和编辑原始图像的 DALL-E。 首先获取生成 API 密钥 在我们开始使用 OpenAI API 之前,我们需要登录我们的 Op…...

2023美赛必须注意事项
文章目录首页部分要求竞赛期间题目查看题目下载论文要求比赛提示控制号提交解决方案更多注意事项首页部分要求 具体如下: 我提取一些关键词如下: 第一页:摘要页字体要求:12点的 Times New Roman 字体请勿在此页面或任何页面上…...
基于微信小程序的智能招聘小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...

Java文件操作和I/O
Java 流(Stream)、文件(File)和IOJava.io 包几乎包含了所有操作输入、输出需要的类。所有这些流类代表了输入源和输出目标。Java.io 包中的流支持很多种格式,比如:基本类型、对象、本地化字符集等等。一个流可以理解为一个数据的序列。输入流表示从一个源…...
QT项目_RPC(进程间通讯)
QT项目_RPC(进程间通讯) 前言: 两个进程间通信、或是说两个应用程序之间通讯。实际情况是在QT开发的一个项目中,里面包含两个子程序,子程序有单独的界面和应用逻辑,这两个子程序跑起来之后需要一些数据的交互,例如&…...

移动硬盘文件丢失怎么恢复?
在我们的日常工作、学习和生活都离不开各种数据。每天都会接收或处理各种数据,尤其是做设计、自媒体、多媒体设计的人。移动硬盘成为我们常备的存储工具,但有使用就会伴随着意外情况的发生,这将导致移动硬盘上数据的丢失,比如误删…...
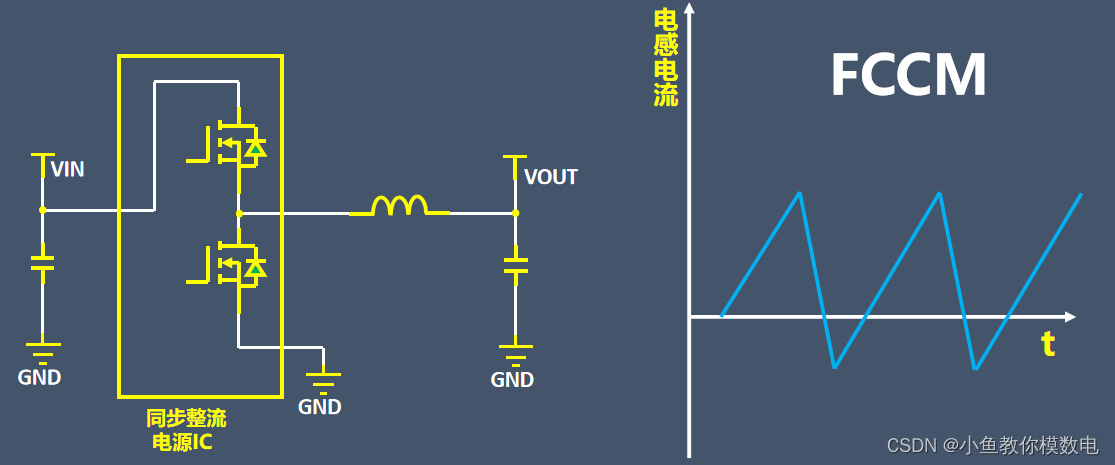
什么是同步整流和异步整流
在设计降压型DCDC电路的时候,经常会听到同步整流(synchronous)和异步整流(asynchronous)。那么什么是同步整流,什么是异步整流呢从这两种电路的拓扑来看,异步整流型外围有一个续流二极管&#x…...

关于PYTHON Enclosing 的一个小问题
问题分析 以下是一段每隔半小时重复执行测试用例的脚本,func是传入的测试函数,在执行func前后,会打印操作次数 def repeat(func, action):try:log.info(u******开始并发%s****** % action)thread_list []for i in range(repeat_count):def…...

LabVIEW错误-2147220623:最大内存块属性不存在
LabVIEW错误-2147220623:最大内存块属性不存在在使用NI Linux实时操作系统目标中,使用系统属性节点和分布式系统管理器(DSM),但遇到一些问题:它未正确报告系统上的可用物理内存量。在NI Linux实时系统上出现…...

图的总复习
一、图的定义Graph 图是由顶点vertex集合及顶点间关系集合组成的一种数据结构: 顶点的集合 和 边的集合 二、无向图 用(x,y)表示两个顶点x和y之间的一条边(edge) 边是无方向的 N{V,E},V{0…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
