数据结构与算法之二分查找分而治之思想
决定我们成为什么样人的,不是我们的能力,而是我们的选择。——《哈利·波特与密室》


二分查找是查找算法里面是很优秀的一个算法,特别是在有序的数组中,这种算法思想体现的淋漓尽致。
一.题目描述及其要求
请实现无重复数字的升序数组的二分查找:
给定一个 元素升序的、无重复数字的整型数组 arr和一个目标值 target ,写一个函数搜索 arr中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1.
示例一:
输入:[-1,0,3,4,6,10,13,14],13
返回值:6
说明:13 出现在arr中并且下标为 6 示例二:
输入:[],3
返回值:-1
说明:arr为空,返回-1 示例三:
输入:[-1,0,3,4,6,10,13,14],2
返回值:-1
说明:2 不存在arr中因此返回 -1 二.分治思想
分治即“分而治之”,“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题,子问题继续按照这样划分,直到问题可以被轻易解决;“治”指的是将子问题单独进行处理。经过分治后的子问题,需要将解进行合并才能得到原问题的解,因此整个分治过程经常用递归来实现。
1.逐个遍历思路:
本来我们可以遍历数组直接查找,每次检查当前元素是不是要找的值。
for(int i = 0; i <length; i++)if(arr[i] == target)return i;2.逐个遍历出现的问题
但是这样这个有序的数组我们就没有完全利用起来。
我们想想,若是目标值比较小,肯定在前半区间,若是目标值比较大,肯定在后半区间,怎么评价大小?我们可以用中点值作为一个标杆,将整个数组分为两个区间,目标值与中点值比较就能知道它会在哪个区间,这就是分治的思维。
三分治思想具体做法:
step 1:从数组首尾开始,每次取中点值。
step 2:如果中间值等于目标即找到了,可返回下标,如果中点值大于目标,说明中点以后的都大于目标,因此目标在中点左半区间,如果中点值小于目标,则相反。
step 3:根据比较进入对应的区间,直到区间左右端相遇,意味着没有找到
代码实现:
int search(int*arr, int length, int target ) {if(length == 0) return -1;int left=0, right=length-1;while(left<=right) {int mid = left+(right-left)/2;if(arr[mid]==target) return mid;if(arr[mid]<target) left=mid+1;if(arr[mid]>target) right=mid-1;}return -1;
}
ps:int mid = left+(right-left)/2;与int mid=(left+right)/2是一样的,但是选择前者更安全,因为后者两个整数相加数据过于庞大可能会出现数据溢出的情况,所以采用前者更加可靠。
也可以这样写:mid = left+(right-left >> 1); +-大于位移运算的优先级 左移*2
本算法到这,其实二分查找可以分为几种情况来讨论,这里提供一种比较好理解的方案,具体算法大家可以参考相应资料自了解,大家加油。。。。。最近在做算法题目可以关注我,点个赞,有问题可以一起讨论。以后的几篇文章都讲解算法的题目。
相关文章:

数据结构与算法之二分查找分而治之思想
决定我们成为什么样人的,不是我们的能力,而是我们的选择。——《哈利波特与密室》二分查找是查找算法里面是很优秀的一个算法,特别是在有序的数组中,这种算法思想体现的淋漓尽致。一.题目描述及其要求请实现无重复数字的升序数组的…...
训练自己的中文word2vec(词向量)--skip-gram方法
训练自己的中文word2vec(词向量)–skip-gram方法 什么是词向量 将单词映射/嵌入(Embedding)到一个新的空间,形成词向量,以此来表示词的语义信息,在这个新的空间中,语义相同的单…...

ubuntu系统环境配置和常用软件安装
系统环境 修改文件夹名称为英文 参考链接 export LANGen_US xdg-user-dirs-gtk-update 常用软件安装 常用工具 ping 和ifconfig工具 sudo apt install -y net-tools inetutils-ping 截图软件 sudo apt install -y net-tools inetutils-ping flameshot 录屏 sudo apt-get i…...
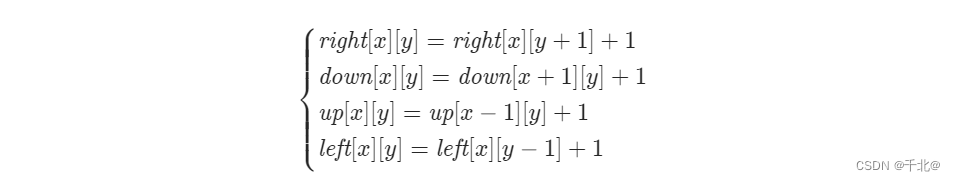
【1139. 最大的以 1 为边界的正方形】
来源:力扣(LeetCode) 描述: 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1&#…...
windows11安装sqlserver2022报错
window11安装SQL Server 2022 报错 糟糕… 无法安装SQL Server (setup.exe)。此 SQL Server安装程序介质不支持此OS的语言,或没有SQL Server英语版本的安装文件。请使用匹配的特定语言SQL Server介质;或安装两个特定语言MUI,然后通过控制面板的区域设置…...

Python快速上手系列--日志模块--详解篇
前言本篇主要说说日志模块,在写自动化测试框架的时候我们就需要用到这个模块了,方便我们快速的定位错误,了解软件的运行情况,更加顺畅的调试程序。为什么要用到日志模块,直接print不就好了!那得写多少print…...

【THREE.JS学习(1)】绘制一个可以旋转、放缩的立方体
学习新技能,做一下笔记。在使用ThreeJS的时候,首先创建一个场景const scene new THREE.Scene();接着,创建一个相机其中,THREE.PerspectiveCamera()四个参数分别为:1.fov 相机视锥体竖直方向视野…...
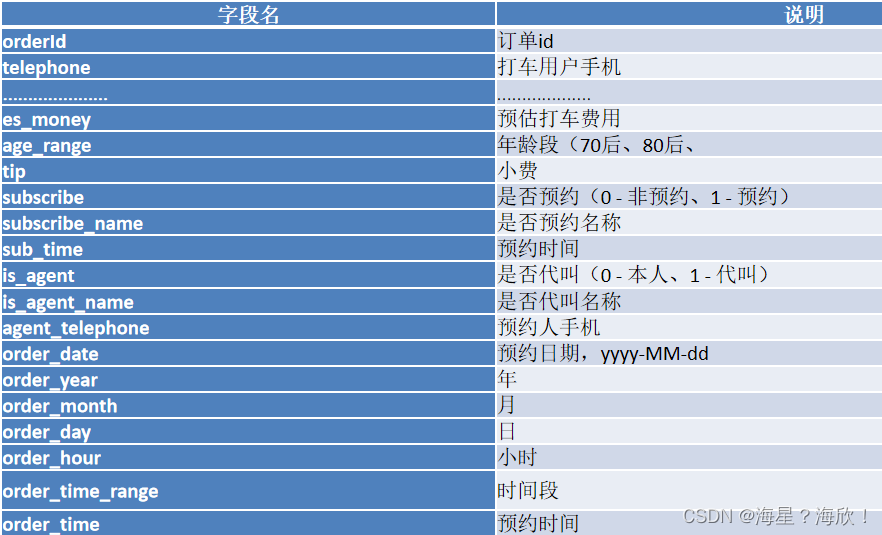
数仓实战 - 滴滴出行
项目大致流程: 1、项目业务背景 1.1 目的 本案例将某出行打车的日志数据来进行数据分析,例如:我们需要统计某一天订单量是多少、预约订单与非预约订单的占比是多少、不同时段订单占比等 数据海量 – 大数据 hive比MySQL慢很多 1.2 项目架…...
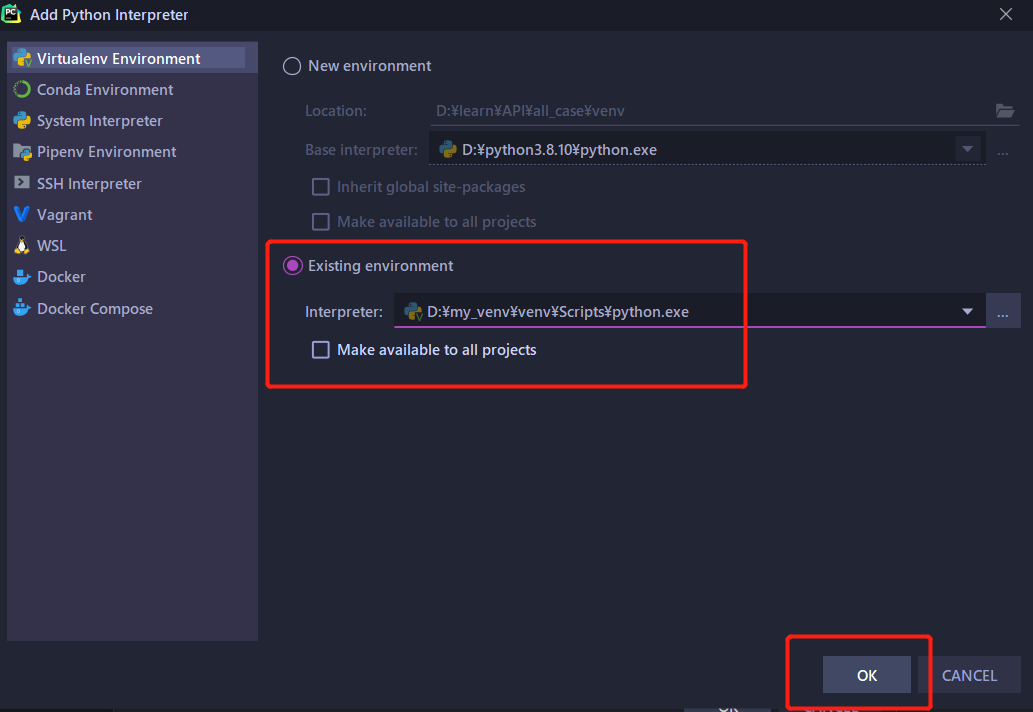
python虚拟环境与环境变量
一、环境变量 1.环境变量 在命令行下,使用可执行文件,需要来到可执行文件的路径下执行 如果在任意路径下执行可执行文件,能够有响应,就需要在环境变量配置 2.设置环境变量 用户变量:当前用户登录到系统,…...

BeautifulSoup文档4-详细方法 | 用什么方法对文档树进行搜索?
4-详细方法 | 用什么方法对文档树进行搜索?1 过滤器1.1 字符串1.2 正则表达式1.3 列表1.4 True1.5 可以自定义方法2 find_all()2.1 参数原型2.2 name参数2.3 keyword 参数2.4 string 参数2.5 limit 参数2.6 recursive 参数3 find()4 find_parents()和find_parent()5…...

初识Tkinter界面设计
目录 前言 一、初识Tkinter 二、Label控件 三、Button控件 四、Entry控件 前言 本文简单介绍如何使用Python创建一个界面。 一、初识Tk...

软件测试面试题中的sql题目你会做吗?
目录 1.学生表 2.一道SQL语句面试题,关于group by表内容: 3.表中有A B C三列,用SQL语句实现:当A列大于B列时选择A列否则选择B列,当B列大于C列时选择B列否则选择C列 4. 5.姓名:name 课程:subject 分数&…...

VS实用调试技巧
一.什么是BUG🐛Bug一词的原意是虫子,而在电脑系统或程序中隐藏着的一些未被发现的缺陷或问题,人们也叫它"bug"。这是为什么呢?这就要追溯到一个程序员与飞蛾的故事了。Bug的创始人格蕾丝赫柏(Grace Murray H…...
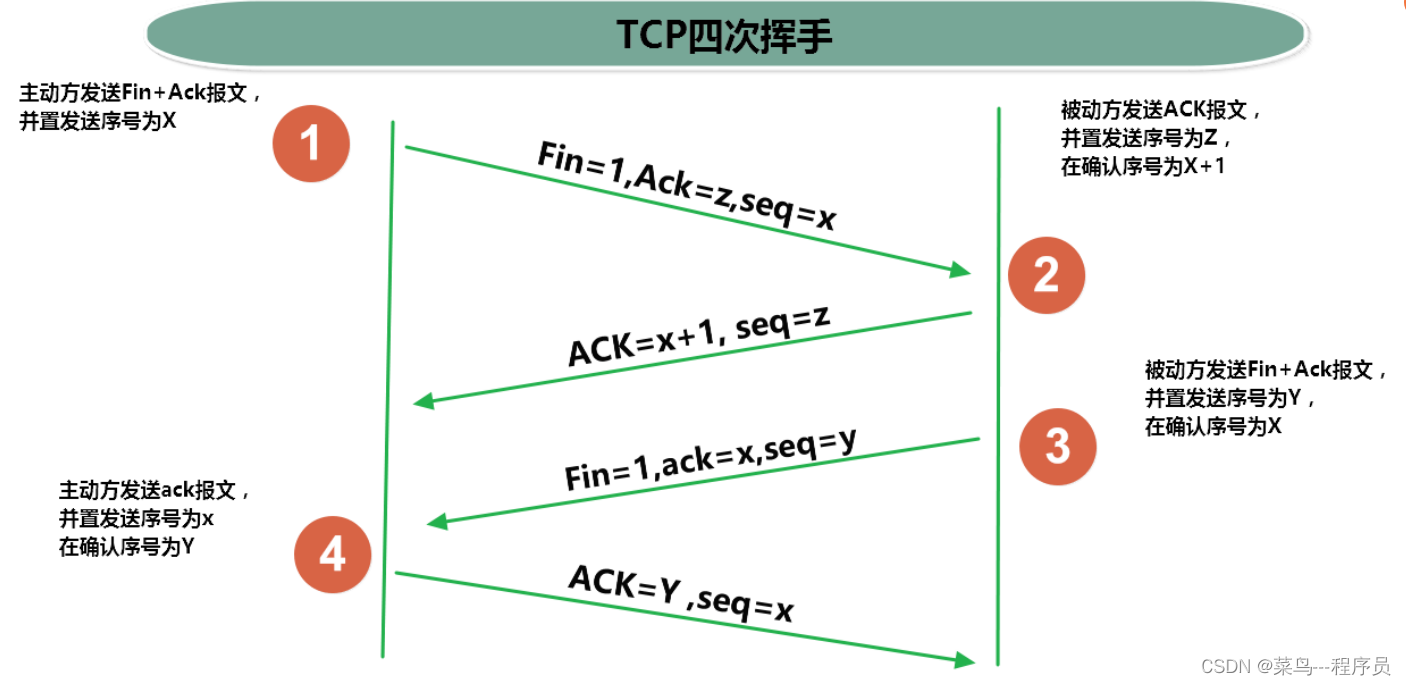
通俗易懂理解三次握手、四次挥手(TCP)
文章目录1、通俗语言理解1.1 三次握手1.2 四次挥手2、进一步理解三次握手和四次挥手2.1 三次握手2.2 四次挥手1、通俗语言理解 1.1 三次握手 C:客户端 S:服务器端 第一次握手: C:在吗?我要和你建立连接。 第二次握手ÿ…...
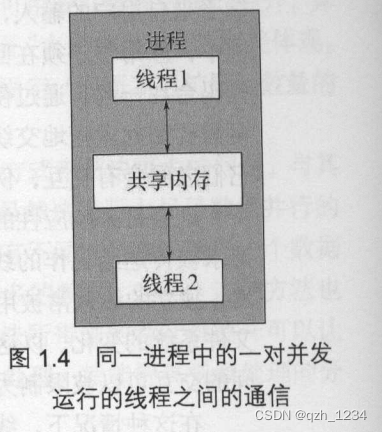
1.1 什么是并发
1.1 什么是并发 并发:指两个或更多独立的活动同时发生。并发在生活中随处可见。我们可以一边走路一边说话,也可以两只手同时做不同的动作。 1.1.1 计算机系统中的并发 当我们提到计算机术语的“并发”,指的是在单个系统里同时执行多个独立…...

万字讲解你写的代码是如何跑起来的?
今天我们来思考一个简单的问题,一个程序是如何在 Linux 上执行起来的? 我们就拿全宇宙最简单的 Hello World 程序来举例。 #include <stdio.h> int main() {printf("Hello, World!\n");return 0; } 我们在写完代码后,进行…...

034.Solidity入门——21不可变量
Solidity 中的不可变量是在编译时就被确定的常量,也称为常量变量(constant variable)或只读变量(read-only variable)。这些变量在定义时必须立即初始化,并且在整个合约中都无法被修改,可以在函…...
Vulnhub 渗透练习(四)—— Acid
环境搭建 环境下载 kail 和 靶机网络适配调成 Nat 模式,实在不行直接把网络适配还原默认值,再重试。 信息收集 主机扫描 没扫到,那可能端口很靠后,把所有端口全扫一遍。 发现 33447 端口。 扫描目录,没什么有用的…...

C++ 在线工具
online编译器https://godbolt.org/Online C Compiler - online editor (onlinegdb.com) https://www.onlinegdb.com/online_c_compilerC Shell (cpp.sh) https://cpp.sh/在线文档Open Standards (open-std.org)Index of /afs/cs.cmu.edu/academic/class/15211/spring.96/wwwC P…...

使用MMDetection进行目标检测、实例和全景分割
MMDetection 是一个基于 PyTorch 的目标检测开源工具箱,它是 OpenMMLab 项目的一部分。包含以下主要特性: 支持三个任务 目标检测(Object Detection)是指分类并定位图片中物体的任务实例分割(Instance Segmentation&a…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
