【深度学习】多分类问题和多标签分类问题
上一章——激活函数
文章目录
- 什么是多分类问题
- Softmax
- 贝叶斯公式
- softmax的损失函数
- 多标签分类问题
什么是多分类问题
 在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是在大多数情况下,分类问题的输出远远不止两种情况,例如之前在课程中举例的肿瘤问题,肿瘤被分为良性和恶性两种,但实际上会有更多的分类情况,它有可能是A型,B型,C型…我们将这种拥有2种以上输出标签的问题称为多分类问题。虽然输出y依旧只能取值有限的离散值,但是输出标签的种类将会有两个以上。
在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是在大多数情况下,分类问题的输出远远不止两种情况,例如之前在课程中举例的肿瘤问题,肿瘤被分为良性和恶性两种,但实际上会有更多的分类情况,它有可能是A型,B型,C型…我们将这种拥有2种以上输出标签的问题称为多分类问题。虽然输出y依旧只能取值有限的离散值,但是输出标签的种类将会有两个以上。
MNIST被称为机器学习的“Hello World”,MNIST要求算法识别出不同的字迹所对应的数字,所有的阿拉伯数字总共有10个(0~9),MNIST就是一个典型的多分类问题。
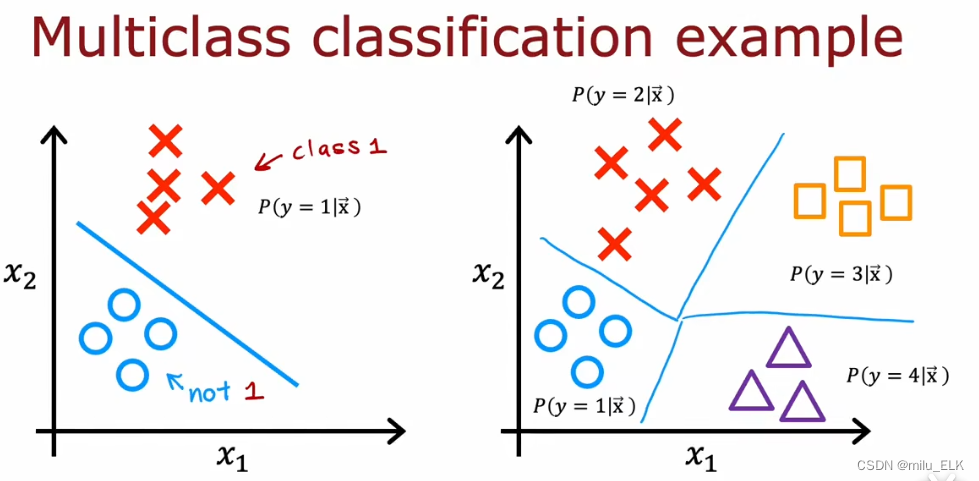
在二分问题中,我们的拟合方法是找到假设函数g(z)g(z)g(z)中的决策边界z,那么推广到多分类问题中,也是同样的方法,二分问题只需一条决策边界,而往后的n分问题则需要n条决策边界。类比二分问题中我们使用的是逻辑回归,在多分问题中我们将学习Softmax算法。
Softmax
Softmax算法是对逻辑回归的推广和泛化,是一种针对多分类环境下的二元分类算法

首先我们要指出一点:所有离散值的预测概率之和一定为1。
以二分问题中的逻辑回归为例,假设P(y=1∣x)=0.71P(y=1|x)=0.71P(y=1∣x)=0.71,那么P(y=0∣x)=1−0.71=0.29P(y=0|x)=1-0.71=0.29P(y=0∣x)=1−0.71=0.29,
这个很好理解,因为输出结果不是0就是1,那么P(y=1∣x)+P(y=0∣x)=1P(y=1|x)+P(y=0|x)=1P(y=1∣x)+P(y=0∣x)=1,那么我们推广到多元


我们会发现Softmax的计算公式与Sigmoid相似,
Softmax:zj=w⃗j⋅x⃗+bj(j=1...N)z_j=\vec w_j \cdot \vec x+b_j(j=1...N)zj=wj⋅x+bj(j=1...N)
aj=ezj∑k=1Nezk=P(y=j∣x⃗)a_j=\frac{e^{z_j}}{\sum^N_{k=1} e^{z_k}}=P(y=j|\vec x)aj=∑k=1Nezkezj=P(y=j∣x)
如果想要从数学上理解Softmax函数,我们必须先了解一个概念:
- 贝叶斯公式
贝叶斯公式
条件概率公式:
P(x∣y)=P(xy)P(y)P(x|y)=\frac {P(xy)}{P(y)}P(x∣y)=P(y)P(xy)
其中P(x∣y)P(x|y)P(x∣y)代表在y事件已经发生的情况下x事件发生的概率,P(xy)P(xy)P(xy)代表事件xy都发生的概率,P(y)代表y事件发生的概率(无论x事件是否发生)
全概率公式:
P(x)=∑i=1nP(yi)P(x∣yi)P(x)=\displaystyle\sum^n_{i=1}P(y_i)P(x|y_i)P(x)=i=1∑nP(yi)P(x∣yi)
因此x事件发生的全概率是在每一种yiy_iyi事件发生的情况下事件x发生的概率之和
贝叶斯公式:
P(yi∣x)=P(x∣yi)P(yi)P(x)=P(x∣yi)P(yi)∑j=1nP(yi)P(x∣yj)P(y_i|x)=\frac {P(x|y_i)P(y_i)}{P(x)}=\frac {P(x|y_i)P(y_i)}{\sum^n_{j=1}P(y_i)P(x|y_j)}P(yi∣x)=P(x)P(x∣yi)P(yi)=∑j=1nP(yi)P(x∣yj)P(x∣yi)P(yi)
其中根据条件概率公式我们知道P(x∣yi)P(yi)=P(xyi),P(x|y_i)P(y_i)=P(xy_i),P(x∣yi)P(yi)=P(xyi),即为x和yiy_iyi事件都发生的概率,P(x)为x事件发生的全概率
因此P(yi∣x)=P(xyi)P(x)P(y_i|x)=\frac {P(xy_i)}{P(x)}P(yi∣x)=P(x)P(xyi)
在二分类问题中,由于分类只有两种,因此事件y只有两项,如果我们将贝叶斯公式上下同时除以P(y1)P(x∣y1)P(y_1)P(x|y_1)P(y1)P(x∣y1):
P(y1∣x)=P(y1)P(x∣y1)P(y1)P(x∣y1)+P(y2)P(x∣y2)P(y_1|x)=\frac {P(y_1)P(x|y_1)}{P(y_1)P(x|y_1)+P(y_2)P(x|y_2)}P(y1∣x)=P(y1)P(x∣y1)+P(y2)P(x∣y2)P(y1)P(x∣y1)
=11+P(y2)P(x∣y2)P(y1)P(x∣y1)=\frac {1}{1+\frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)}}=1+P(y1)P(x∣y1)P(y2)P(x∣y2)1
我们将P(y2)P(x∣y2)P(y1)P(x∣y1)\frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)}P(y1)P(x∣y1)P(y2)P(x∣y2)设为e−ze^{-z}e−z
P(y1∣x)=11+e−zP(y_1|x)=\frac {1}{1+e^{-z}}P(y1∣x)=1+e−z1
是不是有点眼熟?没错,这就是Sigmoid函数,
其中z=lnP(y2)P(x∣y2)P(y1)P(x∣y1)z=ln\frac {P(y_2)P(x|y_2)}{P(y_1)P(x|y_1)}z=lnP(y1)P(x∣y1)P(y2)P(x∣y2),z与向量的关系请参考sigmoid与条件概率的关系及推导过程
之所以要设成e的指数形式,是为了防止概率出现负数,以e的指数形式表示是不会出现负数的
我们说softmax是Sigmoid的推广,你可以简单地把P(y1∣x)看作t1t1+t2,P(y_1|x)看作\frac {t_1}{t_1+t_2},P(y1∣x)看作t1+t2t1,则P(y2∣x)=1−t1t1+t2=t2t1+t2P(y_2|x)=1-\frac {t_1}{t_1+t_2}=\frac {t_2}{t_1+t_2}P(y2∣x)=1−t1+t2t1=t1+t2t2,然后推广到n阶就有P(yN∣x)=tNt1+...+tNP(y_N|x)=\frac {t_N}{t_1+...+t_N}P(yN∣x)=t1+...+tNtN,当然我只是从结果上讲,没有什么数学推理,具体原理贴在下面链接
本文只是简单地提一下概率论的一些基本知识,至于softmax公式的推导,如果还想深究里面的数学原理,可以看看这个视频,作者本人打算学完这个系列之后在复习这些内容:softmax是为了解决归一问题凑出来的吗?和最大熵是什么关系?最大熵对机器学习为什么非常重要?
softmax的损失函数
回到我们上面的内容,Softmax:
zj=w⃗j⋅x⃗+bj(j=1...N)z_j=\vec w_j \cdot \vec x+b_j(j=1...N)zj=wj⋅x+bj(j=1...N)
aj=ezj∑k=1Nezk=P(y=j∣x⃗)a_j=\frac{e^{z_j}}{\sum^N_{k=1} e^{z_k}}=P(y=j|\vec x)aj=∑k=1Nezkezj=P(y=j∣x)
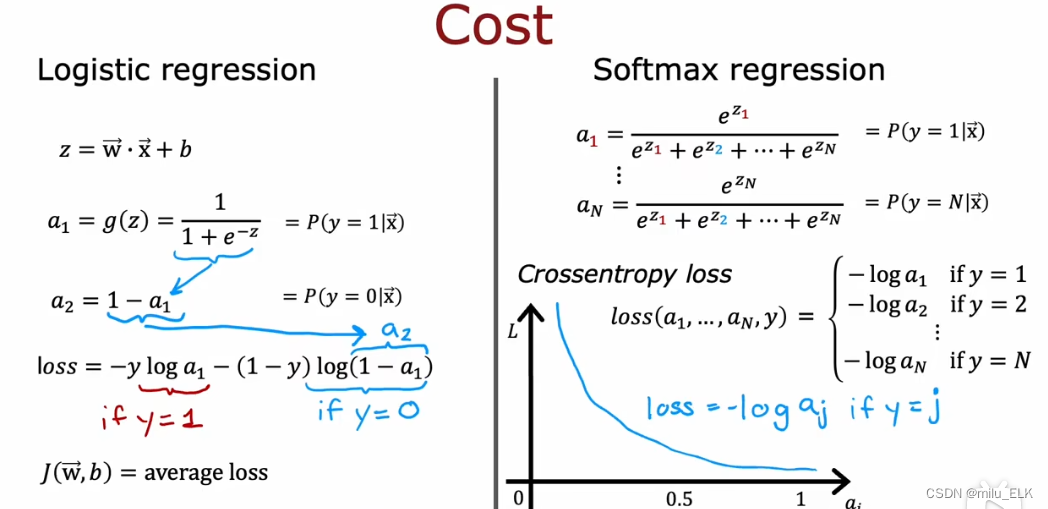
我们说Softmax是逻辑回归的推广,那么其损失函数也应当类似,
其中loss(a1,....aN,y)={−loga1ify=1−loga2ify=2...−logaNify=Nloss(a_1,....a_N,y)= \begin{cases} -log\space a_1 \space\space if \space y=1 \\ -log\space a_2 \space\space if \space y=2 \\ ... \\ -log\space a_N \space\space if \space y=N \end{cases}loss(a1,....aN,y)=⎩⎨⎧−log a1 if y=1−log a2 if y=2...−log aN if y=N
当概率aia_iai越接近0,损失越大,其中N代表单层内神经元的个数
多标签分类问题
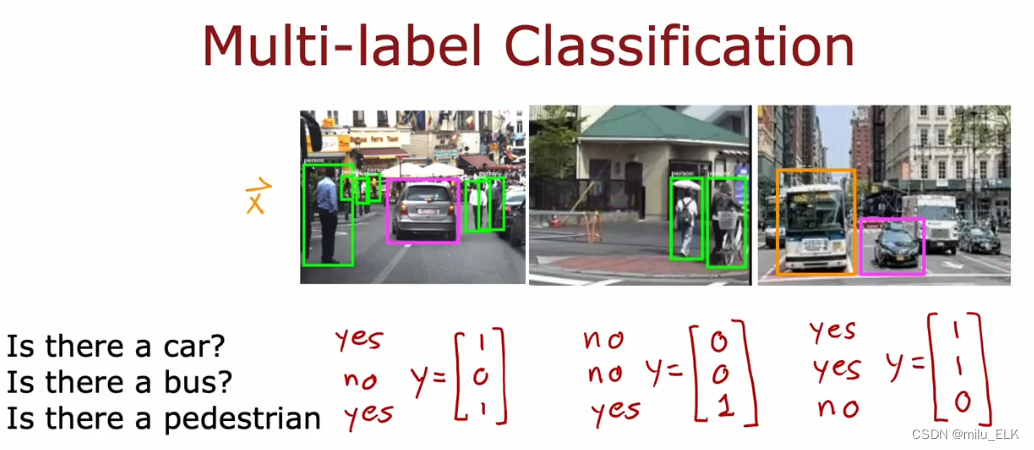
如果我们想要用人工智能来实现视觉识别,就像你平时在上网时遇到的一些验证题目:“为了验证您不是机器人,请找出图中的汽车”。我们想要实现对一张图片同时多处进行识别,以上图为例,识别图中是否有轿车?是否有公交车?是否有行人?
那么该例子中输入图片x,我们将会得到一个含三个数字的输出向量y。
注意:多标签分类问题和我们在上面所说的多分类问题并不是同一个东西,在多分类问题中,尽管有多种不同的取值,但我们最后得到的输出结果往往是数字y。其本质回答的是一个问题:预测值属于哪一类?
而在多标签分类问题中,最终的输出结果是一个含多个数字的向量,这意味着你可以认为它同时解答了多个问题:是否存在a?是否存在b?…是否存在n?在多分类问题中,最终结果只能是多个标签中的一个,但在多标签分类问题中最终结果可能是多个标签同时存在。
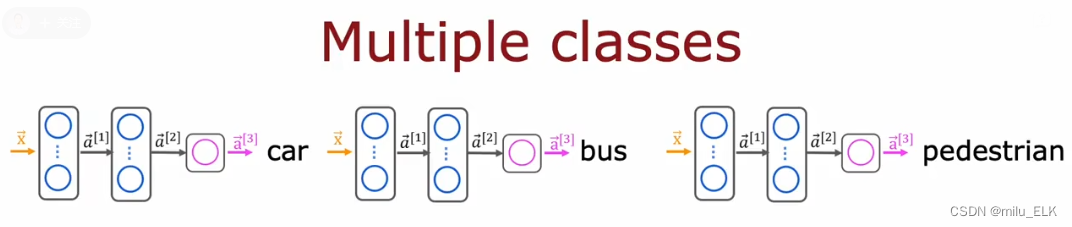
我们怎样去实现多标签分类问题?如果说回答三个问题,我们当然可以设计三个神经网络,来分别解决。但是这样未免也太浪费了,实际上由于这三个问题的结构都是一模一样的,本质上来说都是同样的算法,它们的隐藏层都是一样的,因此我们可以将它们进行合并。
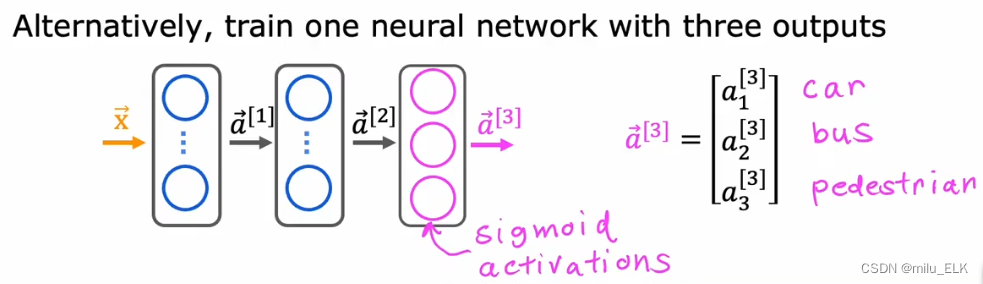
最终,我们可以构造这样的一个神经网络,唯一的区别在于输出层使用了多个神经元而非单个,相当于我们将上面的三个神经网络的输出层的神经元合并到同一个输出层。而且注意:在此处我们使用的是Sigmoid函数而非Softmax。不是说Softmax用于解决多个标签的分类问题吗?因为本质上该例子中需要预测的问题是三个二分问题,所以我们使用的是三个Sigmoid函数而非Softmax。
在学习中,不要搞混了多分类问题和多标签分类问题的概念。你可以简单理解为:多分类问题中的所有输出标签都是互斥的,如果是A那就不能是B、C…
而在多标签分类问题中,所有的输出标签并无互斥关系,输出有A也不影响输出B,它们可以同时存在。
相关文章:

【深度学习】多分类问题和多标签分类问题
上一章——激活函数 文章目录什么是多分类问题Softmax贝叶斯公式softmax的损失函数多标签分类问题什么是多分类问题 在之前的课程中,我们学习了二分问题,二分问题中的所有数据会被分类为0和1(或者Ture和False)两种输出标签。但是…...

大学生开学买什么,返校必备数码好物推荐
开学还不知道需要准备些什么,这篇开学数码好物,希望能够对你在开学购买的好物有一些帮助,一款好的数码装备,可以让我们在学校学习当中能够用最少的时间,最大的产出,节省时间,提高学习效率&#…...
Unreal Engine06:Actor的实现
写在前面 Actor是可以放进地图的最基本类,这里主要是介绍一下Actor的使用。 一、空间坐标系 1. Actor的变换操作 Actor的变换变换操作主要包括四个部分: 位置;旋转;缩放; 上面三者都是对应三个轴进行变换࿱…...
2023美国大学生数学建模竞赛C题思路解析(含代码+数据可视化)
以下为2023美国大学生数学建模竞赛C题思路解析(含代码数据可视化)规则:猜词,字母猜对,位置不对为黄色,位置对为绿色,两者皆不对为灰色。困难模式下的要求:对于猜对的字母(…...
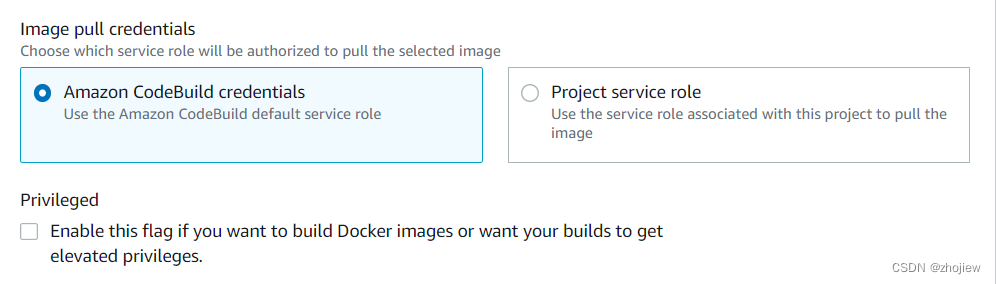
aws codebuild 自定义构建环境和本地构建
参考资料 Extending AWS CodeBuild with Custom Build Environments Docker in custom image sample for CodeBuild codebuild自定义构建环境 在创建codebuild项目的时候发现 构建环境是 Docker 映像,其中包含构建和测试项目所需的所有内容的完整文件系统 用ru…...
3年功能3年自动化,从8k到23k的学习过程
简单的先说一下,坐标杭州,14届本科毕业,算上年前在阿里巴巴的面试,一共有面试了有6家公司(因为不想请假,因此只是每个晚上去其他公司面试,所以面试的公司比较少)其中成功的有4家&…...

leaflet: 数据聚合,显示当前bounds区域中的点的名称列表(078)
第078个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中实现数据聚合的功能 ,左边列出右边可视区域内的marker的名称。这里主要用到了可视区域的范围以及contains函数。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方…...
XXL-JOB分布式任务调度框架(一)-基础入门
文章目录1.什么是任务调度2.常见定时任务方案2.1. 传统定时任务方案示例2.2. 缺点分析3.什么是分布式任务调度?3.1. 并行任务调度3.2. 高可用3.3. 弹性扩容3.4. 任务管理与监测4.市面上常见的分布式任务调度产品5.初识xxl-job6.xxl-job架构设计6.1.设计思想6.2.架构…...

基于CentOS 7 搭建Redis 7集群
我们的目标是使用2台(多台服务器类似)服务器搭建一个3主3从的redis集群。 我们为什么要使用redis 7呢?因为6、7的版本都做了大量优化,比如6引入了多线程(一些JAVA八股文面试还喜欢问redis为什么是单线程)&…...

Lesson5.3---Python 之 NumPy 统计函数、数据类型和文件操作
一、统计函数 NumPy 能方便地求出统计学常见的描述性统计量。最开始呢,我们还是先导入 numpy。 import numpy as np1. 求平均值 mean() mean() 是默认求出数组内所有元素的平均值。我们使用 np.arange(20).reshape((4,5)) 生成一个初始值默认为 0,终止…...
Puppeteer 爬虫学习
puppeteer简介: Puppeteer 是一个 Node 库,它提供了一个高级 API 来通过 DevTools 协议 控制 Chromium 或 Chrome。Puppeteer 默认以 headless 模式运行, 但是可以通过修改配置文件运行“有头”模式。能作什么?: 生成…...
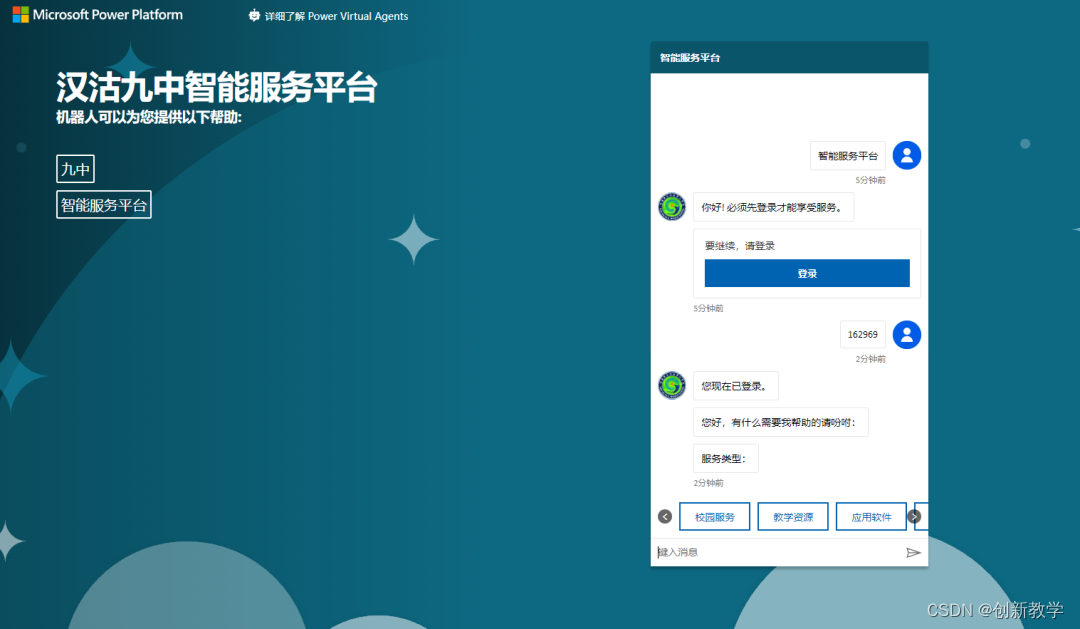
如何在Power Virtual Agents中实现身份验证
今天我们介绍一下如何通过身份验证的方式来使用Power Virtual Agents。首先进入“Microsoft 365-管理-Azure Active Directory管理中心”。 进入“Azure Active Directory管理中心”后选择“Azure Active Directory”中的“应用注册”-“新注册”。 输入新创建的应用程序名称后…...

金三银四必备软件测试必问面试题
初级软件测试必问面试题1、你的测试职业发展是什么?测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前 3 年积累测试经验,按如何做好测试工程…...
Java反序列化漏洞——CommonsCollections6链分析
一、前因因为在jdk8u71之后的版本中,sun.reflect.annotation.AnnotationInvocationHandler#readObject的逻辑发生了变化,导致CC1中的两个链条都不能使用,所有我们需要找一个在高版本中也可用的链条。/* Gadget chain: java.io.ObjectInputStr…...

Selenium浏览器自动化测试框架
Selenium浏览器自动化测试框架 目录:导读 1、selenium简介 介绍 功能 优势 2、基本使用 3、获取单节点 4、获取多节点 5、节点交互 6、动作链 7、执行JavaScript代码 8、获取节点信息 9、切换frame 10、延时等待 11、前进和后退 12、cookies 13、选…...
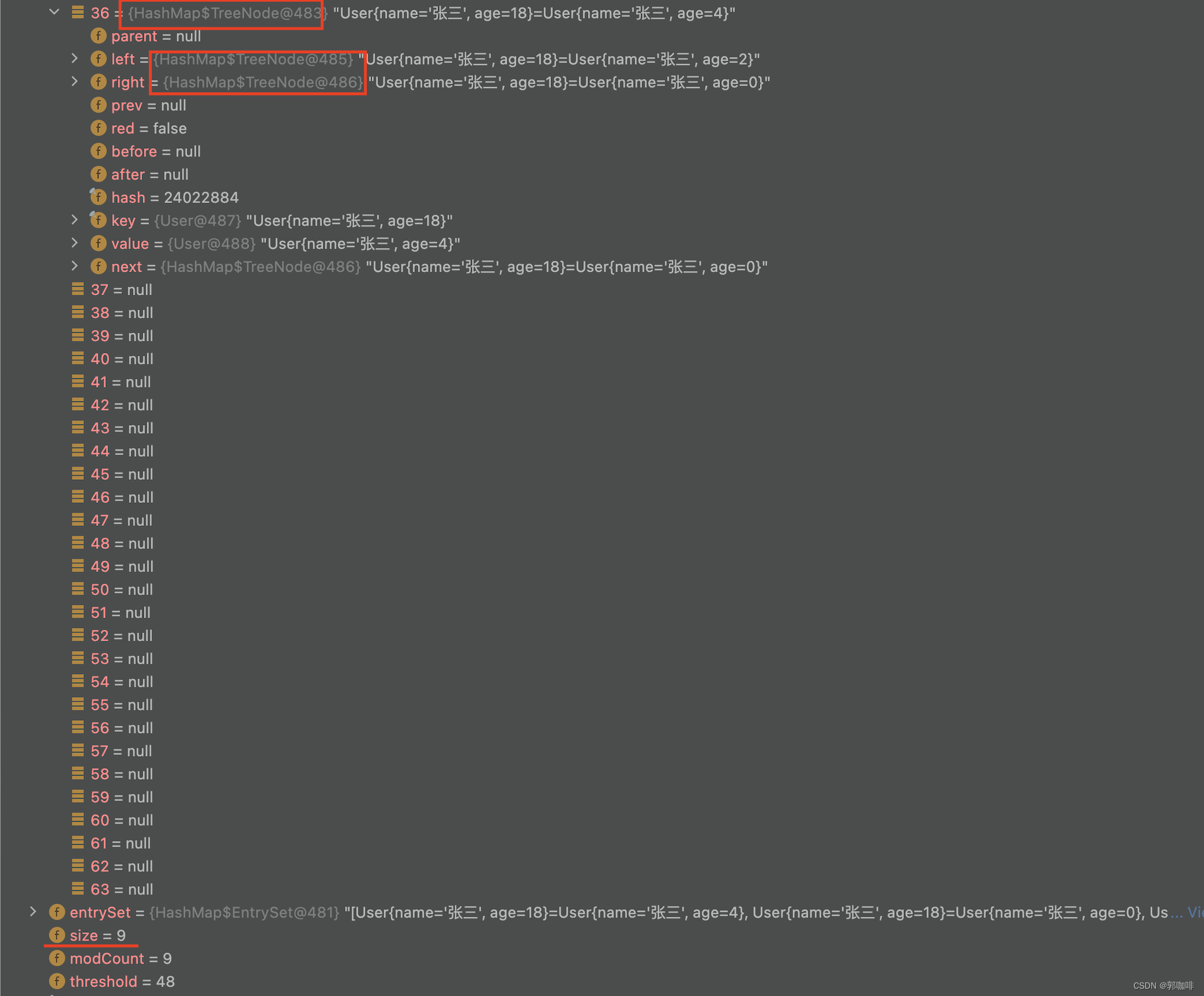
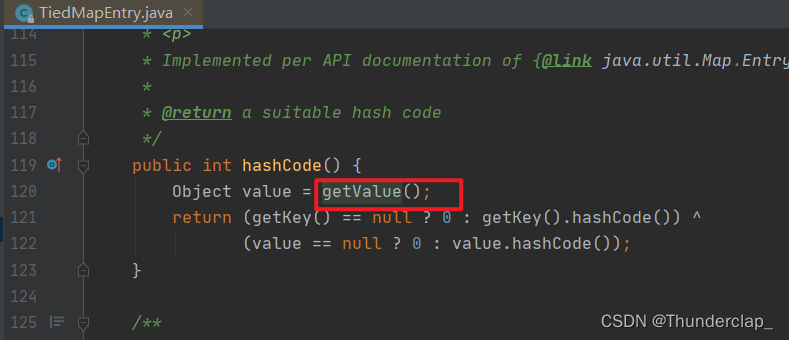
Hashmap链表长度大于8真的会变成红黑树吗?
1、本人博客《HashMap、HashSet底层原理分析》 2、本人博客《若debug时显示的Hashmap没有table、size等元素时,查看第19条》 结论 1、链表长度大于8时(插入第9条时),会触发树化(treeifyBin)方法,但是不一定会树化,若数组大小小于…...

关于接地:数字地、模拟地、信号地、交流地、直流地、屏蔽地、浮地
除了正确进行接地设计、安装,还要正确进行各种不同信号的接地处理。控制系统中,大致有以下几种地线: (1)数字地:也叫逻辑地,是各种开关量(数字量)信号的零电位。 (2&am…...

排序
一、数据流中的中位数题目描述:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。…...
Android DataStore Proto存储接入流程详解与使用
一、介绍 通过前面的文字,我们已掌握了DataStore 的存储,但是留下一个尾巴,那就是Proto的接入。 Proto是什么? Protobuf,类似于json和xml,是一种序列化结构数据机制,可以用于数据通讯等场景&a…...

HiEV洞察 | 卖一台亏半台,激光雷达第一股禾赛隐忧仍在
作者 | 感知君Alex 编辑 | 王博2月9日晚,禾赛在万众瞩目下登陆纳斯达克,发行价19美元每股,首日涨超11%,市值超过Luminar,登顶全球市值最高的激光雷达公司。 随后两个交易日,其股价均有不同程度的涨幅&#…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

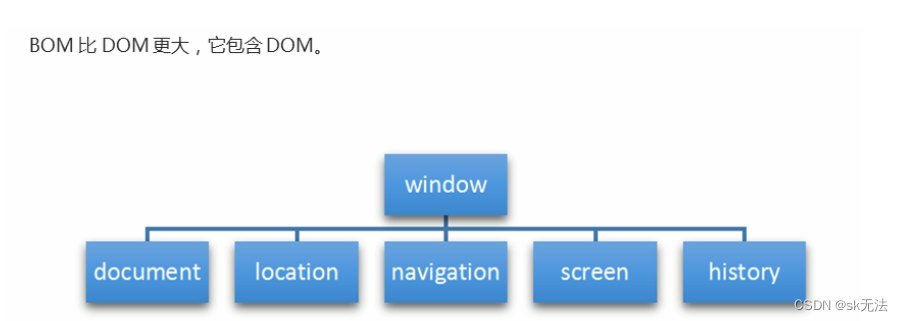
【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
