排序
一、数据流中的中位数
题目描述:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
解题思路:这里考虑到是从数据流中获取,那么数据就是不断更新的。使用大顶堆来存放排序后前半部分(小的数),使用小顶堆来存放排序后的后半部分(大的数)。其中需要注意的是以下堆的几个操作:
将元素入堆:m.push_back(x);
向堆中添加新的元素作为叶子节点:push_heap(m.begin(),m.end(),less<int>())
堆顶元素出堆:
pop_heap(m.begin(),m.end(),less<int>())
m.pop_back()
classSolution {
private:vector<int>max;vector<int>min;
public:voidInsert(int num){int size=max.size()+min.size(); //统计整个数据的长度if((size&1)==0) //这里先判断奇偶性,如果是奇数个数字,则遍历大顶堆,统计前半部分数组。{if(max.size()>0&&num<max[0]){max.push_back(num);push_heap(max.begin(),max.end(),less<int>()); //添加数据流中的新元素,作新的叶节点num=max[0]; //获取堆顶元素以便放到后半部分数据组成的小顶堆中pop_heap(max.begin(),max.end(),less<int>()); //堆顶元素出堆max.pop_back();}//将大顶堆中的堆顶元素放到小顶堆中以便平衡元素min.push_back(num);push_heap(min.begin(),min.end(),greater<int>());}else{if(min.size()>0&&num>min[0]){min.push_back(num);push_heap(min.begin(),min.end(),greater<int>()); //添加数据流中的新元素num=min[0]; //获取堆顶元素以便放到前半部分数据组成的大顶堆中pop_heap(min.begin(), min.end(),greater<int>()); //堆顶元素出堆min.pop_back();}//将小顶堆中的堆顶元素放到大顶堆中以便平衡元素max.push_back(num);push_heap(max.begin(), max.end(),less<int>()); //堆顶元素出堆}}doubleGetMedian(){int size=max.size()+min.size();if(size<=0) return0;if((size&1)==0) //判断奇偶性return (max[0]+min[0])/2.0;elsereturn min[0];}};
二、最小的K个数
题目描述:输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
解题思路:
方法一:使用sort排一遍序,如果没有时间复杂度的要求的话,可以OK没问题。
classSolution {
public:vector<int> GetLeastNumbers_Solution(vector<int> input, int k){vector<int> v;if(k>input.size())return v;sort(input.begin(),input.end());for(int i=0;i<k;i++)v.push_back(input[i]);return v; }
};
方法二:使用快排的思想,通过函数计算,使k以前的数都小于k,k之后的数都大于k,这样,最终只需要取前k个数即可。时间复杂度o(n)。
#include<iostream>#include<vector>usingnamespace std;
inteach_sort(vector<int>&a,int i,int j){int tmp=a[i];if(i<j){while(i<j&&a[j]>tmp) j--;if(i<j) a[i]=a[j];while(i<j&&a[i]<tmp) i++;if(i<j) a[j]=a[i];}a[i]=tmp;return i;
}
voidkp_sort(vector<int>&Array,int Begin,int End){if(Begin<End){int tmp=each_sort(Array,Begin,End); //查找每次分配完成的中点kp_sort(Array,Begin,tmp-1); //左边kp_sort(Array,tmp+1,End); //右边}
}
intmain(){vector<int>arr{1,3,2,4,6,5,7,9,13,12};int k;cin>>k;kp_sort(arr,0,arr.size()-1);for(int j=0;j<k;j++)cout<<arr[j]<<',';return0;
}
快排java实现:
classSolution {publicint[] getLeastNumbers(int[] arr, int k) {randomizedSelected(arr, 0, arr.length - 1, k);int[] vec = newint[k];for (inti=0; i < k; ++i) {vec[i] = arr[i];}return vec;}privatevoidrandomizedSelected(int[] arr, int l, int r, int k) {if (l >= r) {return;}intpos= randomizedPartition(arr, l, r);intnum= pos - l + 1;if (k == num) {return;} elseif (k < num) {randomizedSelected(arr, l, pos - 1, k);} else {randomizedSelected(arr, pos + 1, r, k - num);}}// 基于随机的划分privateintrandomizedPartition(int[] nums, int l, int r) {inti=newRandom().nextInt(r - l + 1) + l;swap(nums, r, i);return partition(nums, l, r);}privateintpartition(int[] nums, int l, int r) {intpivot= nums[r];inti= l - 1;for (intj= l; j <= r - 1; ++j) {if (nums[j] <= pivot) {i = i + 1;swap(nums, i, j);}}swap(nums, i + 1, r);return i + 1;}privatevoidswap(int[] nums, int i, int j) {inttemp= nums[i];nums[i] = nums[j];nums[j] = temp;}
}
三、剑指 Offer II 032. 有效的变位词
思路:排序
classSolution {publicbooleanisAnagram(String s, String t) {if(s.length()!=t.length()||s.equals(t)){returnfalse;}char[] a=s.toCharArray();char[] b=t.toCharArray();Arrays.sort(a);Arrays.sort(b);return Arrays.equals(a,b);}
}
相关文章:

排序
一、数据流中的中位数题目描述:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。…...
Android DataStore Proto存储接入流程详解与使用
一、介绍 通过前面的文字,我们已掌握了DataStore 的存储,但是留下一个尾巴,那就是Proto的接入。 Proto是什么? Protobuf,类似于json和xml,是一种序列化结构数据机制,可以用于数据通讯等场景&a…...

HiEV洞察 | 卖一台亏半台,激光雷达第一股禾赛隐忧仍在
作者 | 感知君Alex 编辑 | 王博2月9日晚,禾赛在万众瞩目下登陆纳斯达克,发行价19美元每股,首日涨超11%,市值超过Luminar,登顶全球市值最高的激光雷达公司。 随后两个交易日,其股价均有不同程度的涨幅&#…...
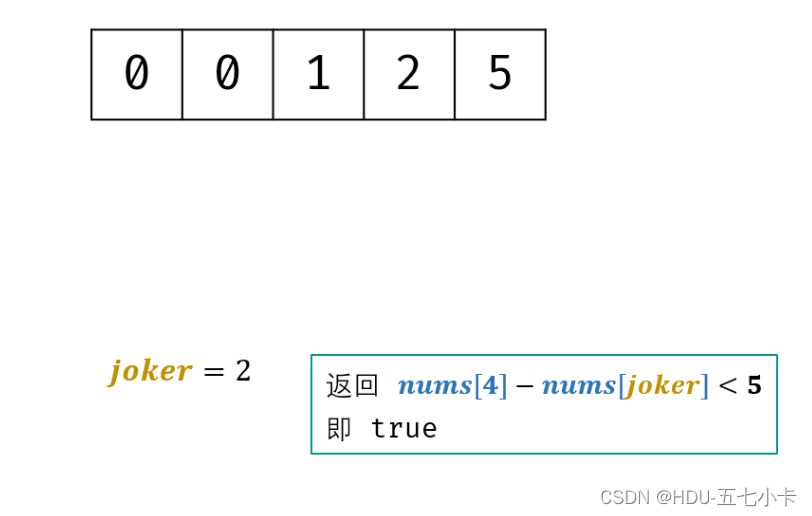
面试题61. 扑克牌中的顺子
题目 从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视…...
有特别有创意的网站设计案例
有人说 UI 设计师集艺术性与科学性于一身,不仅需要对工具的使用熟练,更需要对美术艺术有一定的基础了解。如果想要成为优秀的 UI 设计师是一个需要磨砺的过程,需要不断的学习和积累,多看多练多感受,其中对于优质的设计…...

Python基础-数据类型之列表
一、列表的定义 name ["小明", "小红", "笑笑"] 二、列表的使用 除了序列中的操作,列表还有一些其他的操作。 (1)不使用列表方法对列表进行修改 1:通过索引修改列表中的值 name ["Kit…...
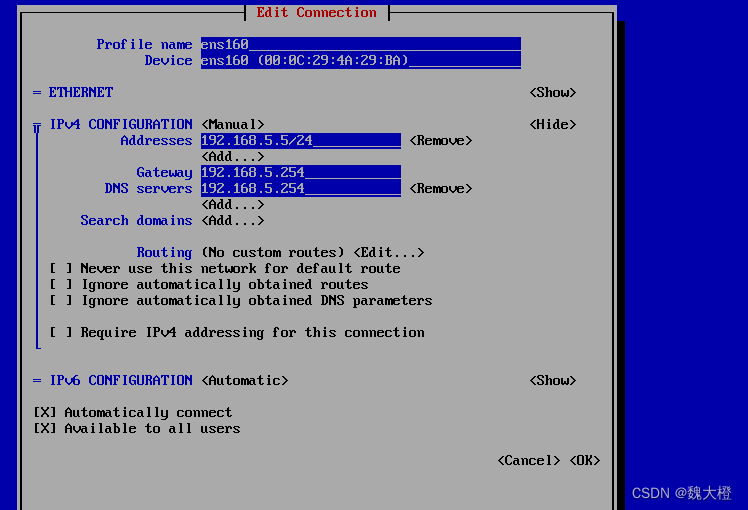
Linux系统基本设置:网络设置(三种界面网络地址配置)
网络地址配置:图形界面配置、命令行界面配置、文本图形界面配置 命令行界面配置 查看网络命令: 想要知道你有多少网卡,都可以通过这两个命令来查看 手动设置网络参数,我们可以使用nmcli这个命令来设置,我们需要知道…...
:查询性能分析)
MySQL(二):查询性能分析
文章目录一、使用explain进行分析二、如何优化数据的访问三、如何重构大查询一、使用explain进行分析 Explain 用来分析 SELECT 查询语句,开发人员可以通过分析 Explain 结果来优化查询语句。 比较重要的字段有: select_type : 查询类型,有…...
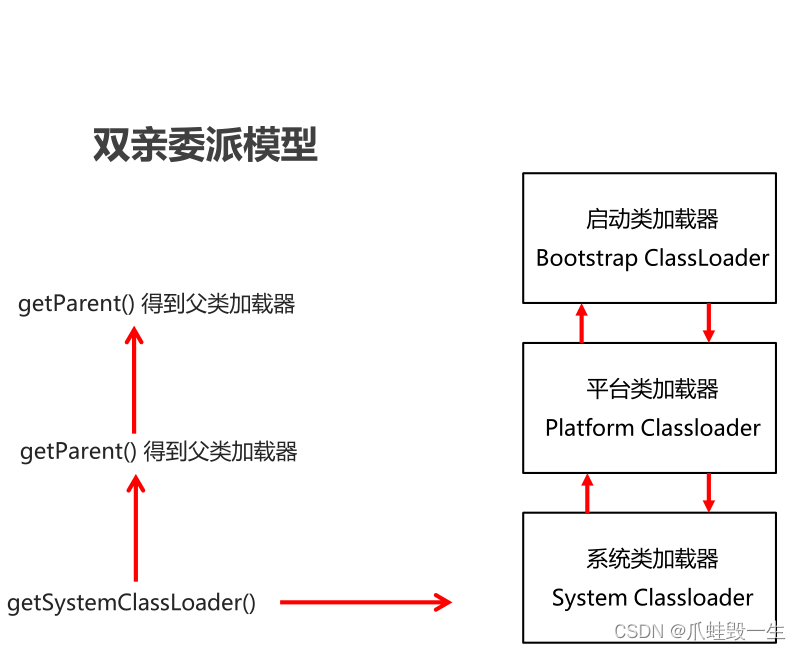
Java基础-类加载器
写在前面的话: 基础加强包含了: 反射,动态代理,类加载器,xml,注解,日志,单元测试等知识点 其中最难的是反射和动态代理,其他知识点都非常简单 由于B站P数限制,…...
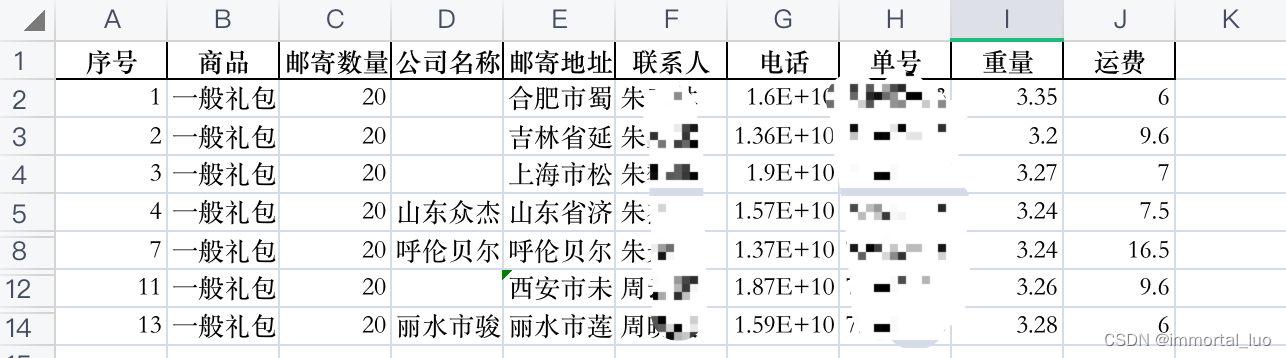
Python 使用pandas处理Excel —— 快递订单处理 数据匹配 邮费计算
问题背景 有表A,其数据如下 关键信息是邮寄地址和单号。 表B: 关键信息是运单号和重量 我们需要做的是,对于表A中的每一条数据,根据其单号,在表B中查找到对应的重量。 在表A中新增一列重量,将刚才查到的…...
【黑马SpringCloud(7)】分布式事务
分布式事务事务的ACID原则分布式事务理论基础CAP定理BASE理论Seataseata的部署seata的集成事务模式XA模式Seata的XA模型优缺点实现XA模式AT模式案例:AT模式更新数据脏写问题优缺点实现AT模式TCC模式流程分析Seata的TCC模型事务悬挂和空回滚实现TCC模式优缺点SAGA模式…...
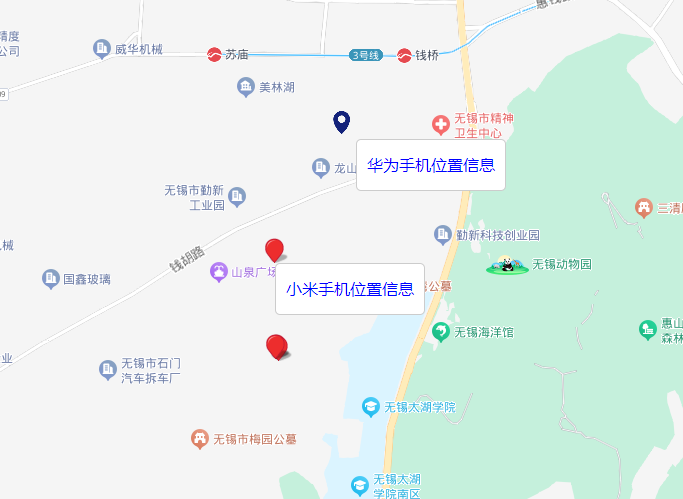
百度地图API添加自定义标记解决单html文件跨域
百度地图API添加自定义标记解决单html文件跨域 因为要往百度地图上添加一些标注点,而且这些标注点要用自定义的图片,而且只能使用单html文件,不能使用服务器(也别问为什么,就是这么个需求),做起…...

如何停止/重启/启动Redis服务
一、命令行直接启动/停止/重启redis 可以直接通过下面的命令启动/停止/重启redis /etc/init.d/redis-server start 启动redis服务 /etc/init.d/redis-server stop 停止redis服务 /etc/init.d/redis-server restart 重启redis服务1、启动redis服务…...
python 的selenium自动操控浏览器教程(2)
人生苦短,我用py 文章目录人生苦短,我用py关于部分网页无法找到元素的问题1方案1方案2关于部分网页无法找到元素的问题2解决方案被网站检查出来我们使用了selenium了怎么办?如何实现前进后退当使用py删除文件时报禁止访问怎么办怎么使用py实现…...

【Deformable Convolution】可变形卷积记录
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 可变形卷积记录 1. 正文 预印版: Deformable Convolutional Networks v1 Deformable ConvNets v2: More Deformable, Better Results 发表版…...

Oracle-Mysql 函数转换
Oracle-Mysql 函数转换limit <> ROWNUMcast <> TO_NUMBERcast as signedcast as unsignedregexp a_\\d <> REGEXP_LIKEschema() <> SELECT USER FROM DUALinformation_schema.COLUMNS表 <> ALL_TAB_COLUMNS表unix_timestampfrom_unixtime <&g…...
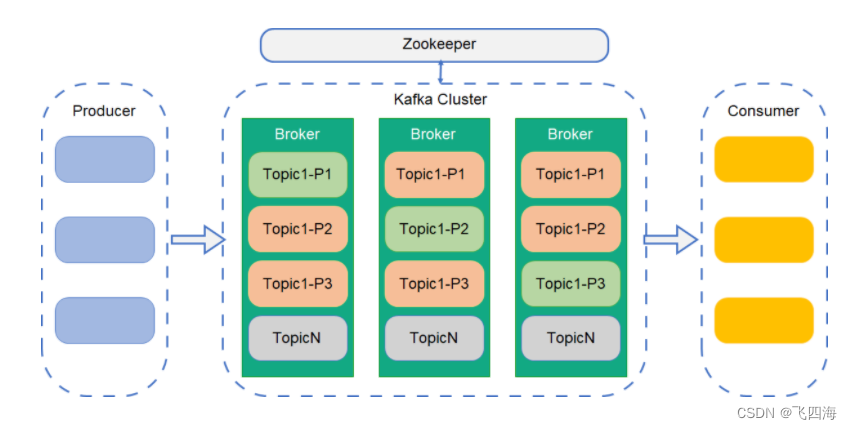
【Kafka】一.认识Kafka
kafka是一个分布式消息队列。由 Scala 开发的高性能跨语言分布式消息队列,单机吞吐量可以到达 10w 级,消息延迟在 ms 级。具有高性能、持久化、多副本备份、横向扩展能力。 生产者往队列里写消息,消费者从队列里取消息进行业务逻辑。 一般在…...

Linux软件管理YUM
目录 yum配置文件 创建仓库 yum查询功能 yum安装与升级功能 yum删除功能 yum仓库产生的问题和解决之道 yum与dnf 网络源 YUM就是通过分析RPM的标头数据后,根据各软件的相关性制作出属性依赖时的解决方案,然后可以自动处理软件的依赖属性问题&…...
【自学MYSQL】MySQL Windows安装
MySQL Windows安装 MySQL Windows下载 首先,我们打开 MySQL 的官网,网址如下: https://dev.mysql.com/downloads/mysql/在官网的主页,我们首先根据我们的操作系统,选择对应的系统,这里我们选择 Windows&…...

Linux c编程之常用技巧
一、说明 在Linux C的实际编程应用中,有很多有用的实践技巧,编程中掌握这些知识,会对编程有事半功倍的效果。 二、常用技巧 2.1 if 变量条件的写法 main.c: #include <stdio.h>int main(int argc, char *argv[]) {int a =...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
