Leetcode.1139 最大的以 1 为边界的正方形
题目链接
Leetcode.1139 最大的以 1 为边界的正方形 Rating : 1744
题目描述
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。
如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
提示:
- 1<=grid.length<=1001 <= grid.length <= 1001<=grid.length<=100
- 1<=grid[0].length<=1001 <= grid[0].length <= 1001<=grid[0].length<=100
grid[i][j]为 0 或 1
分析:
使用 dp 求解,我们定义 f(i,j,0)和f(i,j,1)f(i,j,0)和f(i,j,1)f(i,j,0)和f(i,j,1)分别为以点 (i,j)结尾,向左 和 向上的连续 1的个数。
在f(i,j,0)>0和f(i,j,1)>0f(i,j,0) > 0和f(i,j,1) > 0f(i,j,0)>0和f(i,j,1)>0 的情况下,我们取 d=min(f(i,j,0),f(i,j,1))d = min(f(i,j,0),f(i,j,1))d=min(f(i,j,0),f(i,j,1))。
遍历kkk (0<=k<=d)(0<=k<=d)(0<=k<=d),判断 f(i−k+1,j,0)>=k和f(i,j−k+1,1)>=kf(i-k+1,j,0) >= k 和 f(i,j-k+1,1) >= kf(i−k+1,j,0)>=k和f(i,j−k+1,1)>=k,如果条件成立,说明可以构成一个最后一点是 (i,j),边长为 k的正方形。
时间复杂度:O(m∗n∗min(m∗n))O(m*n*min(m*n))O(m∗n∗min(m∗n))
C++代码:
class Solution {
public:int largest1BorderedSquare(vector<vector<int>>& grid) {int m = grid.size(),n = grid[0].size();int f[m+1][n+1][2];memset(f,0,sizeof f);int ans = 0;for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){//为1就记录if(grid[i-1][j-1]){f[i][j][0] = 1 + (j - 1 >= 1 ? f[i][j-1][0] : 0);f[i][j][1] = 1 + (i - 1 >= 1 ? f[i-1][j][1] : 0);}if(f[i][j][0] > 0 && f[i][j][1] > 0){int d = min(f[i][j][0],f[i][j][1]);//倒序判断能构成正方形的最大边长for(int k = d;k >= 0;k--){if(i-k+1 >= 1 && j-k+1 >= 1 && f[i-k+1][j][0] >= k && f[i][j-k+1][1] >= k){ans = max(ans,k*k);break;}}}}}return ans;}
};
Java代码:
class Solution {public int largest1BorderedSquare(int[][] grid) {int m = grid.length,n = grid[0].length;int[][][] f = new int[m+1][n+1][2];int ans = 0;for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){if(grid[i-1][j-1]==1){f[i][j][0] = 1 + (j - 1 >= 1 ? f[i][j-1][0] : 0);f[i][j][1] = 1 + (i - 1 >= 1 ? f[i-1][j][1] : 0);}if(f[i][j][0] > 0 && f[i][j][1] > 0){int d = Math.min(f[i][j][0],f[i][j][1]);for(int k = d;k >= 0;k--){if(i-k+1 >= 1 && j-k+1 >= 1 && f[i-k+1][j][0] >= k && f[i][j-k+1][1] >= k){ans = Math.max(ans,k*k);break;}}}}}return ans;}
}
相关文章:

Leetcode.1139 最大的以 1 为边界的正方形
题目链接 Leetcode.1139 最大的以 1 为边界的正方形 Rating : 1744 题目描述 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。 如果不存在,则返回 0。…...

Bing+ChatGPT 对传统搜索引擎的降维打击
早些时候申请了新版 Bing 的内测资格,终于收到了通过的邮件。 一天的体验之后,我的感受是:当新版 Bing 具备了 ChatGPT 的聊天能力之后,它的能力不论是对传统搜索引擎,还是 ChatGPT 自身,都将是降维打击。 …...
【JS】数组常用方法总结-功能、参数、返回值
数组常用方法总结-功能、参数、返回值 用简单的js示例 运行在线工具:链接: 菜鸟工具 菜鸟工具示意图: pu…...

pytest 单元测试前后置处理
文章目录方法1 setup/teardown方法2 fixture 夹具方法3 conftest.py测试用例执行前后的一些处理动作,也叫夹具。以下介绍使用前后置操作的几种方法。方法1 setup/teardown setup,每个测试用例执行前要进行的处理。 teardown,每个测试用例执行…...
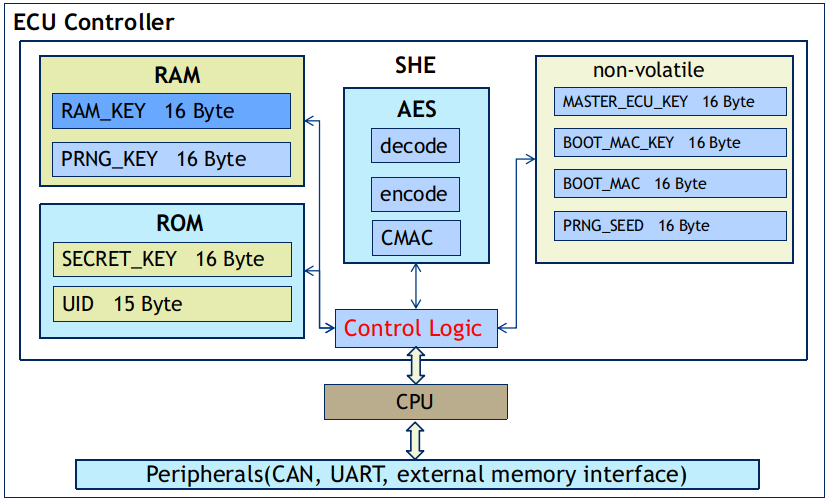
汽车安全硬件扩展 AUTOSAR SHE SecureHardwareExtensions
SHE(Secure Hardware Extension)在车联网中,被应用在车端ECU中负责安全存储与安全计算。是由HIS(由Audi、BMW、Porsche、Volkswagen组成)制定的标准,中文意思“安全硬件扩展”,是对任何给定微控…...
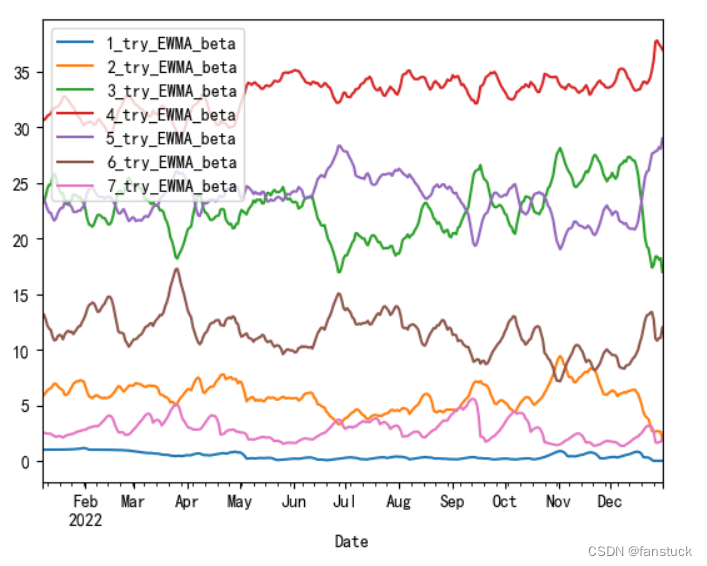
2023年美国大学生数学建模C题:预测Wordle结果建模详解+模型代码
目录 前言 一、题目理解 背景 解析 字段含义: 建模要求 二、建模思路 灰色预测: 编辑 二次指数平滑法: person相关性 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后…...

5、HAL库驱动W25Qxx
一、 SPI通信驱动W25Qxx 1、使用驱动文件快速配置工程代码驱动W25Qxx (此驱动文件只适合W25Qxx 16M及以下型号,因为访问地址位数不同) 注:本次使用SPI的方式进行访问W25Qxx Flash进行数据读写,关于W25Qxx芯片不会做…...
)
git rebase 洐合(变基)
洐合 把一个分支整合到另一个分支的办法有两种:merge(合并) 和 rebase(衍合) 为什么使用? 使提交记录更简洁 三种情况 第一种: 合并多条commit记录 git rebase -i HEAD~合并数量 HEAD~3&a…...

Kubernetes 1.18学习笔记
文章目录一、Kubernetes 概述和架构1、kubernetes 基本介绍2、Kubernetes 功能3、Kubernetes 架构组件4、Kubernetes 核心概念5、Kubernetes 工作原理二、Kubernetes 集群搭建1、系统环境准备1.1 安装要求1.2 系统初始化2、客户端工具kubeadm搭建2.1 安装步骤2.2 安装组件2.3 集…...

AJAX技术
AJAX技术 浏览器是多进程的,简单的说就是,浏览器每打开一个标签页,就相当于创建了一个独立的浏览器进程。但是js是基于单线程的,而这个线程就是浏览器的js引擎,浏览器无论在什么时候都只且只有一个线程在运行JavaScri…...
)
华为OD机试 - 最大排列(JS)
最大排列 题目 给定一组整数,重排序后输出一个最大的整数 输入 数字组合 输出 最大的整数 示例一 输入 10 9输出 910解题思路 我们可以读入一个字符串,将字符串中的单词按照每个单词的字典序长度,字典序从大到小的顺序排序&#x…...
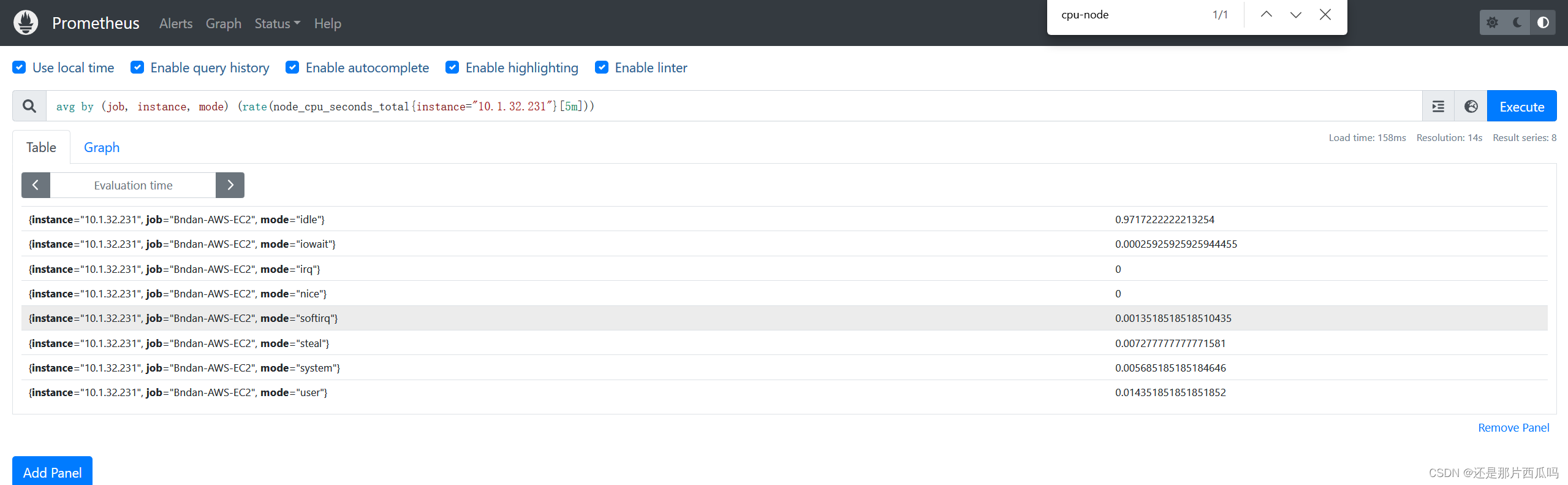
Prometheus Docker安装及监控自身
前提环境: Docker环境 涉及参考文档: 安装Prometheus开始 Prometheusnode_exporter Agent组件 一、部署Prometheus 1、启动容器将文件拷贝出来 docker run -d prom/prometheus2、容器将文件拷贝出来 docker cp 容器ID:/usr/share/prometheus/conso…...

点云处理PCL常用函数与工具
点云处理PCL常用函数与工具 文章目录点云处理PCL常用函数与工具前言一、点云读取与保存数据读取数据保存自定义的点云保存格式二、点云显示点云显示-根据颜色点云显示-根据指定轴数值点云显示-根据指定信息显示多组点云显示三、点云滤波直通滤波统计滤波均匀下采样滤波VoxelGri…...
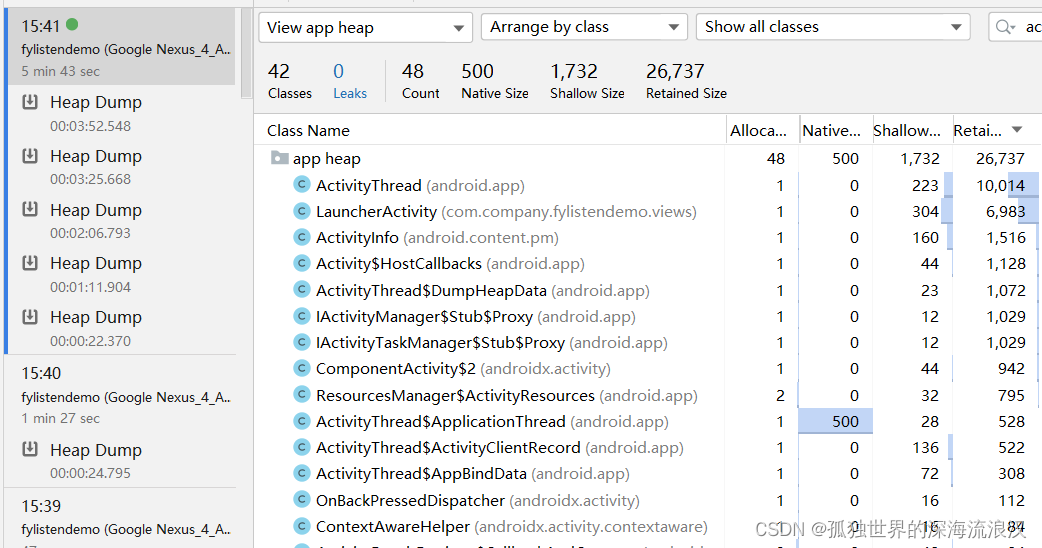
FyListen 在 MVP 架构中的内存优化表现
FyListen 在 MVP 中的内存优化表现 本文只是分享个人开源框架的内存优化测试,你可以直接跳到最后,参考内存泄漏的分析过程! 项目地址: https://github.com/StudyNoteOfTu/fylisten2-alpha1 由于使用到 AOP,所以直接…...
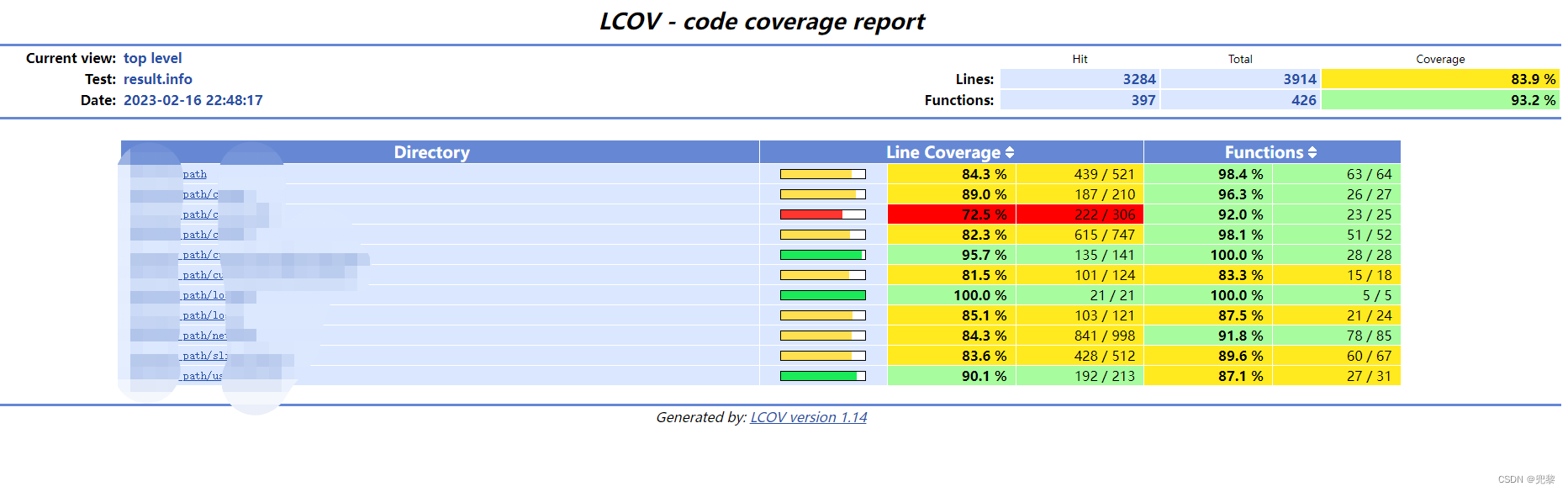
Qt代码单元测试以及报告生成
简介 单元测试是所有测试中最底层的一类测试,是第一个环节,也是最重要的一个环节,是唯一一次有保证能够代码覆盖率达到100%的测试,是整个软件测试过程的基础和前提,单元测试防止了开发的后期因bug过多而失控࿰…...

vscode构建Vue3.0项目(vite,vue-cli)
构建Vue3.0项目构建Vue3.0项目1.使用Vite构建vue项目的方法以及步骤1. 安装vite2. 运行vite vue 项目3.说明2.使用vue-cli构建vue项目的方法以及步骤1.安装全局vue cli —— 脚手架2、VSCode3.报错4.运行构建Vue3.0项目 1.使用Vite构建vue项目的方法以及步骤 1. 安装vite n…...

【2023】华为OD机试真题Java-题目0215-优雅数组
优雅数组 题目描述 如果一个数组中出现次数最多的元素出现大于等于 k k k 次,被称为k-优雅数组, k k k 也可以被称为优雅阈值。 例如,数组[1, 2, 3, 1, 2, 3, 1],它是一个3-优雅数组,因为元素1出现次数大于等于3次...

通过Prowork每日自动提醒待处理工作任务
对于中小团队来说,由于不需要繁琐的流程和高频的异地沟通,需要一款更适合中小团队的日程和项目管理工具。而Prowork就是这样一款敏捷高效的协同平台。Prowork与以往各种项目管理⼯具最⼤的不同在于,其弱化流程和弱化权限的特性,不…...

Linux自定义系统服务
文章目录一. Linux系统服务二. 自定义系统服务一. Linux系统服务 Linux 系统服务有时也称为守护程序,是在Linux启动时自动加载并在Linux退出时自动停止的系统任务,CentOS 7.x开始,CentOS开始使用 systemd服务来代替 daemon ,原来…...

mongodb lambda 查询插件
需求背景需要一个像mybatis plus 一样的基于lambda, 且面向对象的查询mongo数据的插件。在网上找了很久,没有发现有类似功能的插件。于是自己手写了一个,借助mongoTemplate屏蔽了底层查询语句的实现细节。在此基础上,实现了查询的统一封装。技…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
