LeetCode——1237. 找出给定方程的正整数解
一、题目
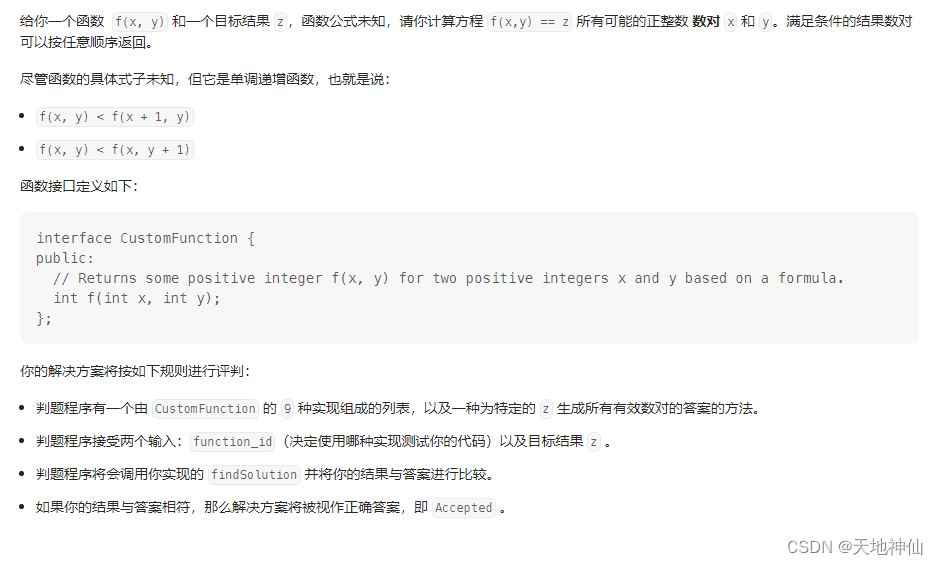

来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/
翻译一下题目
意思是,这是一个二维单调递增的函数,函数一共有 9 种,我们可以直接调用 CustomFunction 这个类来使用他定义的函数。测试用例中输入的 function_id 不在我们的考虑范围内,这个 function_id 只是决定了他具体是采用了哪一种函数来进行运算。而我们要做的事情就是,找到所有满足函数等于 target 的数值对。另外建议出题人下次好好学学语文再来出题吧。
二、C++解法
我的思路及代码
枚举
因为他给出了数据的范围,所有我们可以枚举出所有的情况,然后和 target 进行比较,一样则加入答案。
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;for(int i=1;i<1000;i++){for(int j=1;j<1000;j++){if(z==customfunction.f(i,j)){ans.push_back({i,j});}}}return ans;}
};
- 时间复杂度:O(mn),其中 m 是 x 的取值数目,n 是 y 的取值数目
- 空间复杂度:O(1)
枚举改进
在枚举的基础上增加了提前退出循环的条件,由于该函数是单调递增,所以当 f(x,y) = target 时,f(x,y+1) > target 是一定的,所以我们可以减少很多不必要的循环。除此之外我们还可以进行改进,可以继续往下看
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;for(int i=1;i<1000;i++){for(int j=1;j<1000;j++){if(z==customfunction.f(i,j)){ans.push_back({i,j});}if(z<customfunction.f(i,j))break;}}return ans;}
};
- 时间复杂度:O(mn),其中 m 是 x 的取值数目,n 是 y 的取值数目
- 空间复杂度:O(1)
双指针
由于此函数单调递增,所以我们可以采用双指针,一个遍历 x 的从前往后遍历,另外一个遍历 y 的从后往前遍历,当遇到当前的函数值小于 target 时就说明此时在 x 不变的情况下,y 已经小了,所以我们将 x++ 然后还是从上次遍历停止的位置继续开始 y 的遍历。这样可以大幅度减少搜索的次数。
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;int j=1000;for(int i=1;i<1001;i++){ for(;j>0;j--){if(z==customfunction.f(i,j))ans.push_back({i,j});if(z>customfunction.f(i,j))break;}}return ans;}
};
- 时间复杂度:O(m+n),其中 m 是 x 的取值数目,n 是 y 的取值数目
- 空间复杂度:O(1)
官方参考代码
二分查找
题目本质是一个查找的题目,所以可以用二分查找的办法将时间复杂度降低到 nlogn 的级别
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x++) {int yleft = 1, yright = 1000;while (yleft <= yright) {int ymiddle = (yleft + yright) / 2;if (customfunction.f(x, ymiddle) == z) {res.push_back({x, ymiddle});break;}if (customfunction.f(x, ymiddle) > z) {yright = ymiddle - 1;} else {yleft = ymiddle + 1;}}}return res;}
};
- 时间复杂度:O(mlogn),其中 m 是 x 的取值数目,n 是 y 的取值数目。
- 空间复杂度:O(1)
相关文章:

LeetCode——1237. 找出给定方程的正整数解
一、题目 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 翻译一下题目 意思是,这是一个二维单调递增的函数,函数一共有 9 …...

系统编程中的进程的概念No.3【进程状态】
引言: 北京时间:2023/2/17/8:17,目前听着超能陆战队主题曲《Immortals》,感觉又要螺旋式升天,并且为我今天上午没课感到happy,所以继我们很久以前的关于进程的博客,今天我们就再来学习一下有关…...

推荐 3 款 Golang 语义化版本库
文章目录1.什么是语义化版本 2.0.02.Golang 语义化版本库比较3.小结参考文献1.什么是语义化版本 2.0.0 语义化版本 2.0.0(Semantic Versioning 2.0.0)是一种用于标识软件版本的约定和规范。它包含三个数字组成的版本号,格式为“MAJOR.MINOR.…...
Windows平台使用gdb连接qemu虚拟机上的系统
先安装MinGW; 除了gcc、g,把gdb也选上;可能选第一个就可以了,不清楚把后面几个也选上; 安装完成看一下gcc, g,gdb,编译工具和调试器都有了; 把bin目录加到环境变量; 看一…...
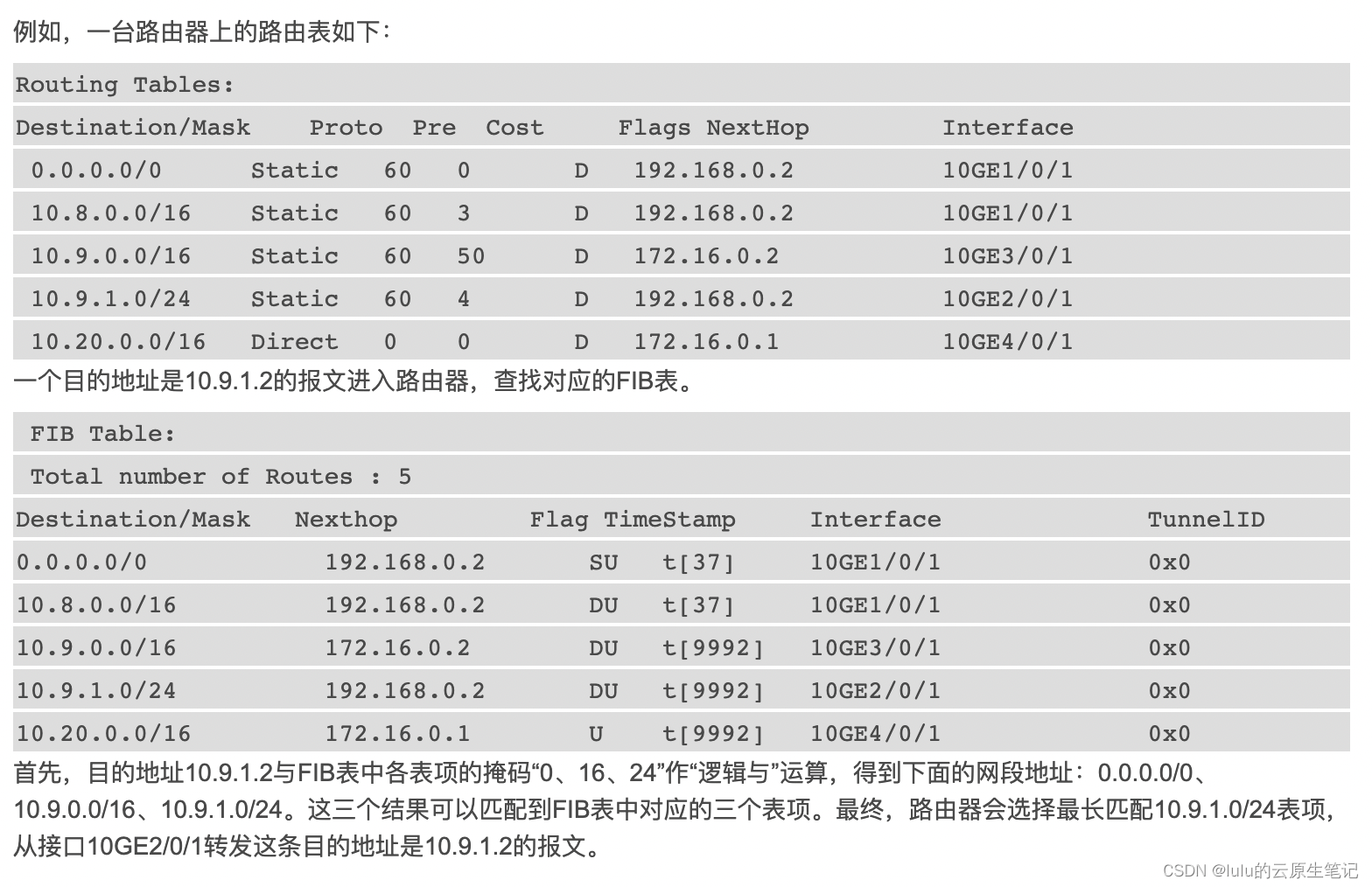
【博客624】MAC地址表、ARP表、路由表(RIB表)、转发表(FIB表)
MAC地址表、ARP表、路由表(RIB表/FIB表) MAC地址表 MAC地址表是交换机等网络设备记录MAC地址和端口的映射关系,代表了交换机从哪个端口学习到了某个MAC地址,交换机把这个信息记录下来,后续交换机需要转发数据的时候就可以根据报文的目的MAC地…...

【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组❆答案解析
【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析 文章目录【蓝桥日记⑤】2014第五届省赛(软件类)JavaA组☃答案解析1、猜年龄2、李白打酒3、神奇算式4、写日志5、锦标赛6、六角填数7、绳圈8、兰顿蚂蚁9、斐波那契10、波动…...

Leetcode.1139 最大的以 1 为边界的正方形
题目链接 Leetcode.1139 最大的以 1 为边界的正方形 Rating : 1744 题目描述 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。 如果不存在,则返回 0。…...

Bing+ChatGPT 对传统搜索引擎的降维打击
早些时候申请了新版 Bing 的内测资格,终于收到了通过的邮件。 一天的体验之后,我的感受是:当新版 Bing 具备了 ChatGPT 的聊天能力之后,它的能力不论是对传统搜索引擎,还是 ChatGPT 自身,都将是降维打击。 …...
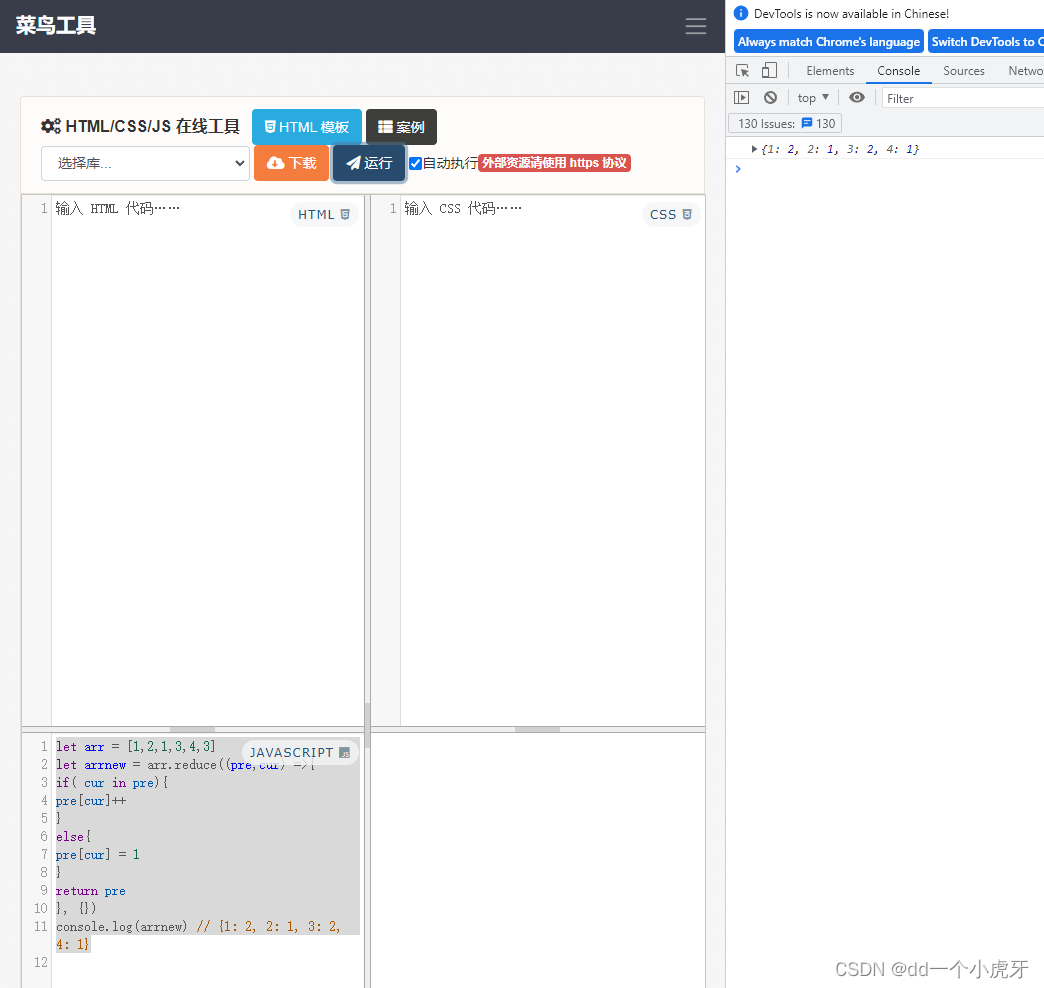
【JS】数组常用方法总结-功能、参数、返回值
数组常用方法总结-功能、参数、返回值 用简单的js示例 运行在线工具:链接: 菜鸟工具 菜鸟工具示意图: pu…...

pytest 单元测试前后置处理
文章目录方法1 setup/teardown方法2 fixture 夹具方法3 conftest.py测试用例执行前后的一些处理动作,也叫夹具。以下介绍使用前后置操作的几种方法。方法1 setup/teardown setup,每个测试用例执行前要进行的处理。 teardown,每个测试用例执行…...
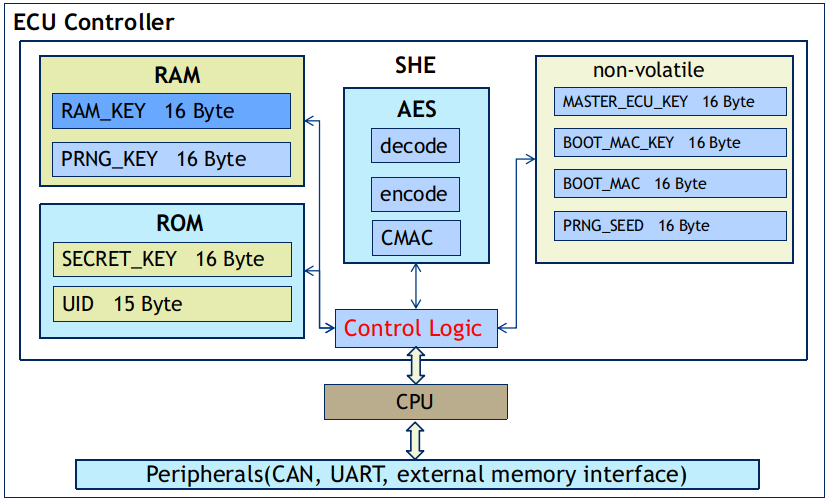
汽车安全硬件扩展 AUTOSAR SHE SecureHardwareExtensions
SHE(Secure Hardware Extension)在车联网中,被应用在车端ECU中负责安全存储与安全计算。是由HIS(由Audi、BMW、Porsche、Volkswagen组成)制定的标准,中文意思“安全硬件扩展”,是对任何给定微控…...
2023年美国大学生数学建模C题:预测Wordle结果建模详解+模型代码
目录 前言 一、题目理解 背景 解析 字段含义: 建模要求 二、建模思路 灰色预测: 编辑 二次指数平滑法: person相关性 只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,以后…...

5、HAL库驱动W25Qxx
一、 SPI通信驱动W25Qxx 1、使用驱动文件快速配置工程代码驱动W25Qxx (此驱动文件只适合W25Qxx 16M及以下型号,因为访问地址位数不同) 注:本次使用SPI的方式进行访问W25Qxx Flash进行数据读写,关于W25Qxx芯片不会做…...
)
git rebase 洐合(变基)
洐合 把一个分支整合到另一个分支的办法有两种:merge(合并) 和 rebase(衍合) 为什么使用? 使提交记录更简洁 三种情况 第一种: 合并多条commit记录 git rebase -i HEAD~合并数量 HEAD~3&a…...

Kubernetes 1.18学习笔记
文章目录一、Kubernetes 概述和架构1、kubernetes 基本介绍2、Kubernetes 功能3、Kubernetes 架构组件4、Kubernetes 核心概念5、Kubernetes 工作原理二、Kubernetes 集群搭建1、系统环境准备1.1 安装要求1.2 系统初始化2、客户端工具kubeadm搭建2.1 安装步骤2.2 安装组件2.3 集…...

AJAX技术
AJAX技术 浏览器是多进程的,简单的说就是,浏览器每打开一个标签页,就相当于创建了一个独立的浏览器进程。但是js是基于单线程的,而这个线程就是浏览器的js引擎,浏览器无论在什么时候都只且只有一个线程在运行JavaScri…...
)
华为OD机试 - 最大排列(JS)
最大排列 题目 给定一组整数,重排序后输出一个最大的整数 输入 数字组合 输出 最大的整数 示例一 输入 10 9输出 910解题思路 我们可以读入一个字符串,将字符串中的单词按照每个单词的字典序长度,字典序从大到小的顺序排序&#x…...
Prometheus Docker安装及监控自身
前提环境: Docker环境 涉及参考文档: 安装Prometheus开始 Prometheusnode_exporter Agent组件 一、部署Prometheus 1、启动容器将文件拷贝出来 docker run -d prom/prometheus2、容器将文件拷贝出来 docker cp 容器ID:/usr/share/prometheus/conso…...

点云处理PCL常用函数与工具
点云处理PCL常用函数与工具 文章目录点云处理PCL常用函数与工具前言一、点云读取与保存数据读取数据保存自定义的点云保存格式二、点云显示点云显示-根据颜色点云显示-根据指定轴数值点云显示-根据指定信息显示多组点云显示三、点云滤波直通滤波统计滤波均匀下采样滤波VoxelGri…...
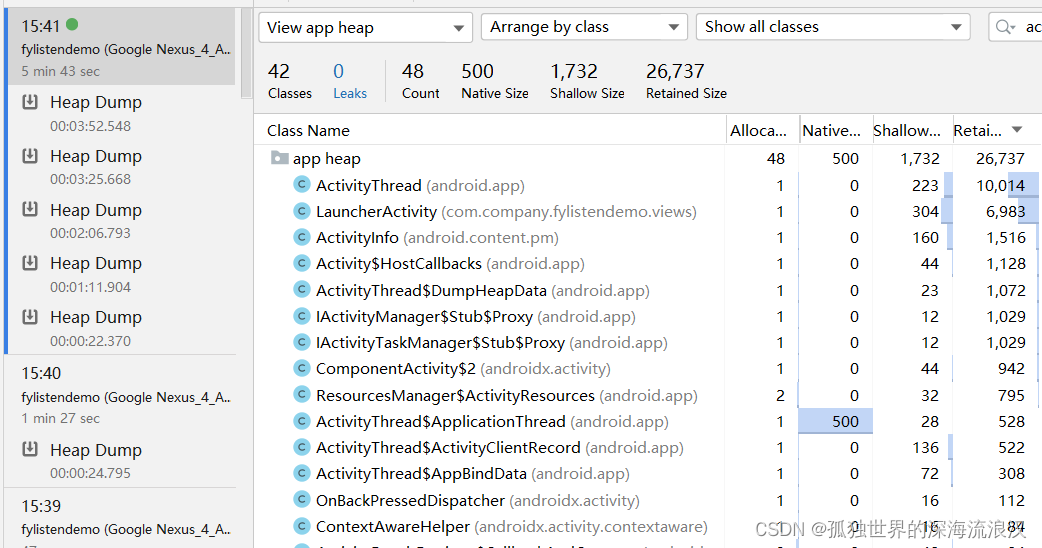
FyListen 在 MVP 架构中的内存优化表现
FyListen 在 MVP 中的内存优化表现 本文只是分享个人开源框架的内存优化测试,你可以直接跳到最后,参考内存泄漏的分析过程! 项目地址: https://github.com/StudyNoteOfTu/fylisten2-alpha1 由于使用到 AOP,所以直接…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
