半导体存储电路
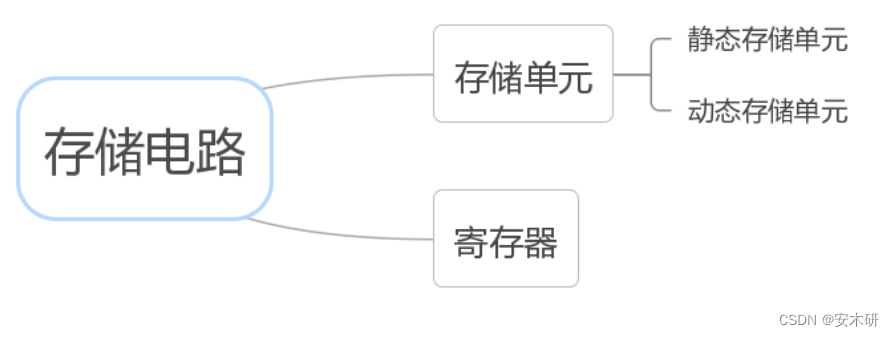
存储电路
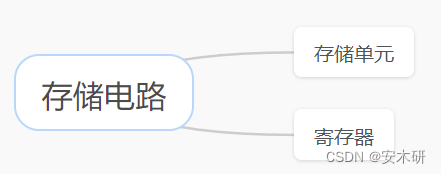
存储单元:只能存储一位数据
寄存器:存储一组数据
存储单元
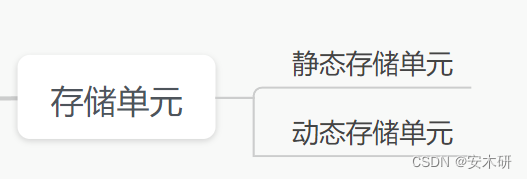
静态存储单元:包含锁存器和触发器,只要不断电,静态存储单元的状态会一直保持下去。
动态存储单元:利用电容的电荷存储效应来存储数据。速度低于静态存储单元,且存在泄露。
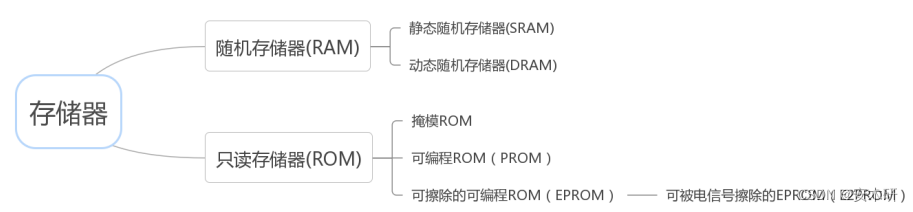
存储器
随机存储器(Random Access Memory):可以随时从其中快速的读出或写入数据
只读存储器(Read-Only Memory):在正常的读写工作状态下,只能从其中读出数据
随机存储器

静态随机存储器(Static Random Access Memory):采用静态存储单元
动态随机存储器(Dynamic Random Access Memory):采用动态存储单元
只读存储器

掩模ROM(Mask Read-Only Memory):不可对其进行更改。
可编程ROM(Programmable Read-Only Memory):可以根据用户需要写入,但写入后不可更改。
可擦除的可编程ROM(Erasable Programmable Read-Only Memory):可以重复写入和更改。
可被电信号擦除的EPROM(Electrically Erasable Programmable Read-Only Memory):U盘和其他便携存储设备用的就是一种E2PROM,也就是“闪存”(Flash Memory)。
SR锁存器
静态存储单元中最基本、也是电路中最简单的一种。
通常由两个 或非门 或者 与非门组成
或非门组成
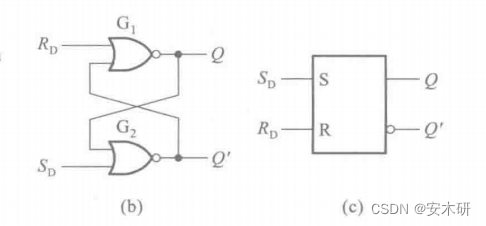
状态分析

真值表
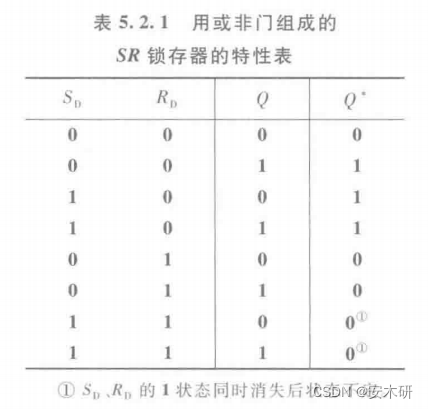
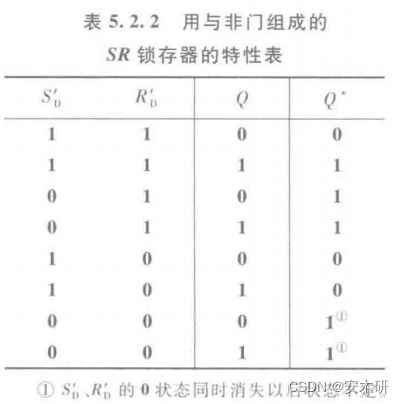
与非门组成
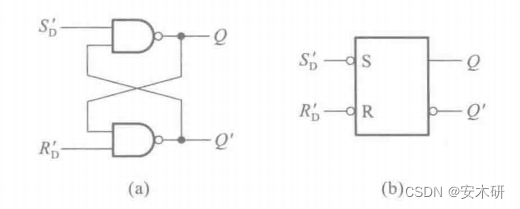
真值表
触发器
触发器比锁存器多了一个触发信号输入端。只有当触发信号来到时,触发器才会置1、0。
这个触发信号称为 时钟(CLOCK),记为CLK。
当有多个触发器需要同时动作时,就可以加一个时钟信号作为 同步控制信号。
工作方式
电平触发、边沿触发、脉冲触发
电平触发
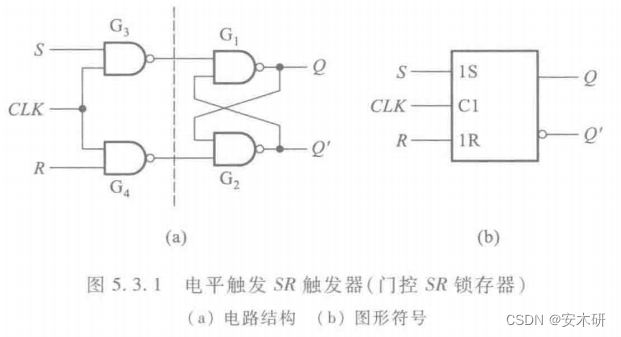
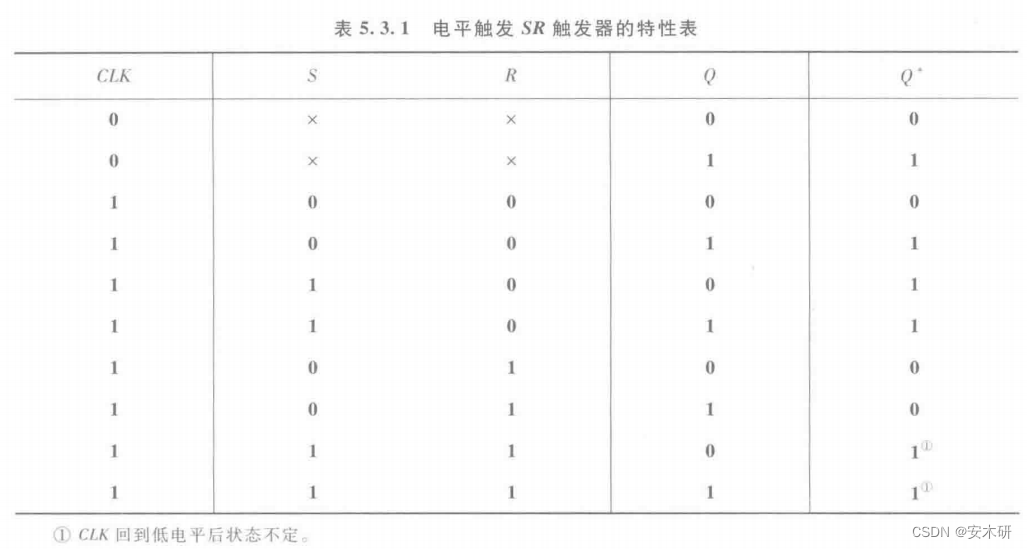
状态分析

真值表
单端信号输入
D触发器
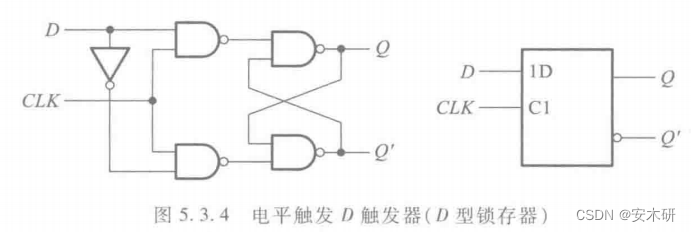
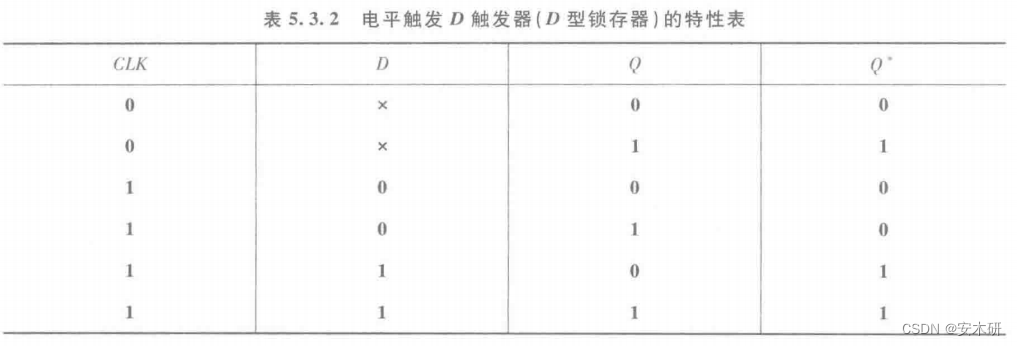
边沿触发
输入信号的状态 在 CLK信号的下降沿(或上升沿)被确定并输出,与边沿变化之前和之后没有关系。
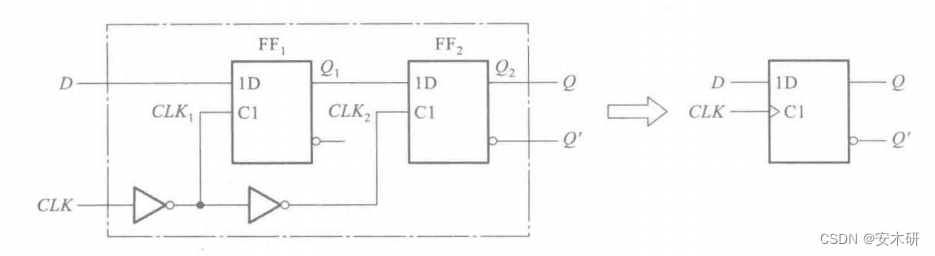
当 CLK 为低的时候,第一个D触发器的时钟为 高,输出信号不确定,可以被改变,
由于此时第二个D触发器的时钟为 低,无法获取第一个D触发器的输出。
当CLK 变为高的时候,第一个D触发器的时钟为 低,输出被确定,并输入到第二个D触发器,
此时第二个D触发器的时钟为 高,获取第一个D触发器的输出并输出。
特性表
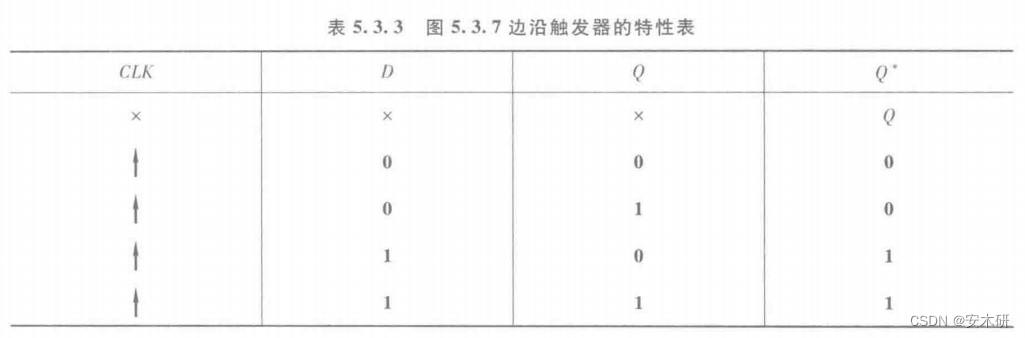
脉冲触发

当时钟为高电平时,第一个触发器的状态可以改变。第二个触发器状态不可以被改变。
当时钟为高电平时,第一个触发器的状态不可以改变。第二个触发器状态可以被改变。
寄存器
由N个触发器组成,通常是把每个触发器的输入端和输出端都直接引出。
存储器
存储器由于引脚数目有限,所以不可能将所有的触发器引脚全部引出,所以给每个存储单元编写了一个地址。
相关文章:

半导体存储电路
存储电路 存储单元:只能存储一位数据 寄存器:存储一组数据 存储单元 静态存储单元:包含锁存器和触发器,只要不断电,静态存储单元的状态会一直保持下去。 动态存储单元:利用电容的电荷存储效应来存储数据。…...

web前端之CSS操作
文章目录 一、CSS操作1.1 html元素的style属性1.2 元素节点的style属性1.3 cssText属性 二、事件2.1 事件处理程序2.1.1 html事件2.1.2 DOM0事件(适合单个事件)2.1.3 DOM2事件(适合多个事件) 2.2 事件之鼠标事件2.3 事件之Event事…...
Python SQLAlchemy ( ORM )
From Python中强大的通用ORM框架:SQLAlchemy:https://zhuanlan.zhihu.com/p/444930067Python ORM之SQLAlchemy全面指南:https://zhuanlan.zhihu.com/p/387078089 SQLAlchemy 文档:https://www.sqlalchemy.org/ SQLAlchemy入门和…...

鉴源实验室丨汽车网络安全运营
作者 | 苏少博 上海控安可信软件创新研究院汽车网络安全组 来源 | 鉴源实验室 社群 | 添加微信号“TICPShanghai”加入“上海控安51fusa安全社区” 01 概 述 1.1 背景 随着车辆技术的不断进步和智能化水平的提升,车辆行业正经历着快速的变革和技术进步。智能化…...

分布式链路追踪之SkyWalking详解和实战
SkyWalking 文章目录 SkyWalking1.SkyWalking概述2.SkyWalking架构设计3.SkyWalking部署4.应用程序接入SkyWalking5.SkyWalking配置应用告警5.1.告警规则5.2.Webhook(网络钩子)5.3.邮件告警实践 6.项目自动化部署接入SkyWalking6.1 整体思路6.2 启动参数…...

【工程实践】使用EDA(Easy Data Augmentation)做数据增强
工程项目中,由于数据量不够,经常需要用到数据增强技术,尝试使用EDA进行数据增强。 1.EDA简介 EDA是一种简单但是非常有效的文本数据增强方法,是由美国Protago实验室发表于 EMNLP-IJCNLP 2019 会议。EDA来自论文《EDA: Easy Data…...

ClickHouse(十三):Clickhouse MergeTree系列表引擎 - ReplicingMergeTree
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

机器学习笔记之优化算法(十)梯度下降法铺垫:总体介绍
机器学习笔记之优化算法——梯度下降法铺垫:总体介绍 引言回顾:线搜索方法线搜索方法的方向 P k \mathcal P_k Pk线搜索方法的步长 α k \alpha_k αk 梯度下降方法整体介绍 引言 从本节开始,将介绍梯度下降法 ( Gradient Descent,GD ) …...

Selenium 根据元素文本内容定位
使用xpath定位元素时,有时候担心元素位置会变,可以考虑使用文本内容来定位的方式。 例如图中的【股市】按钮,只有按钮文本没变,即使位置变化也可以定位到该元素。 xpath内容样例: # 文本内容完全匹配 //button[text(…...

第17章-Spring AOP经典应用场景
文章目录 一、日志处理二、事务控制三、参数校验四、自定义注解五、AOP 方法失效问题1. ApplicationContext2. AopContext3. 注入自身 六、附录1. 示例代码 AOP 提供了一种面向切面操作的扩展机制,通常这些操作是与业务无关的,在实际应用中,可…...

Leetcode周赛 | 2023-8-6
2023-8-6 题1体会我的代码 题2我的超时代码题目体会我的代码 题3体会我的代码 题1 体会 这道题完全就是唬人,只要想明白了,只要有两个连续的数的和,大于target,那么一定可以,两边一次切一个就好了。 我的代码 题2 我…...

ts中interface自定义结构约束和对类的约束
一、interface自定义结构约束对后端接口返回数据 // interface自定义结构 一般用于较复杂的结构数据类型限制 如后端返回的接口数据// 首字母大写;用分割号隔开 interface Iobj{a:number;b:string } let obj:Iobj {a:1,b:2 }// 复杂类型 模拟后端返回的接口数据 interface Il…...

Oracle单实例升级补丁
目录 1.当前DB环境2.下载补丁包和opatch的升级包3.检查OPatch的版本4.检查补丁是否冲突5.关闭数据库实例,关闭监听6.应用patch7.加载变化的SQL到数据库8.ORACLE升级补丁查询 oracle19.3升级补丁到19.18 1.当前DB环境 [oraclelocalhost ~]$ cat /etc/redhat-releas…...

力扣初级算法(二分查找)
力扣初级算法(二分法): 每日一算法:二分法查找 学习内容: 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 2.二分查找流程&…...

探索未来:直播实时美颜SDK在增强现实(AR)直播中的前景
在AR直播中,观众可以与虚拟元素实时互动,为用户带来更加丰富、沉浸式的体验。那么,直播美颜SDK在AR中有哪些应用呢?下文小编将于大家一同探讨美颜SDK与AR有哪些关联。 一、AR直播与直播实时美颜SDK的结合 增强现实技术在直播中…...

SQL 单行子查询 、多行子查询、单行函数、聚合函数 IN 、ANY 、SOME 、ALL
单行子查询 子查询结果是 一个列一行记录 select a,b,c from table where a >(select avg(xx) from table ) 还支持这种写法,这种比较少见 select a,b,c from table where (a ,b)(select xx,xxx from table where col‘000’ )…...
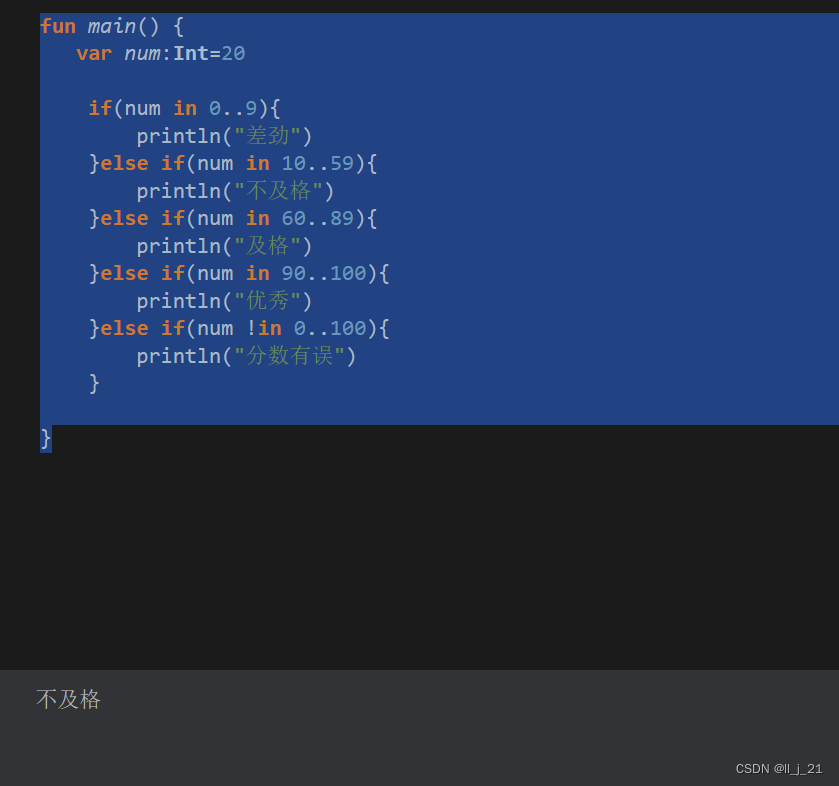
【第一阶段】kotlin的range表达式
range:范围:从哪里到哪里的意思 in:表示在 !in:表示不在 … :表示range表达式 代码示例: fun main() {var num:Int20if(num in 0..9){println("差劲")}else if(num in 10..59){println("不及格")}else if(num in 60..89…...
)
网络防御(5)
一、结合以下问题对当天内容进行总结 1. 什么是恶意软件? 2. 恶意软件有哪些特征? 3. 恶意软件的可分为那几类? 4. 恶意软件的免杀技术有哪些? 5. 反病毒技术有哪些? 6. 反病毒网关的工作原理是什么? 7. 反…...

gradle 命令行单元测试执行问题
文章目录 问题:命令行 执行失败最终解决方案(1)ADB命令(2)Java 环境配置 问题:命令行 执行失败 命令行 执行测试命令 无法使用(之前还能用的。没有任何改动,又不能用了) …...

剑指Offer12.矩阵中的路径 C++
1、题目描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
