38.利用matlab解 有约束无约束的参数估计对比(matlab程序)
1.简述
1.离散型随机变量的极大似然估计法:
(1) 似然函数
若X为离散型, 似然函数为
(2) 求似然函数L(θ)的最大值点 θ, 则θ就是未知参数的极大似然估计值.
2.连续型随机变量的极大似然估计法:
(1) 似然函数
若 X 为连续型, 似然函数为
(2) 求似然函数L(θ)的最大值点θ, 则θ就是未知参数 的极大似然估计值.
一、矩估计
设总体X的均值、方差均存在,样本(X1,X2,……,X n),则不管总体服从什么分布,总体均值的矩估计均为样本均值,方差的矩估计均为样本二阶中心矩。
matlab中提供了下列函数来实现总体均值的矩估计值与方差的矩估计值的计算,如下:
mu_ju=mean(X) % 返回样本X的均值
sigma2_ju =moment(X,2) % 返回样本X的2阶中心矩
例:来自某总体X的样本值如下:
232.50, 232.48, 232.15, 232.52, 232.53, 232.30, 232.48, 232.05, 232.45, 232.60, 232.47, 232.30,求X的均值与方差的矩估计。
>> x=[232.50,232.48,232.15,232.52,232.53,232.30,232.48,232.05,232.45,232.60,232.47,232.30]
mu_ju=mean(x)
sigma2_ju= moment(x,2)
x =
232.5000 232.4800 232.1500 232.5200 232.5300 232.3000 232.4800 232.0500 232.4500 232.6000 232.4700 232.3000
mu_ju =
232.4025
sigma2_ju =
0.0255
二、单个总体极大似然估计与区间估计(参数均未知)
命令: [a,b]=namefit (X, ALPHA) % 返回总体参数的极大似然估计a与置信度为100(1- ALPHA)的置信区间 [a,b],若参数为多个,ab也是多个,若省略ALPHA,则置信度为0.95
下表列出了几种常用分布的参数估计函数:
函数名 调 用 形 式 函 数 说 明
binofit PHAT= binofit(X, N);[PHAT, PCI] = binofit(X,N);[PHAT, PCI]= binofit (X, N, ALPHA) 二项分布的概率的最大似然估计置信度为95%的最大似然估计和置信区间返回水平α的参数估计和置信区间
poissfit Lambdahat=poissfit(X);[Lambdahat, Lambdaci] = poissfit(X);[Lambdahat, Lambdaci]= poissfit (X, ALPHA) 泊松分布的参数的最大似然估计置信度为95%的最大似然估计和置信区间返回水平α的λ参数和置信区间
normfit [muhat,sigmahat,muci,sigmaci] = normfit(X);[muhat,sigmahat,muci,sigmaci] = normfit(X, ALPHA) 正态分布的最大似然估计,置信度为95%返回水平α的期望、方差值和置信区间
betafit PHAT =betafit (X);[PHAT, PCI]= betafit (X, ALPHA) 返回β分布参数a和 b的最大似然估计返回最大似然估计值和水平α的置信区间
unifit [ahat,bhat] = unifit(X);[ahat,bhat,ACI,BCI] = unifit(X);[ahat,bhat,ACI,BCI]=unifit(X, ALPHA) 均匀分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计和置信区间
expfit muhat =expfit(X);[muhat,muci] = expfit(X);[muhat,muci] = expfit(X,alpha) 指数分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计和置信区间
gamfit phat =gamfit(X);[phat,pci] = gamfit(X);[phat,pci] = gamfit(X,alpha) γ分布参数的最大似然估计置信度为95%的参数估计和置信区间返回最大似然估计值和水平α的置信区间
weibfit phat = weibfit(X);[phat,pci] = weibfit(X);[phat,pci] = weibfit(X,alpha) 韦伯分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计及其区间估计
Mle phat = mle(‘dist’,data);[phat,pci] = mle(‘dist’,data);[phat,pci] = mle(‘dist’,data,alpha);[phat,pci] = mle(‘dist’,data,alpha,p1) 分布函数名为dist的最大似然估计置信度为95%的参数估计和置信区间返回水平α的最大似然估计值和置信区间仅用于二项分布,pl为试验总次数
对于上表函数,以均匀分布的参数估计为例说明:
例、产生 100 行1列服从区间(1, 10)上的均匀分布的随机数, 计算区间端点“a”和“b”的极大似然估计值, 求出置信度为0.95的这两个参数的置信区间。
三、单个正态总体参数估计
设X1,X2,……Xn,为来自正态总体N(u,sigma^2)的一个样本,求u,sigma ^2的极大似然估计与区间估计。此处会较多用到数理统计的知识,参见下表。
只需要按照表中所对应的估计函数计算即可。只不过在计算之前,有必要去了解一下matlab中如何去计算某一分布的临界值。
2.代码
function my_ga_fit_nonline()
x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.00 14.00 16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.00 24.00 24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.00 32.00 34.00 36.00 36.00 38.00 38.00 40.00 42.00]';
y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.43 0.44 0.43 0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.40 0.41 0.41 0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.39 0.39]';
A=[];
B=[];
AE=[];
BE=[];
lb =[ ];
ub =[ ];
options=optimset('display','iter','MaxFunEvals',1e3,'MaxIter',1e10,'TolFun',1e-8,'TolX',1e-8);
numberOfVariables = 2;%需拟合参数的个数
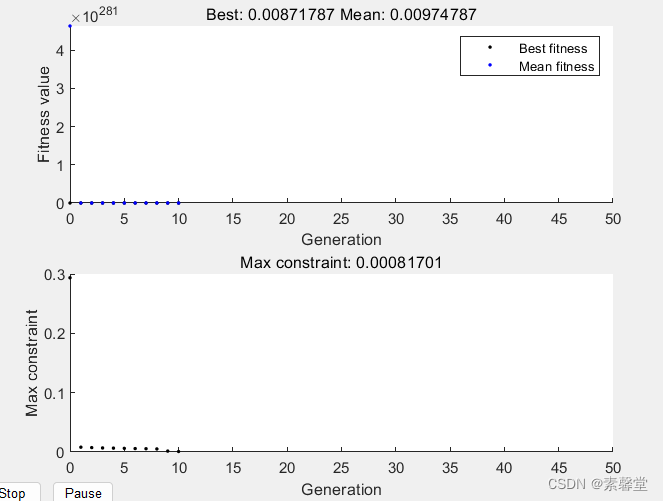
opt= gaoptimset('PlotFcns',{@gaplotbestf,@gaplotmaxconstr},'Display','iter',...
'PopulationSize',50, 'Generations',50,'StallGenLimit',50,'StallTimeLimit',50,'CrossoverFraction',0.85,'MutationFcn',@mutationadaptfeasible);
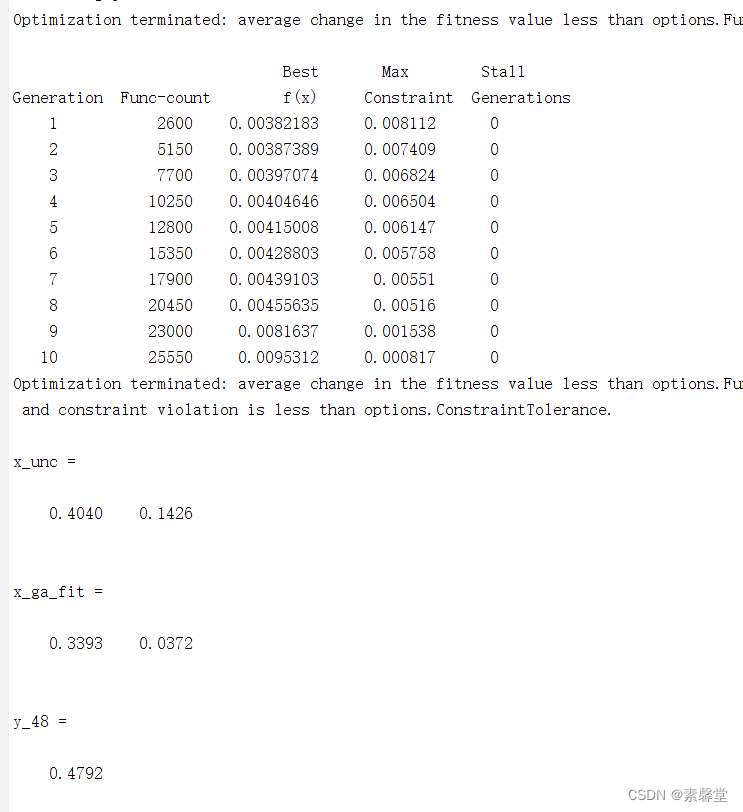
[x_unc, fval_unc, exitflag]=ga(@myfuntest,numberOfVariables,A,B,AE,BE,lb,ub,[]);
[x_ga_fit, fval_error, exitflag]=ga(@myfuntest,numberOfVariables,A,B,AE,BE,lb,ub,@myconfun,opt);
x_unc
x_ga_fit
y_48=(x_ga_fit(1)+(0.49-x_ga_fit(1)).*exp(-x_ga_fit(2).*(10-8)))
y_unc=x_ga_fit(1)+(0.49-x_ga_fit(1)).*exp(-x_ga_fit(2).*(x-8));
yy=x_unc(1)+(0.49-x_unc(1)).*exp(-x_unc(2).*(x-8));
err_unc=sum(abs(y_unc-y))
err=sum(abs(yy-y))
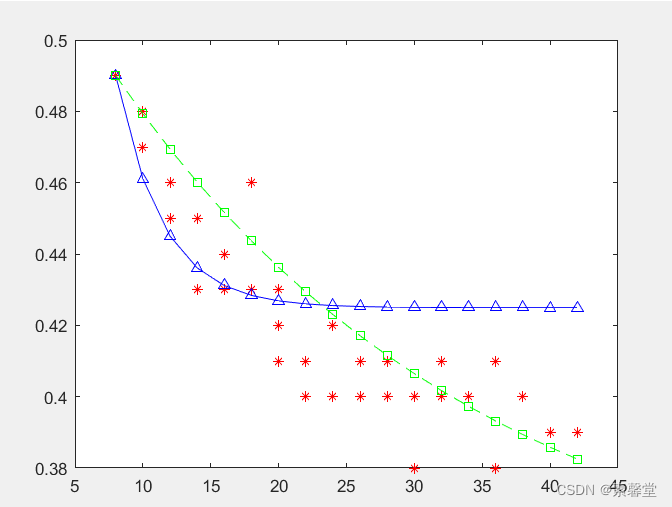
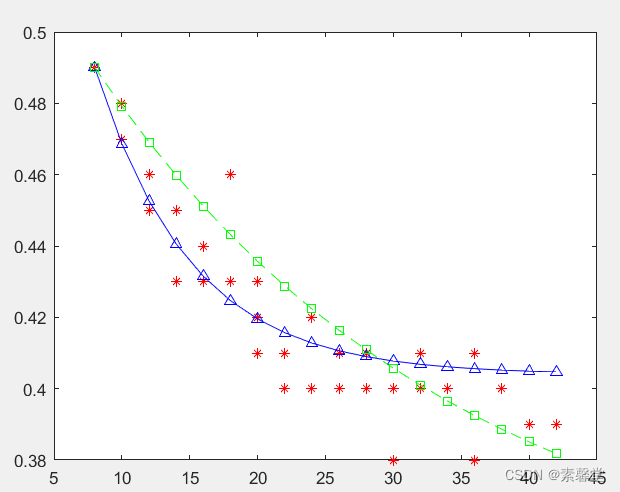
figure
plot(x,y,'r*',x,yy,'b-^',x,y_unc,'--gs')
function f = myfuntest(z)
f=zeros(1,1);
for i=1:length(x)
f=f+((z(1)+(0.49-z(1)).*exp(-z(2).*(x(i)-8))-y(i)).^2);
end
end
function [c, ceq] =myconfun(z)
c=[];
ceq=[(z(1)+(0.49-z(1)).*exp(-z(2).*(10-8))-0.48)];
end
end
3.运行结果

相关文章:

38.利用matlab解 有约束无约束的参数估计对比(matlab程序)
1.简述 1.离散型随机变量的极大似然估计法: (1) 似然函数 若X为离散型, 似然函数为 (2) 求似然函数L(θ)的最大值点 θ, 则θ就是未知参数的极大似然估计值. 2.连续型随机变量的极大似然估计法: (1) 似然函数 若 X 为连续型, 似然函数为 (2) 求似然函数L(θ)的最大值点θ, 则…...
什么是React?React与VU的优缺点有哪些?
什么是React?什么是VUE? 维基百科上的概念解释,Vue.js是一个用于创建用户界面的开源MVVM前端JavaScript框架,也是一个创建单页应用的Web应用框架。Vue.js由尤雨溪(Evan You)创建,由他和其他活跃…...

区块链技术助力慈善,为您的善举赋予全新力量!
我们怀揣着一颗温暖的心,秉承着公开透明的理念,带着信任与责任,倾力打造了一套区块链技术驱动的去中心化捐赠与物资分发系统,通过智能生态网络(IEN)解决捐赠不透明问题的系统,让您的善举直接温暖…...

模拟实现消息队列项目(系列4) -- 服务器模块(内存管理)
目录 前言 1. 创建MemoryDataCenter 2. 封装Exchange 和 Queue方法 3. 封装Binding操作 4. 封装Message操作 4.1 封装消息中心集合messageMap 4.2 封装消息与队列的关系集合queueMessageMap的操作 5. 封装未确认消息集合waitMessage的操作 6. 从硬盘中恢复数据到内存中 7. Memo…...
STM32 LoRa源码解读
目录结构: SX1278 |-- include | |-- fifo.h | |-- lora.h | |-- platform.h | |-- radio.h | |-- spi.h | |-- sx1276.h | |-- sx1276Fsk.h | |-- sx1276FskMisc.h | |-- sx1276Hal.h | |-- sx1276LoRa.h | -- sx1276LoRaMisc.h – src |-- fifo.c |-- lora.c |-- …...
)
【BASH】回顾与知识点梳理(十)
【BASH】回顾与知识点梳理 十 十. 文件的格式化与相关处理10.1 格式化打印: printf10.2 awk:好用的数据处理工具awk 的逻辑运算字符 10.3 文件比对工具diffcmppatch 10.4 文件打印准备: pr 该系列目录 --> 【BASH】回顾与知识点梳理&#…...
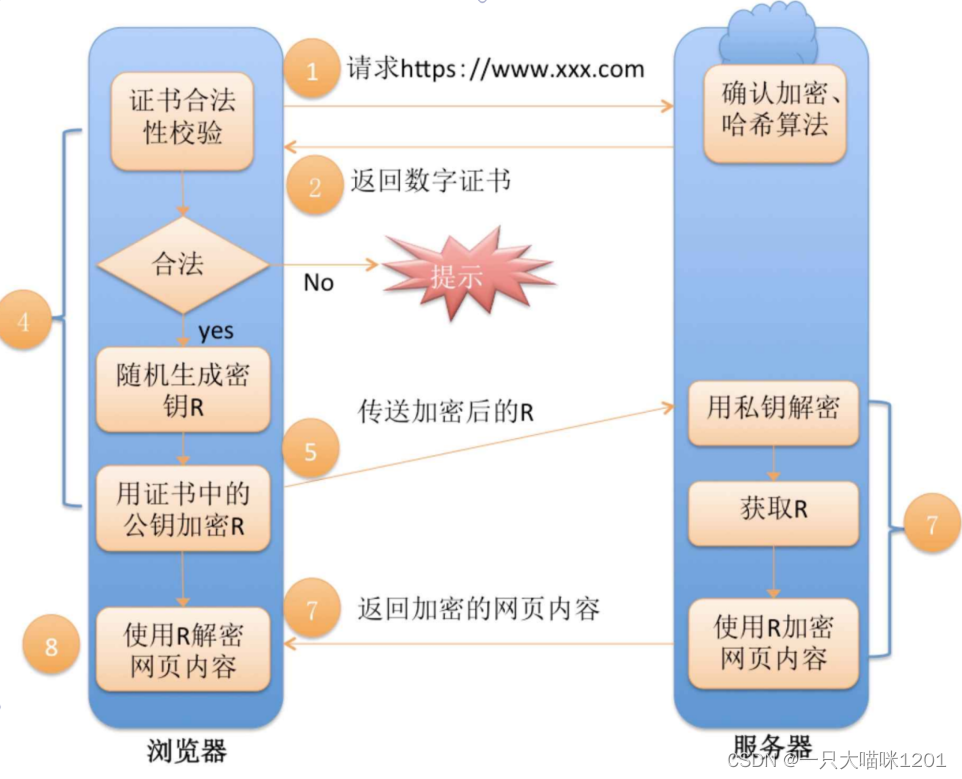
【网络】应用层——HTTPS协议
🐱作者:一只大喵咪1201 🐱专栏:《网络》 🔥格言:你只管努力,剩下的交给时间! HTTPS协议 🍉HTTP的不安全性🍉认识HTTPS协议🍓加密解密ἵ…...
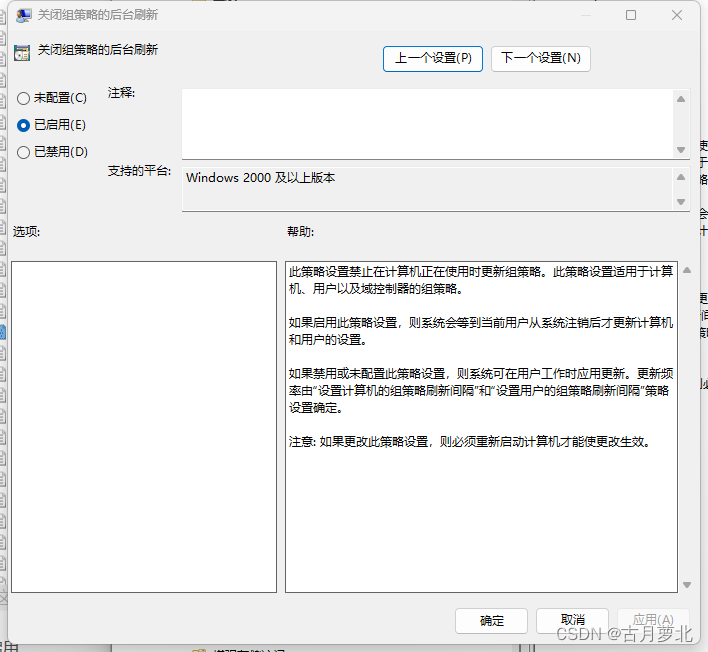
Windows新版文件资源管理器经常在后台弹出的临时解决方案
禁用组策略自动刷新 运行gpedit.msc找到计算机配置->管理模板->系统->组策略找到 “关闭组策略的后台刷新”启用 参考 https://answers.microsoft.com/en-us/windows/forum/all/windows-11-most-recently-opened-explorer-window/26e097bd-1eba-4462-99bd-61597b5…...
软考高项(八)项目整合管理 ★重点集萃★
👑 个人主页 👑 :😜😜😜Fish_Vast😜😜😜 🐝 个人格言 🐝 :🧐🧐🧐说到做到,言出必行&am…...

基于python+django开发的学生信息管理系统
基于pythondjangovue.js开发的学生信息管理系统,师弟的课程作业 功能介绍 平台采用B/S结构,后端采用主流的Python语言进行开发,前端采用主流的Vue.js进行开发。 功能包括:学生管理、班级管理、用户管理、日志管理、系统信息模块…...
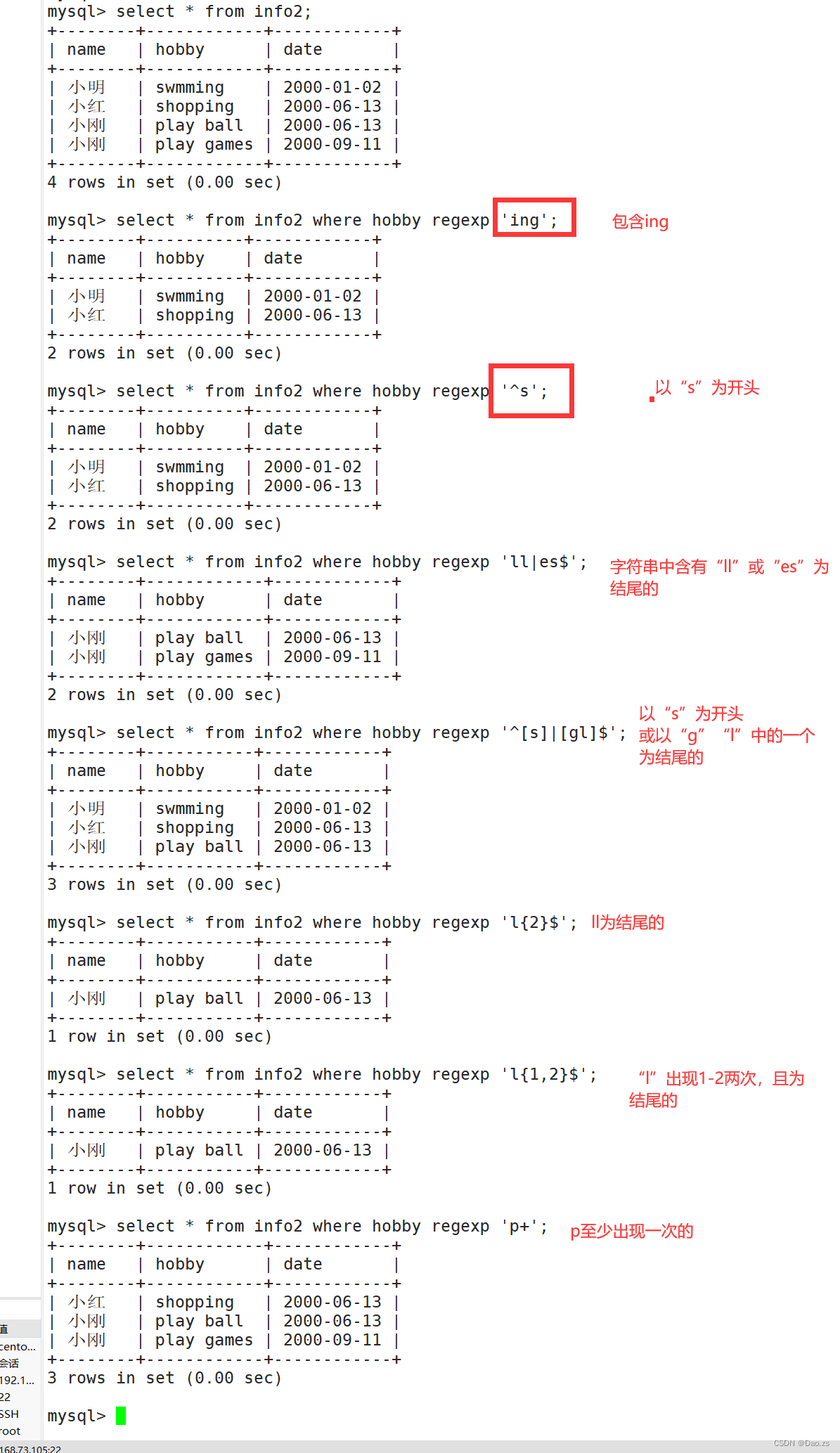
mysql的高级查询语句
目录 一、本文前言 二、高效查询方式 1)指定指字段进行查看 2)对字段进行去重查看 3)where条件查询 4)and 和 or 进行逻辑关系的增加 5)查询取值列表中的数据 6)between的引用 7)like…...
04-8_Qt 5.9 C++开发指南_QTableWidget的使用
文章目录 1. QTableWidget概述2. 源码2.1 可视化UI设计2.2 程序框架2.3 qwintspindelegate.h2.4 qwintspindelegate.cpp2.5 mainwindow.h2.6 mainwindow.cpp 1. QTableWidget概述 QTableWidget是Qt中的表格组件类。在窗体上放置一个QTableWidget 组件后,可以在 PropertyEditor…...

《golang设计模式》第二部分·结构型模式-01-适配器模式(Adapter)
文章目录 1. 概念1.1 角色1.2 应用场景1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 示例类图 1. 概念 定义一个适配器,帮助原本不能实现接口的类“实现”该接口 1.1 角色 目标(Target):客户端调用的目标接口 被适配者(…...

机器学习概述及其主要算法
目录 1、什么是机器学习 2、数据集 2.1、结构 3、算法分类 4、算法简介 4.1、K-近邻算法 4.2、贝叶斯分类 4.3、决策树和随机森林 4.4、逻辑回归 4.5、神经网络 4.6、线性回归 4.7、岭回归 4.8、K-means 5、机器学习开发流程 6、学习框架 1、什么是机器学习 机器…...

识jvm堆栈中一个数据类型是否为为引用类型,目前虚拟机实现中是如何做的?
调用栈里的引用类型数据是GC的根集合(root set)的重要组成部分;找出栈上的引用是GC的根枚举(root enumeration)中不可或缺的一环。 要看JVM选择用什么方式。通常这个选择会影响到GC的实现。 如果JVM选择不记录任何这种…...

Bug合集
这里会收藏后面所遇到的bug并附上具有参考的意义的博客,会持续更新 Java 1、SpringBoot升级2.6.0以上后,Swagger出现版本不兼容报错。 Failed to start bean ‘documentationPluginsBootstrapper‘; nested exception is java.lang.NullPo…...
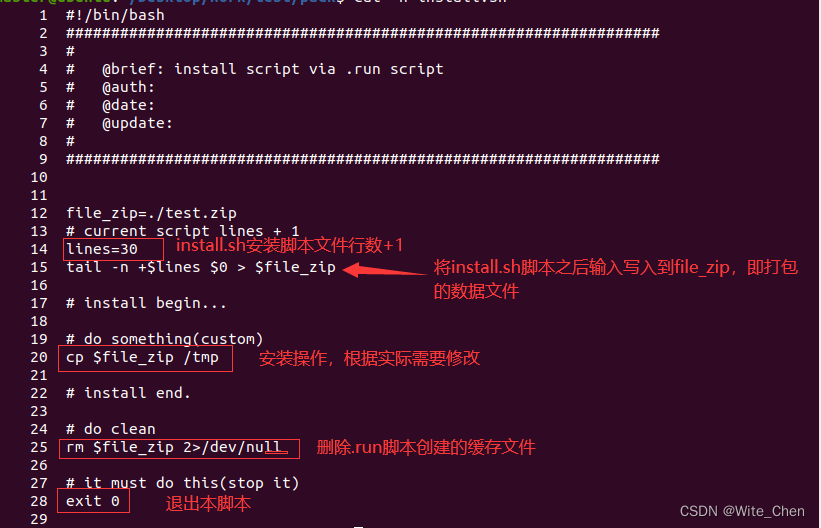
linux下.run安装脚本制作
1、安装文件(install.sh) PS: .run安装包内部执行脚本文件 2、资源文件(test.zip) PS: 待安装程序源文件 3、制作.run脚本(install.run) cat install.sh test.zip > install.run chmod ax install.run...
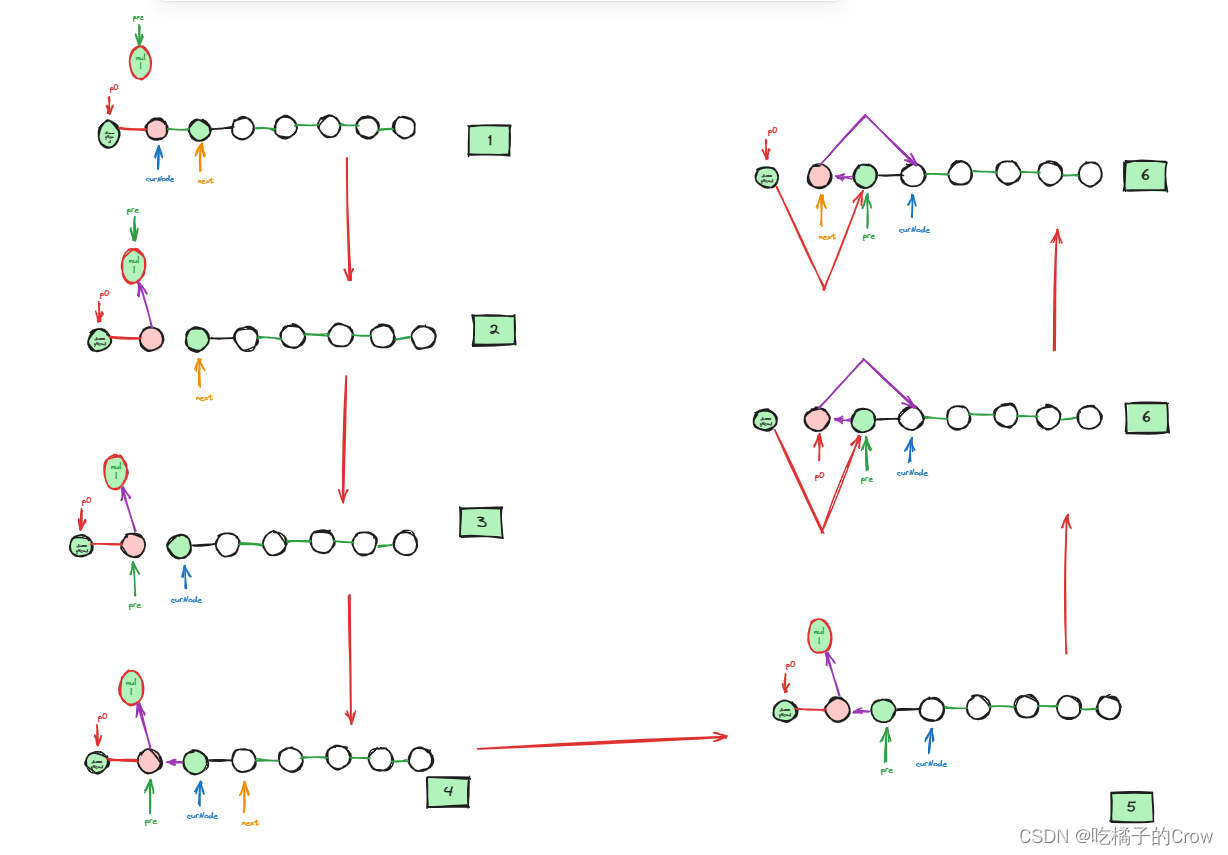
面试热题(翻转k个链表)
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯的改变节点内部的值&a…...
每天10个小知识点)
前端面试的性能优化部分(4)每天10个小知识点
目录 系列文章目录前端面试的性能优化部分(1)每天10个小知识点前端面试的性能优化部分(2)每天10个小知识点前端面试的性能优化部分(3)每天10个小知识点前端面试的性能优化部分(4)每天…...

el-checkbox修改选中和未选中的值
由于在checkbox选中的时候,默认的是为true和false。 后端定义的绑定字段不是为布尔值,而是为0,1 解决办法 <el-checkbox v-model"model.status" :true-label"1" :false-label"0"> </el-checkbox>…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
