2023国赛数学建模思路 - 案例:退火算法
文章目录
- 1 退火算法原理
- 1.1 物理背景
- 1.2 背后的数学模型
- 2 退火算法实现
- 2.1 算法流程
- 2.2算法实现
- 建模资料
## 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 退火算法原理
1.1 物理背景
在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低,物体的能量状态会低;够低后,液体开始冷凝与结晶,在结晶状态时,系统的能量状态最低。大自然在缓慢降温(亦即,退火)时,可“找到”最低能量状态:结晶。但是,如果过程过急过快,快速降温(亦称「淬炼」,quenching)时,会导致不是最低能态的非晶形。
如下图所示,首先(左图)物体处于非晶体状态。我们将固体加温至充分高(中图),再让其徐徐冷却,也就退火(右图)。加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小(此时物体以晶体形态呈现)。
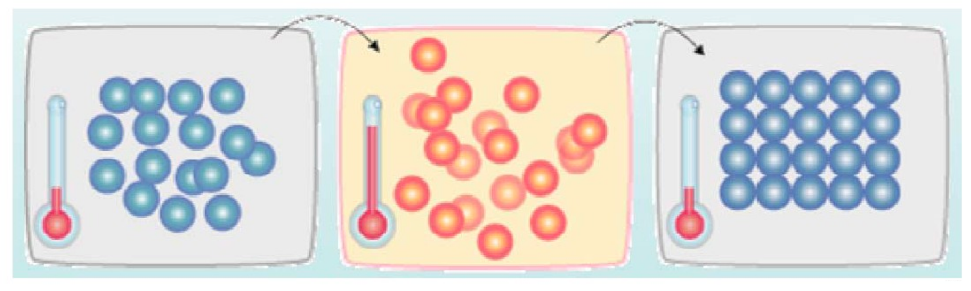
1.2 背后的数学模型
如果你对退火的物理意义还是晕晕的,没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数,现在想求函数的(全局)最优解。如果采用Greedy策略,那么从A点开始试探,如果函数值继续减少,那么试探过程就会继续。而当到达点B时,显然我们的探求过程就结束了(因为无论朝哪个方向努力,结果只会越来越大)。最终我们只能找打一个局部最后解B。
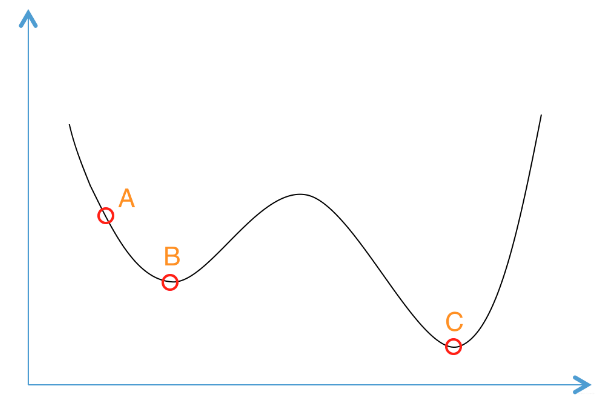
根据Metropolis准则,粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为
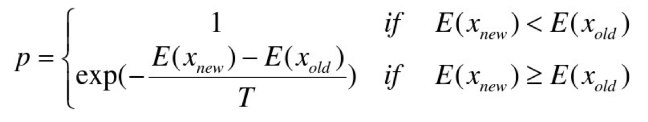
Metropolis准则表明,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:P(dE) = exp( dE/(kT) )。其中k是一个常数,exp表示自然指数,且dE<0。所以P和T正相关。这条公式就表示:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(因为退火的过程是温度逐渐下降的过程),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。也就是说,在用固体退火模拟组合优化问题,将内能E模拟为目标函数值 f,温度T演化成控制参数 t,即得到解组合优化问题的模拟退火演算法:由初始解 i 和控制参数初值 t 开始,对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代,并逐步衰减 t 值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。
2 退火算法实现
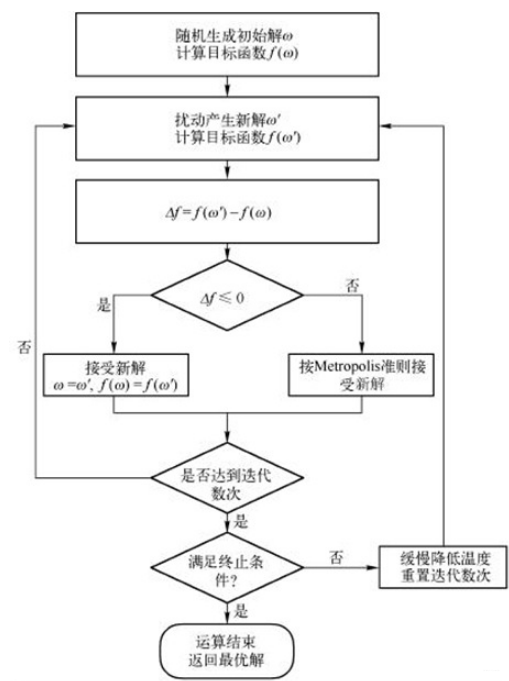
2.1 算法流程
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点), 每个T值的迭代次数L
(2) 对k=1,……,L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数
(5) 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2
2.2算法实现
import numpy as np
import matplotlib.pyplot as plt
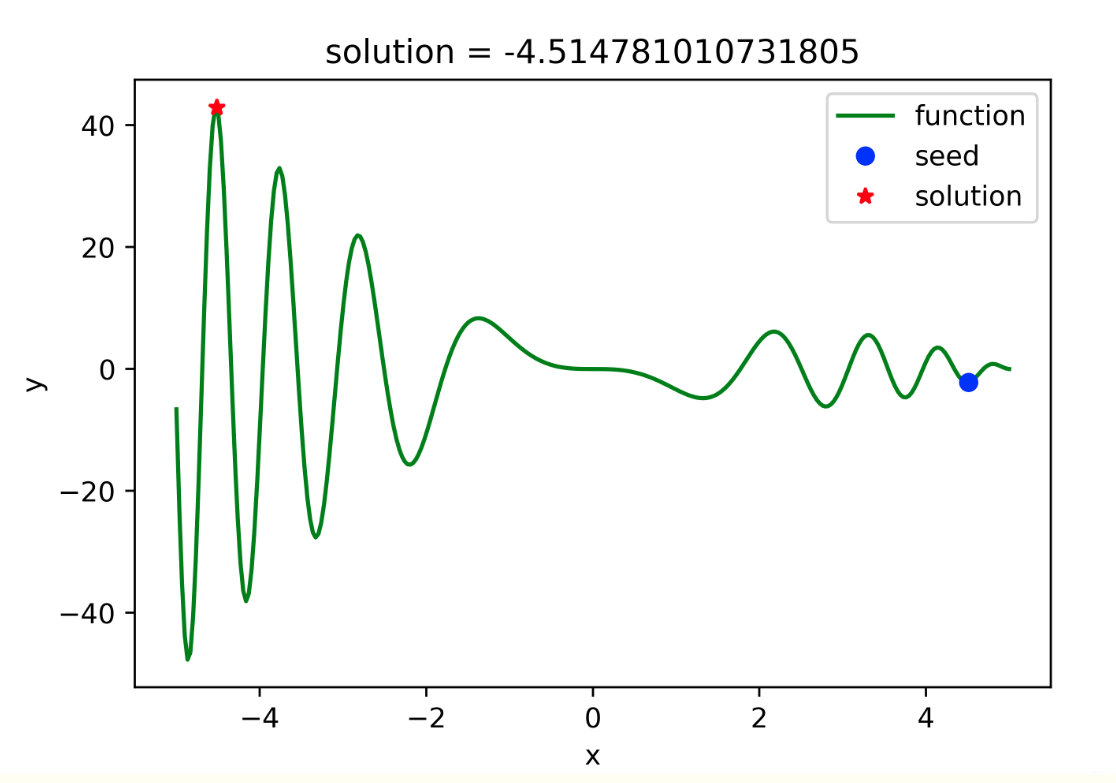
import randomclass SA(object):def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):self.interval = interval # 给定状态空间 - 即待求解空间self.T_max = T_max # 初始退火温度 - 温度上限self.T_min = T_min # 截止退火温度 - 温度下限self.iterMax = iterMax # 定温内部迭代次数self.rate = rate # 退火降温速度#############################################################self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值#############################################################self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def solve(self):temp = 'deal_' + self.tab # 采用反射方法提取对应的函数if hasattr(self, temp):deal = getattr(self, temp)else:exit('>>>tab标签传参有误:"min"|"max"<<<')x1 = self.x_seedT = self.T_maxwhile T >= self.T_min:for i in range(self.iterMax):f1 = self.func(x1)delta_x = random.random() * 2 - 1if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内x2 = x1 + delta_xelse:x2 = x1 - delta_xf2 = self.func(x2)delta_f = f2 - f1x1 = deal(x1, x2, delta_f, T)T *= self.rateself.x_solu = x1 # 提取最终退火解def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率probability = np.exp(-delta/T)return probabilitydef p_max(self, delta, T):probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率return probabilitydef deal_min(self, x1, x2, delta, T):if delta < 0: # 更优解return x2else: # 容忍解P = self.p_min(delta, T)if P > random.random(): return x2else: return x1def deal_max(self, x1, x2, delta, T):if delta > 0: # 更优解return x2else: # 容忍解P = self.p_max(delta, T)if P > random.random(): return x2else: return x1def display(self):print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))plt.figure(figsize=(6, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')plt.title('solution = {}'.format(self.x_solu))plt.xlabel('x')plt.ylabel('y')plt.legend()plt.savefig('SA.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':SA([-5, 5], 'max')
实现结果
建模资料
资料分享: 最强建模资料


相关文章:

2023国赛数学建模思路 - 案例:退火算法
文章目录 1 退火算法原理1.1 物理背景1.2 背后的数学模型 2 退火算法实现2.1 算法流程2.2算法实现 建模资料 ## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上&a…...
ubuntu20.04 编译安装运行emqx
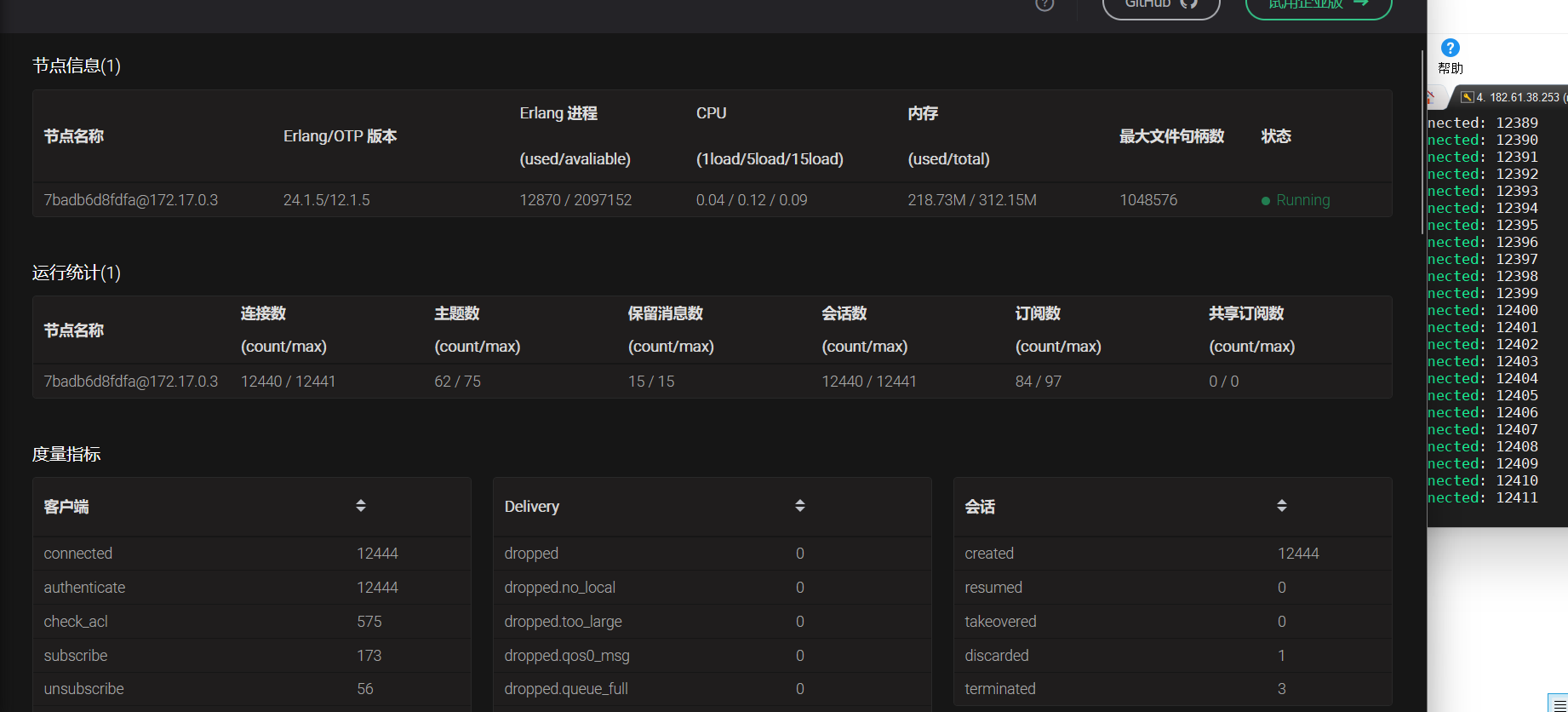
文章目录 安装依赖编译运行登录dashboard压力测试 安装依赖 Erlang/OTP OTP 24 或 25 版本 apt-get install libncurses5-dev sudo apt-get install erlang如果安装的erlang版本小于24的话,可以使用如下方法自行编译erlang 1.源码获取 wget https://github.com/erla…...

ARM linux ALSA 音频驱动开发方法
+他V hezkz17进数字音频系统研究开发交流答疑群(课题组) 一 linux ALSA介绍 ALSA (Advanced Linux Sound Architecture) 是一个用于提供音频功能的开源软件框架。它是Linux操作系统中音频驱动程序和用户空间应用程序之间的接口。ALSA 提供了访问声卡硬件的低级别API,并支持…...
)
设计模式二十三:模板方法模式(Template Method Pattern)
定义了一个算法的框架,将算法的具体步骤延迟到子类中实现。这样可以在不改变算法结构的情况下,允许子类重写算法的特定步骤以满足自己的需求 模版方法使用场景 算法框架固定,但具体步骤可以变化:当你有一个算法的整体结构是固定…...
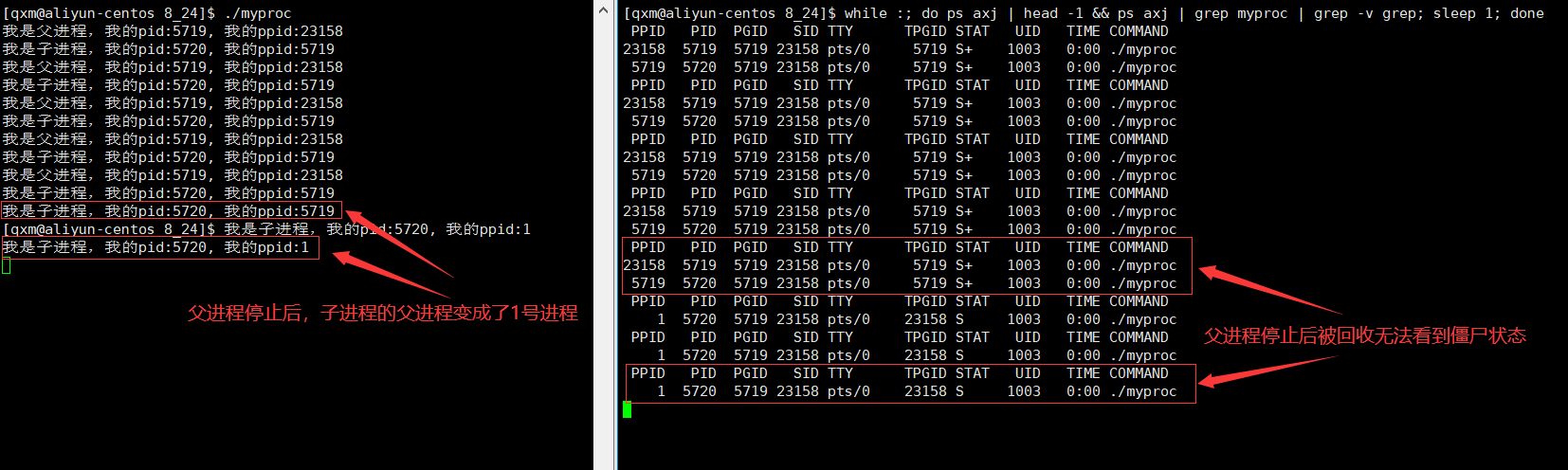
[Linux]进程状态
[Linux]进程状态 文章目录 [Linux]进程状态进程状态的概念阻塞状态挂起状态Linux下的进程状态孤儿进程 进程状态的概念 了解进程状态前,首先要知道一个正在运行的进程不是无时无刻都在CPU上进行运算的,而是在操作系统的管理下,和其他正在运行…...
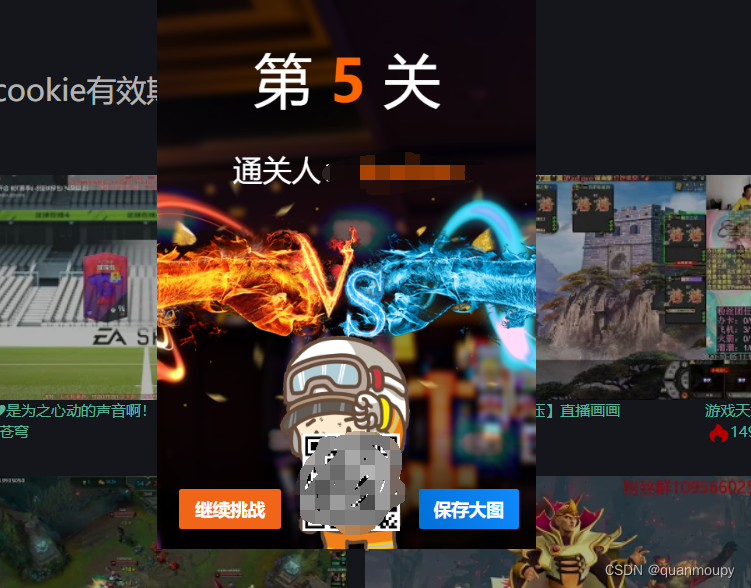
Python爬虫逆向实战案例(五)——YRX竞赛题第五题
题目:抓取全部5页直播间热度,计算前5名直播间热度的加和 地址:https://match.yuanrenxue.cn/match/5 cookie中m值分析 首先打开开发者工具进行抓包分析,从抓到的包来看,参数传递了查询参数m与f,同时页面中…...

js识别图片中的文字插件 tesseract.js
使用方法及步骤 1.安装依赖 npm i tesseract.js 2.引入插件 import { createWorker } from tesseract.js;//worker多线程引入这个import Tesseract from tesseract.js;//js单线程引入这个 3.使用插件识别图片 //使用worker线程识别(async () > {console.time()const wo…...
)
Linux设备驱动移植(设备数)
一、设备数 设备树是一种描述硬件信息的数据结构,Linux内核运行时可以通过设备树将硬件信息直接传递给Linux内核,而不再需要在Linux内核中包含大量的冗余编码 设备数语法概述 设备树文件 dts 设备树源文件 dtsi 类似于头文件,包含一些公共的…...

【移动端开发】鸿蒙系统开发入门:代码示例与详解
一、引言 随着华为鸿蒙系统的日益成熟,越来越多的开发者开始关注这一新兴的操作平台。本文旨在为初学者提供一份详尽的鸿蒙系统开发入门指南,通过具体的代码示例,引导大家逐步掌握鸿蒙开发的基本概念和技术。 二、鸿蒙系统开发基础 鸿蒙系…...

Jenkins的流水线详解
来源:u.kubeinfo.cn/ozoxBB 什么是流水线 声明式流水线 Jenkinsfile 的使用 什么是流水线 jenkins 有 2 种流水线分为声明式流水线与脚本化流水线,脚本化流水线是 jenkins 旧版本使用的流水线脚本,新版本 Jenkins 推荐使用声明式流水线。…...

DIFFEDIT-图像编辑论文解读
文章目录 摘要算法Step1:计算编辑maskStep2:编码Step3:使用mask引导进行解码理论分析: 实验数据集:扩散模型:ImageNet数据集上实验消融实验IMAGEN数据集上实验COCO数据集上实验 结论 论文: 《D…...

【优选算法】—— 字符串匹配算法
在本期的字符串匹配算法中,我将给大家带来常见的两种经典的示例: 1、暴力匹配(BF)算法 2、KMP算法 目录 (一)暴力匹配(BF)算法 1、思想 2、演示 3、代码展示 (二&…...

Docker容器:docker consul的注册与发现及consul-template守护进程
文章目录 一.docker consul的注册与发现介绍1.什么是服务注册与发现2.什么是consul3.docker consul的应用场景4.consul提供的一些关键特性5.数据流向 二.consul部署1.consul服务器(192.168.198.12)(1)建立 Consul 服务启动consul后…...
Blazor 依赖注入妙用:巧设回调
文章目录 前言依赖注入特性需求解决方案示意图 前言 依赖注入我之前写过一篇文章,没看过的可以看看这个。 C# Blazor 学习笔记(10):依赖注入 依赖注入特性 只能Razor组件中注入所有Razor组件在作用域注入的都是同一个依赖。作用域可以看看我之前的文章。 需求 …...
)
Python 基础 -- Tutorial(三)
7、输入和输出 有几种方法可以表示程序的输出;数据可以以人类可读的形式打印出来,或者写入文件以备将来使用。本章将讨论其中的一些可能性。 7.1 更花哨的输出格式 到目前为止,我们已经遇到了两种写值的方法:表达式语句和print()函数。(第三种方法是使…...
基于STM32的四旋翼无人机项目(二):MPU6050姿态解算(含上位机3D姿态显示教学)
前言:本文为手把手教学飞控核心知识点之一的姿态解算——MPU6050 姿态解算(飞控专栏第2篇)。项目中飞行器使用 MPU6050 传感器对飞行器的姿态进行解算(四元数方法),搭配设计的卡尔曼滤波器与一阶低通滤波器…...

微信小程序开发教学系列(1)- 开发入门
第一章:微信小程序简介与入门 1.1 简介 微信小程序是一种基于微信平台的应用程序,可以在微信内直接使用,无需下载和安装。它具有小巧、高效、便捷的特点,可以满足用户在微信中获取信息、使用服务的需求。 微信小程序采用前端技…...
Nginx虚拟主机(server块)部署Vue项目
需求 配置虚拟主机,实现一个Nginx运行多个服务。 实现 使用Server块。不同的端口号,表示不同的服务;同时在配置中指定,Vue安装包所在的位置。 配置 Vue项目,放在 html/test 目录下。 config中的配置如下…...

JAVA开发环境接口swagger-ui使用总结
一、前言 swagger-ui是java开发中生产api说明文档的插件,这是后端工程师和前端工程师联调接口的桥梁。生成的文档就减少了很多没必要的沟通提高开发和测试效率。 二、 swagger-ui的使用 1、引入maven依赖 <dependency><groupId>io.springfox</grou…...

mongodb 数据库管理(数据库、集合、文档)
目录 一、数据库操作 1、创建数据库 2、删除数据库 二、集合操作 1、创建集合 2、删除集合 三、文档操作 1、创建文档 2、 插入文档 3、查看文档 4、更新文档 1)update() 方法 2)replace() 方法 一、数据库操作 1、创建数据库 创建数据库…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
