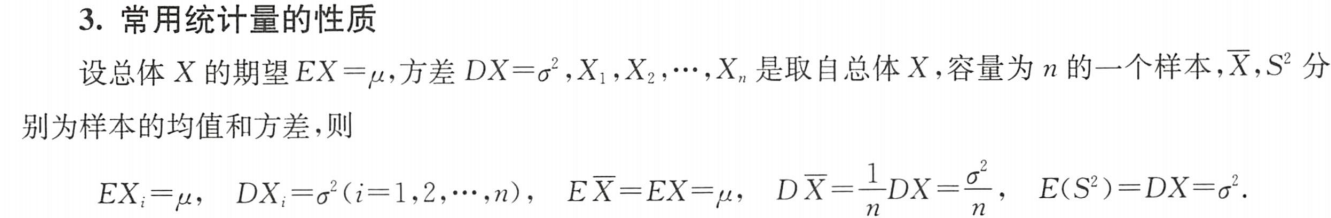概率论与数理统计:第六章:数理统计
文章目录
- Ch6. 数理统计
- (一) 总体与样本
- (二) 统计量 (5个)
- 2.5个常用统计量
- 3.矩的概念
- (三) 抽样分布 (3个)
- 0.上α分位点
- 1.χ²分布
- 2.t分布
- 3.F分布
- (四) 抽样分布定理
- 1.单个正态总体
- 2.两个正态总体
Ch6. 数理统计
(一) 总体与样本
1.概念:
(1)总体

(2)样本
简单随机样本,简称样本。样本与总体 独立同分布。(取自总体的样本,相互之间都独立,且与总体分布相同)

(3)样本的分布

2.性质:
设 X 1 , X 2 , X 3 , . . . , X n ( n > 1 ) X_1,X_2,X_3,...,X_n(n>1) X1,X2,X3,...,Xn(n>1)为来自总体 N(μ,σ²) (σ>0)的简单随机样本(独立同分布), X ‾ = 1 n ∑ i = 1 n X i \overline{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i X=n1i=1∑nXi,则有:
① X i ∼ N ( μ , σ 2 ) X_i\sim N(μ,σ²) Xi∼N(μ,σ2)
② X ‾ ∼ N ( μ , σ 2 n ) \overline{X} \sim N(μ,\dfrac{σ²}{n}) X∼N(μ,nσ2)
③ C o v ( X i , X ‾ ) = σ 2 n {\rm Cov}(X_i,\overline{X})=\dfrac{σ²}{n} Cov(Xi,X)=nσ2
证明:
3.样本与总体 独立同分布,期望相同,方差也相同
①样本的期望与总体的期望相同: E ( X i ) = E ( X ) E(X_i) = E(X) E(Xi)=E(X), ∑ i = 1 n E ( X i ) = n E ( X ) \sum\limits_{i=1}^nE(X_i) = nE(X) i=1∑nE(Xi)=nE(X)
②样本的方差与总体的方差相同: D ( X i ) = D ( X ) D(X_i) = D(X) D(Xi)=D(X), ∑ i = 1 n D ( X i ) = n D ( X ) \sum\limits_{i=1}^nD(X_i) = nD(X) i=1∑nD(Xi)=nD(X)
例题1:18年23(2)
例题2:16年23(1)
(二) 统计量 (5个)
1.概念
(1)统计量的定义

(2)顺序统计量
| 顺序统计量 | 定义 | 分布函数 | 概率密度 |
|---|---|---|---|
| ①第n顺序统计量 X ( n ) X_{(n)} X(n) | m a x { X 1 , X 2 , . . . , X n } max\{X_1,X_2,...,X_n\} max{X1,X2,...,Xn} | [ F ( x ) ] n [F(x)]^n [F(x)]n | n [ F ( x ) ] n − 1 f ( x ) n[F(x)]^{n-1}f(x) n[F(x)]n−1f(x) |
| ②第1顺序统计量 X ( 1 ) X_{(1)} X(1) | m i n { X 1 , X 2 , . . . , X n } min\{X_1,X_2,...,X_n\} min{X1,X2,...,Xn} | 1 − [ 1 − F ( x ) ] n 1-[1-F(x)]^n 1−[1−F(x)]n | n [ 1 − F ( x ) ] n − 1 f ( x ) n[1-F(x)]^{n-1}f(x) n[1−F(x)]n−1f(x) |

2.5个常用统计量
①样本均值: X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i Xˉ=n1i=1∑nXi ∴ ∑ i = 1 n X i = n X ˉ \sum\limits_{i=1}^nX_i=n\bar{X} i=1∑nXi=nXˉ
②样本方差: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S²=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})² S2=n−11i=1∑n(Xi−Xˉ)2 = 1 n − 1 ( ∑ i = 1 n X i 2 − n X ˉ 2 ) =\dfrac{1}{n-1}(\sum\limits_{i=1}^nX_i^2-n\bar{X}^2) =n−11(i=1∑nXi2−nXˉ2), E ( S 2 ) = σ 2 E(S^2)=σ² E(S2)=σ2
样本标准差: S = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S=\sqrt{\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})²} S=n−11i=1∑n(Xi−Xˉ)2
③样本k阶(原点)矩: A k = 1 n ∑ i = 1 n X i k ( k = 1 , 2 , . . . ) A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k (k=1,2,...) Ak=n1i=1∑nXik(k=1,2,...)
④样本k阶中心矩: B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k ( k = 2 , 3 , . . . ) B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k(k=2,3,...) Bk=n1i=1∑n(Xi−Xˉ)k(k=2,3,...)
①k阶原点矩是 ( X i − 0 ) k (X_i-0)^k (Xi−0)k,k阶中心矩是 ( X i − X ˉ ) k (X_i-\bar{X})^k (Xi−Xˉ)k
②样本均值是一阶原点矩,二阶中心矩 B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
3.矩的概念
①原点矩 A
| 样本k阶原点矩 A k A_k Ak | 总体k阶原点矩 |
|---|---|
| A 1 = 1 n ∑ i = 1 n X i = X ˉ A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X} A1=n1i=1∑nXi=Xˉ (样本一阶原点矩,即为均值) | E(X) |
| A 2 = 1 n ∑ i = 1 n X i 2 A_2=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 A2=n1i=1∑nXi2 | E(X²) |
| … | … |
| A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , . . . A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k,k=1,2,... Ak=n1i=1∑nXik,k=1,2,... | E(Xk) |
②中心距 B
| 样本k阶中心矩 B k B_k Bk | 总体k阶中心矩 |
|---|---|
| B 1 = 1 n ∑ i = 1 n ( X i − X ˉ ) B_1=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X}) B1=n1i=1∑n(Xi−Xˉ) | E ( X − E X ) E(X-EX) E(X−EX) |
| B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2 | E [ ( X − E X ) 2 ] = D X E[(X-EX)²]=DX E[(X−EX)2]=DX |
| … | … |
| B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k Bk=n1i=1∑n(Xi−Xˉ)k | E [ ( X − E X ) k ] E[(X-EX)^k] E[(X−EX)k] |
总体矩的矩估计量为样本矩:
①EX的矩估计量为 A 1 = 1 n ∑ i = 1 n X i = X ˉ A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X} A1=n1i=1∑nXi=Xˉ
②DX的矩估计量为 B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
(三) 抽样分布 (3个)
三大抽样分布,均与正态总体有关。总体与样本服从标准正态分布N(0,1)。
0.上α分位点
正态分布的上α分位点: Φ ( Z α 2 ) = 1 − α 2 Φ(Z_{\frac{α}{2}})=1-\dfrac{α}{2} Φ(Z2α)=1−2α


1.χ²分布
1.χ²分布的定义
若 X 1 ∼ N ( 0 , 1 ) X_1\sim N(0,1) X1∼N(0,1),则 X 1 2 ∼ χ 2 ( 1 ) X_1^2\sim χ^2(1) X12∼χ2(1)
设X1,X2,…,Xn为正态总体N(0,1)的样本 ( X i X_i Xi相互独立且同分布),则把统计量
χ 2 = X 1 2 + X 2 2 + . . . + X n 2 χ^2=X_1^2+X_2^2+...+X_n^2 χ2=X12+X22+...+Xn2
服从的分布称为 自由度为n的χ²分布,记作 χ²~χ²(n)
2.χ²分布的上α分位点
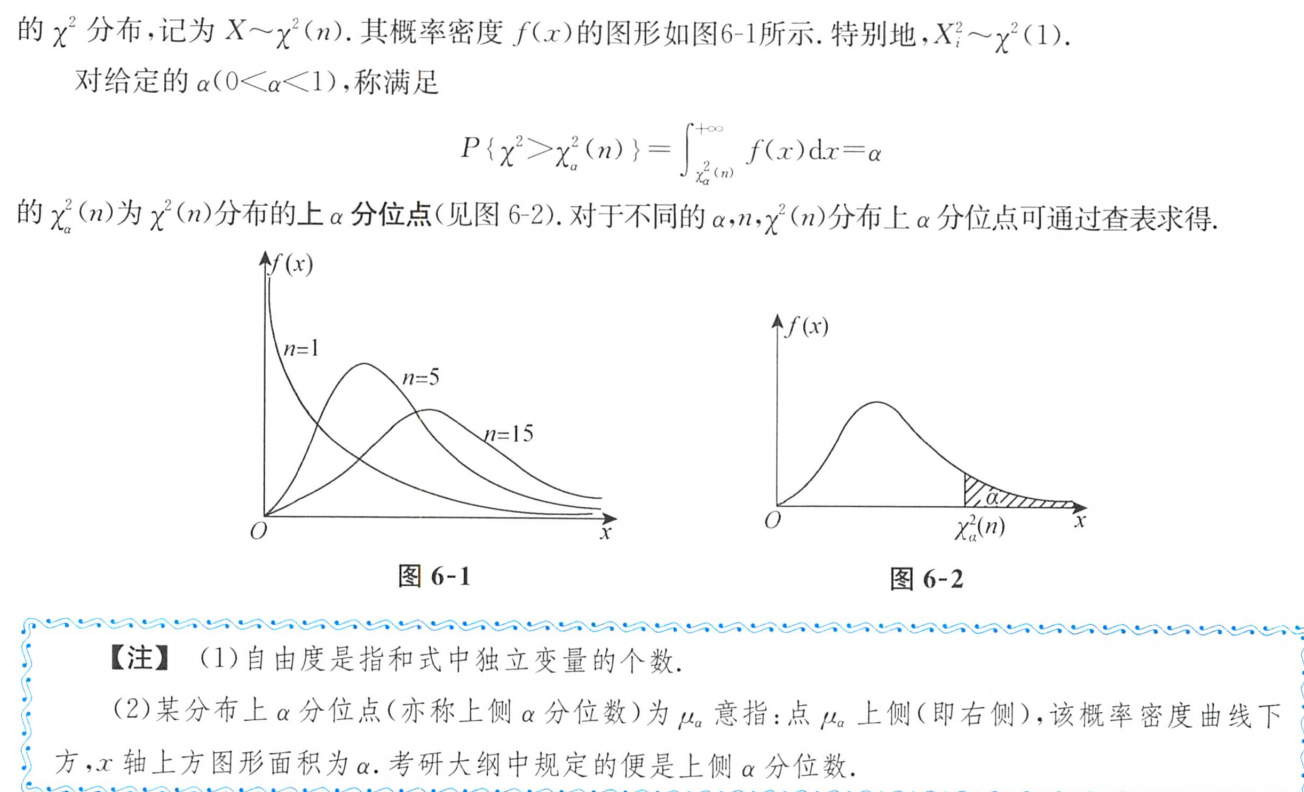
3.χ²分布的性质
- χ²分布的数字特征: E(χ²)=n,D(χ²)=2n
- χ²分布的独立可加性:设 χ 1 2 ∼ χ 2 ( n 1 ) , χ 2 2 ∼ χ 2 ( n 2 ) χ²_1\sim χ²(n_1),χ²_2\sim χ²(n_2) χ12∼χ2(n1),χ22∼χ2(n2),且 χ 1 2 χ²_1 χ12与 χ 2 2 χ²_2 χ22相互独立,则 χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) χ²_1+χ²_2\simχ²(n_1+n_2) χ12+χ22∼χ2(n1+n2)
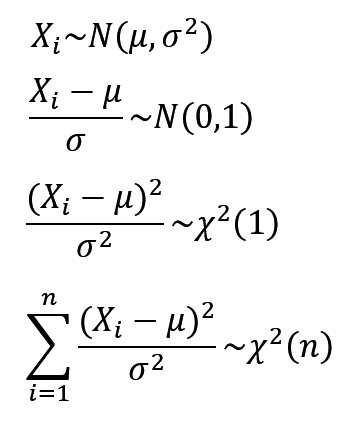
例题1:

分析:

答案: 1 20 \dfrac{1}{20} 201、 1 100 \dfrac{1}{100} 1001、2
例题2:11年23.(2)
2.t分布
1.t分布定义
设 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X\sim N(0,1), Y\sim χ^2(n) X∼N(0,1),Y∼χ2(n),且X,Y相互独立,则把统计量 t = X Y n t=\dfrac{X}{\sqrt{\dfrac{Y}{n}}} t=nYX
服从的分布称为自由度为n的t分布,记作 t ∼ t ( n ) t\sim t(n) t∼t(n)
t(n)的概率密度h(t)关于t=0对称。当自由度n→∞时,t分布的极限就是标准正态分布,n≥30即可
2.t分布的上α分位点
x = t α ( n ) x=t_α(n) x=tα(n)右侧的面积(概率)为α,则称 t α ( n ) t_α(n) tα(n)为上α分位点
x = t 1 − α ( n ) x=t_{1-α}(n) x=t1−α(n)右侧的面积(概率)为1-α,则称 t 1 − α ( n ) t_{1-α}(n) t1−α(n)为上1-α分位点
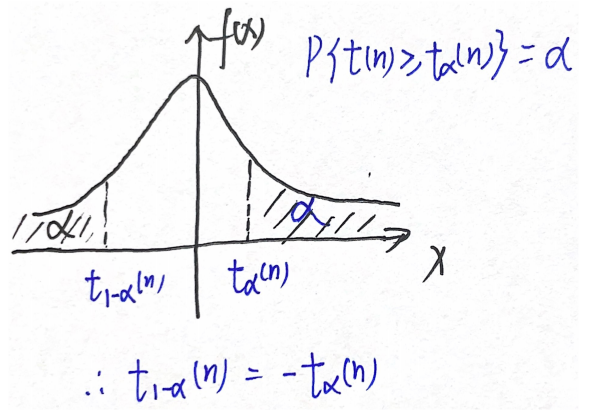
t分布的概率密度是偶函数
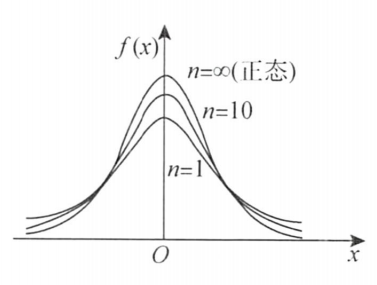
3.t分布性质
1. E ( t ) = 0 E(t)=0 E(t)=0
2.上α分位点: t 1 − α ( n ) = − t α ( n ) t_{1-α}(n)=-t_α(n) t1−α(n)=−tα(n)
3.F分布
1.F分布定义
设 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X\sim χ^2(n_1),Y\sim χ^2(n_2) X∼χ2(n1),Y∼χ2(n2),且X,Y相互独立,则把随机变量 F = X n 1 Y n 2 F=\dfrac{\dfrac{X}{n_1}}{\dfrac{Y}{n_2}} F=n2Yn1X
服从的分布称为自由度为(n1,n2)的F分布,其中n1称为第一自由度,n2称为第二自由度,记作 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2)
2.F分布性质
1.若 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \dfrac{1}{F}\sim F(n_2,n_1) F1∼F(n2,n1)
2.上α分位点: 1 F α ( n 1 , n 2 ) = F 1 − α ( n 2 , n 1 ) \dfrac{1}{F_α(n_1,n_2)}=F_{1-α}(n_2,n_1) Fα(n1,n2)1=F1−α(n2,n1)
3.t分布与F分布的关系
若 t ∼ t ( n ) ,则 t 2 ∼ F ( 1 , n ) , 1 t 2 ∼ F ( n , 1 ) 若t\sim t(n),则t^2\sim F(1,n),\dfrac{1}{t^2}\sim F(n,1) 若t∼t(n),则t2∼F(1,n),t21∼F(n,1)
例题1:03年12. t分布与F分布的关系

分析:
X ∼ t ( n ) , X 2 ∼ F ( 1 , n ) , 1 X 2 ∼ F ( n , 1 ) X\sim t(n),X²\sim F(1,n),\dfrac{1}{X²}\sim F(n,1) X∼t(n),X2∼F(1,n),X21∼F(n,1)
答案:C
例题2:13年8.
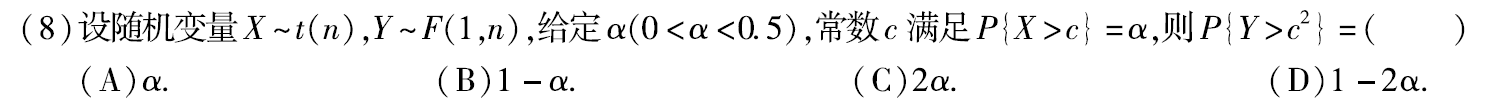
分析:X~t(n), 则 X²=Y~F(1,n)
∴P{Y>c²}=P{X²>c²}=P{X>c}+P{X<-c}=α+α=2α
答案:C
(四) 抽样分布定理
设总体 X ∼ N ( μ , σ 2 ) X\sim N(μ,σ²) X∼N(μ,σ2),样本为 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,独立同分布于总体
1.单个正态总体
1.样本均值: X ˉ ∼ N ( μ , σ 2 n ) \bar{X}\sim N(μ,\dfrac{σ²}{n}) Xˉ∼N(μ,nσ2), X ˉ − μ σ n = ( X ˉ − μ ) n σ ∼ N ( 0 , 1 ) \dfrac{\bar{X}-μ}{\dfrac{σ}{\sqrt{n}}}=\dfrac{(\bar{X}-μ)\sqrt{n}}{σ}\sim N(0,1) nσXˉ−μ=σ(Xˉ−μ)n∼N(0,1)
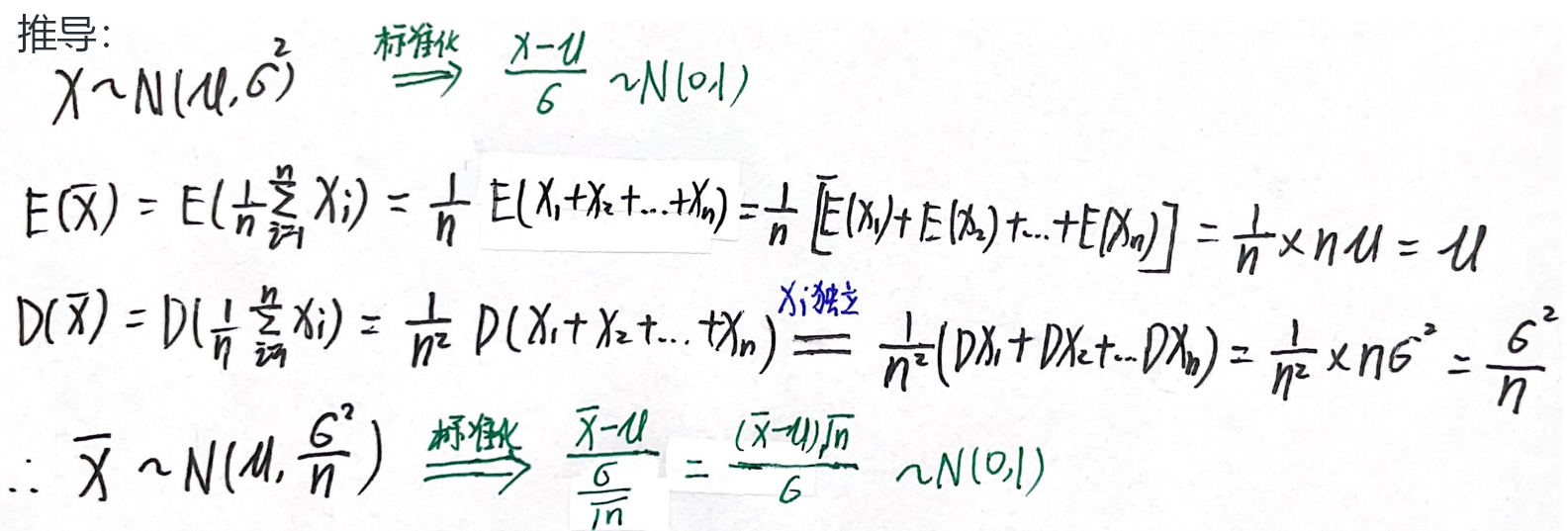
2. ∑ i = 1 n ( X i − μ σ ) 2 ∼ χ 2 ( n ) \sum\limits_{i=1}^n(\dfrac{X_i-μ}{σ})^2\sim \chi^2(n) i=1∑n(σXi−μ)2∼χ2(n)
3. ∑ i = 1 n ( X i − X ‾ σ ) 2 = \sum\limits_{i=1}^n(\dfrac{X_i-\overline{X}}{σ})^2= i=1∑n(σXi−X)2= ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \dfrac{(n-1)S^2}{σ^2}\sim \chi^2(n-1) σ2(n−1)S2∼χ2(n−1)
∴ E ( S 2 ) = σ 2 , D ( S 2 ) = 2 σ 4 n − 1 E(S²)=σ²,D(S²)=\dfrac{2σ^4}{n-1} E(S2)=σ2,D(S2)=n−12σ4
4. ( X ˉ − μ ) S n = n ( X ˉ − μ ) S ∼ t ( n − 1 ) \dfrac{(\bar{X}-μ)}{\dfrac{S}{\sqrt{n}}}=\dfrac{\sqrt{n}(\bar{X}-μ)}{S}\sim t(n-1) nS(Xˉ−μ)=Sn(Xˉ−μ)∼t(n−1)
∴ n ( X ˉ − μ ) 2 S 2 ∼ F ( 1 , n − 1 ) \dfrac{n(\bar{X}-μ)^2}{S^2}\sim F(1,n-1) S2n(Xˉ−μ)2∼F(1,n−1)
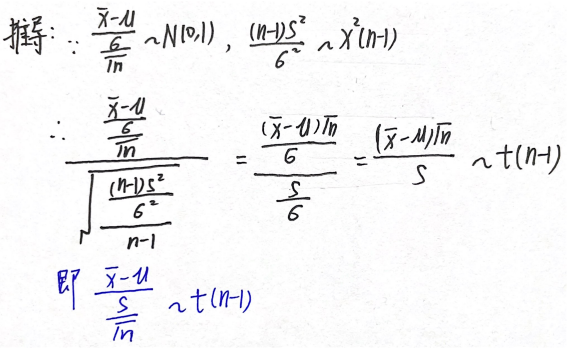
5.样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
例题1:23李林四(四)16.
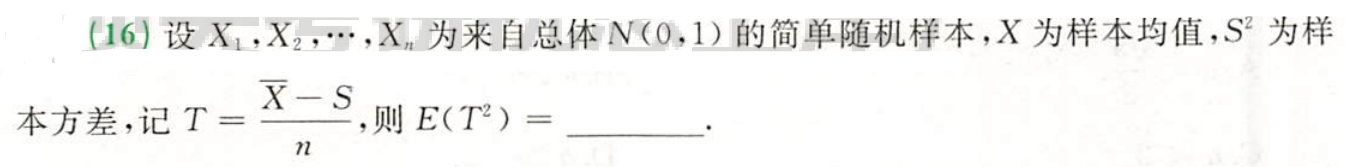
分析:样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
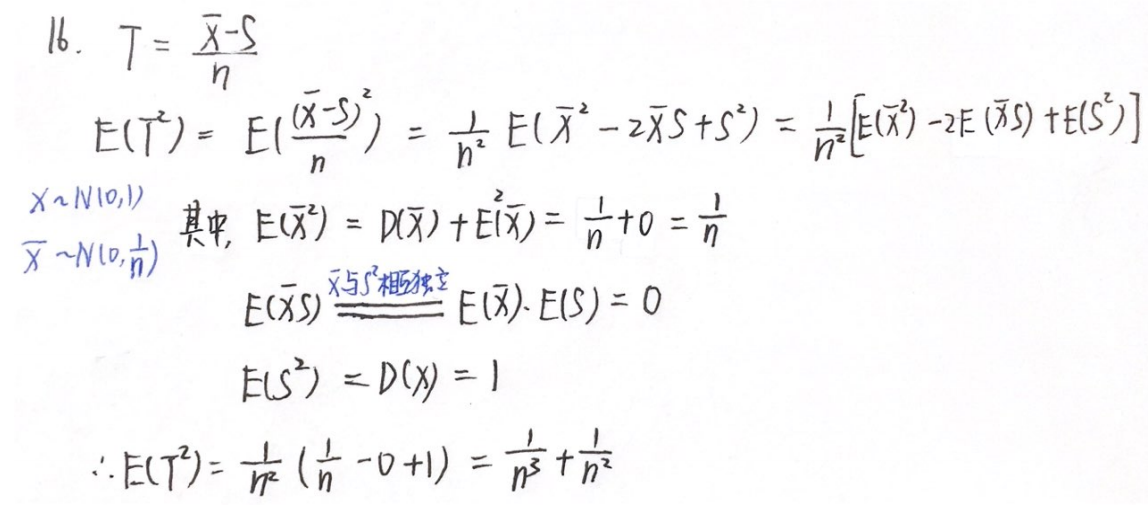
答案: 1 n 3 + 1 n 2 \dfrac{1}{n^3}+\dfrac{1}{n^2} n31+n21
例题2:05年14. 抽样分布定理、F分布

分析:由抽样分布定理得,ABC均错的很离谱。
D: X i ∼ N ( 0 , 1 ) X_i\sim N(0,1) Xi∼N(0,1),即 X i X_i Xi服从标准正态分布
X 1 2 1 ∑ i = 2 n X i 2 n − 1 ∼ F ( 1 , n − 1 ) \dfrac{\frac{X_1^2}{1}}{\frac{\sum\limits_{i=2}^nX_i^2}{n-1}}\sim F(1,n-1) n−1i=2∑nXi21X12∼F(1,n−1),D正确
答案:D
例题3:17年8. 抽样分布定理

分析:

答案:B
例题4:23李林六套卷(六)10.

分析:AB明显正确
C. ( n − 1 ) S 2 σ 2 = ∑ i = 1 n ( X i − X ˉ σ ) 2 ∼ χ 2 ( n − 1 ) \dfrac{(n-1)S^2}{σ^2}=\sum\limits_{i=1}^n(\dfrac{X_i-\bar{X}}{σ})^2\simχ^2(n-1) σ2(n−1)S2=i=1∑n(σXi−Xˉ)2∼χ2(n−1),且卡方分布具有独立可加性,∴C正确
D.应该改为2n-2
答案:D
2.两个正态总体
相关文章:

概率论与数理统计:第六章:数理统计
文章目录 Ch6. 数理统计(一) 总体与样本(二) 统计量 (5个)2.5个常用统计量3.矩的概念 (三) 抽样分布 (3个)0.上α分位点1.χ分布2.t分布3.F分布 (四) 抽样分布定理1.单个正态总体2.两个正态总体 Ch6. 数理统计 (一) 总体与样本 1.概念: (1)总体 (2)样本 简单随机…...
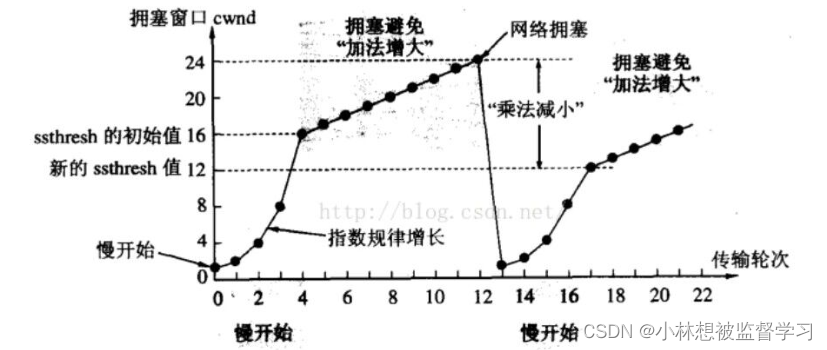
拥塞控制(TCP限制窗口大小的机制)
拥塞控制机制可以使滑动窗口在保证可靠性的前提下,提高传输效率 关于滑动窗口的属性以及部分机制推荐看TCP中窗口和滑动窗口的含义以及流量控制 拥塞控制出现的原因 看了上面推荐的博客我们已经知道了,由于接收方接收数据的能力有限,所以要通…...

校园供水系统智能管理
import pandas as pd data1pd.read_excel("C://Users//JJH//Desktop//E//附件_一季度.xlsx") data2pd.read_excel("C://Users//JJH//Desktop//E//附件_二季度.xlsx") data3pd.read_excel("C://Users//JJH//Desktop//E//附件_三季度.xlsx") data4…...

Flask-SocketIO和Flask-Login联合开发socketio权限系统
设置 Flask, Flask-SocketIO, Flask-Login: 首先,确保安装了必要的库: pip install Flask Flask-SocketIO Flask-Login基础设置: from flask import Flask, render_template, redirect, url_for, request from flask_socketio import SocketIO, emit from flask_…...

航空电子设备中的TSN通讯架构—直升机
前言 以太网正在迅速取代传统网络,成为航空电子设备和任务系统的核心高速网络。本文提出了以太网时间敏感网络(TSN)在航空电子设备上应用的技术优势问题。在实际应用中,TSN已成为一个具有丰富的机制和协议的工具箱,可满足与时间和可靠性相关…...

elment-ui中使用el-steps案例
el-steps案例 样式 代码 <div class"active-box"><div class"active-title">请完善</div><el-steps :active"active" finish-status"success" align-center><el-step title"第一步" /><…...

FPGA解析串口指令控制spi flash完成连续写、读、擦除数据
前言 最近在收拾抽屉时找到一个某宝的spi flash模块,如下图所示,我就想用能不能串口来读写flash,大致过程就是,串口向fpga发送一条指令,fpga解析出指令控制flah,这个指令协议目前就是: 55 AA …...

msvcp120.dll丢失的解决方法,分享三种快速修复的方法
今天,我将和大家分享一个关于电脑问题的解决方法——msvcp120.dll丢失的解决方法。希望对大家有所帮助。 首先,让我们来了解一下msvcp120.dll文件。msvcp120.dll是Microsoft Visual C 2010 Redistributable Package的一个组件,它包含了一些运…...
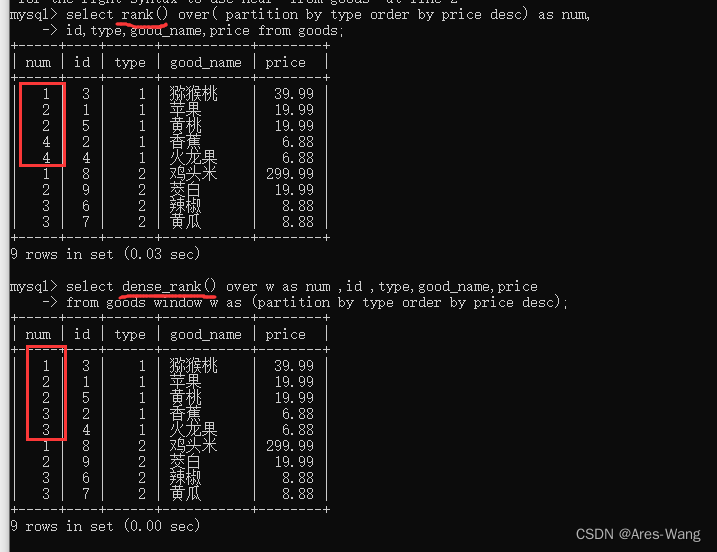
mysql 8.0 窗口函数 之 序号函数 与 sql server 序号函数 一样
sql server 序号函数 序号函数 ROW_NUMBER() 顺序排序RANK() 并列排序,会跳过重复的序号,比如序号为1,1,3DENSE_RANK() 并列排序,不会跳过重复的序号,比如 序号为 1,1,2 语法结构…...
fastgpt构建镜像
1.把client目录复制到服务器 .next和node_modules文件夹不用上传到服务器 在服务器目录运行 docker build -t fastgpt:1.0.3 . 构建服务 再运行 docker ps 就可以看到容器了...

Git笔记--分支常用命令
目录 1--git branch -v 2--git branch 3--git checkout 4--git merge 1--git branch -v git branch -v git branch -v 用于查看分支版本; 2--git branch git branch xxxxx # xxxxx表示分支名 git branch 用于创建分支; 3--git checkout git check…...

常见设计模式学习+面试总结
一 设计模式简介 二 面试总结 1 什么是单例模式?都有哪些地方用到单例? 内存中只会创建且仅创建一次对象的设计模式,保证一个类只有一个实例,并且提供一个访问该全局访问点。 应用场景: 网站的计数器,一般…...

sql解决取多个截至每个月的数据
问题:需要查询1月、1-2月、1-3月… 1-12月,分区间的累计数据,在同一个sql语句里面实现。 多个分开查询效率不高,并且数据手动合并麻烦。 with t1 as ( SELECT *,CASE WHEN insutype 390 THEN 居民 ELSE 职工 END 人员类别,SUBST…...
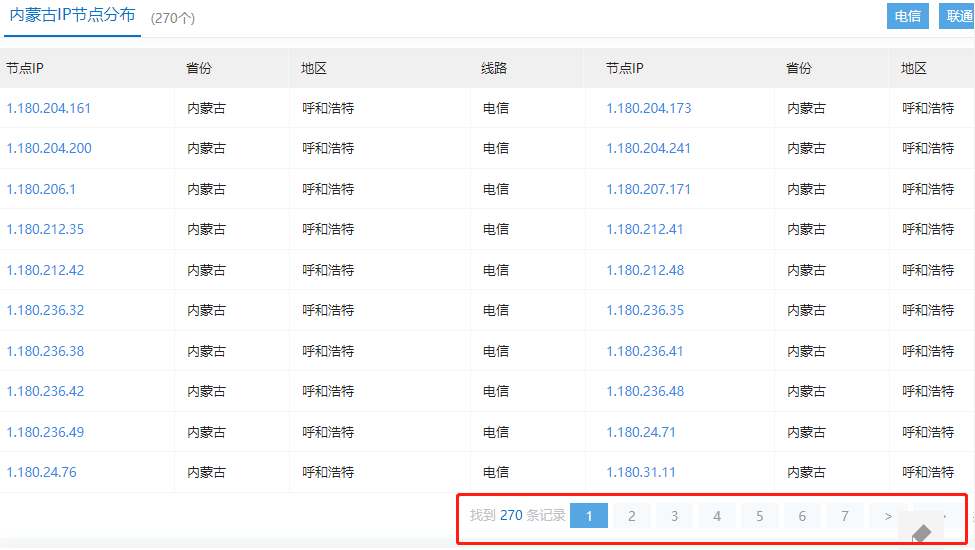
数据采集:selenium 获取 CDN 厂家各省市节点 IP
写在前面 工作需要遇到,简单整理理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃避方式,是对…...
【el-tree】树形组件图标的自定义
饿了么树形组件的图标自定义 默认样式: 可以看到el-tree组件左侧自带展开与收起图标,咱们可以把它隐藏:: .groupList {::v-deep .el-tree-node { .el-icon-caret-right {display: none;} } } 我的全部代码 <div class"groupList"><el…...
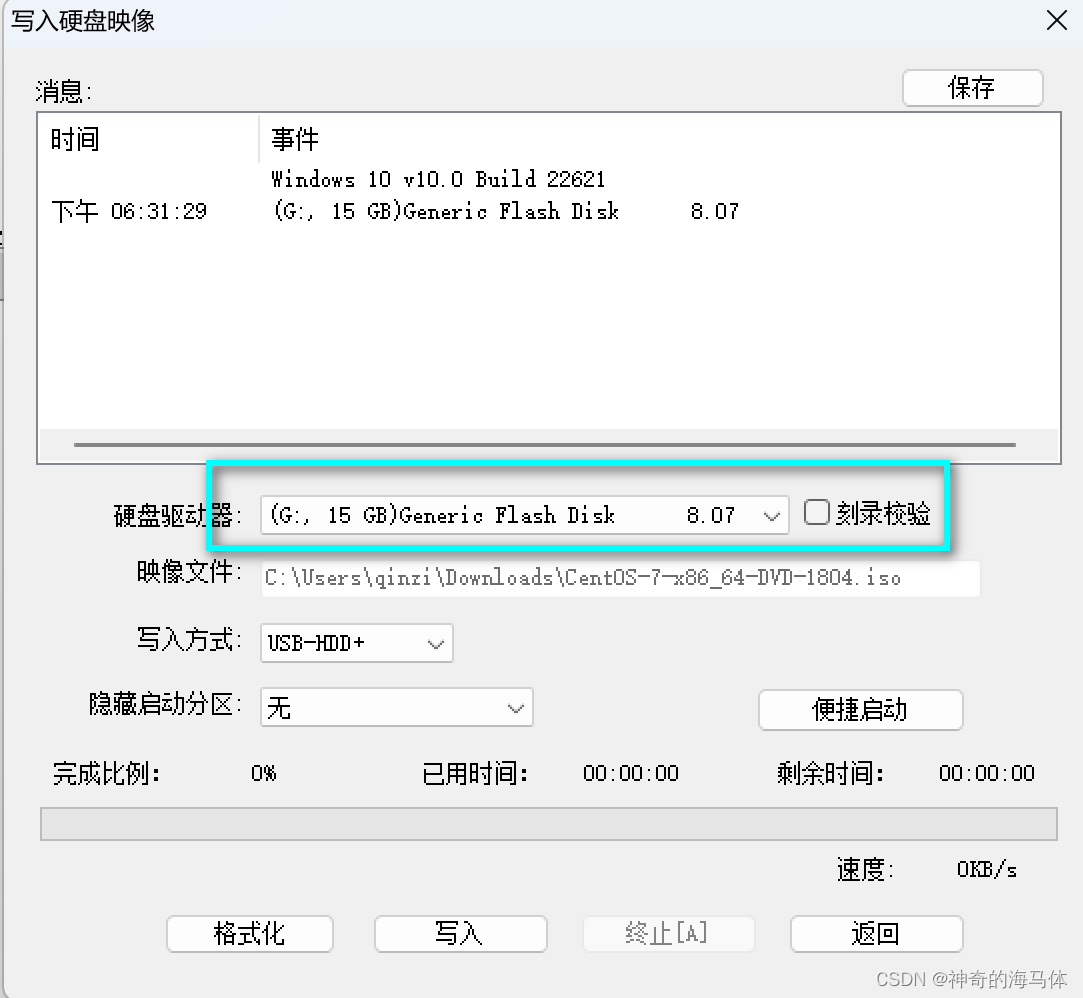
UltralSO软碟通制作Linux系统盘
第一步: 下载镜像 阿里云下载地址:https://mirrors.aliyun.com/centos-vault/ 按照需求选择系统版本,我这要求安装CentOS7.5的系统,我以CentOS7.5为例 第二步: 下载UltralSO软件 官网下载地址:https://cn.…...

yolov8训练心得 持续更新
目录 优化器 lion优化器,学习率0.0001,训练效果: 学习率衰减 600个batch衰减0.7,发现效果较好...
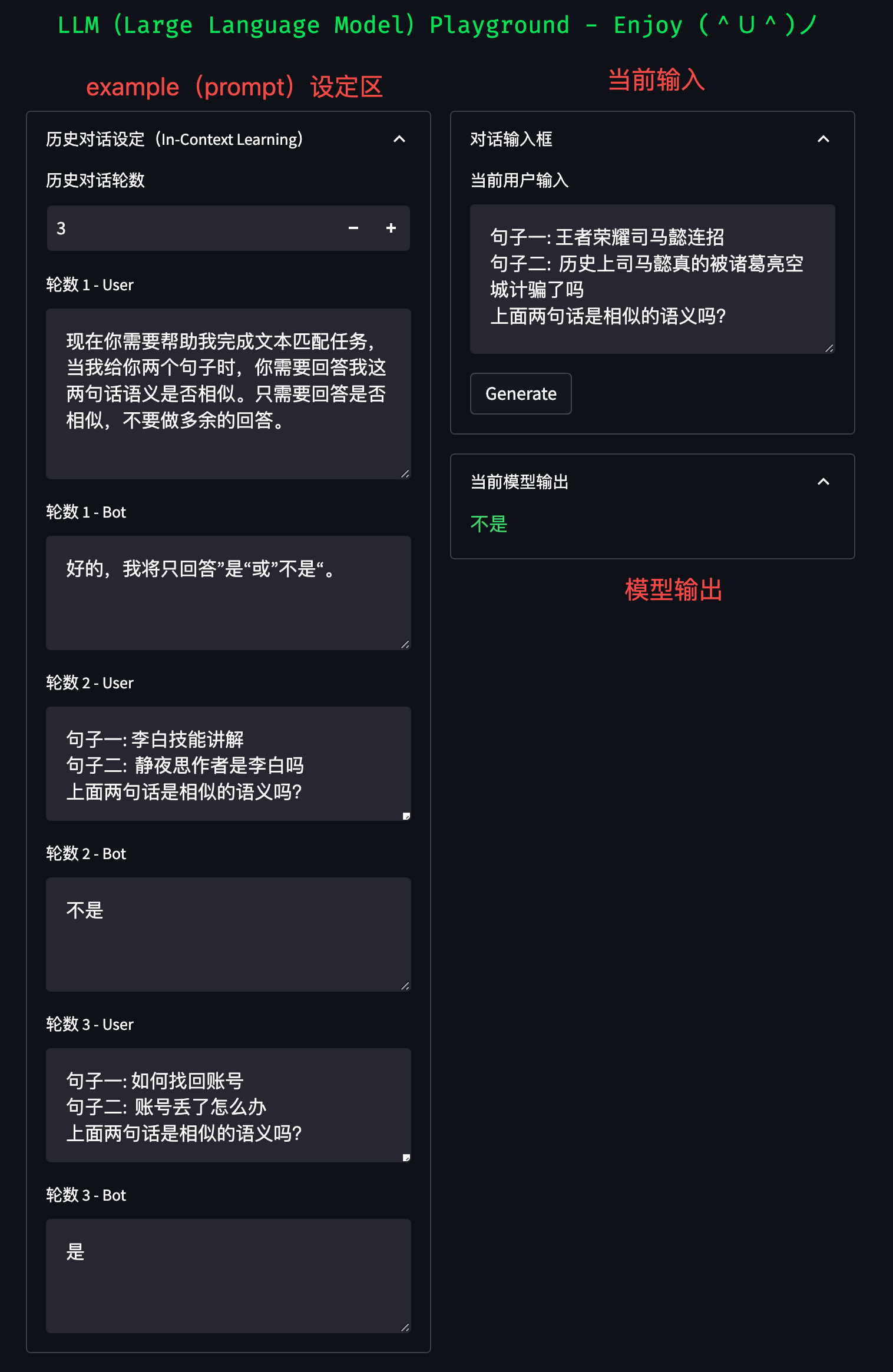
超越界限:大模型应用领域扩展,探索文本分类、文本匹配、信息抽取和性格测试等多领域应用
超越界限:大模型应用领域扩展,探索文本分类、文本匹配、信息抽取和性格测试等多领域应用 随着 ChatGPT 和 GPT-4 等强大生成模型出现,自然语言处理任务方式正在逐步发生改变。鉴于大模型强大的任务处理能力,未来我们或将不再为每…...

Compose - 基本使用
一、概念 1.1 Compose优势 由一个个可以组合的Composable函数拼成界面,方便维护和复用。布局模型不允许多次测量,提升了性能。Compose可以和View互操作(相互包含对方)。 1.2 声明式UI APP展示的数据绝大多数不是静态数据而是会…...
Unity3D Pico VR 手势识别
本文章使用的 Unity3D版本: 2021.3.6 , Pico SDK 230 ,Pico OS v.5.7.1 硬件Pico 4 Pico SDK可以去Pico官网下载SDK 导入SDK 第一步:创建Unity3D项目 第二步:导入 PICO Unity Integration SDK 选择 Windows > Package Manager。 在 Packag…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...