机器学习笔记之优化算法(十九)牛顿法与正则化
机器学习笔记之优化算法——再回首:牛顿法与正则化
- 引言
- 回顾:经典牛顿法及其弊端
- 牛顿法:算法步骤
- 迭代过程中可能出现的问题
- 正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix与相应问题
引言
本节我们介绍经典牛顿法在训练神经网络过程中的迭代步骤,并介绍正则化在牛顿法中的使用逻辑。
回顾:经典牛顿法及其弊端
经典牛顿法自身是一个典型的线搜索方法 ( Line-Search Method ) (\text{Line-Search Method}) (Line-Search Method)。它的迭代过程使用数学符号表示如下:
x k + 1 = x k + α k ⋅ P k x_{k+1} = x_k + \alpha_k \cdot \mathcal P_k xk+1=xk+αk⋅Pk
其中标量 α k \alpha_k αk表示当前第 k k k次迭代情况下的更新步长;向量 P k \mathcal P_k Pk表示当前迭代步骤的更新方向。与梯度下降法区分的是,在经典牛顿法中:
- 步长并不是我们关注的信息,我们通常设置 α k = 1 ( k = 1 , 2 , 3 , ⋯ ) \alpha_k = 1(k=1,2,3,\cdots) αk=1(k=1,2,3,⋯),从而迭代结果 x k + 1 x_{k+1} xk+1可看作是关于方向变量 P \mathcal P P的函数:
而P k \mathcal P_k Pk则表示当前迭代步骤的最优更新方向。
{ x k + 1 = x k + P P k = arg min P f ( x k + 1 ) = arg min P f ( x k + P ) \begin{cases} \begin{aligned} x_{k+1} & = x_k + \mathcal P \\ \mathcal P_k & = \mathop{\arg\min}\limits_{\mathcal P} f(x_{k+1}) \\ & = \mathop{\arg\min}\limits_{\mathcal P} f(x_k + \mathcal P) \end{aligned} \end{cases} ⎩ ⎨ ⎧xk+1Pk=xk+P=Pargminf(xk+1)=Pargminf(xk+P) - 关于目标函数 f ( ⋅ ) f(\cdot) f(⋅),我们对其要求是: f ( ⋅ ) f(\cdot) f(⋅)至少二阶可微。这意味着 Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(\cdot) Hessian Matrix⇒∇2f(⋅)存在。因此对目标函数 f ( x k + P ) f(x_k + \mathcal P) f(xk+P)进行二阶泰勒展开:
f ( x k + P ) = ϕ ( P ) = f ( x k ) + 1 1 ! [ ∇ f ( x k ) ] T P + 1 2 ! P T [ ∇ 2 f ( x k ) ] ⋅ P + O ( ∥ P ∥ 2 ) f(x_k + \mathcal P) = \phi(\mathcal P) = f(x_k) + \frac{1}{1!} [\nabla f(x_k)]^T \mathcal P + \frac{1}{2!} \mathcal P^T [\nabla^2 f(x_k)] \cdot \mathcal P + \mathcal O(\|\mathcal P\|^2) f(xk+P)=ϕ(P)=f(xk)+1!1[∇f(xk)]TP+2!1PT[∇2f(xk)]⋅P+O(∥P∥2)
忽略掉高阶无穷小 O ( ∥ P ∥ 2 ) \mathcal O(\|\mathcal P\|^2) O(∥P∥2),通过令 ∇ ϕ ( P ) ≜ 0 \nabla \phi(\mathcal P) \triangleq 0 ∇ϕ(P)≜0来求解 P k \mathcal P_k Pk,使 ϕ ( P k ) \phi(\mathcal P_k) ϕ(Pk)取得最小值:
∇ ϕ ( P ) ≜ 0 ⇒ ∇ 2 f ( x k ) ⋅ P = − ∇ f ( x k ) \nabla \phi(\mathcal P) \triangleq 0 \Rightarrow \nabla^2 f(x_k) \cdot \mathcal P = -\nabla f(x_k) ∇ϕ(P)≜0⇒∇2f(xk)⋅P=−∇f(xk)
我们称该方程组为牛顿方程:- 如果 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)在 x k x_k xk出的 Hessian Matrix ⇒ ∇ 2 f ( x k ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x_k) Hessian Matrix⇒∇2f(xk)是正定矩阵,那么:本次迭代步骤存在合适的 P k \mathcal P_k Pk,使 ϕ ( P k ) \phi(\mathcal P_k) ϕ(Pk)达到最小值:
需要注意的是,这仅仅是当前迭代步骤的最小值,而不是全局最小值。
P k = − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) \mathcal P_k = - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) Pk=−[∇2f(xk)]−1∇f(xk)
并且解 P k \mathcal P_k Pk描述的方向一定是下降方向。 - 相反,如果 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)不是正定矩阵,那么至少说:无法直接求解,方程组 ∇ 2 f ( x k ) ⋅ P = − ∇ f ( x k ) \nabla^2 f(x_k) \cdot \mathcal P = -\nabla f(x_k) ∇2f(xk)⋅P=−∇f(xk)的解是 P k \mathcal P_k Pk的解。
- 如果 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)在 x k x_k xk出的 Hessian Matrix ⇒ ∇ 2 f ( x k ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x_k) Hessian Matrix⇒∇2f(xk)是正定矩阵,那么:本次迭代步骤存在合适的 P k \mathcal P_k Pk,使 ϕ ( P k ) \phi(\mathcal P_k) ϕ(Pk)达到最小值:
牛顿法:算法步骤
在训练神经网络的方法中,牛顿法是二阶近似方法的代表。这里为了简单表述,将上面提到的目标函数 f ( ⋅ ) f(\cdot) f(⋅)具象化为经验风险 ( Empirical Risk ) (\text{Empirical Risk}) (Empirical Risk):
J ( θ ) = E P d a t a { L [ G ( x ( i ) ; θ ) , y ( i ) ] } = 1 N ∑ i = 1 N L [ G ( x ( i ) ; θ ) , y ( i ) ] P d a t a = { ( x ( i ) , y ( i ) ) } i = 1 N \begin{aligned} \mathcal J(\theta) & = \mathbb E_{\mathcal P_{data}} \left\{\mathcal L[\mathcal G(x^{(i)};\theta),y^{(i)}]\right\} \\ & = \frac{1}{N} \sum_{i=1}^N \mathcal L [\mathcal G(x^{(i)};\theta),y^{(i)}] \end{aligned}\quad P_{data} = \{(x^{(i)},y^{(i)})\}_{i=1}^N J(θ)=EPdata{L[G(x(i);θ),y(i)]}=N1i=1∑NL[G(x(i);θ),y(i)]Pdata={(x(i),y(i))}i=1N
其中 θ \theta θ可看作是需要学习的模型参数; G ( ⋅ ) \mathcal G(\cdot) G(⋅)可看作是模型关于 x x x的预测函数; L ( ⋅ ) \mathcal L(\cdot) L(⋅)可看作是损失函数,描述预测结果与真实标签的差异性信息。
假设 θ 0 \theta_0 θ0表示当前迭代过程的起始位置,是已知项;而 θ \theta θ是一个变量,描述当前迭代过程结束后的参数位置。这里直接使用: θ − θ 0 \theta -\theta_0 θ−θ0表示当前迭代步骤的更新方向,对 J ( θ ) \mathcal J(\theta) J(θ)进行二阶泰勒展开:
实际上,书中θ − θ 0 \theta - \theta_0 θ−θ0本身就将步长 α = 1 \alpha = 1 α=1包含在内。这里关于J ( θ ) \mathcal J(\theta) J(θ)高于二阶的高阶无穷小直接省略掉了~关于Hessian Matrix ⇒ ∇ 2 J ( θ 0 ) \text{Hessian Matrix} \Rightarrow \nabla^2 \mathcal J(\theta_0) Hessian Matrix⇒∇2J(θ0)直接使用H \mathcal H H进行表示。
J ( θ ) ≈ J ( θ 0 ) + 1 1 ! ( θ − θ 0 ) T ∇ θ J ( θ 0 ) + 1 2 ! ( θ − θ 0 ) T H ( θ − θ 0 ) \mathcal J(\theta) \approx \mathcal J(\theta_0) + \frac{1}{1!}(\theta - \theta_0)^T \nabla_{\theta} \mathcal J(\theta_0) + \frac{1}{2!}(\theta - \theta_0)^T \mathcal H (\theta - \theta_0) J(θ)≈J(θ0)+1!1(θ−θ0)T∇θJ(θ0)+2!1(θ−θ0)TH(θ−θ0)
依然令 ∇ J ( θ ) ≜ 0 \nabla \mathcal J(\theta) \triangleq 0 ∇J(θ)≜0,有:
∇ J ( θ ) = ( 1 − 0 ) ⋅ ∇ J θ ( θ 0 ) + 1 2 ⋅ 2 ( θ − θ 0 ) ⋅ H ≜ 0 ⇒ H ( θ − θ 0 ) = − ∇ J θ ( θ 0 ) \begin{aligned} \nabla\mathcal J(\theta) & = (1 - 0) \cdot \nabla \mathcal J_{\theta}(\theta_0) + \frac{1}{2} \cdot 2 (\theta - \theta_0)\cdot \mathcal H \triangleq 0\\ & \Rightarrow \mathcal H(\theta - \theta_0) = -\nabla \mathcal J_{\theta}(\theta_0) \end{aligned} ∇J(θ)=(1−0)⋅∇Jθ(θ0)+21⋅2(θ−θ0)⋅H≜0⇒H(θ−θ0)=−∇Jθ(θ0)
假设 H \mathcal H H是正定的条件下,关于 θ \theta θ与 θ 0 \theta_0 θ0的递推关系表示如下:
θ = θ 0 − H − 1 ∇ θ J ( θ 0 ) \theta = \theta_0 - \mathcal H^{-1} \nabla_{\theta} \mathcal J(\theta_0) θ=θ0−H−1∇θJ(θ0)
基于递推关系,对应的算法步骤表示如下:
-
初始化:初始参数 θ s t a r t \theta_{start} θstart以及包含 N N N个样本的训练数据集;
-
While \text{While} While:
- 计算 ∇ θ J ( θ 0 ) \nabla_{\theta} \mathcal J(\theta_0) ∇θJ(θ0):
牛顿-莱布尼兹公式~,这是书上的表达。详细位置见末尾~
∇ θ J ( θ 0 ) = ∇ θ { 1 N ∑ i = 1 N L [ G ( x ( i ) ; θ 0 ) , y ( i ) ] } = 1 N ∇ θ ∑ i = 1 N L [ G ( x ( i ) ; θ 0 ) , y ( i ) ] \begin{aligned} \nabla_{\theta} \mathcal J(\theta_0) & = \nabla_{\theta} \left\{\frac{1}{N} \sum_{i=1}^N \mathcal L[\mathcal G(x^{(i)};\theta_0),y^{(i)}]\right\} \\ & = \frac{1}{N} \nabla_{\theta} \sum_{i=1}^N \mathcal L[\mathcal G(x^{(i)};\theta_0),y^{(i)}] \end{aligned} ∇θJ(θ0)=∇θ{N1i=1∑NL[G(x(i);θ0),y(i)]}=N1∇θi=1∑NL[G(x(i);θ0),y(i)] - 计算 θ 0 \theta_0 θ0位置的 Hessian Matrix ⇒ H \text{Hessian Matrix} \Rightarrow \mathcal H Hessian Matrix⇒H:
该公式同样也是书上描述。
H = ∇ θ 2 J ( θ 0 ) = ∇ θ 2 { 1 N ∑ i = 1 N L [ G ( x ( i ) ; θ 0 ) , y ( i ) ] } = 1 N ∇ θ 2 ∑ i = 1 N L [ G ( x ( i ) ; θ 0 ) , y ( i ) ] \begin{aligned} \mathcal H & = \nabla_{\theta}^2 \mathcal J(\theta_0) \\ & = \nabla_{\theta}^2 \left\{\frac{1}{N} \sum_{i=1}^N \mathcal L[\mathcal G(x^{(i)};\theta_0),y^{(i)}]\right\} \\ & = \frac{1}{N} \nabla_{\theta}^2 \sum_{i=1}^N \mathcal L[\mathcal G(x^{(i)};\theta_0),y^{(i)}] \end{aligned} H=∇θ2J(θ0)=∇θ2{N1i=1∑NL[G(x(i);θ0),y(i)]}=N1∇θ2i=1∑NL[G(x(i);θ0),y(i)] - 计算 Hessian Matrix \text{Hessian Matrix} Hessian Matrix的逆: H − 1 \mathcal H^{-1} H−1;
- 计算变量 θ \theta θ的变化量 Δ θ \Delta \theta Δθ:
Δ θ = − H − 1 ∇ θ J ( θ 0 ) \Delta \theta = -\mathcal H^{-1} \nabla_{\theta} \mathcal J(\theta_0) Δθ=−H−1∇θJ(θ0) - 对变量 θ \theta θ进行更新:
θ = θ 0 + Δ θ \theta = \theta_0 + \Delta \theta θ=θ0+Δθ
- 计算 ∇ θ J ( θ 0 ) \nabla_{\theta} \mathcal J(\theta_0) ∇θJ(θ0):
-
End While \text{End While} End While
迭代过程中可能出现的问题
观察上述迭代步骤,一个核心问题是:该算法必须建立在迭代过程中,各步骤的 θ \theta θ对应的 Hessian Matrix \text{Hessian Matrix} Hessian Matrix必须均是正定的,否则 H − 1 \mathcal H^{-1} H−1无法求解。在凸函数 VS \text{VS} VS强凸函数中介绍过关于强凸函数的二阶条件:如果函数 f ( ⋅ ) f(\cdot) f(⋅)二阶可微,有:
其中 I \mathcal I I表示单位矩阵。
f ( ⋅ ) is m-Strong Convex ⇔ ∇ 2 f ( x ) ≽ m ⋅ I f(\cdot) \text{is m-Strong Convex} \Leftrightarrow \nabla^2 f(x) \succcurlyeq m \cdot \mathcal I f(⋅)is m-Strong Convex⇔∇2f(x)≽m⋅I
也就是说:要想 H = ∇ θ 2 J ( θ 0 ) \mathcal H = \nabla_{\theta}^2 \mathcal J(\theta_0) H=∇θ2J(θ0)正定,必然需要目标函数 J ( θ ) \mathcal J(\theta) J(θ)在 θ = θ 0 \theta= \theta_0 θ=θ0处不仅是凸的,甚至是强凸的。
但在深度学习中,目标函数的表面由于特征较多,从而在局部呈现非凸的情况。例如鞍点,二阶梯度函数 ∇ θ 2 J ( θ ) \nabla_{\theta}^2 \mathcal J(\theta) ∇θ2J(θ)在该处的特征值并不都是正的,也就是说:鞍点处的 Hessian Matrix \text{Hessian Matrix} Hessian Matrix可能不是正定的,从而可能导致在该点出迭代过程中选择的 θ \theta θ,使得更新方向 θ − θ 0 \theta - \theta_0 θ−θ0是个错误的方向。
正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix与相应问题
上述情况可以使用正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix来避免。一种常用的正则化策略是 Hessian Matrix \text{Hessian Matrix} Hessian Matrix加上一个对角线元素均为 α \alpha α的对角阵:
θ = θ 0 − [ ∇ θ 2 J ( θ 0 ) ⏟ H + α ⋅ I ] − 1 ∇ θ J ( θ 0 ) \theta = \theta_0 - \left[\underbrace{\nabla_{\theta}^2 \mathcal J(\theta_0)}_{\mathcal H} + \alpha \cdot \mathcal I\right]^{-1} \nabla_{\theta} \mathcal J(\theta_0) θ=θ0− H ∇θ2J(θ0)+α⋅I −1∇θJ(θ0)
这种操作我们早在正则化与岭回归中就已介绍过。由于 Hessian Matrix ⇒ H \text{Hessian Matrix} \Rightarrow \mathcal H Hessian Matrix⇒H至少是实对称矩阵,那么必然有:
H = Q Λ Q T Q Q T = Q T Q = I \mathcal H = \mathcal Q\Lambda \mathcal Q^T \quad \mathcal Q\mathcal Q^T = \mathcal Q^T\mathcal Q = \mathcal I H=QΛQTQQT=QTQ=I
并且 λ I = Q ( λ I ) Q T \lambda \mathcal I = \mathcal Q(\lambda \mathcal I) \mathcal Q^T λI=Q(λI)QT,从而 H + λ ⋅ I \mathcal H + \lambda \cdot \mathcal I H+λ⋅I可表示为:
H + λ ⋅ I = Q Λ Q T + Q ( λ I ) Q T = Q ( Λ + λ I ) Q T \begin{aligned} \mathcal H + \lambda \cdot \mathcal I & = \mathcal Q \Lambda\mathcal Q^T + \mathcal Q(\lambda \mathcal I) \mathcal Q^T \\ & = \mathcal Q(\Lambda + \lambda \mathcal I) \mathcal Q^T \end{aligned} H+λ⋅I=QΛQT+Q(λI)QT=Q(Λ+λI)QT
这相当于:给 H \mathcal H H的所有特征值加上一个正值 α \alpha α。
相比于最小二乘法模型参数 W \mathcal W W的矩阵形式表达: W = ( X T X ) − 1 X T Y \mathcal W = (\mathcal X^T \mathcal X)^{-1} \mathcal X^T \mathcal Y W=(XTX)−1XTY, H \mathcal H H可能更不稳定。因为 X T X \mathcal X^T\mathcal X XTX必然是半正定的,但 H \mathcal H H中的特征值有可能是负的。
由于 H \mathcal H H中的特征值有可能是负的,甚至是负定矩阵。如果 H \mathcal H H中存在特征值负的很厉害的情况下(存在很强的负曲率),我们需要增大 α \alpha α结果来抵消负特征值。如果 α \alpha α持续增大,对应特征值可能会被 α \alpha α主导。从而导致迭代步骤选择的方向收敛到 1 α × \begin{aligned}\frac{1}{\alpha} \times\end{aligned} α1×普通梯度。
使用牛顿法训练大型的神经网络,更多还受限于计算负担。由于 H ∈ R p × p \mathcal H \in \mathbb R^{p \times p} H∈Rp×p,其中 p p p表示样本特征维度,求解 H − 1 \mathcal H^{-1} H−1的时间复杂度是 O ( k 3 ) \mathcal O(k^3) O(k3)。并且由于迭代过程中随着 θ \theta θ的变化,因而需要每次迭代过程都要计算对应 H − 1 \mathcal H^{-1} H−1。因而,最终结果是:只有少量参数的神经网络,才能在实际中使用牛顿法进行训练。
相关参考:
《深度学习》(花书)P190 - 8.6 二阶近似方法
相关文章:
牛顿法与正则化)
机器学习笔记之优化算法(十九)牛顿法与正则化
机器学习笔记之优化算法——再回首:牛顿法与正则化 引言回顾:经典牛顿法及其弊端牛顿法:算法步骤迭代过程中可能出现的问题正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix与相应问题 引言 本节我们介绍经典牛顿法在训练神经网络过程中的迭…...

Java面试之单例模式的六种实现方式
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、为什么要用单例模式二、单例模式的六种实现2.1 饿汉式2.1.1 饿汉式代码实现2.1.2 饿汉式代码实现要点解析2.1.3 饿汉式代码实现优点2.1.4 饿汉式代码实现缺…...

re正则入门
🌸re正则入门 正则表达式 (Regular Expression) 又称 RegEx, 是用来匹配字符的一种工具. 在一大串字符中寻找你需要的内容. 它常被用在很多方面, 比如网页爬虫, 文稿整理, 数据筛选等等 简单的匹配 正则表达式无非就是在做这么一回事. 在文字中找到特定的内容, 比如…...

C++ Day5
目录 一、静态成员 1.1 概念 1.2 格式 1.3 银行账户实例 二、类的继承 2.1 目的 2.2 概念 2.3 格式 2.4 继承方式 2.5 继承中的特殊成员函数 2.5.1 构造函数 2.5.2析构函数 2.5.3 拷贝构造函数 2.5.4拷贝赋值函数 总结: 三、多继承 3.1 概念 3.2 格…...

el-element:自定义参数
希望在下拉框、输入框、多选框中添加自定义参数,这在项目中是非常常见的 1、 Select选择器中remote-method方法带自定义参数 :remote-method"(query)>{remoteMethod(query,自定义参数)}" remoteMethod(query, pid){ } 2、 el多选框方法追加参数&…...

“分布式”与“集群”初学者的技术总结
一、“分布式”与“集群”的解释: 分布式:把一个囊肿的系统分成无数个单独可运行的功能模块 集群: 把相同的项目复制进行多次部署(可以是一台服务器多次部署,例如使用8080部署一个,8081部署一个,…...
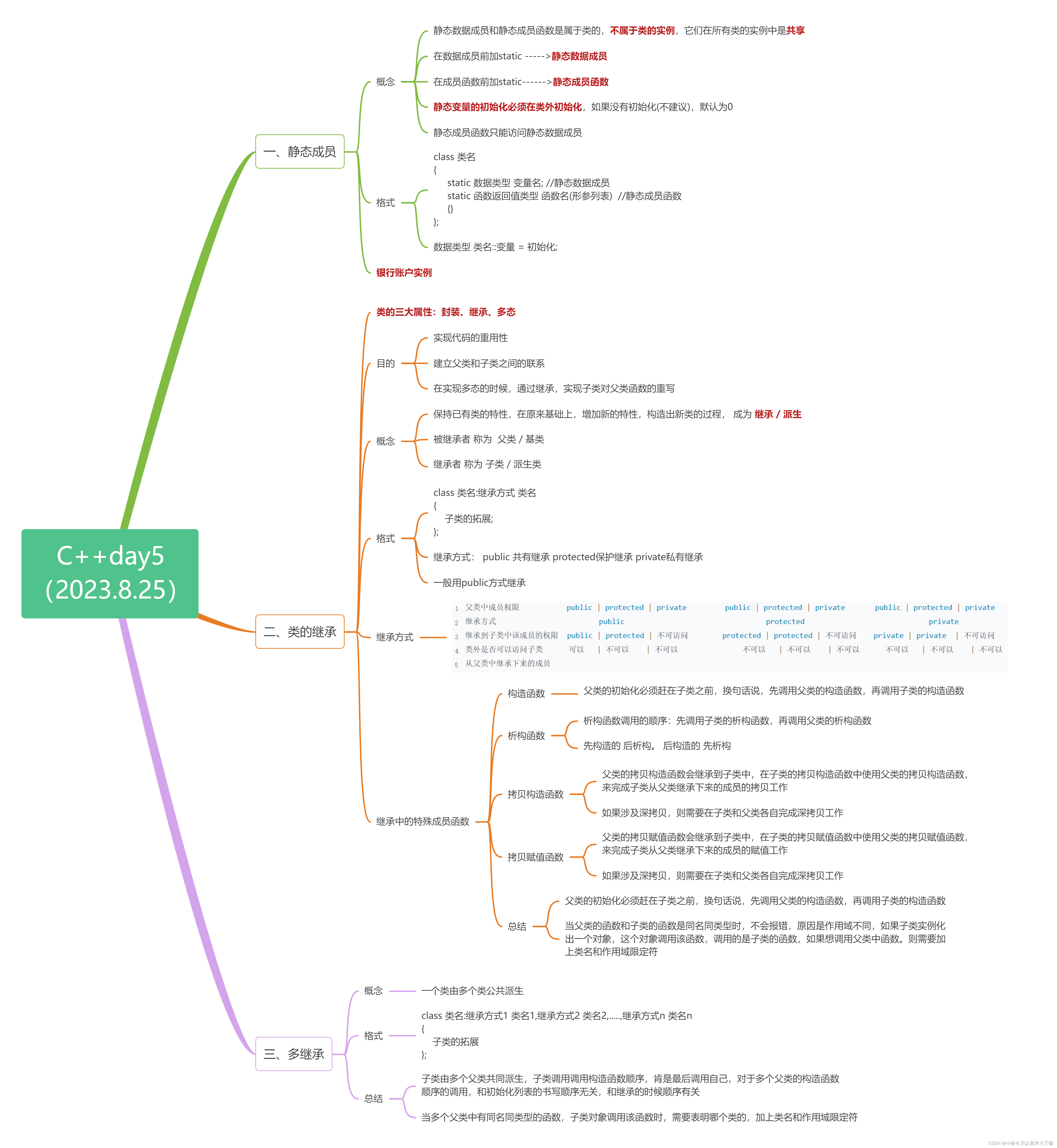
C++day5(静态成员、类的继承、多继承)
一、Xmind整理: 二、上课笔记整理: 1.静态数据成员静态成员函数(银行账户实例) #include <iostream>using namespace std;class BankAccount { private:double balance; //余额static double interest_rate; //利率 p…...

2023MySQL+MyBatis知识点整理
文章目录 主键 外键 的区别?什么是范式?什么是反范式?什么是事务?MySQL事务隔离级别?MySQL事务默认提交模式?MySQL中int(1)和int(10)的区别MySQL 浮点数会丢失精度吗?MySQL支持哪几种时间类型&a…...
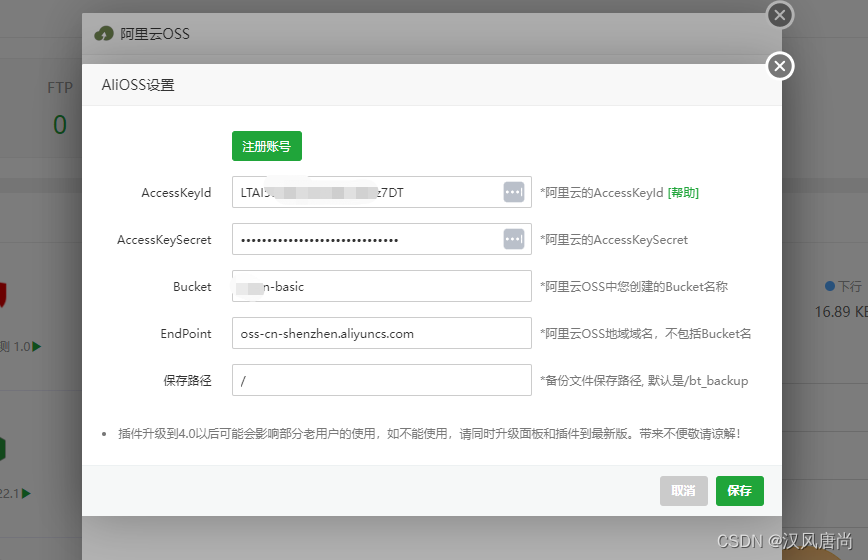
【随笔】如何使用阿里云的OSS保存基础的服务器环境
使用阿里云OSS创建一个存储仓库:bucket 在Linux上下载并安装阿里云的ossutil工具 // 命令行,是linux环境 3. 安装ossutil。sudo -v ; curl https://gosspublic.alicdn.com/ossutil/install.sh | sudo bash 说明:安装过程中,需要使用解压工具…...

汽车电子笔记之:AUTOSA架构下的多核OS操作系统
目录 1、AUTOSAR多核操作系统 1.1、OS Application 1.2、多核OS的软件分区 1.3、任务调度 1.4、核间任务同步 1.5、计数器、报警器、调度表 1.6、自旋锁与共享资源 1.7、核间通信IOC 1.8、OS Object中元素交互 1.9、多核OS的启动与关闭 2、多核OS注意事项 2.1、最小…...
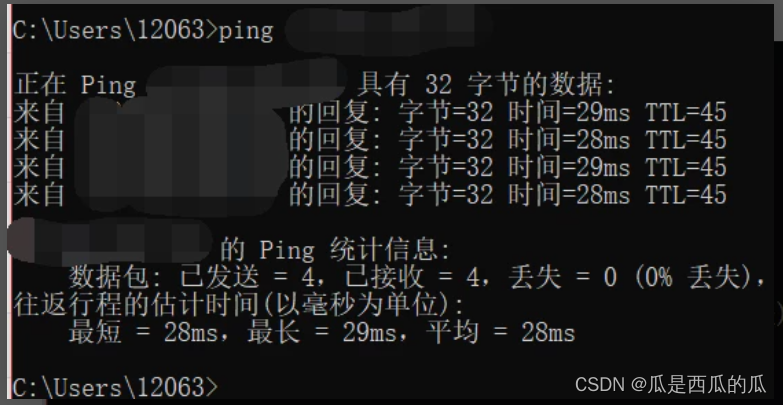
解决华为云ping不通的问题
进入华为云控制台。依次选择:云服务器->点击服务器id->安全组->更改安全组->添加入方向规则,添加一个安全组规则(ICMP),详见下图 再次ping公网ip就可以ping通了 产生这一问题的原因是ping的协议基于ICMP协…...
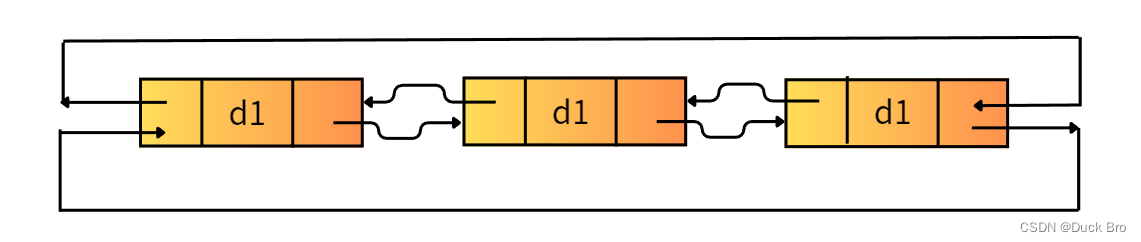
数据结构入门 — 链表详解_双向链表
前言 数据结构入门 — 双向链表详解* 博客主页链接:https://blog.csdn.net/m0_74014525 关注博主,后期持续更新系列文章 文章末尾有源码 *****感谢观看,希望对你有所帮助***** 系列文章 第一篇:数据结构入门 — 链表详解_单链表…...

时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比) 目录 时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)预测效果基本介绍模型介绍程序设计参…...
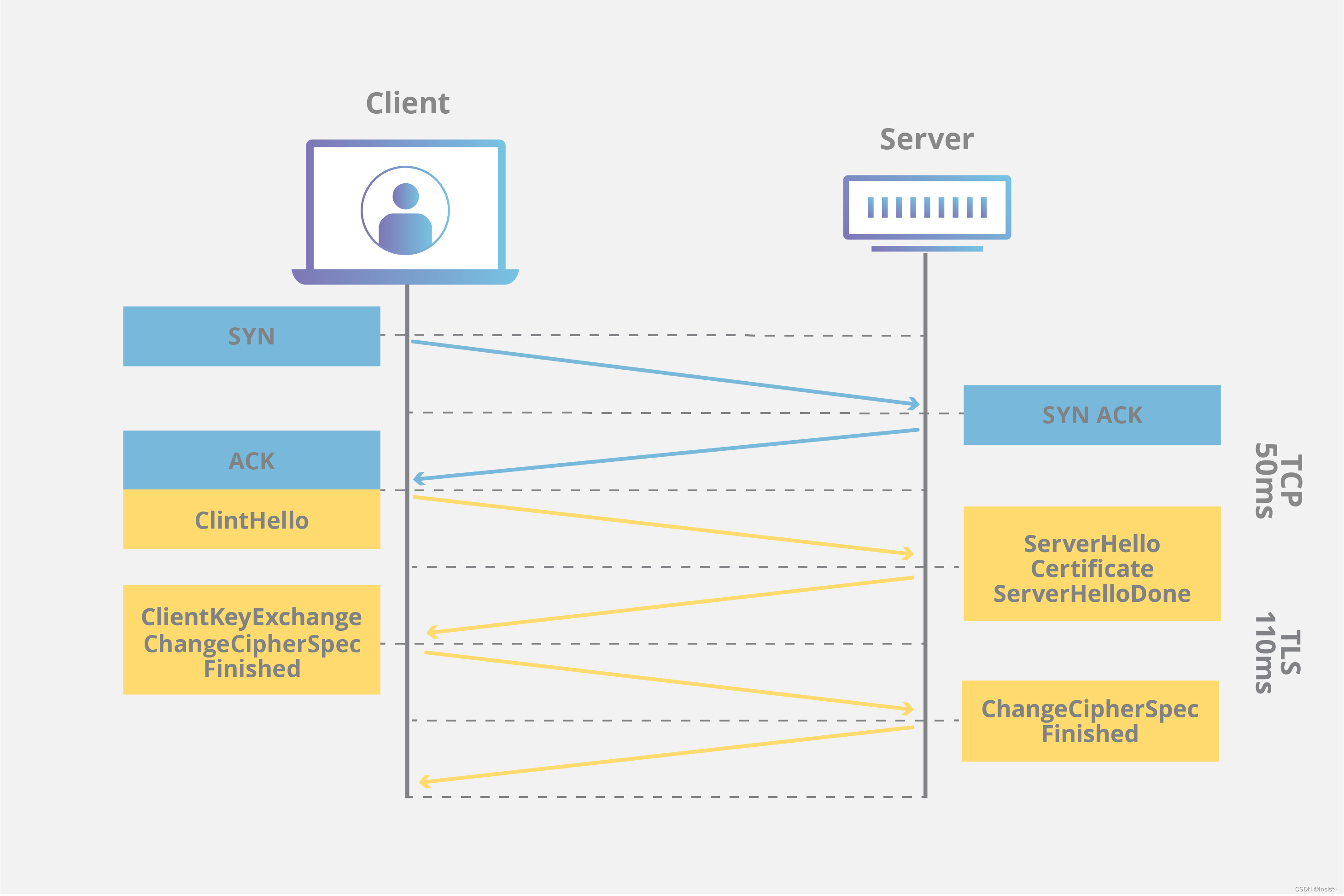
SSL/TLS协议的概念、工作原理、作用以及注意事项
个人主页:insist--个人主页 本文专栏:网络基础——带你走进网络世界 本专栏会持续更新网络基础知识,希望大家多多支持,让我们一起探索这个神奇而广阔的网络世界。 目录 一、SSL/TLS协议的基本概念 二、SSL/TLS的工作…...
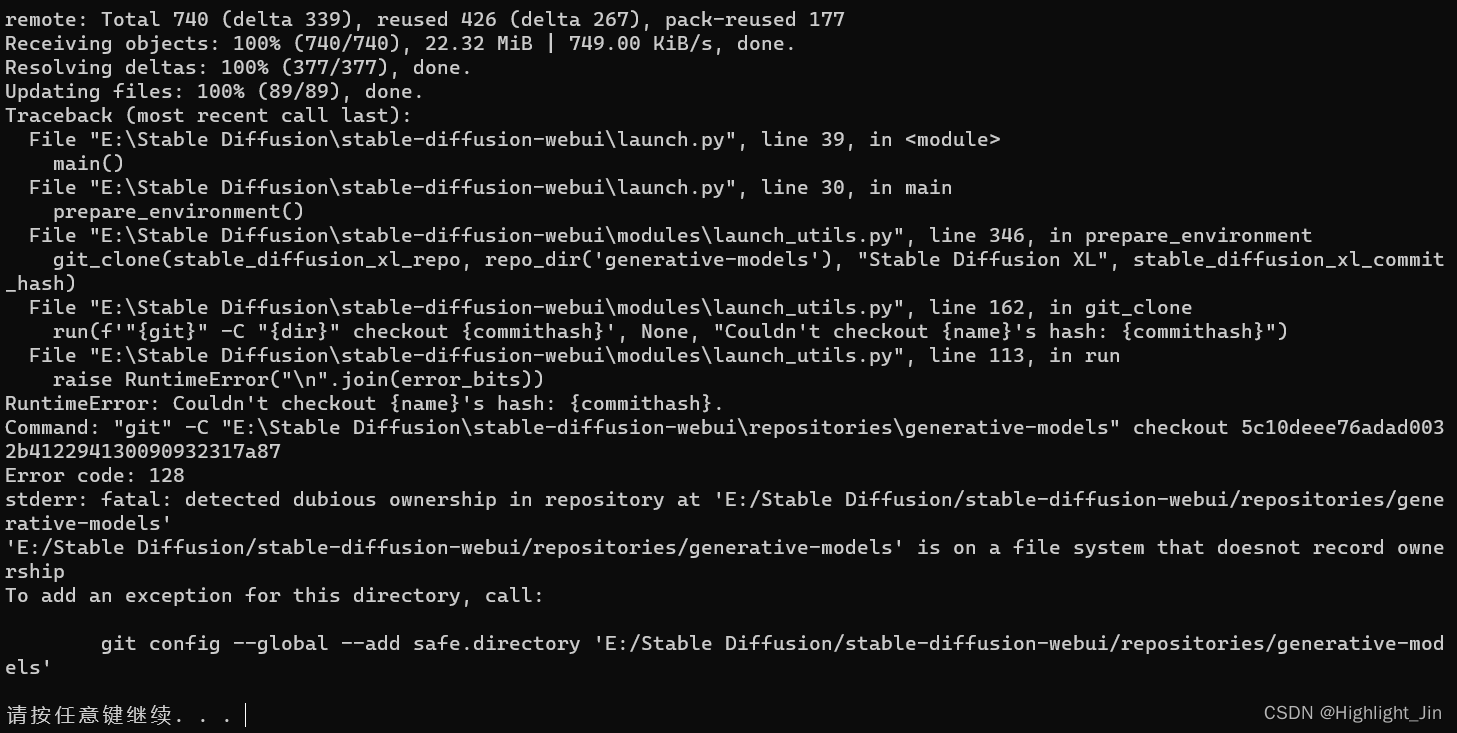
[Stable Diffusion教程] 第一课 原理解析+配置需求+应用安装+基本步骤
第一课 原理解析配置需求应用安装基本步骤 本次内容记录来源于B站的一个视频 以下是自己安装过程中整理的问题及解决方法: 问题:stable-diffusion-webui启动No Python at ‘C:\xxx\xxx\python.exe‘ 解答:打开webui.bat 把 if not de…...

uniapp结合Canvas+renderjs根据经纬度绘制轨迹(二)
uniapp结合Canvasrenderjs根据经纬度绘制轨迹 文章目录 uniapp结合Canvasrenderjs根据经纬度绘制轨迹效果图templaterenderjsjs数据结构 根据官方建议要想在 app-vue 流畅使用 Canvas 动画,需要使用 renderjs 技术,把操作canvas的js逻辑放到视图层运…...

VR全景加盟会遇到哪些问题?全景平台会提供什么?
想创业,你是否也遇到这些问题呢?我是外行怎么办?没有团队怎么办?项目回本周期快吗?项目靠谱吗?加盟平台可信吗?等等这类疑问。近几年,VR产业发展迅速,尤其是VR全景项目在…...

如何进行微服务的集成测试
集成测试的概念 说到集成测试,相信每个测试工程师并不陌生,它不是一个崭新的概念,通过维基百科定义可以知道它在传统软件测试中的含义。 Integration testing (sometimes called integration and testing, abbreviated I&T) is the pha…...

spark grpc 在master运行报错 exitcode13 User did not initialize spark context
程序使用sparksql 以及protobuf grpc ,执行报错 ApplicationMaster: Final app status: FAILED, exitCode: 13, (reason: Uncaught exception: java.lang.IllegalStateException: User did not initialize spark context! 先说原因 : 1.使用了不具备权限…...

nginx 反向代理的原理
Nginx(发音为"engine X")是一个高性能、轻量级的开源Web服务器和反向代理服务器。它的反向代理功能允许将客户端的请求转发到后端服务器,然后将后端服务器的响应返回给客户端。下面是Nginx反向代理的工作原理: 1.客户端…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
