php环境变量的配置步骤
要配置PHP的环境变量,以便在命令行中直接使用php命令,以下是一般的步骤:
Windows 操作系统
-
下载和安装PHP:首先,你需要从PHP官方网站(https://www.php.net/downloads.php)下载适用于你的操作系统的PHP安装程序,并按照指示进行安装。
-
找到PHP可执行文件路径:安装完成后,确定PHP可执行文件(
php.exe或php)的路径。在Windows上,默认情况下,它位于PHP安装目录的php文件夹中。 -
打开系统环境变量设置:在Windows上,右键点击"此电脑"(或“我的电脑”),选择"属性",然后点击"高级系统设置"。在弹出的窗口中,点击"环境变量"按钮。
-
配置系统环境变量:在"环境变量"窗口中,找到"系统变量"部分下的"Path"变量,并双击编辑它。
-
添加PHP路径到Path变量:在"编辑环境变量"窗口的"变量值"字段中,将PHP可执行文件的路径添加到现有的变量值之后,并用分号(
;)分隔。例如,如果PHP可执行文件路径是C:\php,那么你需要将C:\php添加到现有的变量值的末尾,之间用分号分隔。 -
保存和应用更改:完成路径的添加后,点击"确定"按钮分别关闭"编辑环境变量"窗口和"环境变量"窗口。
-
重启终端或命令提示符:在更改环境变量后,你需要重新启动已打开的终端或命令提示符窗口,以使更改生效。
-
检查PHP是否配置成功:重新打开一个命令提示符窗口,输入
php -v命令,如果能够正确显示PHP的版本信息,则表示配置成功。
完成上述步骤后,可以在命令行中直接使用php命令来执行PHP脚本了。请注意,不同的操作系统和安装配置可能会导致步骤的略微差异,这里提供的是一般的指导。
在配置 PHP 环境变量之前,您需要确保已经安装了 PHP,并且 PHP 可执行文件所在的目录具有可执行权限。以下是在不同操作系统上配置 PHP 环境变量的步骤:
Linux 操作系统:
打开终端。
使用文本编辑器(如 nano 或 vim)打开您的 bash 配置文件(通常是 ~/.bashrc 或 ~/.bash_profile)。
在文件的末尾添加以下行:
ruby
export PATH=$PATH:/path/to/php
将 /path/to/php 替换为您的 PHP 可执行文件所在的目录路径。 4. 保存并关闭文件。 5. 在终端中运行以下命令使配置生效:
bash
source ~/.bashrc
或者重新启动终端。
现在,您可以在终端中直接运行 php 命令来执行 PHP 文件。
macOS 操作系统:
打开终端。
使用文本编辑器(如 nano 或 vim)打开您的 bash 配置文件(通常是 ~/.bashrc 或 ~/.bash_profile)。
在文件的末尾添加以下行:
ruby
export PATH=$PATH:/path/to/php
将 /path/to/php 替换为您的 PHP 可执行文件所在的目录路径。 4. 保存并关闭文件。 5. 在终端中运行以下命令使配置生效:
bash
source ~/.bashrc
或者重新启动终端。
现在,您可以在终端中直接运行 php 命令来执行 PHP 文件。
这些步骤假设您已经正确安装了 PHP,并且 PHP 可执行文件位于正确的目录中。如果您在配置过程中遇到任何问题,请检查您的 PHP 安装和目录路径是否正确。
@漏刻有时
相关文章:

php环境变量的配置步骤
要配置PHP的环境变量,以便在命令行中直接使用php命令,以下是一般的步骤: Windows 操作系统 下载和安装PHP:首先,你需要从PHP官方网站(https://www.php.net/downloads.php)下载适用于你的操作系…...

Kdtree
Kdtree kdtree 就是在 n 维空间对数据点进行二分;具体先确定一个根,然后小于在这个维度上的根的节点在左边,大于的在右边,再进行下一个维度的划分。直到维度结束,再重复,或者直到达到了结束条件࿱…...
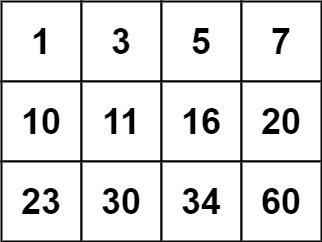
算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录 74. 搜索二维矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 74. 搜索二维矩阵: 给你一个满足下述两条属性的…...

element浅尝辄止7:InfiniteScroll 无限滚动
滚动加载:滚动至底部时,加载更多数据。 1.如何使用? //在要实现滚动加载的列表上上添加v-infinite-scroll,并赋值相应的加载方法, //可实现滚动到底部时自动执行加载方法。<template><ul class"infinit…...

Day05-Vue基础
Day05-Vue基础 一、单向数据流 父子组件通信。会在父组件中定义好数据,将数据传递给子组件,可以使用这个数据 Vue中针对props这个属性提出了一个单向数据流的概念。 Vue针对props做了一些限制,可以接受值,使用这个值,规范中不要去直接修改这个值 目的是为了对数据流进…...
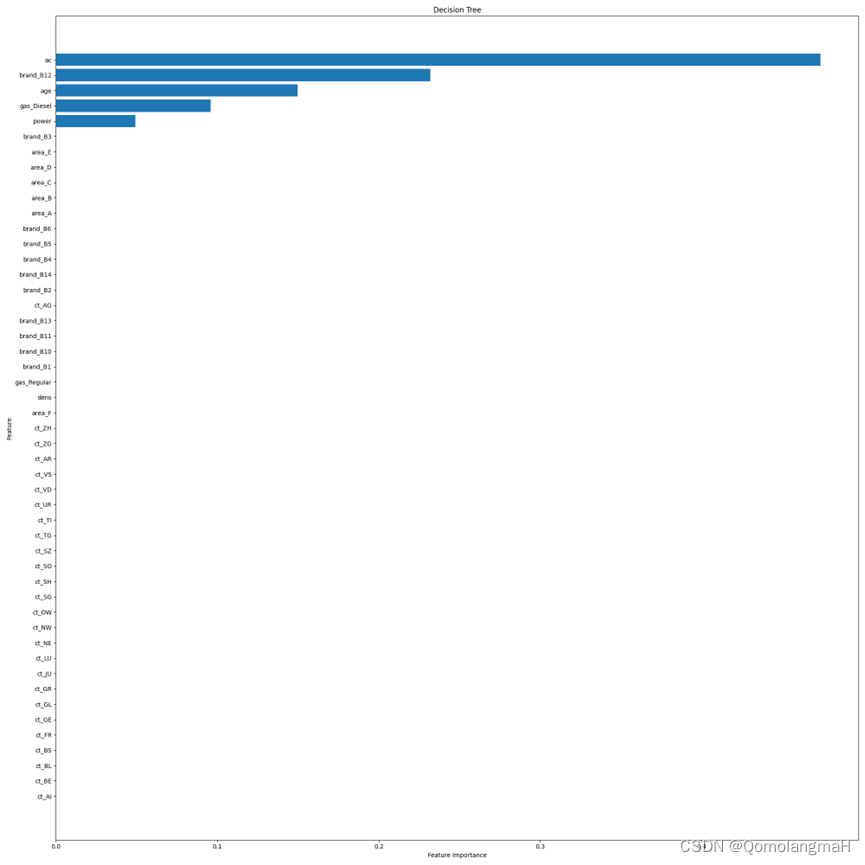
《机器学习在车险定价中的应用》实验报告
目录 一、实验题目 机器学习在车险定价中的应用 二、实验设置 1. 操作系统: 2. IDE: 3. python: 4. 库: 三、实验内容 实验前的猜想: 四、实验结果 1. 数据预处理及数据划分 独热编码处理结果(以…...
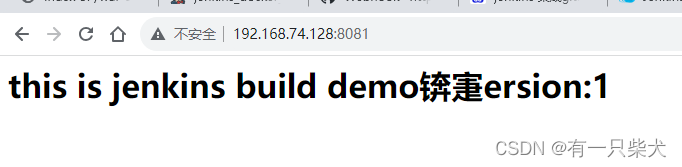
14. Docker中实现CI和CD
目录 1、前言 2、什么是CI/CD 3、部署Jenkins 3.1、下载Jenkins 3.2、启动Jenkins 3.3、访问Jenkins页面 4、Jenkins部署一个应用 5、Jenkins实现Docker应用的持续集成和部署 5.1、创建Dockerfile 5.2、集成Jenkins和Docker 6、小结 1、前言 持续集成(CI/CD)是一种…...

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
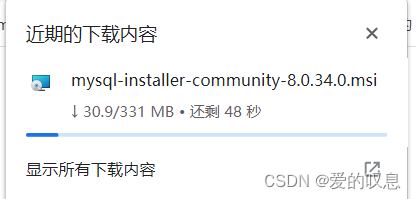
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
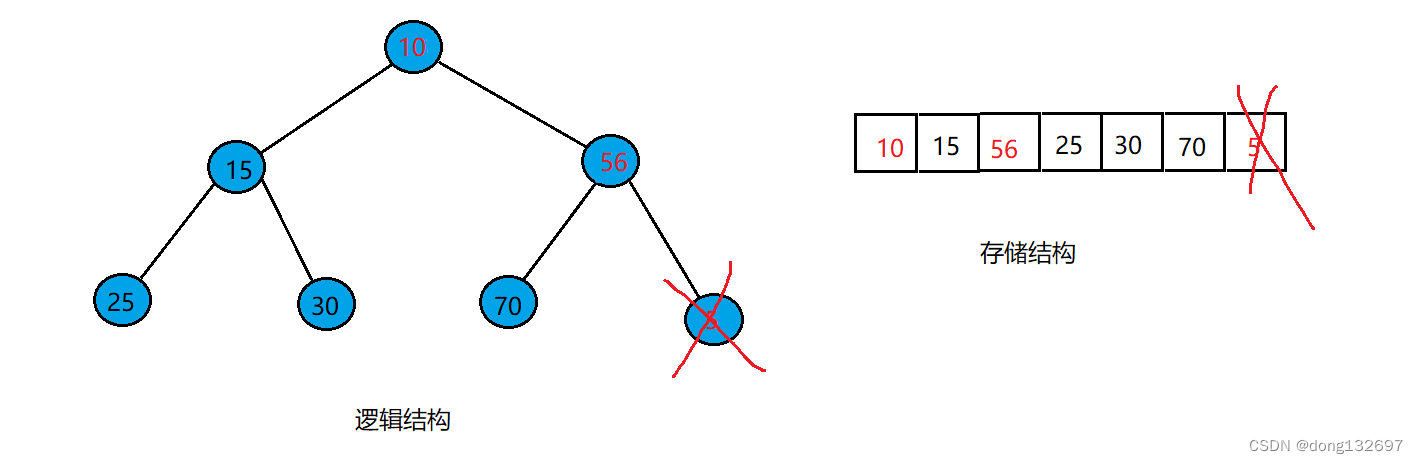
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...
)
前端优化页面加载速度的方法(持续更新)
提速方法方向 延迟脚本加载 使用 async 属性: 在这种方法中,脚本将在下载完成后立即执行,而不会阻塞其他页面资源的加载和渲染。这适用于那些不依赖于其他脚本和页面内容的脚本,例如分析脚本等。示例如下: html …...

利用SSL证书的SNI特性建立自己的爬虫ip服务器
今天我要和大家分享一个关于自建多域名HTTPS爬虫ip服务器的知识,让你的爬虫ip服务器更加强大!无论是用于数据抓取、反爬虫还是网络调试,自建一个支持多个域名的HTTPS爬虫ip服务器都是非常有价值的。本文将详细介绍如何利用SSL证书的SNI&#…...

HTML和CSS
HTML HTML(Hyper Text Markup Language):超文本语言 超文本:超越了文本的限制,比普通文本更强大。除了文字信息,还可以定义图片、音频、视频等内容。 标记语言:由标签构成的语言 HTML标签都是预定义好的。例如:使用&l…...

C#的IndexOf
在 C# 中,IndexOf 是一个字符串、数组或列表的方法,用于查找指定元素的第一个匹配项的索引。它返回一个整数值,表示匹配项在集合中的位置,如果未找到匹配项,则返回 -1。 IndexOf 方法有多个重载形式,可以根…...

深度学习2.神经网络、机器学习、人工智能
目录 深度学习、神经网络、机器学习、人工智能的关系 大白话解释深度学习 传统机器学习 VS 深度学习 深度学习的优缺点 4种典型的深度学习算法 卷积神经网络 – CNN 循环神经网络 – RNN 生成对抗网络 – GANs 深度强化学习 – RL 总结 深度学习 深度学习、神经网络…...

利用LLM模型微调的短课程;钉钉宣布开放智能化底座能力
🦉 AI新闻 🚀 钉钉宣布开放智能化底座能力AI PaaS,推动企业数智化转型发展 摘要:钉钉在生态大会上宣布开放智能化底座能力AI PaaS,与生态伙伴探寻企业服务的新发展道路。AI PaaS结合5G、云计算和人工智能技术的普及和…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
