【leetcode 力扣刷题】字符串匹配之经典的KMP!!!
字符串子串匹配相关
- 28. 找出字符串中第一个匹配项的下标
- 暴力求解
- KMP
- 459. 重复的子字符串
- 暴力求解
- 在S+S中找S
以下是能用KMP求解的算法题,KMP是用于字符串匹配的经典算法【至今没学懂………啊啊啊】
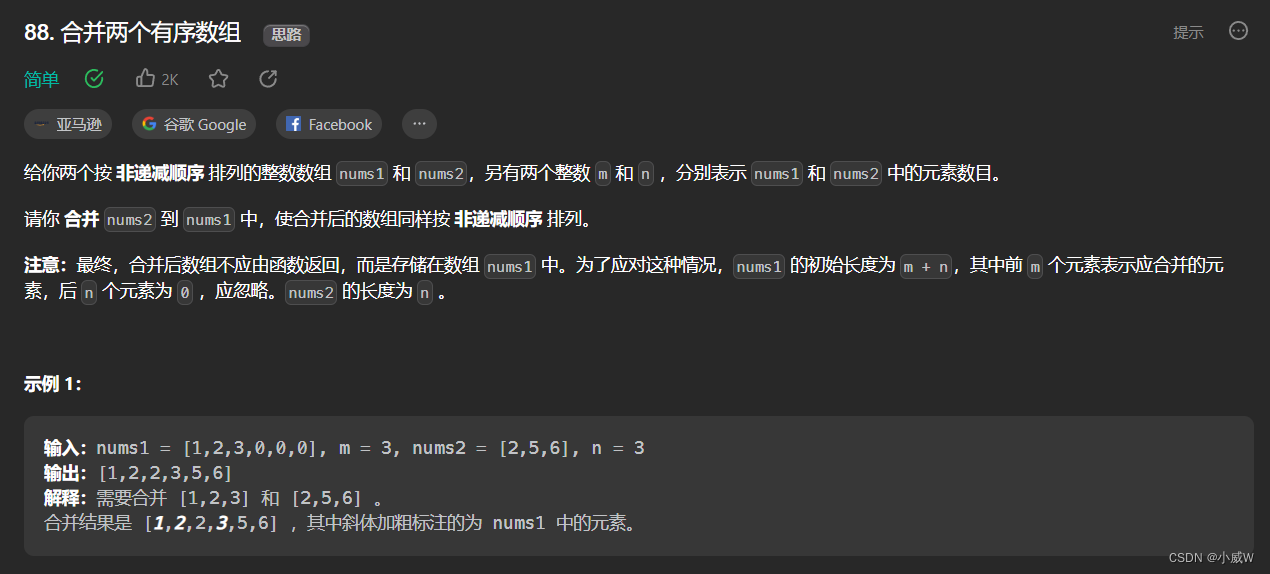
28. 找出字符串中第一个匹配项的下标
题目链接:28. 找出字符串中第一个匹配项的下标
题目内容:

题意还是很好理解的,要在字符串haystack中查找一个完整的needle,即字符串匹配。
暴力求解
暴力求解就是用两层循环:haystack从第i个字符开始,needle从第一个字符开始j = 0,之后依次判断needle[j]和haystack[j+i]是否相等。如果不相等,说明haystack中从第i位开始的子串和needle是不匹配的。之后j要回溯到j = 0,i向后移动一位。代码实现(C++):
class Solution {
public:int strStr(string haystack, string needle) {//haystack下标最大值int n = haystack.size() - needle.size();//外层是haystack从下标i开始和needle逐字符比较for(int i = 0 ; i <= n; i++){int j = 0;//needle从j=0开始while( j < needle.size()){//如果有相等就退出循环,开启下一轮if(haystack[j+i] != needle[j])break;j++;}//如果是遍历完needle都与从i开始的子串相同,就找到了if(j == needle.size())return i;}return -1;}
};
KMP
暴力求解中,如果当前的needle[j]和haystack[j+i]不匹配,needle中j会回退到0,haystack中i+j回退到i+1,这里是可以优化的,KMP就是为了减少这样的回溯。
KMP是用于求解字符串匹配的算法,在当前needle[j]和haystack[j+i]不匹配时,能够快速找到j应该移动到的位置,而不是直接回溯到开头。比如下面图中s[i]和p[j]不匹配后,由于p[j]前面的子串的前缀ab和后缀ab相同,因此j不需要回溯到0,是移动到abc中c的位置,继续和s[i]比较。

KMP中一个重点是最长相同前后缀长度。什么是前缀:一个字符串从第一个字符开始的,不包括最后一个字符的子串;什么是后缀:一个字符串中从最后一个字符开始的,不包括第一个字符的子串。
最长相同前后缀长度,就是一个字符串中相同的前后缀里面,最长的一组的长度。比如下图里对于ababa这个字符串,相同前后缀有两组,但是我们需要最长那组的长度。因为字符串匹配过程中,S[i]和P[j]不匹配时,j是要根据P[j]前面子串的前后缀长度来回退的,选择最长前后缀能够保证不遗漏答案。

KMP算法需要求模式串P的next数组,实际上这个next数组记录的就是P所有从第一个字符开始的子串的最长相同前后缀的长度:next[i]表示下标0到下标i这段子串的,最长相同前后缀的长度。假设有next[i-1]=m,那么next[i] <= next[i-1]+1,其中取等需要P[next[i-1]] == P[i]。【因为next[i-1]里面存的是长度,当作下标的时候就是最长相同前后缀里面那个前缀后面一个字符;而P[i]就是P[i-1]最长相同前后缀的后缀的后后面一个字符】。

如果P[next[i-1]] != P[i],那么就要判断P[next[next[i-1]-1]]和P[i]的关系,直到下标回溯到0或者找到了和P[i]匹配的位置。
代码如下(C++):
ector<int> Kmp_Next(string s){int n = s.size();vector<int> next(n, 0);//next数组中存的是对应下标处子串【包括下标位置】的最长前后缀的长度next[0] = 0;for(int i = 1; i < n; i++){int j = next[i-1];while(j>0 && s[j] != s[i]) //不匹配就循环回退j = next[j-1];if(s[i] == s[j]) //如果匹配,长度在j的基础上+1j++;next[i] = j;}return next;
}
KMP的匹配过程:首先求得了模式串P的next数组,即每个P[0]~P[i]这一段这串中最长的相同前后缀的长度;然后P中的字符从P[j=0]开始,S中的字符也从S[pos=0]开始,判断S[pos]和P[j]是否匹配,如果匹配就j++,pos++向后移动;如果不匹配,j就根据next[j-1]回退,并判断回退后新的下标j对应的P[j]和S[pos]是否匹配,如果不匹配继续回退,直到匹配或者j=0。实现过程如下:
- 要先找到P中哪个字符和当前的S[pos]匹配。因为如果P[j] != S[pos],j需要根据next数组循环回退j = next[j-1],那么就先找到能够匹配的j,才停止;
while(j>0 && haystack[pos] != needle[j])j = next[j-1];
- 上面循环退出有两种情况,P[j] == S[pos]或者j == 0;如果是前者,自然pos++,j++;如果是后者,就只有pos++;
if(haystack[pos] == needle[j]){pos++;j++;}
elsepos++;
- 最后停止要么是j遍历到了最后,要么是pos遍历到了最后。只有j遍历到最后才算完全匹配;
完整代码如下(C++):
class Solution {
public://先求needle的next数组vector<int> Kmp_Next(string s){int n = s.size();vector<int> next(n, 0);//next数组中存的是对应下标处子串【包括下标位置】的最长前后缀的长度next[0] = 0;for(int i = 1; i < n; i++){int j = next[i-1];while(j>0 && s[j] != s[i])j = next[j-1];if(s[i] == s[j])j++;next[i] = j;}return next; }int strStr(string haystack, string needle) {vector<int> next = Kmp_Next(needle);int pos = 0, j = 0;//kmp匹配过程while(j < needle.size() && pos < haystack.size()){while(j>0 && haystack[pos] != needle[j])j = next[j-1];if(haystack[pos] == needle[j]){pos++;j++;} elsepos++; }//needle没有遍历完,pos已经遍历完haystack了,没有匹配的地方if(j < needle.size())return -1;//needle遍历完,有匹配的地方elsereturn pos - needle.size();}
};
459. 重复的子字符串
题目链接:459. 重复的子字符串
题目内容:

暴力求解
题目要求我们判断字符串S是不是由其某个子串重复构成的。假设子串m能够重复构成S,那么S可以表示m/mm/m/……这样的形式,即由n个m组成【n≥2】。分析这样的子串有两个特点:
- 从第一个字符开始;
- 长度≤S.size()/2;
- S.size()一定能够被m.size()整除;
根据子串的这两个特点,我们可以去判断所有这样的子串,子串长度从1开始,最多有S.size()/2这么多个。针对每个子串,先判断其长度能否整除S的长度;再判断其能否重复构成S——将S分成和子串m一样长度的k个子串,所有的子串和m对比是否一样,如果有一个不一样就直接break。
代码如下(C++):
class Solution {
public:bool repeatedSubstringPattern(string s) {int size = s.size();//end是子串m的长度for(int end = 1; end <= size/2; end++ ){//s长度能够被end整除才继续下面的判断if(size % end == 0){int i;//剩下的子串和m对比for(i = end ; i < size ; i += end ){if(s.substr(0,end) != s.substr(i, end))break;}if(i == size )return true;} }return false;}
};
暴力求解的时间复杂度是O(n^2)。
在S+S中找S
假设S由n个子串m组成【n≥2】,那么S+S中有2n个m,将S+S去头去尾【删除第一个和最后一个元素就能实现去掉一个m和最后一个m】后还有2n-2个m,由于n≥2,2n-2≥n。那么如果S+S去头去尾后还能有至少一个完整的S,就能证明其是由m循环组成的。代码实现(C++)【就一句话】:
class Solution {
public:bool repeatedSubstringPattern(string s) {return (s+s).find(s,1) != s.size() ? true : false;}
};
那么如果不是由子串m循环组成的字符串,S+S去头去尾以后一定找不到一个完整的S吗?【emm需要再研究一下】
相关文章:

【leetcode 力扣刷题】字符串匹配之经典的KMP!!!
字符串子串匹配相关 28. 找出字符串中第一个匹配项的下标暴力求解KMP 459. 重复的子字符串暴力求解在SS中找S 以下是能用KMP求解的算法题,KMP是用于字符串匹配的经典算法【至今没学懂………啊啊啊】 28. 找出字符串中第一个匹配项的下标 题目链接:28. 找…...

C#的反射机制
介绍 当谈到C#的反射机制时,它提供了一种动态地在运行时获取和操作类型信息的能力。通过反射,可以在编译时未知的情况下,使用类型信息来创建对象、调用方法、访问属性和字段等。下面是一些反射机制的重要概念和用法: Type 类型&a…...

浅谈城市轨道交通视频监控与AI视频智能分析解决方案
一、背景分析 地铁作为重要的公共场所交通枢纽,流动性非常高、人员大量聚集,轨道交通需要利用视频监控系统来实现全程、全方位的安全防范,这也是保证地铁行车组织和安全的重要手段。调度员和车站值班员通过系统监管列车运行、客流情况、变电…...
【LeetCode每日一题合集】2023.8.14-2023.8.20(⭐切披萨3n块披萨)
文章目录 617. 合并二叉树833. 字符串中的查找与替换(模拟)2682. 找出转圈游戏输家(模拟)1444. 切披萨的方案数(⭐⭐⭐⭐⭐)解法——从递归到递推到优化(二维前缀和记忆化搜索) 1388…...

通过ref 操作dom , 点击按钮后跳转到页面指定图片位置
滚动图片到视图 定义了一个名为 scrollToIndex 的函数,它接受一个参数 index。当按钮被点击时,这个函数会被调用,并根据传入的 index 值来滚动到对应的图片。 以 alt 来标记图片位置 alt“Tom” import { useRef } from "react";c…...
QT 设置应用程序图标
1.下载xx.ico图标:ico网址 2.在线PNG转换ICO:png在线转换ico 3.添加图标资源 1)新建文件路径 2)添加图片资源 3)在 .pro文件里面添加图片 4)将xx.ico放到工程目录,编译完可以看到xx.exe的图标…...
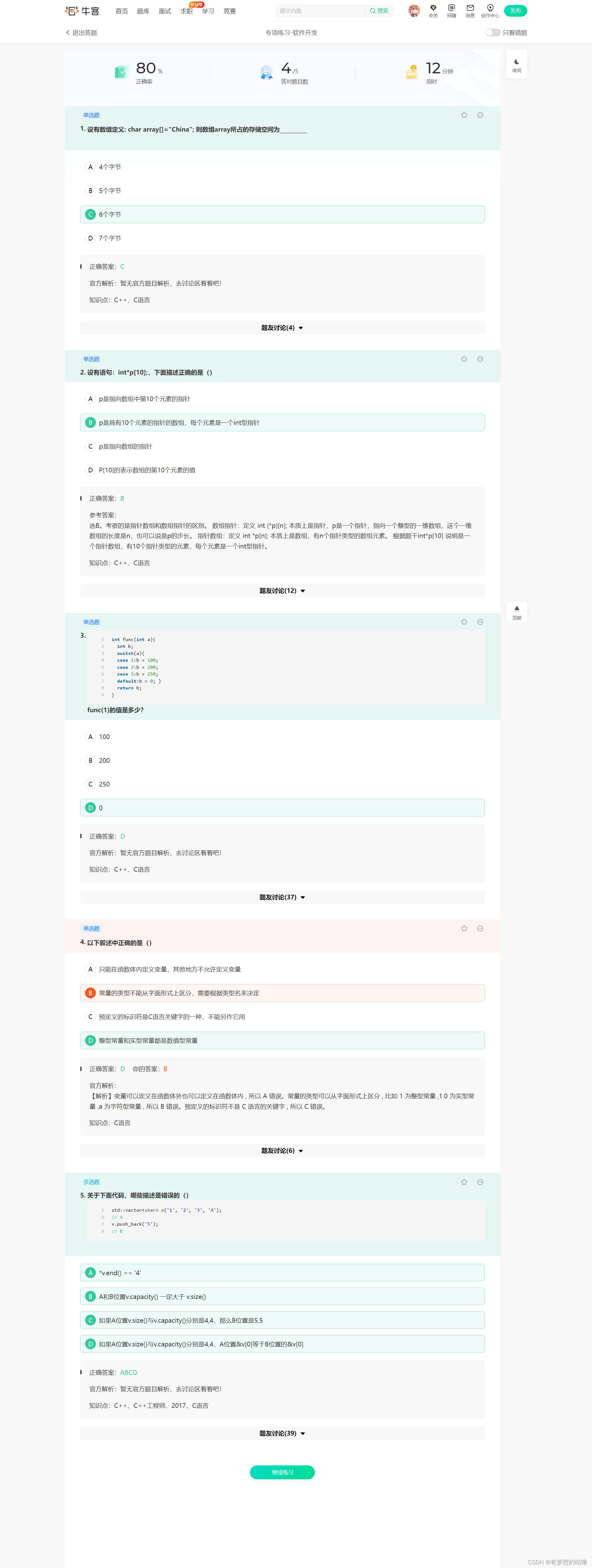
牛客网刷题
牛客网刷题-C&C 2023年9月3日15:58:392023年9月3日16:37:01 2023年9月3日15:58:39 2023年9月3日16:37:01 整型常量和实型常量的区别...
ES6核心语法
主要记录学习ES6的语法 1、let和const 同es5中的var来声明变量。三者的区别分别是: var声明的变量存在变量提升,先声明未赋值,值为undefined。且变量声明可在函数块内使用。变量声明之后可以重复声明let声明的变量无变量提升。作用域是块级…...

python 之import与from import 导入库的解析与差异
文章目录 1. **使用import导入整个模块**:2. **使用from import导入特定内容**:注意事项别名的使用 在Python中,import和from import是用于导入模块中内容的两种不同方式。下面详细介绍它们的用法和差异: 1. 使用import导入整个模…...
python实现MQTT协议(发布者,订阅者,topic)
python实现MQTT协议 一、简介 1.1 概述 本文章针对物联网MQTT协议完成python实现 1.2 环境 Apache-apollo创建brokerPython实现发布者和订阅者 1.3 内容 MQTT协议架构说明 : 利用仿真服务体会 MQTT协议 针对MQTT协议进行测试 任务1:MQTT协议应…...

2023年09月03日-----16:58
协同过滤推荐和矩阵分解本质上有什么不同?协同过滤推荐和矩阵分解是两种推荐系统方法,它们在某些方面有相似之处,但也有一些本质不同之处。 基本原理: 协同过滤推荐:协同过滤是一种基于用户行为数据的推荐方法,它依赖于用户-物品交互数据,如用户的评分或点击历史。协同过…...
HTTP状态码504(Gateway Timeout)报错原因分析和解决办法
文章目录 504报错原因分析一、用户角度1. 代理服务器问题2. 网络问题 二、网站管理员角度1. 服务器负载过重2. 网关配置问题3. 目标服务器响应慢4. IIS/nginx/apache服务关闭5. 维护或故障6. 数据库的慢处理也会导致504 用户角度可以采取哪些措施解决504错误1. 刷新页面2. 检查…...
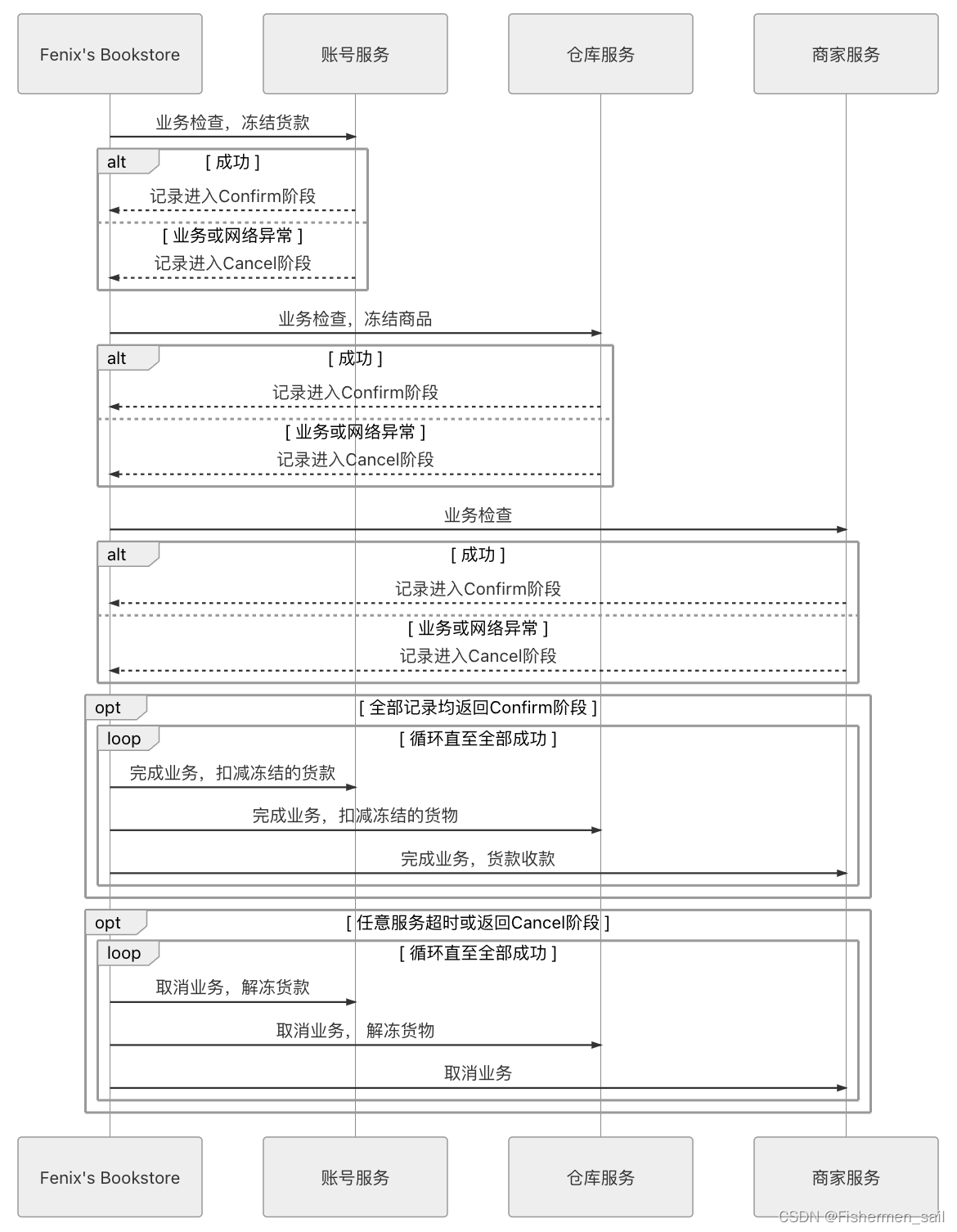
《凤凰架构》第三章——事务处理
前言 由于一些地方原文感觉不太清楚,有些地方用小林coding的文章代替。 总结 事务处理主要的目的就是要让数据在各种条件下,最终的运行结果都能符合你的期望。要达成这个目标有三点需要满足:原子性(业务要么同时成功࿰…...

音视频添 加水印
一、文字水印 在视频中增加文字水印需要准备的条件比较多,需要有文字字库处理的相关文件,在编译FFmpeg时需要支持FreeType、FontConfig、iconv,系统中需要有相关的字库,在FFmpeg中增加纯字母水印可以使用drawtext滤镜进行支持&am…...

使用Python的requests库与chatGPT进行通信
前言 在人工智能领域,自然语言处理模型如OpenAI GPT-3.5 Turbo具有广泛的应用。虽然官方提供了Python库来与这些模型进行交互,但也有一些人更喜欢使用requests库来自定义请求和处理响应,比如现在很多第三方LLM都提供了与chatGPT类似的http请…...

SASS常用内置函数
1,math 引入:use "sass:math"; 常用函数: ceil($number) - 向上取整floor($number) - 向下取整round($number) - 四舍五入max($number...) - 比较若干数值并取最大值min($number...) - 比较若干数值并取最小值random() - 取0~1之…...

2023年05月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:怪盗基德的滑翔翼 怪盗基德是一个充满传奇色彩的怪盗,专门以珠宝为目标的超级盗窃犯。而他最为突出的地方,就是他每次都能逃脱中村警部的重重围堵,而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。 有一天,怪盗基德像往…...
Emmet 使用笔记小结
Emmet 使用笔记小结 最近在跟视频走 CSS 的教程,然后要写很多的 HTML 结构,就想着总结一下 Emmet 的语法。 Emmet 是一个工具可以用来加速 HTML 和 CSS 的开发过程,不过 emmet 只支持 HTML & XML 文件结构,所以我个人觉得对…...

如何使用Puppeteer进行新闻网站数据抓取和聚合
导语 Puppeteer是一个基于Node.js的库,它提供了一个高级的API来控制Chrome或Chromium浏览器。通过Puppeteer,我们可以实现各种自动化任务,如网页截图、PDF生成、表单填写、网络监控等。本文将介绍如何使用Puppeteer进行新闻网站数据抓取和聚…...
【LeetCode每日一题合集】2023.8.7-2023.8.13(动态规划分治)
文章目录 344. 反转字符串1749. 任意子数组和的绝对值的最大值(最大子数组和)1281. 整数的各位积和之差1289. 下降路径最小和 II解法1——动态规划 O ( n 3 ) O(n^3) O(n3)解法2——转移过程优化 O ( n 2 ) O(n^2) O(n2) ⭐ 1572. 矩阵对角线元素的和解法…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
