VHDL语言基础-时序逻辑电路-计数器
目录
计数器的设计:
计数器的作用:
计数器的实现:
1、用“+”函数描述:
用T触发器级联构成的串行进位的二进制加法计数器的仿真波形:
计数器的仿真:
计数器的设计:
计数是一种最简单基本的运算,计数器就是实现这种运算的逻辑电路
计数器的作用:
主要是对脉冲的个数进行技术,以实现测量、计数和控制的功能,同时兼有分频功能。比如七位计数器,可对输入时钟进行七分频。

计数器的实现:
1、用“+”函数描述:
Library ieee ;
Use ieee.std_logic_1164.all;
Use ieee.std_logic_unsigned.all;
Entity counter is
generic( n: natural :=4);
port ( clk : in std_logic;
reset : in std_logic ;
count : out std_logic_vector(n-1 downto 0) );
End counter;
architecture ripple of counter is
component T_FF is
port( T : in std_logic ;
clk:in std_logic;
reset:in std_logic;
Q : out std_logic;
Qbar:out std_logic);
end component ; --将前面描述好的T触发器定义为元件;
signal carry: std_logic_vector( n downto 0);
Begin
carry(0)<=clk;
g0: for i in 0 to n-1 generate --循环
T1: T_FF port map ( ‘1’, carry( i ), reset, count( i ), carry( i+1 ) );
end generate g0;
End ripple ;
上例程序中的循环:
g0: for i in 0 to n-1 generate --循环
T1: T_FF port map ( ‘1’, carry( i ), reset, count( i ), carry( i+1 ) );
可以分解成:
T0: T_FF port map ( ‘1’, carry( 0 ), reset, count( 0 ), carry(1 ) );
T1: T_FF port map ( ‘1’, carry( 1 ), reset, count( 1 ), carry( 2 ) );
T2: T_FF port map ( ‘1’, carry( 2 ), reset, count( 2 ), carry( 3 ) );
T3: T_FF port map ( ‘1’, carry( 3 ), reset, count( 3 ), carry( 4 ) );
…………………………
…………………………
Tn-1: T_FF port map ( ‘1’, carry( n-1 ), reset, count( n-1 ), co );
用T触发器级联构成的串行进位的二进制加法计数器的仿真波形:

注意:这里我们可以发现在奇数变为偶数的时候有一个小小的变化。
计数器的仿真:
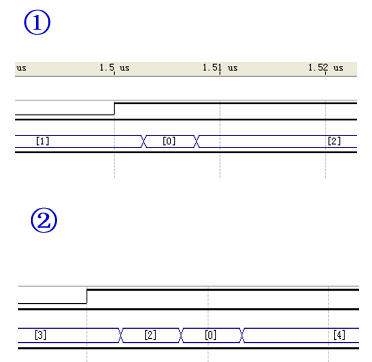
信号赋值的时候有延迟,在计数器由001变为010的时候,先是由
count(0)<=0;carry(1)<=1; -第一步
count(1)<=1;
所以count会先变为000,接着延迟一段时间后才变为010。
同理,对于011变为100的时候,有:
count(0)<=0;carry(1)<=1; -第一步
count(1)<=0;carry(2)<=1; -第二步
count(2)<=1; -第三步
故从011变为010,再变为100。
相关文章:

VHDL语言基础-时序逻辑电路-计数器
目录 计数器的设计: 计数器的作用: 计数器的实现: 1、用“”函数描述: 用T触发器级联构成的串行进位的二进制加法计数器的仿真波形: 计数器的仿真: 计数器的设计: 计数是一种最简单基本的…...
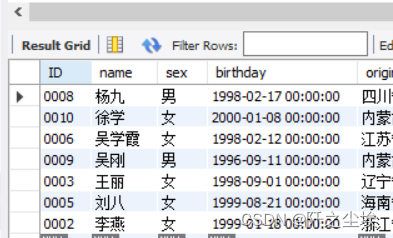
MySQL数据库07——高级条件查询
前面一章介绍了基础的一个条件的查询,如果多条件,涉及到逻辑运算,and or 之类的。就是高级一点的条件查询。本章来介绍复杂的条件搜索表达式。 AND运算符 AND运算符只有当两边操作数均为True时,最后结果才为True。人们使用AND描述…...

《Terraform 101 从入门到实践》 第四章 States状态管理
《Terraform 101 从入门到实践》这本小册在南瓜慢说官方网站和GitHub两个地方同步更新,书中的示例代码也是放在GitHub上,方便大家参考查看。 军书十二卷,卷卷有爷名。 为什么需要状态管理 Terraform的主要作用是管理云平台上的资源ÿ…...
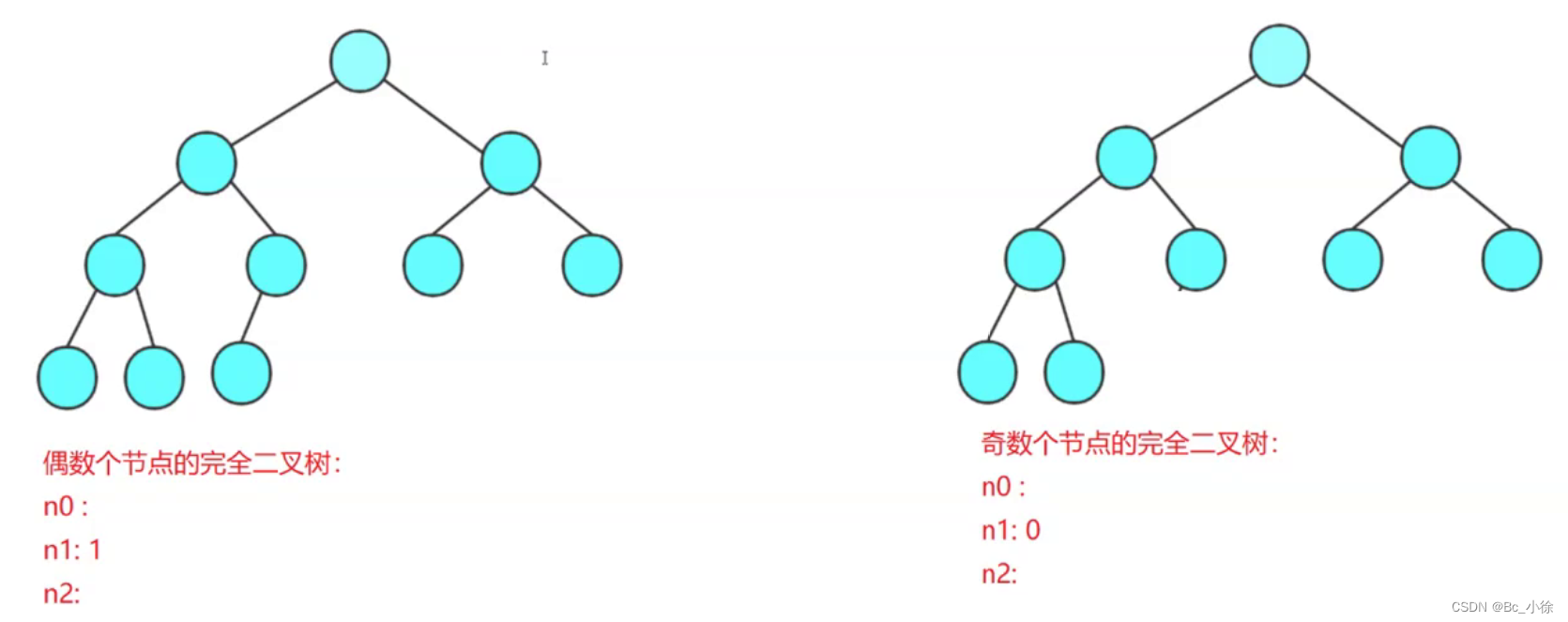
数据结构之二叉树
🎈一.二叉树相关概念 1.树 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合,树结构通常用来存储逻辑关系为 "一对多" 的数据。例如: 关于树的几个重要概念&…...
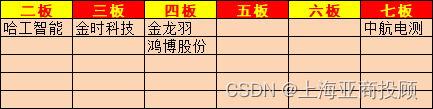
上海亚商投顾:三大指数集体调整 消费板块逆市活跃
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。市场情绪三大指数今日集体调整,沪指全天弱势震荡,创业板指盘中跌超1%。旅游、食品、乳业等大消费板块…...
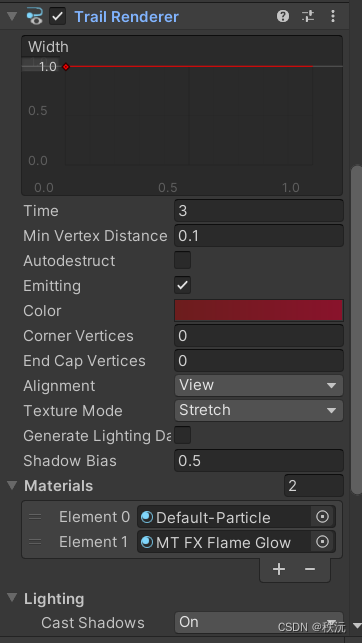
【2023unity游戏制作-mango的冒险】-开始画面API制作
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:游戏制作 ⭐mango的冒险-开始画面制作⭐ 文章目录⭐mango的冒险-开始画面制作⭐👨&…...

【微服务】Nacos配置管理
🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 Nacos除了可以做配置管理,同样可以当作注册中心来使用。 了解注册中心用法点击跳转👉【微服务】Nacos注册中心 一.引入 当微服务部署的实例越来越多࿰…...
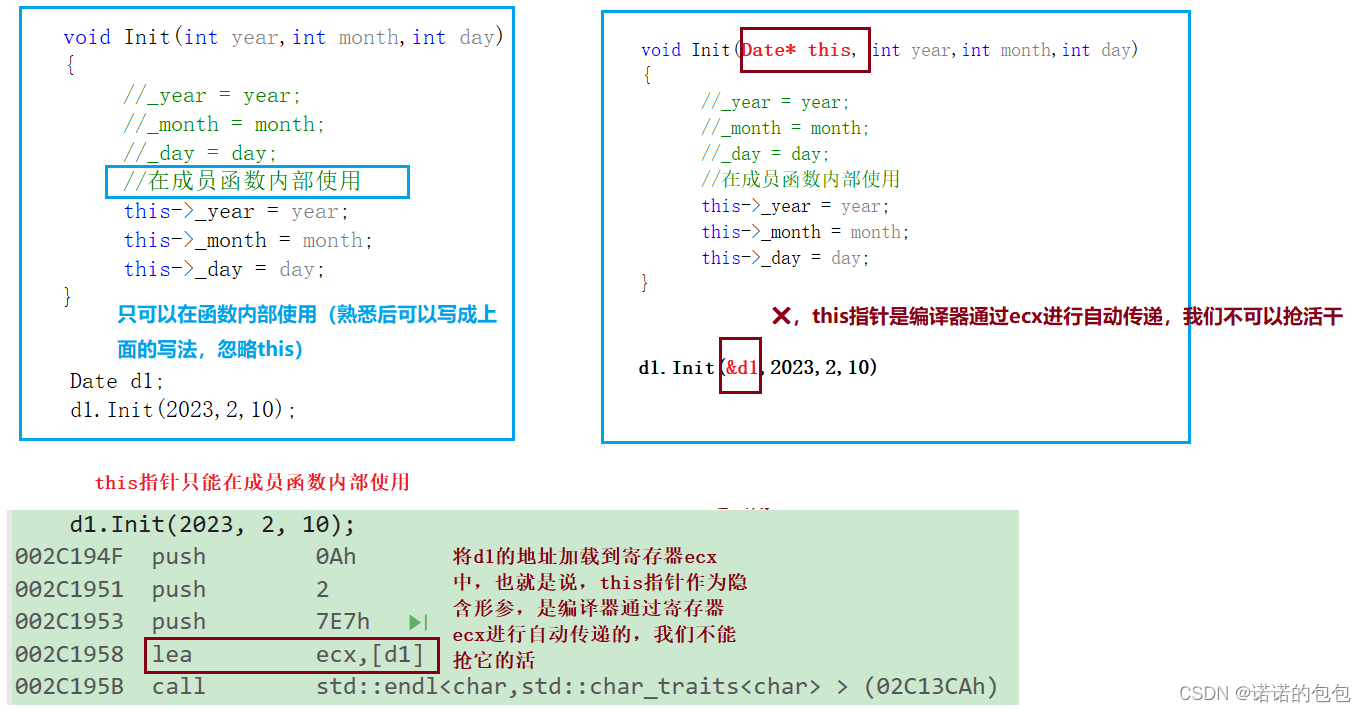
【C++】类与对象理解和学习(上)
专栏放在【C知识总结】,会持续更新,期待支持🌹类是什么?类是对对象进行描述的,是一个模型一样的东西,限定了类有哪些成员,定义出一个类并没有分配实际的内存空间来存储它(实例化后才…...
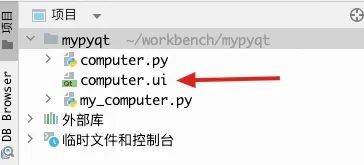
Pyqt5小案例,界面与逻辑分离的小计算器程序
直接看下最终效果: 使用技术总结 使用Designer设计界面 使用pyuic5命令导出到python文件 新建逻辑处理文件,继承pyuic5导出的文件的类,在里面编写信号与槽的处理逻辑 使用Designer设计界面 要使用Designer,安装一个Python库即…...

leaflet加载KML文件,显示图形(方法2)
第049个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中加载KML文件,将图形显示在地图上。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果; 注意如果OpenStreetMap无法加载,请加载其他来练习 文章目录 示例效果配置方式示例源代码(共66…...

Mysql 部署 MGR 集群
0. 参考文章 官方文档: MySQL :: MySQL 8.0 Reference Manual :: 18.2 Getting Started 博客: MGR 单主模式部署教程(基于 MySQL 8.0.28) - 墨天轮 (modb.pro) mysql MGR单主模式的搭建 - 墨天轮 (modb.pro) MySQL 5.7 基于…...

迁移至其他美国主机商时需要考虑的因素
网站的可访问性是关系业务的关键因素之一。一个稳定、快速且优化良好的主机上的网站更有可能享受不间断的流量,并在谷歌的SERP中获得更好的排名。因此,在构建企业网站时,选择合适的主机商相当重要。不过就以美国主机为例,由于每个…...

【数据结构】第二章 线性表
文章目录第二章 知识体系2.1 线性表的定义和基本操作2.1.1 线性表的定义2.1.2 线性表的基本操作2.2 线性表的顺序表示2.2.1 顺序表的定义2.2.2 顺序表的基本操作的实现2.3 线性表的链式表示2.3.1 单链表的定义2.3.2 单链表的基本操作实现2.3.3 双链表2.3.4 循环链表2.3.5 静态链…...
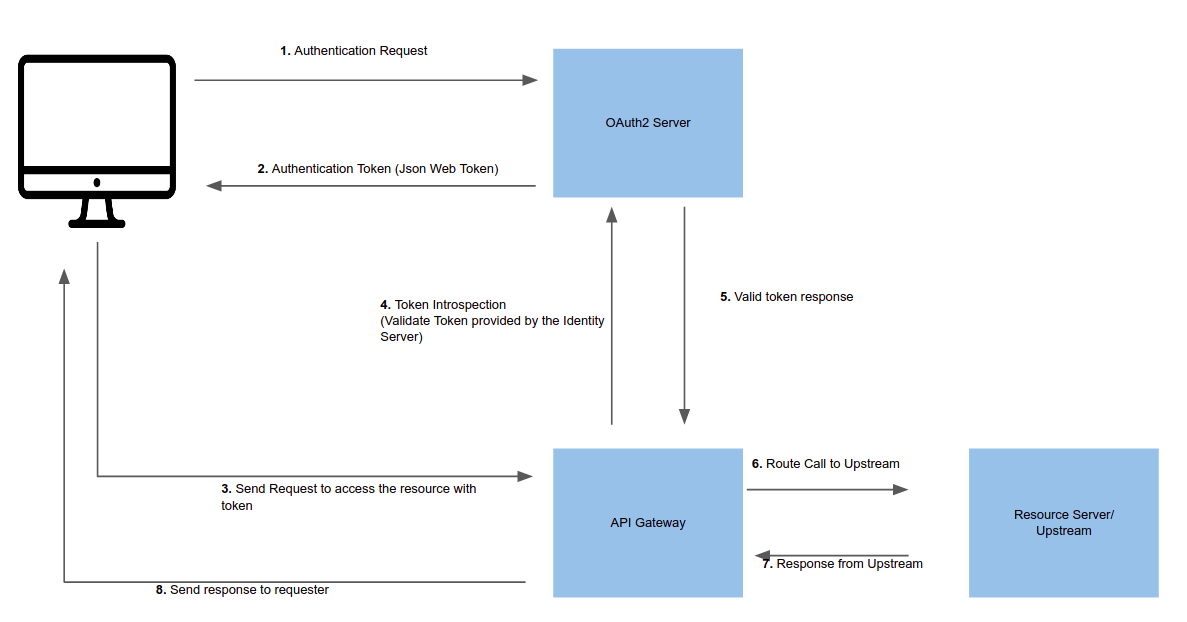
RESTful API 为何成为顶流 API 架构风格?
作者孙毅,API7.ai 技术工程师,Apache APISIX Committer 万物互联的世界充满着各式各样的 API ,如何统筹规范 API 至关重要。RESTful API 是目前世界上最流行的 API 架构风格之一,它可以帮助你实现客户端与服务端关注点分离&#x…...
)
Python基础知识点汇总(列表)
列表的含义 列表由一系列按特定顺序排列的元素组成,是Python中内置的可变序列。 **注:**列表的所有元素放在中括号[]中,相邻的两个元素用逗号分隔; 可将整数、实数、字符串、列表、元组等任何类型的内容放到列表中,且同一列表的元素类型可以不同。 列表的创建和删除 1.…...
新的一年软件测试行业的趋势能够更好?
如果说,2022年对于全世界来说,都是一场极大的挑战的话;那么,2023年绝对是机遇多多的一年。众所周知,随着疫情在全球范围内逐步得到控制,无论是国际还是国内的环境,都会呈现逐步回升的趋势&#…...

Threejs中的Shadow Mapping(阴影贴图)
简而言之,步骤如下: 1.从灯光位置视点(阴影相机)创建深度图。 2.从相机的位置角度进行屏幕渲染,在每个像素点,比较由阴影相机的MVP矩阵计算的深度值和深度图的值的大小,如果深度图值小的话&…...
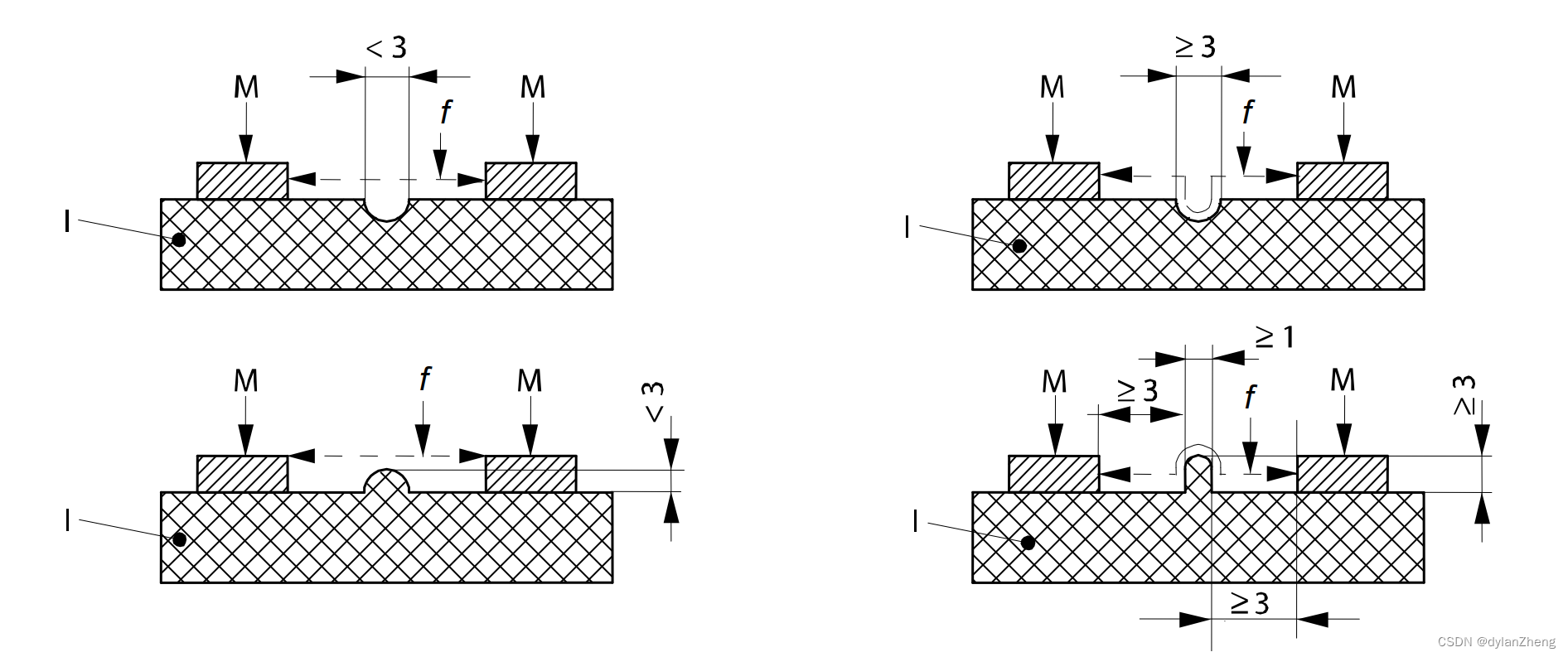
本质安全设备标准(IEC60079-11)的理解(四)
本质安全设备标准(IEC60079-11)的理解(四) 对于标准中“Separation”的理解 IEC60079-11使用了较长的篇幅来说明设计中需要考虑到的各种间距, 这也从一定程度上说明了间距比较重要,在设计中是需要认真考虑…...

(record)QEMU安装最小linux系统——TinyCore(命令行版)
文章目录QEMU安装最小linux系统——TinyCore参考QEMU使用qemu创建tinycore虚拟机再次启动文件保存QEMU安装最小linux系统——TinyCore 简单记录安装过程和记录点 参考 [原创] qemu 与 Tiny Core tinycore的探索 QEMU qemu不多介绍,这里是在WSL2上安装的linux版…...

C++中的cast类型转换
reinterpret_cast用法:reinpreter_cast<type-id> (expression)type-id必须是一个指针、引用、算术类型、函数指针或者成员指针。它可以把一个指针转换成一个整数,也可以把一个整数转换成一个指针。这个操作符能够在非相关的类型之间转换。操作结果…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
