【一文速通】各种机器学习算法的特点及应用场景
近邻 (Nearest Neighbor)
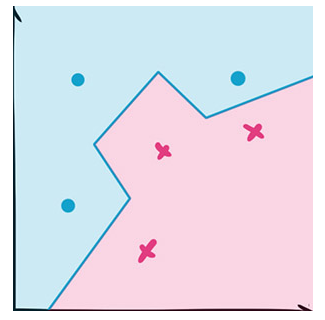
KNN算法的核心思想是,如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时,只与极少量的相邻样本有关。
适用情景:
由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
贝叶斯 (Bayesian)
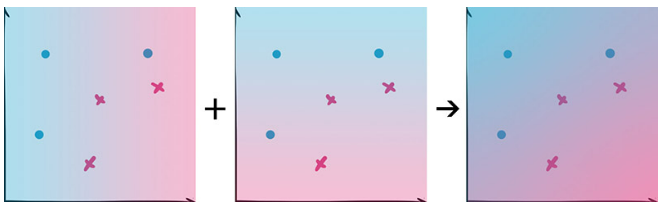
优点:
对待预测样本进行预测,过程简单速度快(想想邮件分类的问题,预测就是分词后进行概率乘积,在log域直接做加法更快)。
对于多分类问题也同样很有效,复杂度也不会有大程度上升。
在分布独立这个假设成立的情况下,贝叶斯分类器效果奇好,会略胜于逻辑回归,同时我们需要的样本量也更少一点。
对于类别类的输入特征变量,效果非常好。对于数值型变量特征,我们是默认它符合正态分布的。
缺点:
对于测试集中的一个类别变量特征,如果在训练集里没见过,直接算的话概率就是0了,预测功能就失效了。当然,我们前面的文章提过我们有一种技术叫做『平滑』操作,可以缓解这个问题,最常见的平滑技术是拉普拉斯估测。
那个…咳咳,朴素贝叶斯算出的概率结果,比较大小还凑合,实际物理含义…恩,别太当真。
朴素贝叶斯有分布独立的假设前提,而现实生活中这些predictor很难是完全独立的。
使用Tips:
大家也知道,很多特征是连续数值型的,但是它们不一定服从正态分布,一定要想办法把它们变换调整成满足正态分布!!
对测试数据中的0频次项,一定要记得平滑,简单一点可以用『拉普拉斯平滑』。
先处理处理特征,把相关特征去掉,因为高相关度的2个特征在模型中相当于发挥了2次作用。
朴素贝叶斯分类器一般可调参数比较少,比如scikit-learn中的朴素贝叶斯只有拉普拉斯平滑因子alpha,类别先验概率class_prior和预算数据类别先验fit_prior。模型端可做的事情不如其他模型多,因此我们还是集中精力进行数据的预处理,以及特征的选择吧。
那个,一般其他的模型(像logistic regression,SVM等)做完之后,我们都可以尝试一下bagging和boosting等融合增强方法。咳咳,很可惜,对朴素贝叶斯里这些方法都没啥用。原因?原因是这些融合方法本质上是减少过拟合,减少variance的。朴素贝叶斯是没有variance可以减小。
朴素贝叶斯训练/建模
理论干货和注意点都说完了,来提提怎么快速用朴素贝叶斯训练模型吧。博主一直提倡要站在巨人的肩膀上编程(其实就是懒…同时一直很担忧写出来的代码的健壮性…),咳咳,我们又很自然地把scikit-learn拿过来了。scikit-learn里面有3种不同类型的朴素贝叶斯:
高斯分布型:用于classification问题,假定属性/特征是服从正态分布的。
多项式型:用于离散值模型里。比如文本分类问题里面我们提到过,我们不光看词语是否在文本中出现,也得看出现的次数。如果总词数为n,出现词数为m的话,说起来有点像掷骰子n次出现m次这个词的场景。
伯努利型:这种情况下,就如之前博文里提到的bag of words处理方式一样,最后得到的特征只有0(没出现)和1(出现过)。
根据你的数据集,可以选择scikit-learn中以上任意一种朴素贝叶斯,我们直接举个简单的例子,用高斯分布型朴素贝叶斯建模
适用情景:
需要一个比较容易解释,而且不同维度之间相关性较小的模型的时候。可以高效处理高维数据,虽然结果可能不尽如人意。
文本分类/垃圾文本过滤/情感判别:这大概会朴素贝叶斯应用做多的地方了,即使在现在这种分类器层出不穷的年代,在文本分类场景中,朴素贝叶斯依旧坚挺地占据着一席之地。原因嘛,大家知道的,因为多分类很简单,同时在文本数据中,分布独立这个假设基本是成立的。而垃圾文本过滤(比如垃圾邮件识别)和情感分析(微博上的褒贬情绪)用朴素贝叶斯也通常能取得很好的效果。
多分类实时预测:这个是不是不能叫做场景?对于文本相关的多分类实时预测,它因为上面提到的优点,被广泛应用,简单又高效。
推荐系统:是的,你没听错,是用在推荐系统里!!朴素贝叶斯和协同过滤(Collaborative Filtering)是一对好搭档,协同过滤是强相关性,但是泛化能力略弱,朴素贝叶斯和协同过滤一起,能增强推荐的覆盖度和效果。
决策树 (Decision tree)
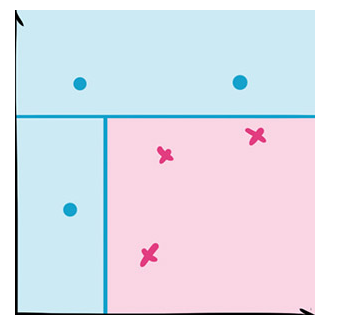
决策树的特点是它总是在沿着特征做切分。随着层层递进,这个划分会越来越细。
优点:
建立决策树模型过程中比较简单,而且算法、决策规则很容易理解。采用决策树模型可以给用户提供可视化和直观化,全面掌握具体情况。决策树的应用范围比较广,无论是分类还是回归,都是可以使用决策树,同时还能根据类别进行不同的分类。决策树即可以处理数值型的样本,还能处理连续的样本。
缺点:
决策树总是会在训练数据时,出现比较复杂的结构,就需要进行大量的过拟合。不过用户可以通过剪枝的方式,来缓解过拟合,例如限制树的高度,或者是规定叶子节点中的最少样本数量等等。
适用情景:
因为它能够生成清晰的基于特征(feature)选择不同预测结果的树状结构,数据分析师希望更好的理解手上的数据的时候往往可以使用决策树。
应用决策树决策方法必须具备以下条件:
(1)具有决策者期望达到的明确目标
(2)存在决策者可以选择的两个以上的可行的备选方案
(3)存在决策者无法控制的两个以上不确定因素
(4)不同方案在不同因素下的收益或损失可以计算出来
(5)决策者可以估计不确定因素发生的概率
受限于它的简单性,决策树更大的用处是作为一些更有用的算法的基石。
随机森林 (Random forest)
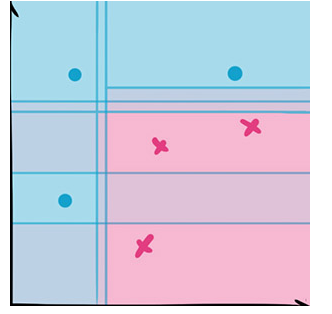
优点:
由于采用了集成算法,本身精度比大多数单个算法要好
在测试集上表现良好,由于两个随机性的引入,使得随机森林不容易陷入过拟合(样本随机,特征随机)
在工业上,由于两个随机性的引入,使得随机森林具有一定的抗噪声能力,对比其他算法具有一定优势
由于树的组合,使得随机森林可以处理非线性数据,本身属于非线性分类(拟合)模型
它能够处理很高维度(feature很多)的数据,并且不用做特征选择,对数据集的适应能力强:既能处理离散型数据,也能处理连续型数据,数据集无需规范化
训练速度快,可以运用在大规模数据集上
可以处理缺省值(单独作为一类),不用额外处理
由于有袋外数据(OOB),可以在模型生成过程中取得真实误差的无偏估计,且不损失训练数据量
在训练过程中,能够检测到feature间的互相影响,且可以得出feature的重要性,具有一定参考意义
由于每棵树可以独立、同时生成,容易做成并行化方法
由于实现简单、精度高、抗过拟合能力强,当面对非线性数据时,适于作为基准模型
缺点:
当数据维度过多时,由于会对每个特征的每个值进行不纯度计算,所以效率会比单纯决策树要慢;
无法给出连续的输出,生成的结果不会超出给定的训练集中结果的范围。
适用情景:
数据维度相对低(几十维),同时对准确性有较高要求时。因为不需要很多参数调整就可以达到不错的效果,基本上不知道用什么方法的时候都可以先试一下随机森林。
既可以用于分类也可以用于回归问题,不适用于需要高实时的场景。
SVM (Support vector machine)
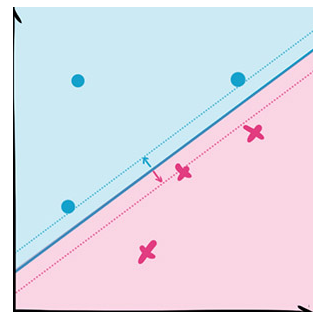
SVM的核心思想就是找到不同类别之间的分界面,使得两类样本尽量落在面的两边,而且离分界面尽量远。
最早的SVM是平面的,局限很大。但是利用核函数(kernel function),我们可以把平面投射(mapping)成曲面,进而大大提高SVM的适用范围。
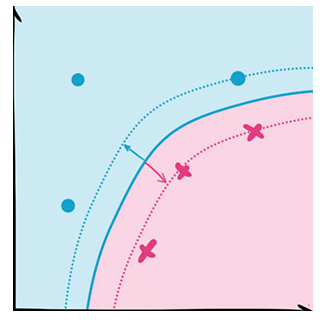
适用情景:
SVM(支持向量机)主要用于分类问题,主要的应用场景有字符识别、面部识别、行人检测、文本分类等领域,在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别、分类(异常值检测)以及回归分析。
逻辑回归 (Logistic regression)
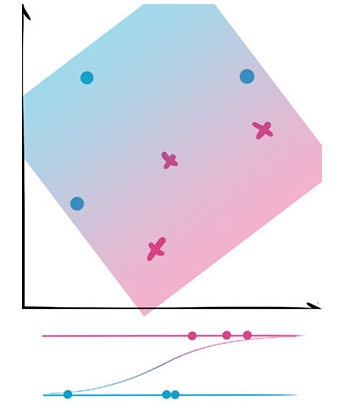
优点:
(模型)模型清晰,背后的概率推导经得住推敲。
(输出)输出值自然地落在0到1之间,并且有概率意义(逻辑回归的输出是概率么?https://www.jianshu.com/p/a8d6b40da0cf)。
(参数)参数代表每个特征对输出的影响,可解释性强。
(简单高效)实施简单,非常高效(计算量小、存储占用低),可以在大数据场景中使用。
(可扩展)可以使用online learning的方式更新轻松更新参数,不需要重新训练整个模型。
(过拟合)解决过拟合的方法很多,如L1、L2正则化。
(多重共线性)L2正则化就可以解决多重共线性问题。
缺点:
(特征相关情况)因为它本质上是一个线性的分类器,所以处理不好特征之间相关的情况。
(特征空间)特征空间很大时,性能不好。
(精度)容易欠拟合,精度不高。
适用情景:
LR同样是很多分类算法的基础组件,它的好处是输出值自然地落在0到1之间,并且有概率意义。
因为它本质上是一个线性的分类器,所以处理不好特征之间相关的情况。 虽然效果一般,却胜在模型清晰,背后的概率学经得住推敲。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。
用于分类:适合做很多分类算法的基础组件。
用于预测:预测事件发生的概率(输出)。
用于分析:单一因素对某一个事件发生的影响因素分析(特征参数值)。
基本假设:输出类别服从伯努利二项分布。
样本线性可分。
特征空间不是很大的情况。
不必在意特征间相关性的情景。
后续会有大量新数据的情况。
判别分析 (Discriminant analysis)
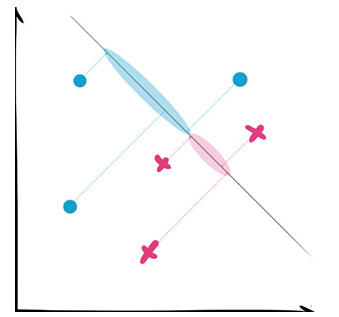
判别分析主要是统计那边在用,所以我也不是很熟悉,临时找统计系的闺蜜补了补课。这里就现学现卖了。
判别分析的典型例子是线性判别分析(Linear discriminant analysis),简称LDA。(这里注意不要和隐含狄利克雷分布(Latent Dirichlet allocation)弄混,虽然都叫LDA但说的不是一件事。)LDA的核心思想是把高维的样本投射(project)到低维上,如果要分成两类,就投射到一维。要分三类就投射到二维平面上。这样的投射当然有很多种不同的方式,LDA投射的标准就是让同类的样本尽量靠近,而不同类的尽量分开。对于未来要预测的样本,用同样的方式投射之后就可以轻易地分辨类别了。
使用情景:
判别分析适用于高维数据需要降维的情况,自带降维功能使得我们能方便地观察样本分布。它的正确性有数学公式可以证明,所以同样是很经得住推敲的方式。
但是它的分类准确率往往不是很高,所以不是统计系的人就把它作为降维工具用吧。
同时注意它是假定样本成正态分布的,所以那种同心圆形的数据就不要尝试了。
神经网络 (Neural network)
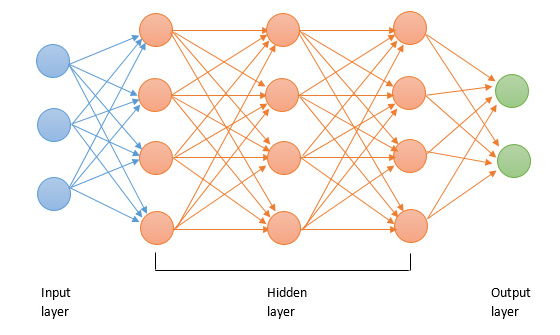
优点:
分类的准确度高;
并行分布处理能力强,分布存储及学习能力强,
对噪声神经有较强的鲁棒性和容错能力,能充分逼近复杂的非线性关系;
具备联想记忆的功能。
缺点:
神经网络需要大量的参数,如网络拓扑结构、权值和阈值的初始值;
不能观察之间的学习过程,输出结果难以解释,会影响到结果的可信度和可接受程度;
学习时间过长,甚至可能达不到学习的目的。
使用情景:
数据量庞大,参数之间存在内在联系的时候。
当然现在神经网络不只是一个分类器,它还可以用来生成数据,用来做降维
提升算法(Boosting)
接下来讲的一系列模型,都属于集成学习算法(Ensemble Learning),基于一个核心理念:三个臭皮匠,顶个诸葛亮。
翻译过来就是:当我们把多个较弱的分类器结合起来的时候,它的结果会比一个强的分类器更典型的例子是AdaBoost。
AdaBoost的实现是一个渐进的过程,从一个最基础的分类器开始,每次寻找一个最能解决当前错误样本的分类器。用加权取和(weighted sum)的方式把这个新分类器结合进已有的分类器中。
它的好处是自带了特征选择(feature selection),只使用在训练集中发现有效的特征(feature)。这样就降低了分类时需要计算的特征数量,也在一定程度上解决了高维数据难以理解的问题。
最经典的AdaBoost实现中,它的每一个弱分类器其实就是一个决策树。这就是之前为什么说决策树是各种算法的基石。
使用情景:
好的Boosting算法,它的准确性不逊于随机森林。虽然在[1]的实验中只有一个挤进前十,但是实际使用中它还是很强的。因为自带特征选择(feature selection)所以对新手很友好,是一个“不知道用什么就试一下它吧”的算法。
装袋算法(Bagging)
同样是弱分类器组合的思路,相对于Boosting,其实Bagging更好理解。它首先随机地抽取训练集(training set),以之为基础训练多个弱分类器。然后通过取平均,或者投票(voting)的方式决定最终的分类结果。
因为它随机选取训练集的特点,Bagging可以一定程度上避免过渡拟合(overfit)。
在[1]中,最强的Bagging算法是基于SVM的。如果用定义不那么严格的话,随机森林也算是Bagging的一种。
使用情景:
相较于经典的必使算法,Bagging使用的人更少一些。一部分的原因是Bagging的效果和参数的选择关系比较大,用默认参数往往没有很好的效果。
虽然调对参数结果会比决策树和LR好,但是模型也变得复杂了,没事有特别的原因就别用它了。
对于稳定的模型来说,Bagging并不会工作地很好,而Boosting可得会有帮助。如果在训练集上有noisy数据,Boosting会很快地过拟合,降低模型的性能,而Bagging不存在这样地问题。
一句话总结:在实际应用中,Bagging通常都会有帮助,而Boosting是一把利剑,用好的情况下肯定会比Bagging出色,但是用不好很可能会伤到自己。
隐马尔科夫 (Hidden Markov model,HMM)
这是一个基于序列的预测方法,核心思想就是通过上一个(或几个)状态预测下一个状态。
之所以叫“隐”马尔科夫是因为它的设定是状态本身我们是看不到的,我们只能根据状态生成的结果序列来学习可能的状态。
适用场景:
可以用于序列的预测,可以用来生成序列。条件随机场 (Conditional random field)典型的例子是linear-chain CRF。
HMM在语音中的应用
(1)根据一些特征对部分语意块进行词语切分,然后计算各个词语或语义块的输出概率。
(2)在给定的HMM模型下,用韦特比算法进行计算,求出状态序列,即语义块相关联的域,然后按关联结果抽取各语义项。
相对于语音的概率密度分布表示法,隐马尔科夫模型更能反映出语音的动态时序变化特性,特别是在建模过程中,可以有效结合语音的山下文相关性约束。
HMM在人脸识别中的应用
HMM是用概率统计的方法来进行时序数据识别模拟的分类器。最早将HMM应用于人脸识别的文献根据人脸由上至下各个区域具有自然不变的顺序这一相似共性,即可用一个1D-HMM表示人脸。根据人脸水平方向也就有相对稳定的空间结构,因此可将沿垂直方向划分的状态分别扩充为一个1D-HMM,共同组成了2D-HMM。
HMM在人脸表情识别中的应用
人脸表情识别的任务就在于通过表情图像来分析和建立HMM,对表情进行训练和识别
整理不易,且用且珍惜,希望大家点赞+收藏+评论,您的支持是我持续更新的动力~
相关文章:

【一文速通】各种机器学习算法的特点及应用场景
近邻 (Nearest Neighbor)KNN算法的核心思想是,如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定…...

多传感器融合定位十四-基于图优化的定位方法
多传感器融合定位十四-基于图优化的定位方法1. 基于图优化的定位简介1.1 核心思路1.2 定位流程2. 边缘化原理及应用2.1 边缘化原理2.2 从滤波角度理解边缘化3. 基于kitti的实现原理3.1 基于地图定位的滑动窗口模型3.2 边缘化过程4. lio-mapping 介绍4.1 核心思想4.2 具体流程4.…...

PHP基于TCPDF第三方类生成PDF文件
最近在研发招聘的系统 遇到了这个问题 转换pdf 折腾了很久 分享一下PHP基于TCPDF第三方类生成PDF文件最近遇到一个需求,需要根据数据库的字段生成表格式的PDF文件并发送邮箱第一步、我们先去官网上面去下载tcpdf的类:http://www.tcpdf.org/或者是从githu…...
:Sentinel定义资源的方式)
SpringCloud(19):Sentinel定义资源的方式
Sentinel除了基本的定义资源的方式之外,还有其他的定义资源的方式,具体如下: 抛出异常的方式定义资源返回布尔值方式定义资源异步调用支持注解方式定义资源主流框架的默认适配1 抛出异常的方式定义资源 Sentinel中的SphU包含了try-catch风格的API。用这种方式,当资源发生了…...

前端 ES6 之 Promise 实践应用与控制反转
Promise 主要是为解决程序异步处理而生的,在现在的前端应用中无处不在,已然成为前端开发中最重要的技能点之一。它不仅解决了以前回调函数地狱嵌套的痛点,更重要的是它提供了更完整、更强大的异步解决方案。 同时 Promise 也是前端面试中必不…...

LightGBM
目录 1.LightGBM的直方图算法(Histogram) 直方图做差加速 2.LightGBM得两大先进技术(GOSS&EFB) 2.1 单边梯度抽样算法(GOSS) 2.2 互斥特征捆绑算法(EFB) 3.LightGBM得生长策略(leaf-wise) 通过与xgboost对比,在这里列出lgb新提出的几个方面的技术 1.Ligh…...
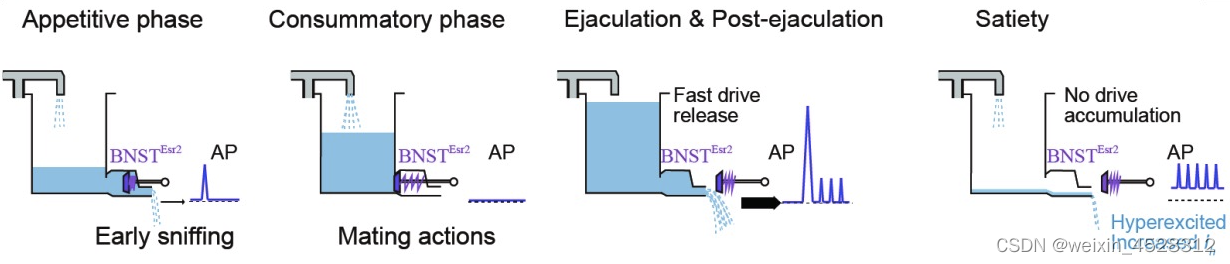
Science:北京脑研究中心李莹实验室揭示性满足感的分子机制
短暂的社交经历(例如,性经历)可导致内部状态的长期变化并影响社会行为,如交配、攻击。例如,在成功交配射精后,许多物种迅速表现出对交配倾向的抑制有数小时、数天或更长时间,这种效应称为性满足…...

Element UI框架学习篇(三)
Element UI框架学习篇(三) 实现简单登录功能(不含记住密码) 1 准备工作 1.1 在zlz包下创建dto包,并创建userDTO类(传输对象) package com.zlz.dto;import lombok.Data;/* DTO 数据传输对象 用户表的传输对象 调用控制器传参使用 VO 控制器返回的视图对象 与页面对应 PO 数据…...
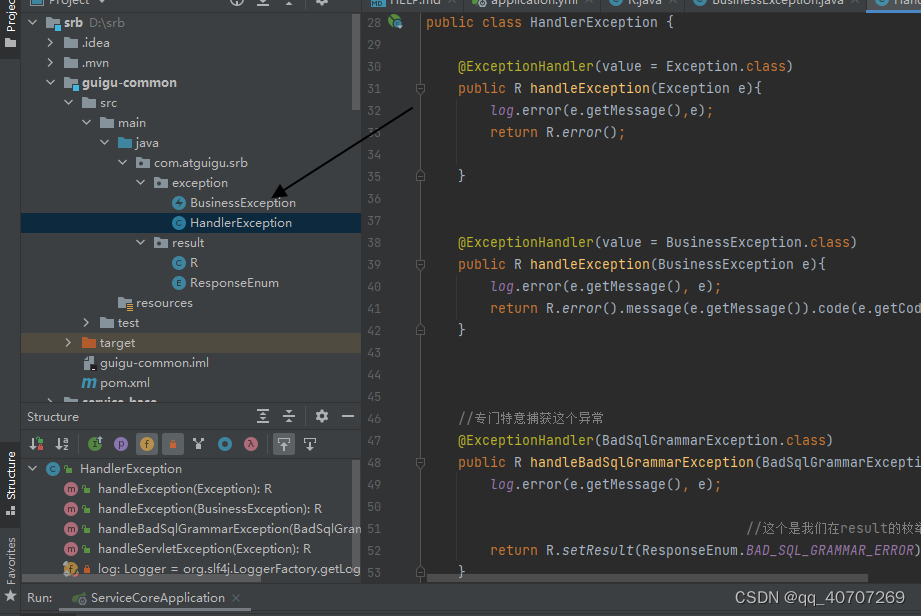
尚硅谷的尚融宝项目
先建立一个Maven springboot项目 进来先把src删掉,因为是一个父项目,我们删掉src之后,pom里配置的东西,也能给别的模块使用。 改一下springboot的版本号码 加入依赖和依赖管理: <properties><java.versi…...

12 Day:内存管理
前言:今天我们要完成我们操作系统的内存管理,以及一些数据结构和小组件的实现,在此之前大家需要了解我们前几天一些重要文件的内存地址存放在哪,以便我们更好的去编写内存管理模块 一,实现ASSERT断言 不知道大家有没有…...

linux基本功系列之lsof命令实战
文章目录前言一. lsof命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示系统打开的文件3.2 查找某个文件相关的进程3.3 列出某个用户打开的文件信息3.4 列出某个程序进程所打开的文件信息3.5 查看某个进程号打开的文件3.6 列出所有的网络连接3.7 列出谁在使用某个端口3.8 恢…...
基础篇:02-SpringCloud概述
1.SpringCloud诞生 基于前面章节,我们深知微服务已成为当前开发的主流技术栈,但是如dubbo、zookeeper、nacos、rocketmq、rabbitmq、springboot、redis、es这般众多技术都只解决了一个或一类问题,微服务并没有一个统一的解决方案。开发人员或…...
【软件测试】软件测试工作上95%会遇到的问题,你遇到多少?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、测试负责人要进行…...

4.5.4 LinkedList
文章目录1.特点2.常用方法3.练习:LinkedList测试1.特点 链表,两端效率高,底层就是链表实现的 List接口的实现类,底层的数据结构为链表,内存空间是不连续的 元素有下标,有序允许存放重复的元素在数据量较大的情况下,查询慢&am…...

Python之FileNotFoundError: [Errno 2] No such file or directory问题处理
错误信息:FileNotFoundError: [Errno 2] No such file or directory: ../AutoFrame/temp/report.xlsx相对于当前文件夹的路径,其实就是你写的py文件所在的文件夹路径!python在对文件的操作时,需要特别注意文件地址的书写。文件的路…...

C语言中耳熟能详的printf与scanf
没有什么比时间更有说服力了,因为时间无需通知我们就可以改变一切了。---余华《活着》大家好,今天给大家分享的是C语言中的scanf与printf函数,一提起这两个函数,大家可能觉得这不就是打印和输入嘛?有什么可以说的&…...
【数据结构】复杂度讲解
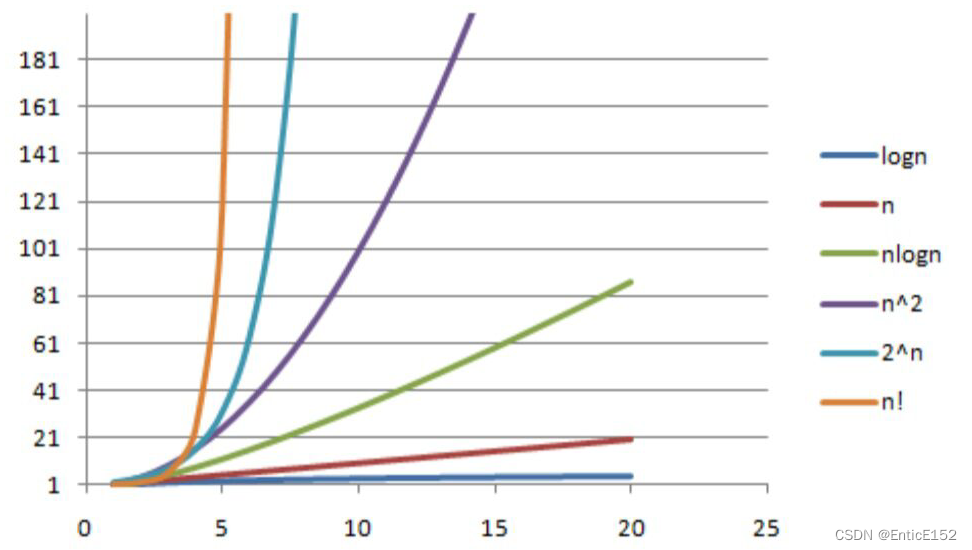
目录 时间复杂度与空间复杂度:: 1.算法效率 2.时间复杂度 3.空间复杂度 4.常见时间复杂度以及复杂度OJ练习 时间复杂度与空间复杂度:: 什么是数据结构? 数据结构中是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关…...

JAVA-线程池技术
目录 概念 什么是线程? 什么是线程池? 线程池出现背景 线程池原理图 JAVA提供线程池 线程池参数 如果本篇博客对您有一定的帮助,大家记得留言点赞收藏哦。 概念 什么是线程? 是操作系统能够进行运算调度的最小单位。&am…...
)
【C++】从0到1入门C++编程学习笔记 - 提高编程篇:STL常用算法(算术生成算法)
文章目录一、accumulate二、fill学习目标: 掌握常用的算术生成算法 注意: 算术生成算法属于小型算法,使用时包含的头文件为 #include <numeric> 算法简介: accumulate // 计算容器元素累计总和 fill // 向容器中添加元…...

【C++】static成员
💙作者:阿润菜菜 📖专栏:C 目录 概念 特性 出个题 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量; 用static修饰的成员函数,称之为静态…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
