【力扣每日一题】2023.9.10 课程表Ⅱ
目录
题目:
示例:
分析:
代码:
题目:
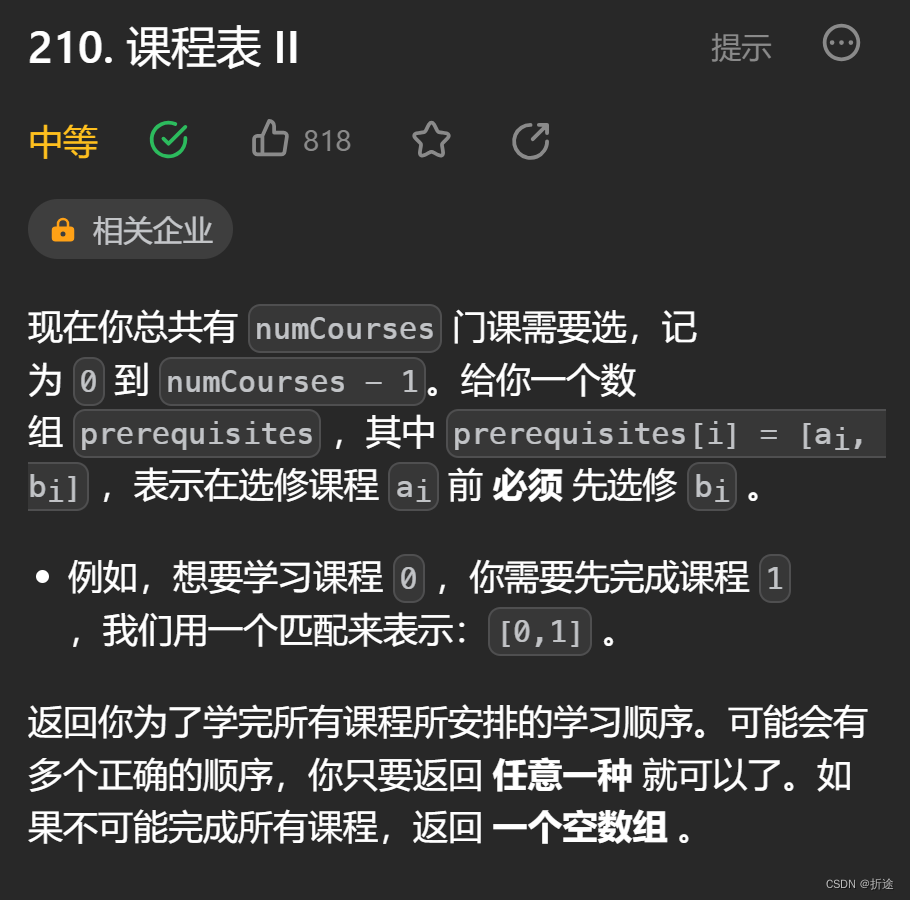
示例:

分析:
今天的题目和昨天类似,不过今天要我们求出学习所有课程的先后顺序。
昨天只需要我们求出能否学习完所有课程,因此我们只需要判断构建出的有向图中是否有环即可,而今天的题我们就不能简单判断有没有环了。
要返回学习课程的先后顺序,最简单最直接的方法就是模拟。
我们跟昨天一样,首先先把有向图构建出,接着我们再模拟学习,模拟之前我们还需要拿一个数组来存放学习课程的顺序,以及一个set来记录学过的课程,其实数组和set里的元素是一致的,不过set更方便统计set中是否含有某个元素。
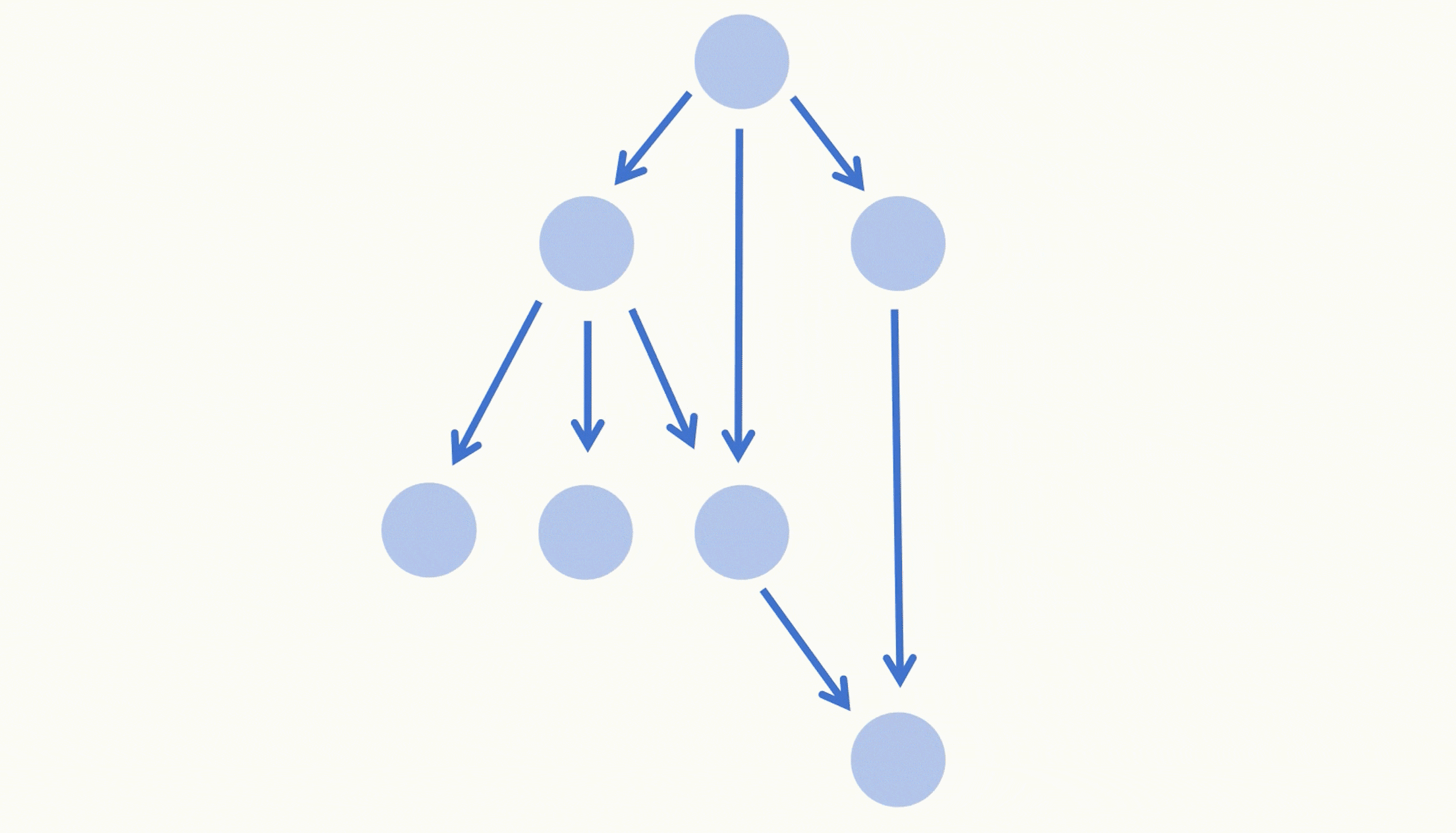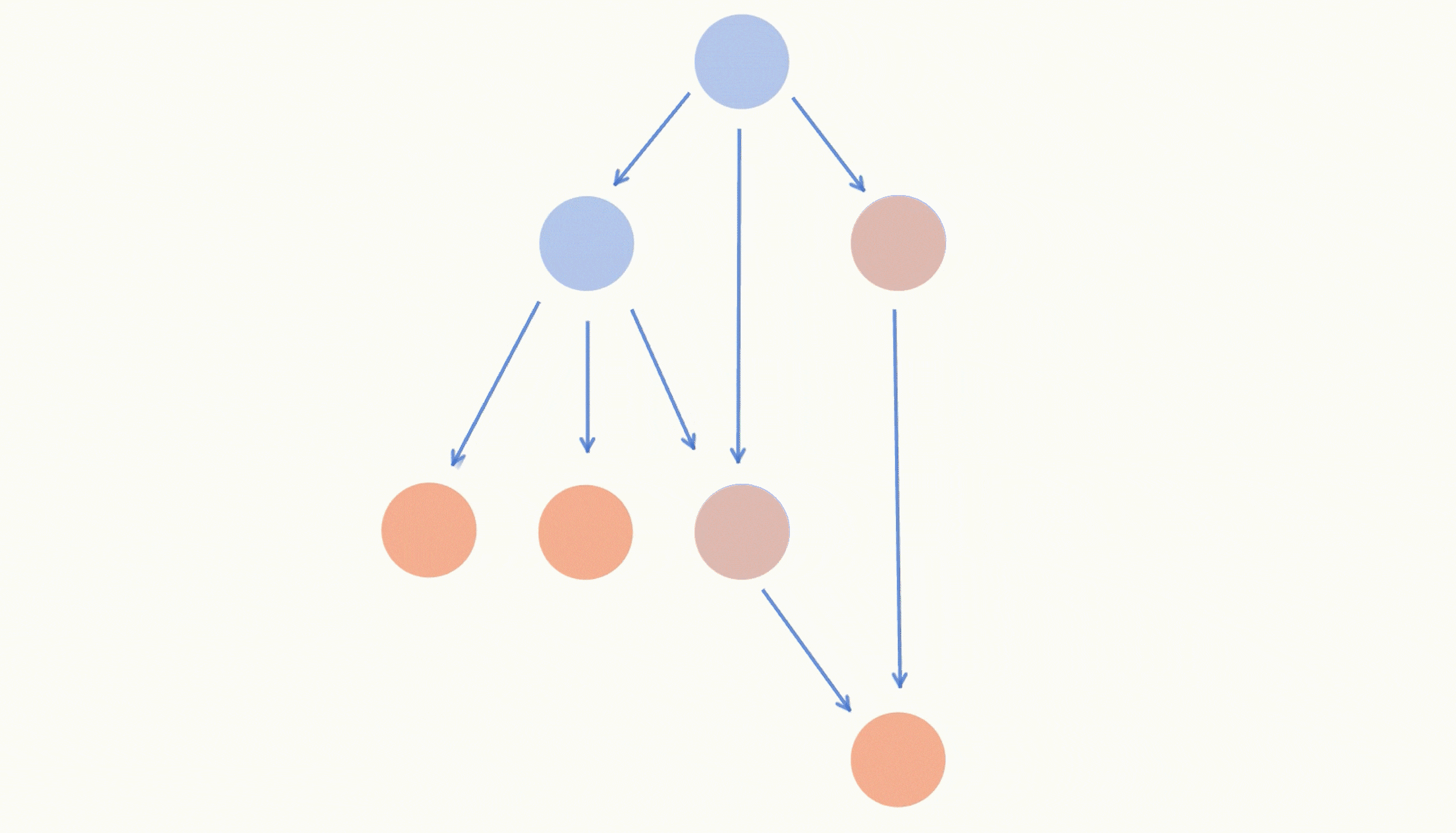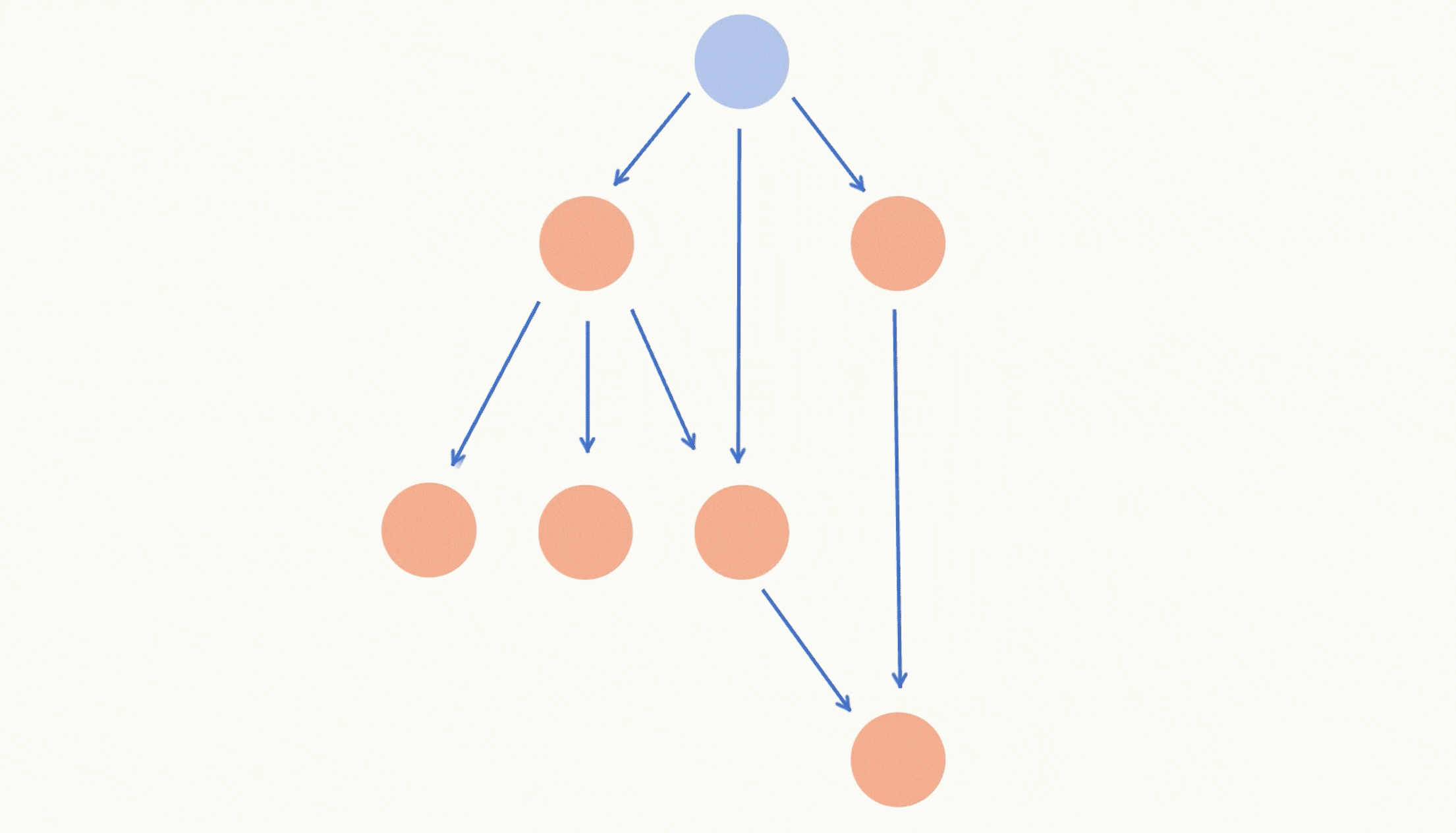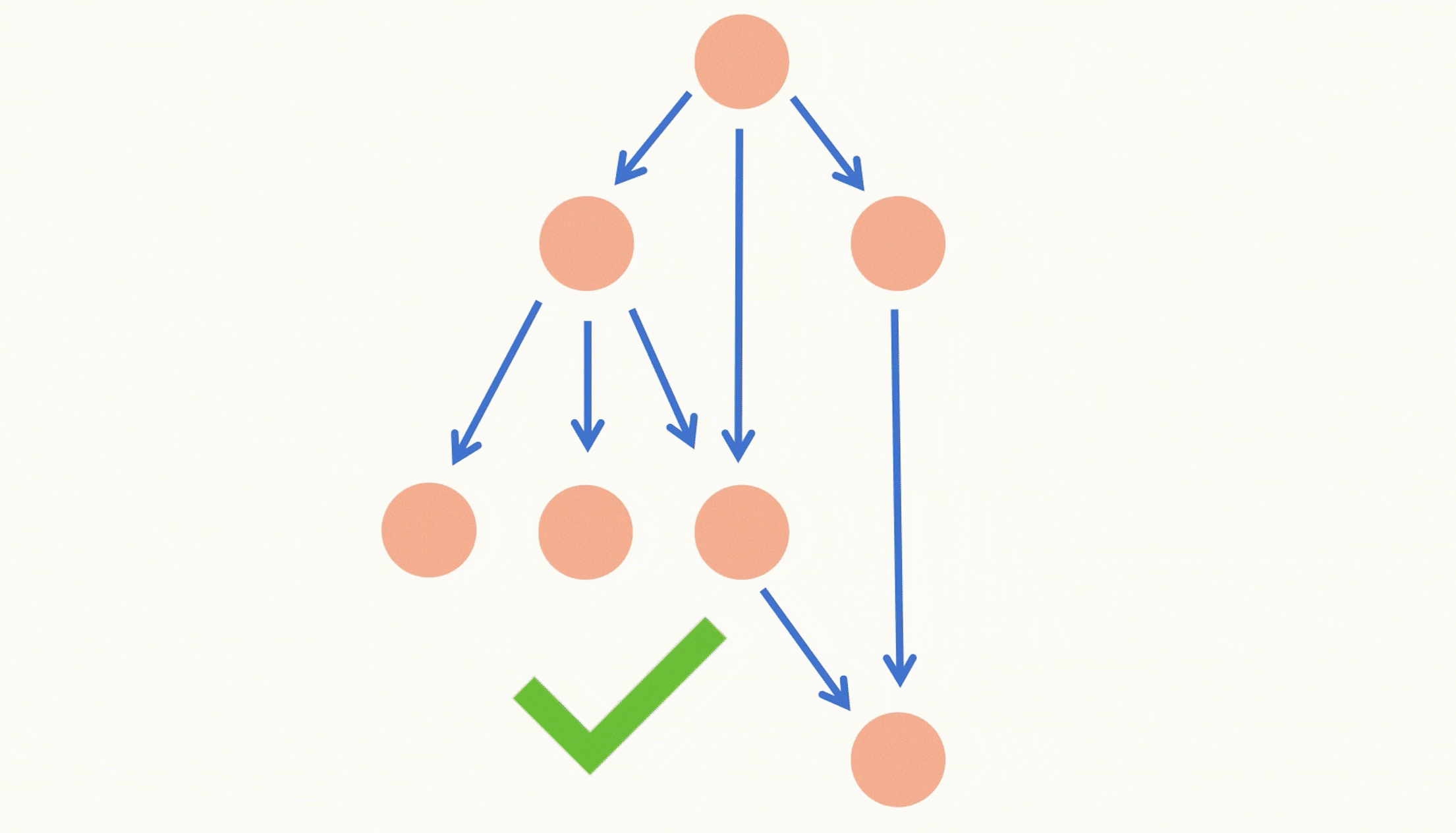
每次学习我们都把所有课程遍历一遍,如果课程我们没有学过(不在set里),我们就遍历这门课程的先修课程,如果它的先修课程全部都在set中,那么我们本轮学习就可以学这门课程,把它添加进答案数组以及set中。
课程遍历完毕之后,我们还需要做一个判断,如果本轮学习没有学习到任何课程,那么就表示我们无法学习到所有的课程(图中有环),返回空数组即可。
一直重复上述模拟学习的过程,直到答案数组的长度等于课程数目了,就表示我们学习完了所有的课程,这时退出循环,返回答案数组即可。
代码:
class Solution {
public:unordered_map<int,vector<int>>m;vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {for(auto& p:prerequisites){ //构建有向图 if(m.find(p[0])==m.end()) m[p[0]]=vector<int>(0);m[p[0]].push_back(p[1]);}vector<int>res; unordered_set<int>s; //用于统计已经学习的课程int last=0; //记录上一轮的学习课程数while(res.size()!=numCourses){for(int i=0;i<numCourses;i++){ //遍历所有课程 if(s.count(i)==0){ //如果没学过课程那么进入判断bool flag=true;for(int c:m[i]){ if(s.count(c)==0){flag=false;break;}}if(flag){ //如果本课程的所有先修课都学过,那么添加进答案res.push_back(i);s.insert(i);}}}//如果本轮学习过后,学习课程和上一轮一样,那么我们无法学完所有课程,返回空if(last==res.size()) return vector<int>(0);last=res.size();}return res;}
};相关文章:

【力扣每日一题】2023.9.10 课程表Ⅱ
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 今天的题目和昨天类似,不过今天要我们求出学习所有课程的先后顺序。 昨天只需要我们求出能否学习完所有课程,因此…...

VSCODE CMAKE C++ 工程调试, C++不以科学计数法输出并控制小数位数
1. VSCODE调试CMAKE工程配置1.1 修改CMakeLists.txt文件1.2. 程序中1.3. launch.json配置1.4 开始调试1.5 注意 2. C设置输出浮点数且保留位数固定 1. VSCODE调试CMAKE工程配置 1.1 修改CMakeLists.txt文件 加这一句 set(CMAKE_BUILD_TYPE "Debug")1.2. 程序中 在…...

Drools规则引擎入门学习记录
业务开发过程中,对于某些判断性的通用规则是基于if-else封装,还是基于策略模式封装?无论以上那种封装出来的方法,只能在单体软件包中共用,且不能无感部署,然而对于业务而言,可能规则改变的比较频…...
肖sir__设计测试用例方法之判定表06_(黑盒测试)
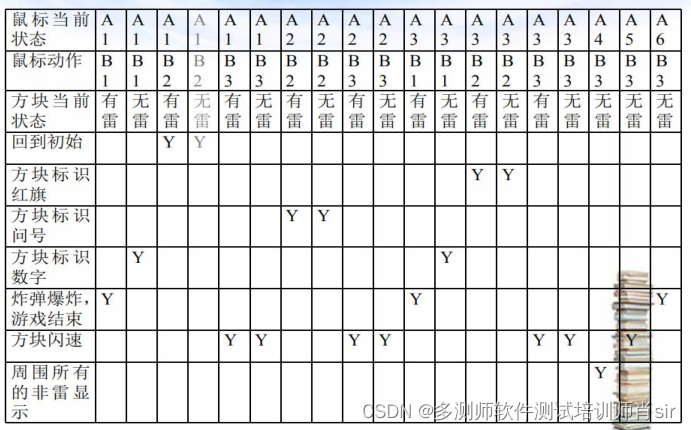
设计测试用例方法之判定表 1、判定表:是一种表达逻辑判断的工具。 2、判定表:包含四部分 1)条件桩(condition stub):列出问题的 所有条件(通常条件次序无关紧要)。 2)条件项&#x…...

<图像处理> 空间滤波基础
空间滤波基础 图像滤波是一种常见的图像处理技术,用于平滑图像、去除噪音和边缘检测等任务。图像滤波的基本原理是在进行卷积操作时,通过把每个像素的值替换为该像素及其邻域的设定的函数值来修改图像。 预备知识:可分离滤波核、边缘填充。…...

如何在Django中使用django-crontab启动定时任务、关闭任务以及关闭指定任务
安装django-crontab包: pip install django-crontab 在Django项目的settings.py文件中,找到INSTALLED_APPS配置,并添加django_crontab到列表中: INSTALLED_APPS [ ... django_crontab,... ] 在settings.py文件的末尾,添加以下配置以设…...

mysql配置项整理
二、:mysql服务器参数 general 基础配置 datadir/var/lib/mysql #数据文件存放的目录 socket/var/lib/mysql/mysql.sock #mysql.socket表示server和client在同一台服务器,并且使用localhost进行连接,就会使用socket进行连接 pid_file/v…...

【KRouter】一个简单且轻量级的Kotlin Routing框架
【KRouter】一个简单且轻量级的Kotlin Routing框架 KRouter(Kotlin-Router)是一个简单而轻量级的Kotlin路由框架。 具体来说,KRouter是一个通过URI来发现接口实现类的框架。它的使用方式如下: val homeScreen KRouter.route&l…...

时间管理类书籍阅读笔记
背景 这段时间看了时间管理方面的书籍,大部分和早晨时间利用相关。之所以有了利用早晨时间的想法,是某天下班后,感觉很疲惫,什么都不想做,于是就打了一晚上游戏,然后第二天重复着这样的生活。 突然意识到…...
CSS文字居中对齐学习
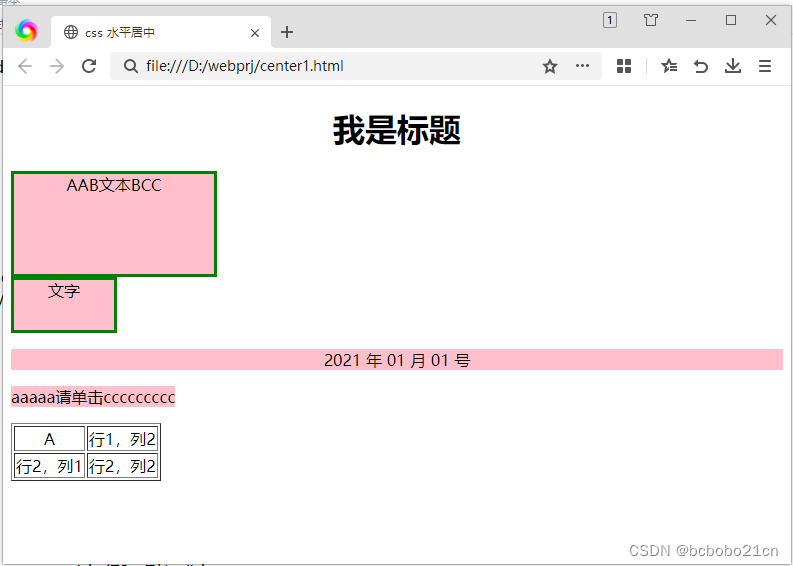
CSS使用text-align属性设置文字对齐方式;text-align:center,这样就设置了文字居中对齐; <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>css 水平居中</title><style>.box …...

《论文阅读》CARE:通过条件图生成的共情回复因果关系推理 EMNLP 2022
《论文阅读》CARE:通过条件图生成的移情反应因果关系推理 前言简介基础知识TransformerVariational Graph Auto-Encoder 变分图自编码器`邻接矩阵(adjacency matrix)``图神经网络(GNN)``图卷积神经网络(GCN)``自编码器(Auto Encoder)``图自编码器(GAE)``变分图自编码…...
React 开发一个移动端项目(1)
技术栈: 项目搭建:React 官方脚手架 create-react-appreact hooks状态管理:redux 、 redux-thunkUI 组件库:antd-mobileajax请求库:axios路由:react-router-dom 以及 historyCSS 预编译器:sass…...
c#查看代码的执行耗时( Stopwatch )
我们如果需要看某段代码的执行耗时,会通过如下的方式进行查看 using System.Diagnostics; private void button1_Click(object sender, EventArgs e){Stopwatch sw Stopwatch.StartNew();//sw.Start();StringBuilder sb new StringBuilder();for(int i 0; i <…...

Python网络爬虫库:轻松提取网页数据的利器
网络爬虫是一种自动化程序,它可以通过访问网页并提取所需的数据。Python是一种流行的编程语言,拥有许多强大的网络爬虫库。在本文中,我们将介绍几个常用的Python网络爬虫库以及它们的使用。 Requests库 Requests是一个简单而优雅的HTTP库&…...

YOLOv5算法改进(15)— 更换Neck之AFPN
前言:Hello大家好,我是小哥谈。在YOLOv5中添加AFPN(Adaptive Feature Pyramid Network)可以提高目标检测的准确性。AFPN是一种用于目标检测任务的功能增强模块,它能够自适应地融合来自不同层级的特征图,以提…...
Vue2项目练手——通用后台管理项目第七节
Vue2项目练手——通用后台管理项目 用户管理分页使用的组件Users.vuemock.js 关键字搜索区Users.vue 权限管理登录页面样式修改Login.vue 登录权限使用token对用户鉴,使用cookie对当前信息保存(类似localstorage)Login.vuerouter/index.js 登…...
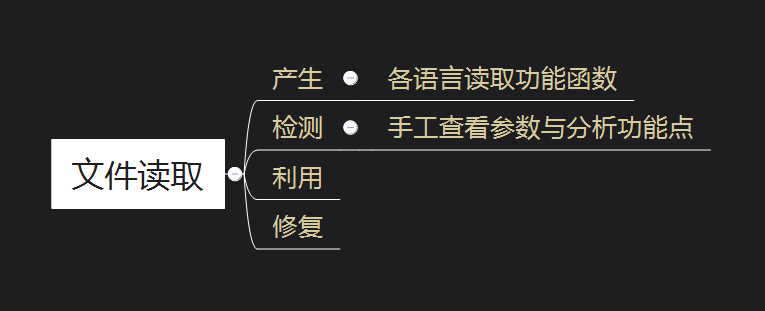
《Web安全基础》04. 文件操作安全
web 1:文件操作安全2:文件上传漏洞2.1:简介2.2:防护与绕过2.3:WAF 绕过2.3.1:数据溢出2.3.2:符号变异2.3.3:数据截断2.3.4:重复数据 3:文件包含漏洞4…...
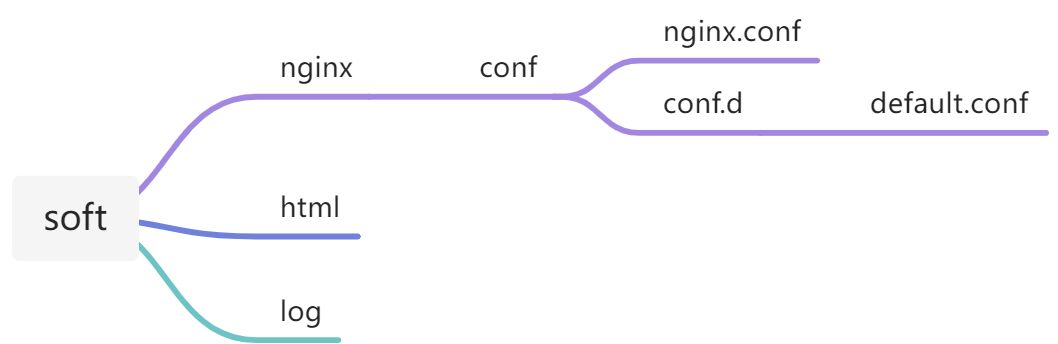
docker-compose安装nginx
基于docker-compose安装nginx 目录 一、目录结构 1、docker-compose.yml 2、nginx.conf 3、default.conf 4、index.html 二、访问测试 一、目录结构 1、docker-compose.yml version: 3 services:nginx:image: registry.cn-hangzhou.aliyuncs.com/zhengqing/nginx:1.21.1…...

报错处理:MySQL无法启动
报错环境: Linux MySQL 具体报错: Cant connect to local MySQL server through socket /var/run/mysqld/mysqld.sock 排错思路: 当尝试启动MySQL服务时,如果出现无法连接到MySQL服务的错误,可能是由于MySQL服务未正确…...

Vue中表单手机号验证与手机号归属地查询
下面是一篇关于Vue中如何进行表单手机号验证与手机号归属地查询的Markdown格式的文章,包含代码示例。 Vue中表单手机号验证与手机号归属地查询 手机号验证和归属地查询是许多Web应用程序中常见的功能之一。在Vue.js中,我们可以轻松地实现这两个功能。本…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
