嵌入式-数据进制之间的转换

目录
一.简介
1.1十进制
1.2二进制
1.3八进制
1.4十六进制
二.进制转换
2.1二进制-十进制转换
2.2八进制-十进制转换
2.3十六进制-十进制转换
2.4十进制-二进制转换
2.5十进制-八进制转换
2.6十进制-十六进制转换
2.7小数部分转换
一.简介
被传入到计算机的数据要转换成0,1的二进制数据才能被计算机识别。为了方便存储,我们将数据以进制的形式存储。
进制也就是进位计数制,是人们规定的一种带进位的计数方法。
对于任何一种进制---X进制,就表示每一位置上的数运算时都是逢X进一位。例如十进制是逢十进一,二进制是逢二进一,十六进制是逢十六进一。
常见的数据进制包括以下几种:
- 十进制。十进制数是指0、1、2、3、4、5、6、7、8、9共十个数字,每逢十进一。
- 二进制。二进制数是指0和1两个数码,每逢二进一。
- 八进制。八进制数是指0、1、2、3、4、5、6、7共八个数字,每逢八进一。
- 十六进制。十六进制数是指0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共十六个数字,每逢十六进一。
1.1十进制
十进制(Decimal System)是一种计数方法,即满十进一,计数单位是101。
十进制计数法是日常使用最多的计数方法,每相邻的两个计数单位之间的进率都为十,即10、100、1000、10000、100000、……,其计数单位为1、10、10^2、10^3、10^4、……,这些计数单位之间的进率都是10,即10^1=10、10^2=10×10=10^3、……、10^n=10×……×10=10^(n+1),以此类推。
十进制计数法最早是由亚里士多德发现的,起因可能是因为人类有十根手指,所以每相邻的两个计数单位之间的进率都是十,这跟人类算数采用十进制可能有一定关系
1.2二进制
二进制是由德国数理哲学大师莱布尼茨在1679年发明的,他在看了中国的《周易》之后受到启发发明了二进制,这也是今天电子计算机技术的基础。
二进制的基数为2,每个数码只能是0和1。在二进制中,数码的进位规则是“逢二进一”,即每位二进制数的权值是2的整数次幂。
二进制在数学和数字电路中应用非常广泛,现代的计算机和依赖计算机的设备里都使用二进制。
二进制的计算案例:
0011(二进制)+ 0101(二进制)= 1000(二进制)
计算过程:
0+0=0
1+1=0(进位)
1+0=1
所以,0011+0101=1000
1.3八进制
八进制是一种以8为基数的计数法,采用0、1、2、3、4、5、6、7八个数字,逢八进1。
八进制在计算机领域被广泛运用,因为与二进制转换简便,同时又避免了二进制的基数大带来的许多麻烦。
八进制数的表示方法通常以0开始,例如:0O、01、02、03、04、05、06、07等。
1.4十六进制
十六进制是用16作为基数的计数系统 。它使用数字0-9和字母A-F(或其大写A-F)表示0到15。例如,十六进制的A表示十进制的10,B表示十进制的11,C表示十进制的12,以此类推。十六进制数通常以0x或0X开头,例如,0x1表示十六进制的1,0x1A表示十六进制的26(1×16+10×1)
二.进制转换
2.1二进制-十进制转换
二进制向十进制转换的方法是按照二进制数的每一位乘以对应的权值(2的幂次方),然后相加得到十进制数。例如,二进制数1101转换为十进制数的计算过程为:
1×2^3+1×2^2+0×2^1+1×2^0=8+4+0+1=13
因此,二进制数1101转换为十进制数为13。
2.2八进制-十进制转换
八进制转换为十进制的方法是按照八进制数的每一位乘以对应的权值(8的幂次方),然后相加得到十进制数。例如,八进制数7654转换为十进制数的计算过程为:
7×8^3+6×8^2+5×8^1+4×8^0=4000+384+40+4=4428
因此,八进制数7654转换为十进制数为4428。
2.3十六进制-十进制转换
十六进制转换为十进制的方法是按照十六进制数的每一位乘以对应的权值(16的幂次方),然后相加得到十进制数。例如,十六进制数3E转换为十进制数的计算过程为:
3×16^1+14×16^0=48+14=62
因此,十六进制数3E转换为十进制数为62。
2.4十进制-二进制转换
十进制转换为二进制的方法是将每一个十进制数除以2,然后将余数按从低位到高位的顺序排列,得到的数就是对应的二进制数。例如,将十进制数23转换为二进制数的过程如下:
23 ÷ 2=11 余 1
11 ÷ 2=5 余 1
5 ÷ 2=2 余 1
2 ÷ 2=1 余 0
1 ÷ 2=0 余 1
从下往上读取余数,得到23的二进制表示为10111。因此,十进制数23转换为二进制数为10111。
2.5十进制-八进制转换
将一个十进制数转换为八进制同样使用除法法则,以下是一种转换方法:
1. 选取需要转换的十进制数。
2. 用该数除以8,得到商和余数。
3. 将余数作为结果的最后一位。
4. 将商作为新的十进制数,重复步骤2和3,直到商为0。
5. 将余数按照从最后一位到第一位的顺序排列,得到转换后的八进制数。
举例说明:
将十进制数29转换为八进制:
29 ÷ 8 = 3 ... 5
3 ÷ 8 = 0 ... 3
所以,29的八进制表示为35。
2.6十进制-十六进制转换
下面是将十进制转换为十六进制的步骤:
1. 将给定的十进制数除以16,得到商和余数。
2. 如果商大于0,将商继续除以16,重复这个过程,直到商为0。
3. 用余数来代表十六进制的数位。对于余数大于9的情况,使用A-F的字母来代表数字10-15。
4. 将得到的余数按照从右到左的顺序排列起来,得到的就是对应的十六进制数。
举个例子,将十进制数123转换为十六进制数:
1. 首先,将123除以16,得到商和余数。123÷16 = 7 余 11,也就是7B。
2. 商为7,继续除以16。7÷16 = 0 余 7,也就是07。
3. 将得到的两个余数按照从右到左的顺序排列起来,得到最终的结果为07B。
因此,十进制数123转换为十六进制数为07B。
2.7小数部分转换
进制间小数部分的转换是通过不断乘以目标进制的方式进行的。
以将十进制小数转换为二进制小数为例,首先将十进制小数乘以2,得到的整数部分即为二进制小数的第一位数。将余下的小数部分再次乘以2,得到的整数部分即为二进制小数的第二位数。依此类推,直到小数部分为0或者达到所需的精度为止。
例如,将十进制小数0.625转换为二进制小数,过程如下:
0.625 * 2 = 1.25,整数部分为1,余下的小数部分为0.25
0.25 * 2 = 0.5,整数部分为0,余下的小数部分为0.5
0.5 * 2 = 1.0,整数部分为1,小数部分为0,转换结束。
因此,0.625的二进制表示为0.101。
同样地,将二进制小数转换为其他进制的小数时,也是通过类似的方式进行的。不断乘以目标进制,每次得到的整数部分就是目标进制下的小数位数。
需要注意的是,在进行进制转换时,可能存在精度丢失的问题,因为不是所有的小数都能用某个进制的有限位数精确表示。
一个经典的进制转换中的精度丢失案例是十进制转换为二进制。在进行十进制到二进制的转换时,可能会遇到精度丢失的问题。
举个例子,假设我们有一个十进制数值1.1,想要将其转换为二进制。首先我们将1.1乘以2,得到2.2。整数部分为2,所以我们将其记录下来。然后将小数部分0.2再乘以2,得到0.4。同样地,我们记录下整数部分0。再将小数部分0.4乘以2,得到0.8,同样记录下整数部分0。这样继续下去,直到小数部分为0或者达到我们设定的精度。
然而,1.1在二进制中并不是一个有限的小数,它是一个循环小数,即1.1对应的二进制表示是无限循环的。在上述的转换过程中,由于计算机的存储精度限制,只能记录有限位数的二进制表示。因此,它最终会截断循环部分,导致精度丢失。
所以,当要进行进制转换时,特别是涉及到无限循环小数的情况,可能会出现精度丢失的问题。
相关文章:

嵌入式-数据进制之间的转换
目录 一.简介 1.1十进制 1.2二进制 1.3八进制 1.4十六进制 二.进制转换 2.1二进制-十进制转换 2.2八进制-十进制转换 2.3十六进制-十进制转换 2.4十进制-二进制转换 2.5十进制-八进制转换 2.6十进制-十六进制转换 2.7小数部分转换 一.简介 被传入到计算机的数据要…...
腾讯mini项目-【指标监控服务重构】2023-08-20
今日已办 PPT制作 答辩流程 概述:对项目背景、架构进行介绍(体现我们分组的区别和需求)人员:小组成员进行简短的自我介绍和在项目中的定位,分工进展:对项目进展介绍,其中a、b两组的区别和工作…...
智能文本纠错API的应用与工作原理解析
引言 在数字时代,文本撰写和传播变得日益重要,无论是在学校里写论文、在职场中发送邮件,还是在社交媒体上发表观点。然而,文字错误、标点符号错误、语法问题和不当的表达常常会削弱文本的质量,降低信息传达的效果。为…...

在springboot下将mybatis升级为mybatis-plus
在springboot下将mybatis升级为mybatis-plus 1. 整体描述2. 具体步骤2.1 更新pom引用2.2 更新yml配置2.3 更新config配置2.4 BaseEntity修改 3. 程序启动4. 总结 1. 整体描述 之前项目工程用的是mybatis,现在需要将其替换为mybatis-plus,mybatis-plus的…...
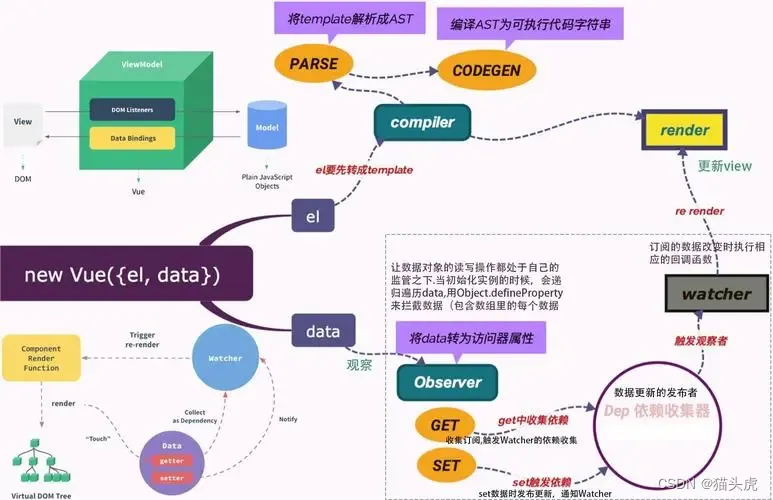
Vuex详解:Vue.js的状态管理方案
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
栈与队列经典题目——用队列实现栈
本篇文章讲解栈和队列这一部分知识点的经典题目:用栈实现队列、用队列实现栈。对应的题号分别为:Leetcode.225——用队列实现栈,。 在对两个题目进行解释之前,先回顾以下栈和队列的特点与不同: 栈是一种特殊的线性表…...
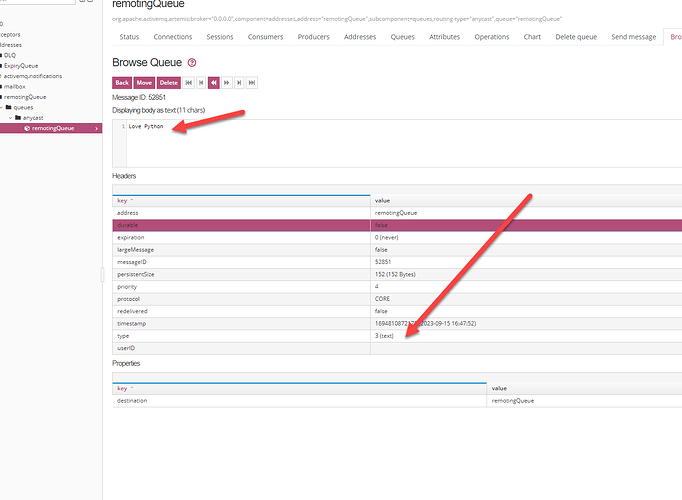
Python stomp 发送消息无法显示文本
我们向消息服务器通过 stomp 发送的是文本消息。 当消息服务器发送成功后,消息服务器上的文本没有显示,显示的是 2 进制的数据。 如上图,消息没有作为文本来显示。 问题和解决 消息服务器是如何判断发送的小时是文本还是二进制的。 根据官…...
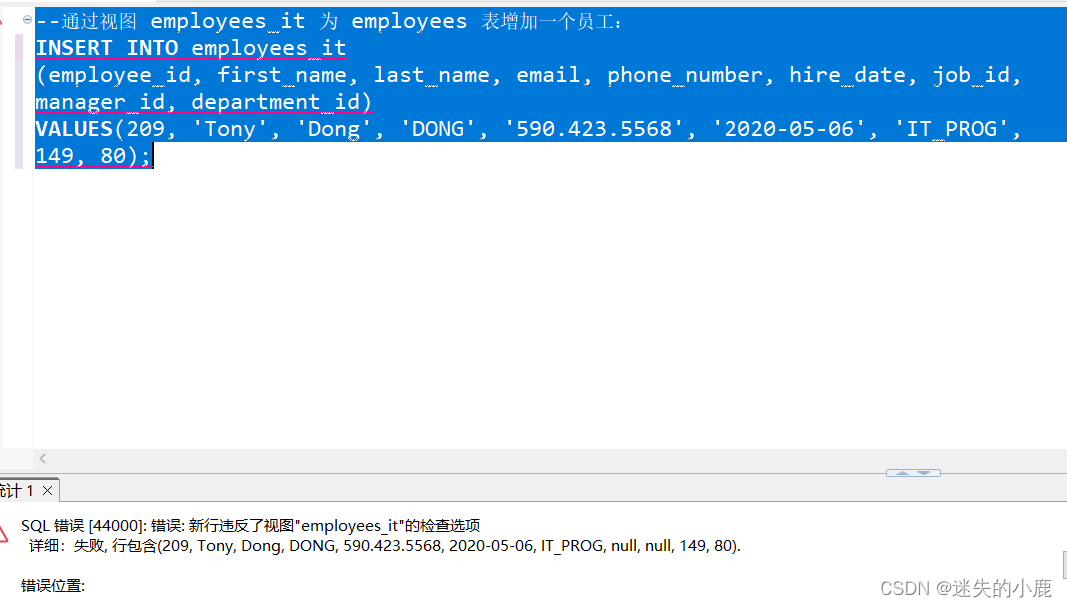
postgresql-视图
postgresql-视图 视图概述使用视图的好处 创建视图修改视图删除视图递归视图可更新视图WITH CHECK OPTION 视图概述 视图(View)本质上是一个存储在数据库中的查询语句。视图本身不包含数据,也被称为 虚拟表。我们在创建视图时给它指定了一个…...

科技资讯|Vision Pro头显无损音频仅限USB-C AirPods Pro 2耳机
彭博社的马克・古尔曼在最新发布的推文中表示,苹果 Vision Pro 头显的无损音频仅限于 USB-C AirPods Pro 2 耳机。 新款采用 USB-C 的 AirPods Pro 2 升级到了 IP54 级别(原版不防尘,仅 IPX4 级抗水),可陪伴用户在恶劣…...
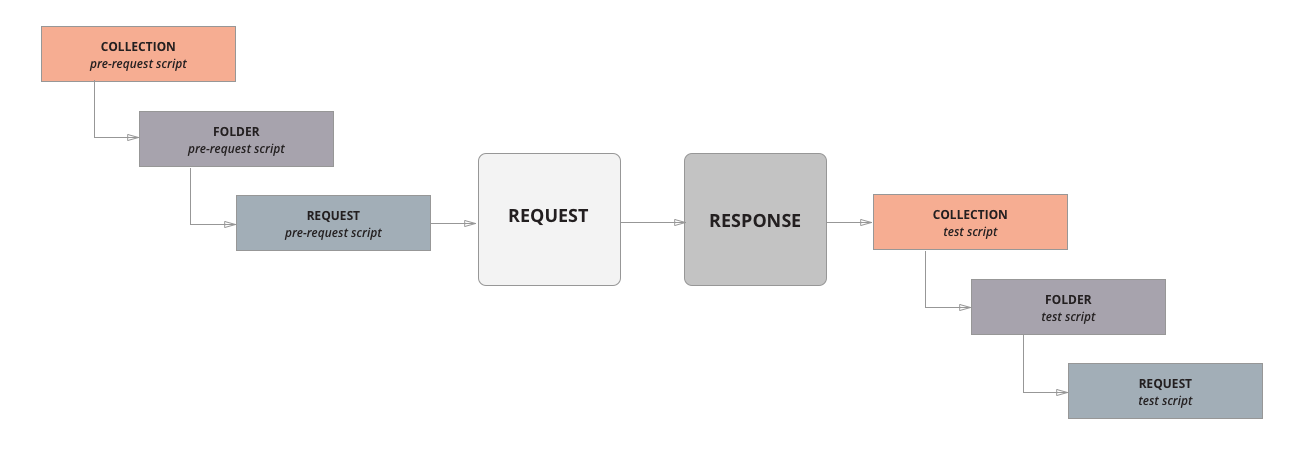
Postman应用——初步了解postman
Postman 是一个用于构建和使用 API 的 API 平台,Postman 简化了 API 生命周期的每个步骤并简化了协作,可以更快地创建更好的 API。 Postman 包含一个基于Node.js的强大的运行时,允许您向请求(request)和分组ÿ…...

分析报告显示,PHP是编程语言主力军,且在电商领域占据“统治地位”
日前有有业内专家透露了PHP语言的使用数据,并强调了PHP语言对于互联网的作用。 而根据W3 Techs发布的《全球前1000万个网站使用的编程语言分析(截至 2023.8)》中,有这样一组数据引起广泛的关注。PHP占比 77.2%、ASP占比 6.9%、Ruby 占比5.4%。 此外&am…...
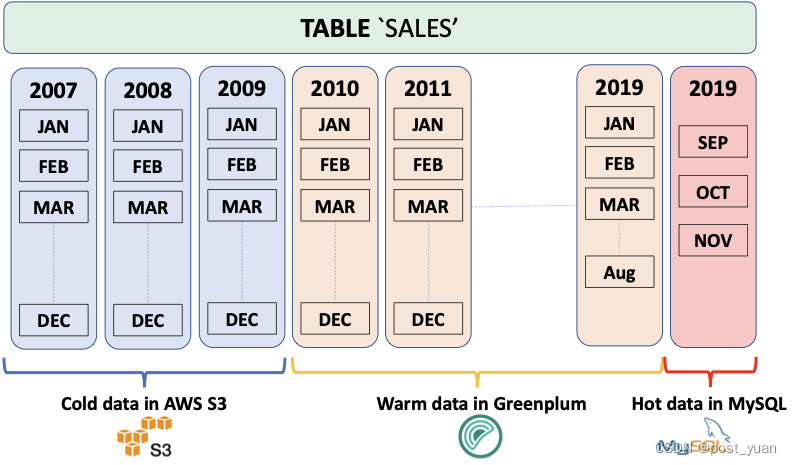
关于Greenplum Platform Extension Framework(PXF)
本文翻译自 https://docs.vmware.com/en/VMware-Greenplum-Platform-Extension-Framework/6.6/greenplum-platform-extension-framework/overview_pxf.html 随着数据存储和云服务的爆炸式增长,数据现在以各种格式驻留在许多不同的系统中。通常,数据根据…...

编程获取图像中的圆半径
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 即将推出EmguCV的教程,请大家还稍作等待。 之前网友咨询如何获得图像中圆形的半径,其中有两个十字作为标定…...

什么是Scrum?如何实施Scrum(敏捷开发)以及敏捷工具
什么是Scrum? Scrum是一个敏捷开发框架,它是一个增量的、迭代的开发过程。它被广泛应用于敏捷软件开发,在Scrum中,开发过程由若干个短的迭代周期组成,每个迭代周期称为一个Sprint。 那么Scrum如何实施呢…...
提升运营效率:仓储可视化的实时监控与优化
当今,仓储管理已经不再是简单的储存和分发商品的过程。随着供应链的复杂性增加,企业需要更高效的方式来管理和优化其仓储运营。在这个背景下,仓储可视化成为了一项关键的技术,它利用先进的数字化工具和数据分析来提升仓储管理的效…...
)
代理模式和单一职责原理一文读懂(设计模式与开发实践 P6)
文章目录 代理模式实现保护代理虚拟代理单一职责原理代理和本体 - 接口一致性虚拟代理 - 合并请求缓存代理其他代理 代理模式 定义:为一个对象提供一个代用品 & 占位符,以便 控制对他的访问 关键:不方便直接访问某个对象或不满足需要的时…...
Linux网络编程|TCP编程
一.网络基础 1.1网络发展史 Internet-“冷战”的产物 1957年10月和11月,前苏联先后有两颗“Sputnik”卫星上天 1958年美国总统艾森豪威尔向美国国会提出建立DARPA (Defense Advanced Research Project Agency),即国防部高级研究计划署&#…...
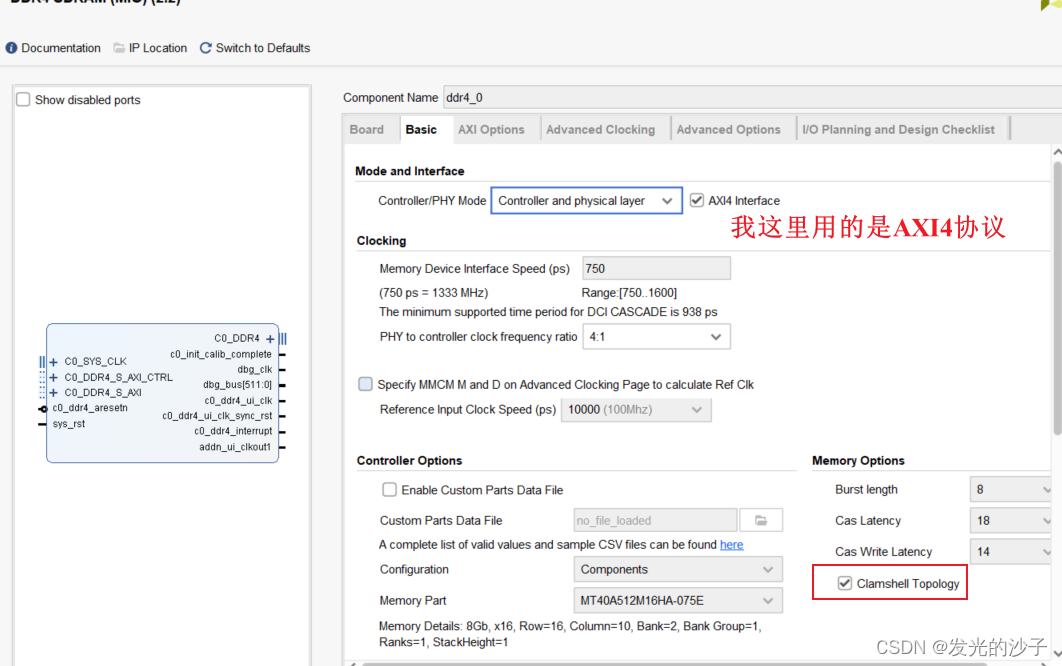
FPGA----VCU128的DDR4无法使用问题(全网唯一)
1、在Vivado 2019.1版本中使用DDR4的IP核会遇到如下图所示的错误,即便过了implementation生成了bit,DDR4也无法正常启动。 2、解决办法,上xilinx社区搜一下就知道了 AMD Customer Communityhttps://support.xilinx.com/s/article/69035?lan…...
【毕设选题】flink大数据淘宝用户行为数据实时分析与可视化
文章目录 0 前言1、环境准备1.1 flink 下载相关 jar 包1.2 生成 kafka 数据1.3 开发前的三个小 tip 2、flink-sql 客户端编写运行 sql2.1 创建 kafka 数据源表2.2 指标统计:每小时成交量2.2.1 创建 es 结果表, 存放每小时的成交量2.2.2 执行 sql &#x…...
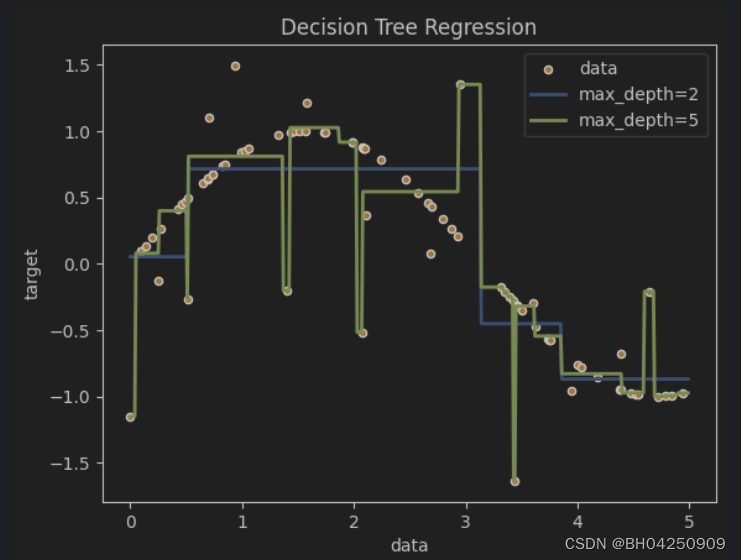
机器学习练习-决策树
机器学习练习-决策树 代码更新地址:https://github.com/fengdu78/WZU-machine-learning-course 代码修改并注释:黄海广,haiguang2000wzu.edu.cn 1.分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
