【力扣1462】课程表(拓扑排序+bitset优化到O(n))
题目描述:
你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。
- 有的课会有直接的先修课程,比如如果想上课程
1,你必须先上课程0,那么会以[0,1]数对的形式给出先修课程数对。
先决条件也可以是 间接 的。如果课程 a 是课程 b 的先决条件,课程 b 是课程 c 的先决条件,那么课程 a 就是课程 c 的先决条件。
你也得到一个数组 queries ,其中 queries[j] = [uj, vj]。对于第 j 个查询,您应该回答课程 uj 是否是课程 vj 的先决条件。
返回一个布尔数组 answer ,其中 answer[j] 是第 j 个查询的答案。
示例 1:

输入:numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] 输出:[false,true] 解释:课程 0 不是课程 1 的先修课程,但课程 1 是课程 0 的先修课程。
示例 2:
输入:numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] 输出:[true,true]
数据范围:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= n - 1ai != bi- 每一对
[ai, bi]都 不同 - 先修课程图中没有环。
1 <= queries.length <= 1040 <= ui, vi <= n - 1ui != vi
分析思路:
首先看样例的图,大概率是图论题,再一个题目中有很明显的先后关系,所以可以锁定这个题是一道拓扑排序题。 当然这个题范围很小 n是100,Floyd的3层循环好像也能求解(类似传递闭包),代码应该更容易实现。 不过我想用bitset实现,那样的话 数据n如果开1e4(10000) 也没事, bitset的空间复杂度是(n*n/64).
AC的过程还是有点艰难,之前写题没怎么用过vector,刚才初始化少加1 看了半天 o.O。
因为题目编号范围是0~n-1,不太习惯,怕0这个数字会未知错误, 所以我给所有的编号都进行了+1处理
f[x][y]为1 表示x->y有边; 为0 表示无边
class Solution {
public:vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<int>d(numCourses+1);vector<vector<int>> edge(numCourses+1);for(vector<int> x:prerequisites){edge[x[0]+1].push_back(x[1]+1);//建边d[x[1]+1]++; //处理入度}queue<int>q;for(int i=1;i<=numCourses;i++){if(!d[i]){q.push(i);}}vector<int>ans;//ans里面存的是拓扑序列,注意:拓扑序列不是唯一的while(q.size()){int t=q.front();q.pop();ans.push_back(t);for(int x:edge[t]){if(--d[x]==0){q.push(x);}}}bitset<110>f[numCourses+1];for(int i=numCourses-1;i>=0;i--){int x=ans[i];for(int y:edge[x]){f[x][y]=1;f[x]|=f[y];//相当于位运算,时间复杂度是O(1)}}//处理答案vector<bool>ans1;for(auto x:queries){if(f[x[0]+1][x[1]+1])ans1.push_back(1);else ans1.push_back(0);}return ans1;}
};相关文章:

【力扣1462】课程表(拓扑排序+bitset优化到O(n))
题目描述: 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。 有的课会有直接的先修课程&am…...
【AI】机器学习——支持向量机(非线性及分析)
5. 支持向量机(线性SVM) 文章目录 5.4 非线性可分SVM5.4.1 非线性可分问题处理思路核技巧核函数特点 核函数作用于SVM 5.4.2 正定核函数由 K ( x , z ) K(x,z) K(x,z) 构造 H \mathcal{H} H 空间步骤 常用核函数 5.5 SVM参数求解算法5.6 SVM与线性模型关系 5.4 非线性可分SVM …...
2023-09-20 LeetCode每日一题(拿硬币)
2023-09-20每日一题 一、题目编号 LCP 06. 拿硬币二、题目链接 点击跳转到题目位置 三、题目描述 桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。 示…...
Java21的新特性
Java语言特性系列 Java5的新特性Java6的新特性Java7的新特性Java8的新特性Java9的新特性Java10的新特性Java11的新特性Java12的新特性Java13的新特性Java14的新特性Java15的新特性Java16的新特性Java17的新特性Java18的新特性Java19的新特性Java20的新特性Java21的新特性Java22…...
测试-----selenuim webDriver
文章目录 1.页面导航2.元素定位3. 浏览器操作4.获取元素信息5. 鼠标的操作6. 键盘操作7. 元素等待8.下拉框9.弹出框10.滚动条11.frame处理12.验证码处理(cookie) 1.页面导航 首先是导入对应的包 :from selenium import webdriver然后实例化:driver web…...

21天学会C++:Day12----初始化列表
CSDN的uu们,大家好。这里是C入门的第十一讲。 座右铭:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:C专题 目录 1. 初始化列表 1.1 引入 1.2 初始化列表 1.3 初始化列表的注意事项 1.…...
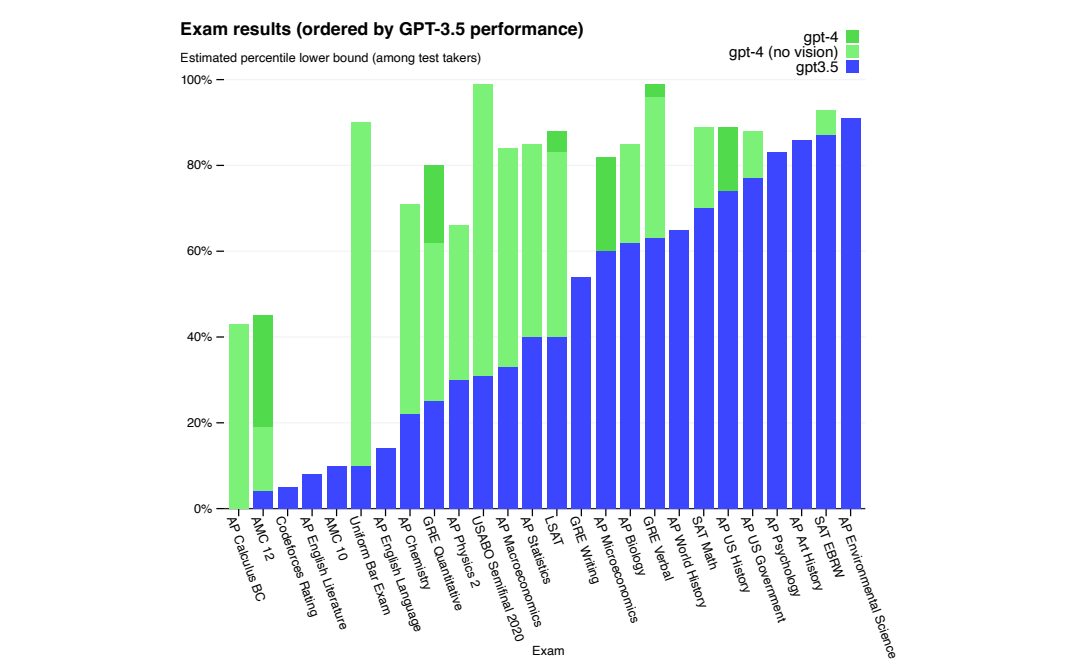
OpenAI开发系列(二):大语言模型发展史及Transformer架构详解
全文共1.8w余字,预计阅读时间约60分钟 | 满满干货,建议收藏! 一、介绍 在2020年秋季,GPT-3因其在社交媒体上病毒式的传播而引发了广泛关注。这款拥有超过1.75亿参数和每秒运行成本达到100万美元的大型语言模型(Large …...

Gson - 一个Java序列化/反序列化库
官网 GitHub - google/gson: A Java serialization/deserialization library to convert Java Objects into JSON and back 项目简介 一个Java序列化/反序列化库,用于将Java对象转换为JSON和返回JSON。 Gson is a Java library that can be used to convert Java…...
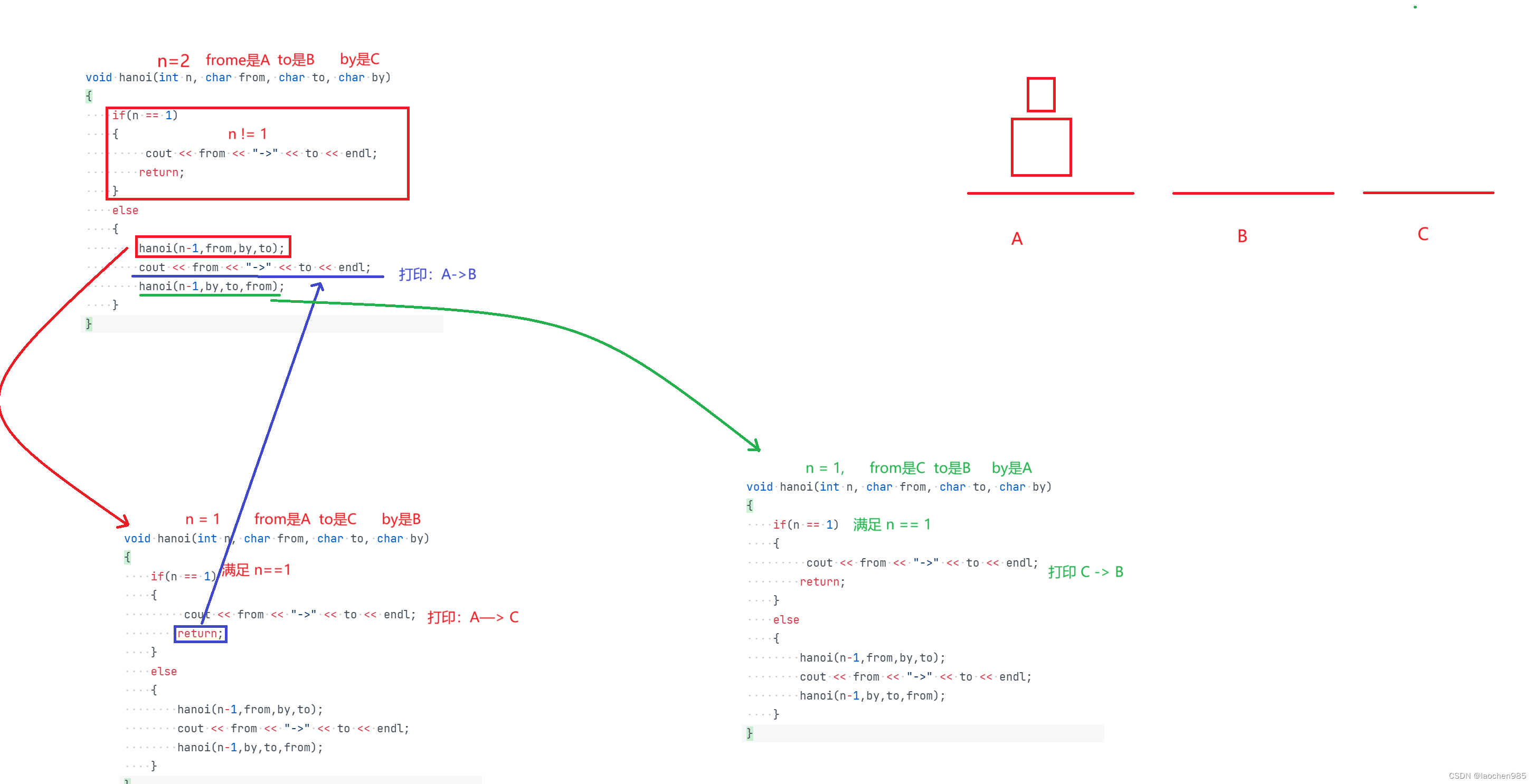
6-1 汉诺塔
汉诺(Hanoi)塔问题是一个经典的递归问题。 设有A、B、C三个塔座;开始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上,并仍按同样顺序叠放。在…...
添加密码登录验证)
Linux之initd管理系统(海思、ZYNQ、复旦微)添加密码登录验证
设置root用户密码:passwd命令设置密码,即修改/etc/passwd文件 一、串口提示输入用户名密码方法 修改 /etc/inittab 方法一: 增加: ::askfirst:-/bin/login 注释: #::respawn:/sbin/getty -L ttyS000 115200 vt…...
怎么更改代理ip,代理ip如何切换使用?
我们要如何使用HTTP代理,对它进行切换使用呢? 如果你购买了青果网络的HTTP代理,可以在文档这边获取使用方法: 可以在这里调试: 也可以在这里选择key提取。 如果有的朋友们想利用利用python,每隔30秒使用API…...
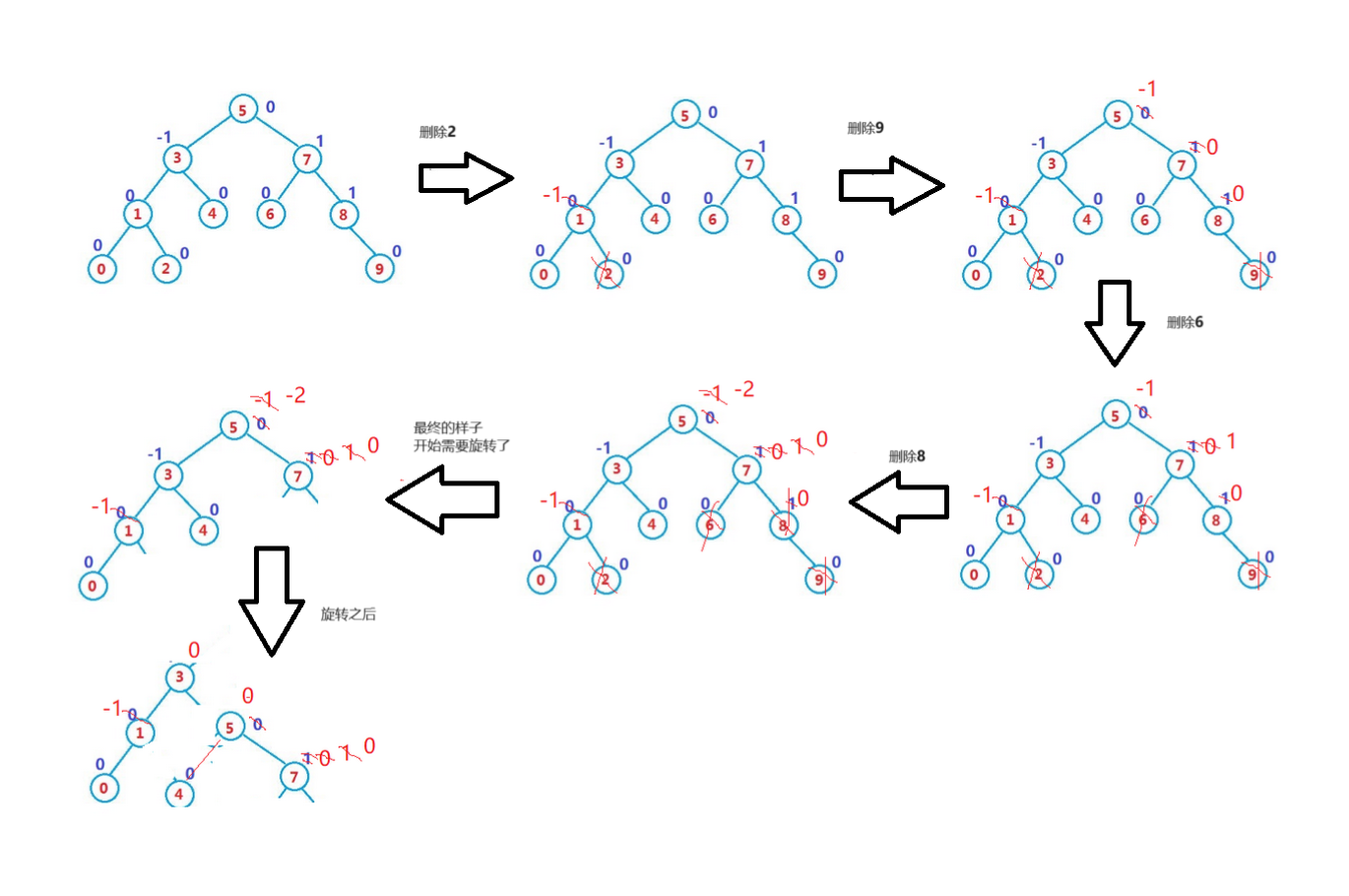
【C++从0到王者】第三十三站:AVL树
文章目录 前言一、AVL 树的概念二、AVL树的实现1. AVL树的结点定义2. AVL树的插入之插入部分3. AVL树的插入之平衡因子的改变4. AVL树的插入之左旋5. AVL树的左旋抽象图6.AVL树的右旋抽象图7. AVL树的双旋8. AVL树的右左双旋9. AVL树的右左双旋的本质10. AVL树的左右双旋11. AV…...

手机机型响应式设置2
window.screen.height:屏幕高度 window.innerHeight:视口高度(去除浏览器头尾的高度) document.body.clientHeight:内容高度 vh:网页视口高度的1/100 vw:网页视口宽度的1/100 vmaxÿ…...

uni-app 之 解决u-button始终居中问题
uView中u-button始终居中问题如何解决的简单方法? 1:给该元素margin-right: 0;可以达到向右靠齐; 2:给该元素的父元素设置float: right image.png <u-button style"width: 50px; margin-left: 0;" plain"t…...

Python日期处理库:掌握时间的艺术
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 日期和时间在计算机编程…...

JOSEF约瑟 智能电流继电器KWJL-20/L KWLD26 零序孔径45mm 柜内导轨式安装
KWJL-20智能电流继电器 零序互感器: KWLD80 KWLD45 KWLD26 KWJL-20 一、产品概述 KWJL-20系列智能剩余电流继电器(以下简称继电器)适用于交流电压至660V或更高的TN、TT、和IT系统,频率为50Hz。通过零序电流互感器检测出超过…...

NLP技术如何为搜索引擎赋能
目录 1. NLP关键词提取与匹配在搜索引擎中的应用1. 关键词提取例子 2. 关键词匹配例子 Python实现 2. NLP语义搜索在搜索引擎中的应用1. 语义搜索的定义例子 2. 语义搜索的重要性例子 Python/PyTorch实现 3. NLP个性化搜索建议在搜索引擎中的应用1. 个性化搜索建议的定义例子 2…...

演唱会没买到票?VR直播为你弥补遗憾
听说周杰伦开了演唱会?没买到票的人是不是有着大大的遗憾呢?很多时候大型活动、演唱会都会因为场地限制而导致很多人未能有缘得见,而且加上票价成本高,“黄牛票”事件频出,我们的钱包受不住啊!!…...

myabtis的缓存级别
文章目录 MyBatis缓存的区别是什么作用范围方面有哪些差异生命周期数据进行了存储缓存的优缺点 MyBatis缓存的区别是什么 MyBatis 提供了一级缓存和二级缓存,这两者的主要区别在于其作用范围和生命周期。 一级缓存:一级缓存是 SqlSession 级别的缓存。…...
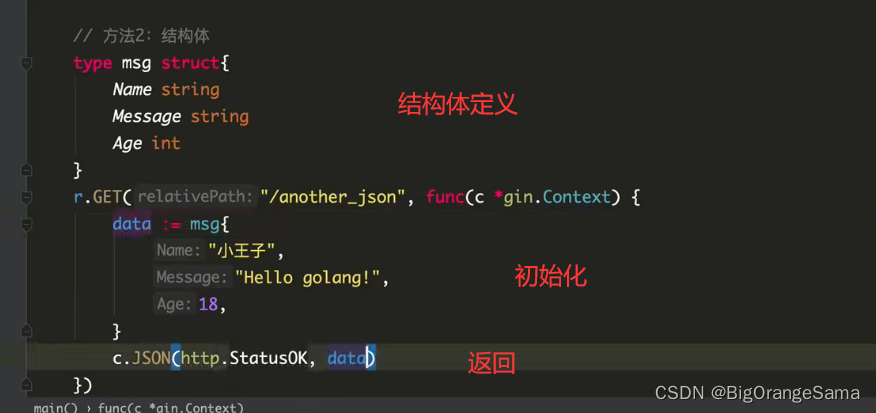
gin框架再探
Gin框架介绍及使用 | 李文周的博客 (liwenzhou.com) lesson03_gin框架初识_哔哩哔哩_bilibili 1.路由引擎 //路由引擎 rgin.Default() 2.一些http请求方法 get post put delete等等 遇到什么路径,执行什么函数 r.GET("/hello",func{做你想做的事返回…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...

Linux系统:进程间通信-匿名与命名管道
本节重点 匿名管道的概念与原理匿名管道的创建命名管道的概念与原理命名管道的创建两者的差异与联系命名管道实现EchoServer 一、管道 管道(Pipe)是一种进程间通信(IPC, Inter-Process Communication)机制,用于在不…...
