【考研数学】线性代数第五章 —— 特征值和特征向量(3,矩阵对角化理论)
文章目录
- 引言
- 三、矩阵对角化理论
- 3.1 一般矩阵的相似对角化
- 3.2 实对称矩阵的相似对角化
- 3.2.1 实对称矩阵相似对角化定理
- 3.2.2 实对称矩阵相似对角化过程
- 写在最后
引言
承接前文,我们来看看矩阵的对角化理论。
我们前面提到对角化是在矩阵相似那里,若存在可逆矩阵 P P P ,使得 P − 1 A P = Λ P^{-1}AP=\Lambda P−1AP=Λ ,其中 Λ \Lambda Λ 为对角矩阵,则称 A A A 可以相似对角化。
三、矩阵对角化理论
3.1 一般矩阵的相似对角化
设 A \pmb{A} A 为 n n n 阶矩阵,其特征值为 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn ,若存在可逆矩阵 P \pmb{P} P ,使得 P − 1 A P = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] , \pmb{P}^{-1}\pmb{AP}=\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}, P−1AP= λ10⋮00λ2⋮0⋯⋯⋯00⋮λn , 称矩阵 A \pmb{A} A 可相似对角化,或 A \pmb{A} A 可对角化,或与对角矩阵相似。
第一步: 由特征方程 ∣ λ E − A ∣ = 0 |\lambda\pmb{E}-\pmb{A}|=0 ∣λE−A∣=0 ,求出矩阵 A \pmb{A} A 的特征值 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn ;
第二步: 求齐次线性方程组 ( λ i E − A ) X = 0 ( 1 ≤ i ≤ n ) (\lambda_i\pmb{E}-\pmb{A})\pmb{X}=\pmb{0}(1\leq i \leq n) (λiE−A)X=0(1≤i≤n) 的基础解系,进而求出矩阵 A \pmb{A} A 的线性无关的特征向量 α 1 , α 2 , ⋯ , α m \pmb{\alpha_1,\alpha_2,\cdots,\alpha_m} α1,α2,⋯,αm ;
回忆一下:
1.设 r ( A ) = r < n r(A)=r<n r(A)=r<n ,则 A X = 0 \pmb{AX=0} AX=0 所有解构成的解向量组的极大线性无关组称为方程组 A X = 0 \pmb{AX=0} AX=0 的一个基础解系。基础解系中所含有的线性无关的解向量的个数为 ( n − r ) (n-r) (n−r) 个。具体求解方法见方程组那一篇文章,传松门 。
2.上一篇文章有定理 4:不同特征值对应的特征向量线性无关。
第三步:
(一)若 m = n m=n m=n ,则矩阵 A \pmb{A} A 可相似对角化,对角化过程如下:
有定理 5:设 A \pmb{A} A 为 n n n 阶矩阵,则 A \pmb{A} A 可相似对角化(或与对角矩阵相似)的充分必要条件是 A \pmb{A} A 有 n n n 个线性无关的特征向量。
令 P = ( α 1 , α 2 , ⋯ , α n ) \pmb{P}=(\pmb{\alpha_1,\alpha_2,\cdots,\alpha_n}) P=(α1,α2,⋯,αn) ,显然 P \pmb{P} P 可逆。
列向量组线性无关,则矩阵满秩,自然是可逆的。
由 A α 1 = λ 1 α 1 , A α 2 = λ 2 α 2 , ⋯ , A α n = λ n α n \pmb{A\alpha_1}=\lambda_1\pmb{\alpha_1},\pmb{A\alpha_2}=\lambda_2\pmb{\alpha_2},\cdots,\pmb{A\alpha_n}=\lambda_n\pmb{\alpha_n} Aα1=λ1α1,Aα2=λ2α2,⋯,Aαn=λnαn 得: A P = ( A α 1 , A α 2 , ⋯ , A α n ) = ( λ 1 α 1 , λ 2 α 2 , ⋯ , λ n α n ) = P [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] , \pmb{AP}=(\pmb{A\alpha_1,A\alpha_2,\cdots,A\alpha_n})=(\lambda_1\pmb{\alpha_1},\lambda_2\pmb{\alpha_2},\cdots,\lambda_n\pmb{\alpha_n})=\pmb{P}\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}, AP=(Aα1,Aα2,⋯,Aαn)=(λ1α1,λ2α2,⋯,λnαn)=P λ10⋮00λ2⋮0⋯⋯⋯00⋮λn , 两边同时左乘以 P − 1 \pmb{P^{-1}} P−1 ,有 P − 1 A P = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] . \pmb{P}^{-1}\pmb{AP}=\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}. P−1AP= λ10⋮00λ2⋮0⋯⋯⋯00⋮λn .
(二)若 m < n m<n m<n ,则矩阵 A \pmb{A} A 不可相似对角化。
3.2 实对称矩阵的相似对角化
3.2.1 实对称矩阵相似对角化定理
定理 1 —— 若 A T = A \pmb{A}^T=\pmb{A} AT=A ,则 A \pmb{A} A 一定可以相似对角化。
定理 2 —— 设 A T = A \pmb{A}^T=\pmb{A} AT=A ,则存在正交矩阵 Q \pmb{Q} Q ,使得 Q T A Q = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] . \pmb{Q}^T\pmb{AQ}=\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}. QTAQ= λ10⋮00λ2⋮0⋯⋯⋯00⋮λn .
3.2.2 实对称矩阵相似对角化过程
第一步: 由特征方程 ∣ λ E − A ∣ = 0 |\lambda\pmb{E}-\pmb{A}|=0 ∣λE−A∣=0 ,求出矩阵 A \pmb{A} A 的特征值 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn ;
第二步: 求齐次线性方程组 ( λ i E − A ) X = 0 ( 1 ≤ i ≤ n ) (\lambda_i\pmb{E}-\pmb{A})\pmb{X}=\pmb{0}(1\leq i \leq n) (λiE−A)X=0(1≤i≤n) 的基础解系,进而求出矩阵 A \pmb{A} A 的线性无关的特征向量 α 1 , α 2 , ⋯ , α n \pmb{\alpha_1,\alpha_2,\cdots,\alpha_n} α1,α2,⋯,αn ;
第三步:
(一)找可逆矩阵 P \pmb{P} P ,按照上述一般矩阵对角化过程进行:
令 P = ( α 1 , α 2 , ⋯ , α n ) \pmb{P}=(\pmb{\alpha_1,\alpha_2,\cdots,\alpha_n}) P=(α1,α2,⋯,αn) ,显然 P \pmb{P} P 可逆。
由 A α 1 = λ 1 α 1 , A α 2 = λ 2 α 2 , ⋯ , A α n = λ n α n \pmb{A\alpha_1}=\lambda_1\pmb{\alpha_1},\pmb{A\alpha_2}=\lambda_2\pmb{\alpha_2},\cdots,\pmb{A\alpha_n}=\lambda_n\pmb{\alpha_n} Aα1=λ1α1,Aα2=λ2α2,⋯,Aαn=λnαn 得: A P = ( A α 1 , A α 2 , ⋯ , A α n ) = ( λ 1 α 1 , λ 2 α 2 , ⋯ , λ n α n ) = P [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] , \pmb{AP}=(\pmb{A\alpha_1,A\alpha_2,\cdots,A\alpha_n})=(\lambda_1\pmb{\alpha_1},\lambda_2\pmb{\alpha_2},\cdots,\lambda_n\pmb{\alpha_n})=\pmb{P}\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}, AP=(Aα1,Aα2,⋯,Aαn)=(λ1α1,λ2α2,⋯,λnαn)=P λ10⋮00λ2⋮0⋯⋯⋯00⋮λn , 两边同时左乘以 P − 1 \pmb{P^{-1}} P−1 ,有 P − 1 A P = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] . \pmb{P}^{-1}\pmb{AP}=\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}. P−1AP= λ10⋮00λ2⋮0⋯⋯⋯00⋮λn .
(二)找正交矩阵 Q \pmb{Q} Q ,使得 Q T A Q \pmb{Q}^T\pmb{AQ} QTAQ 为对角矩阵的过程如下:
(1)将 α 1 , α 2 , ⋯ , α n \pmb{\alpha_1,\alpha_2,\cdots,\alpha_n} α1,α2,⋯,αn 进行施密特正交化为 β 1 , β 2 , ⋯ , β n \pmb{\beta_1,\beta_2,\cdots,\beta_n} β1,β2,⋯,βn ;
(2)将 β 1 , β 2 , ⋯ , β n \pmb{\beta_1,\beta_2,\cdots,\beta_n} β1,β2,⋯,βn 规范化为 γ 1 , γ 2 , ⋯ , γ n \pmb{\gamma_1,\gamma_2,\cdots,\gamma_n} γ1,γ2,⋯,γn 。令 Q = ( γ 1 , γ 2 , ⋯ , γ n ) \pmb{Q=(\gamma_1,\gamma_2,\cdots,\gamma_n}) Q=(γ1,γ2,⋯,γn) ,显然 Q \pmb{Q} Q 为正交矩阵。实对称矩阵特征向量进行施密特正交化后,仍然为特征向量,因此有 A γ 1 = λ 1 γ 1 , A γ 2 = λ 2 γ 2 , ⋯ , A γ n = λ n γ n \pmb{A\gamma_1}=\lambda_1\pmb{\gamma_1},\pmb{A\gamma_2}=\lambda_2\pmb{\gamma_2},\cdots,\pmb{A\gamma_n}=\lambda_n\pmb{\gamma_n} Aγ1=λ1γ1,Aγ2=λ2γ2,⋯,Aγn=λnγn 得: A Q = Q [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] , \pmb{AQ}=\pmb{Q}\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}, AQ=Q λ10⋮00λ2⋮0⋯⋯⋯00⋮λn , 两边同时左乘以 Q T \pmb{Q^{T}} QT ,有 Q T A Q = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ λ n ] . \pmb{Q}^{T}\pmb{AQ}=\begin{bmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{bmatrix}. QTAQ= λ10⋮00λ2⋮0⋯⋯⋯00⋮λn .
一般矩阵,不一定能相似对角化,要求有 n n n 个线性无关的特征向量才可以相似对角化。
实对称矩阵的不同特征值对应的特征向量本来就是正交的,之所以还要正交规范化,是为了求一个正交矩阵。
下面是一些笔记注解:
- 若矩阵 A \pmb{A} A 的特征值都是单值,则 A \pmb{A} A 一定可以相似对角化。
- 若 A \pmb{A} A 为实对称矩阵,则 A \pmb{A} A 一定可以相似对角化。
- 若 n n n 阶矩阵 A \pmb{A} A 有 n n n 个线性无关的特征向量,则 A \pmb{A} A 一定可以相似对角化。
- 若矩阵 A \pmb{A} A 的每个特征值的重数与其对应的线性无关的特征向量的个数相同时, A \pmb{A} A 一定可以相似对角化。
- 若 A \pmb{A} A 至少有一个特征值,其重数与其对应的线性无关的特征向量的个数不同时, A \pmb{A} A 一定不能相似对角化。
- 若 A \pmb{A} A 不是实对称矩阵,则 A \pmb{A} A 在相似对角化的过程中,不可对特征向量进行正交规范化。因为有可能正交规范后就不是特征向量了。
写在最后
这一块内容刚接触可太费头脑了,而且一定是需要大量练习题目的。
那到此,关于特征值和特征向量的理论部分告一段落了,最后只剩下一个二次型了。
相关文章:
)
【考研数学】线性代数第五章 —— 特征值和特征向量(3,矩阵对角化理论)
文章目录 引言三、矩阵对角化理论3.1 一般矩阵的相似对角化3.2 实对称矩阵的相似对角化3.2.1 实对称矩阵相似对角化定理3.2.2 实对称矩阵相似对角化过程 写在最后 引言 承接前文,我们来看看矩阵的对角化理论。 我们前面提到对角化是在矩阵相似那里,若存…...

【计算机网络】IP数据报首部格式、最大传输单元MTU、最大分段大小MSS
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 更多计算机网络知识专栏:计算机网络🔥 给大家跳段…...

shell脚本之文件读写
shell脚本之文件读写 1、读取文件内容并打印2、将内容写入文件3、追加内容到文件末尾4、读取文件内容到变量中5、逐行读取文件内容并处理6、逐行追加内容到文件末尾7、获取文件行数8、获取文件最后一个单词 Shell 脚本读写文件的方法有很多种,下面是一些常见的方法&…...
SAP 刷新Fiori Apps缓存的方法(解决修改CDS后Fiori无法重载新配置)
1. 问题 修改CDS Annotation后,基于Fiori Element发布的Fiori App无法应用新的界面 2. 解决办法 2319491 - How to clean up the cache after applying changes that affect SAP Fiori apps刷新Frontend: SE38: /UI5/APP_INDEX_CALCULATE…...
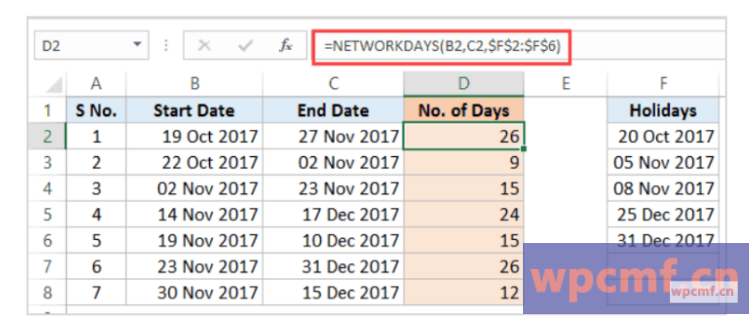
如何在 Excel 中计算日期之间的天数
计算两个日期之间的天数是 Excel中的常见操作。无论您是规划项目时间表、跟踪时间还是分析一段时间内的趋势,了解如何在 Excel 中查找日期之间的天数都可以提供强大的日期计算功能。 幸运的是,Excel 提供了多种简单的方法来获取两个日期之间的天数。继续…...

Java高级-注解
注解 1.介绍2.元注解3.注解的解析4.注解的应用场景 1.介绍 注解 Annotation 就是Java代码里的特殊标记,作用是让其他程序根据注解信息来决定什么是执行该程序注解:注解可以在类上、构造器上、方法上、成员变量上、参数上等位置 自定义注解 /*** 自定…...
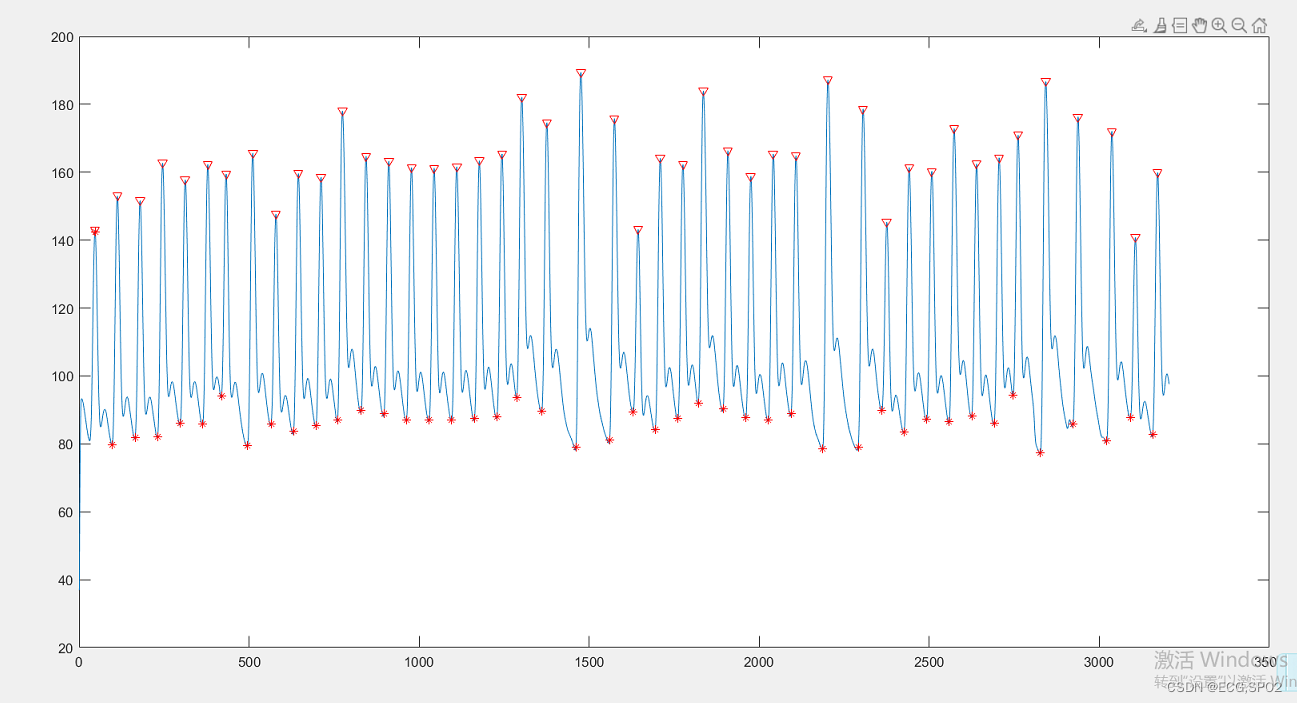
wabp.m 代码注释(便于算法快速理解)
算法效果: 波峰和起点检测效果: function [r,pk] = wabp(Araw, Offset,Scale, Fs) % r = wabp(Araw,Offset,Scale, Fs); % Input: Araw (125Hz sampled) waveform in wfdb-MIT format, % Offset, Scale % Araw = 血压波形 % Offset=偏移(信号减去或者加上偏移恢复成…...

数据库数据恢复-SQL SERVER数据库文件损坏的故障表现数据恢复方案
SQL SERVER数据库故障类型: SQL SERVER数据库MDF(NDF)或LDF损坏。 SQL SERVER数据库故障原因: 1、数据库正在操作过程中,机器突然断电。 2、人为误操作。 SQL SERVER数据库MDF(NDF)或LDF损坏的…...

flink中cpu消耗的大户-序列化和反序列化
背景 故事的起源来源于这样一篇关于序列化/反序列化优化的文章https://www.ververica.com/blog/a-journey-to-beating-flinks-sql-performance,当把传输的对象从String变成byte[]数组后,QPS直接提升了50% flink的网络数据交换优化 在flink中对于每个算子之间的跨…...

使用 K 均值聚类进行颜色分割
介绍 颜色分割是计算机视觉中使用的一种技术,用于根据颜色识别和区分图像中的不同对象或区域。聚类算法可以自动将相似的颜色分组在一起,而不需要为每种颜色指定阈值。当处理具有大范围颜色的图像时,或者当事先不知道确切的阈值时,这非常有用。 在本教程中,我们将探讨如何…...
)
Redis 哈希表操作实战(全)
目录 HSET 添加 HSETNX 添加 HMSET 批量添加 HGET 获取元素 HGETALL 获取所有 HMGET 批量查询 HEXISTS 判断是否存在 HINCRBY 增加整数 HINCRBYFLOAT 添加浮点数 HLEN 查Field数量 HKEYS 查所有Field HVALS 查所有Field值 HSCAN 迭代 HDEL 删除Field HSET 添加 …...

element table合并行或列 span-method
首先来看下官网上如何写的 <template><div><el-table:data"tableData":span-method"objectSpanMethod"borderstyle"width: 100%; margin-top: 20px"><el-table-columnprop"id"label"ID"width"18…...
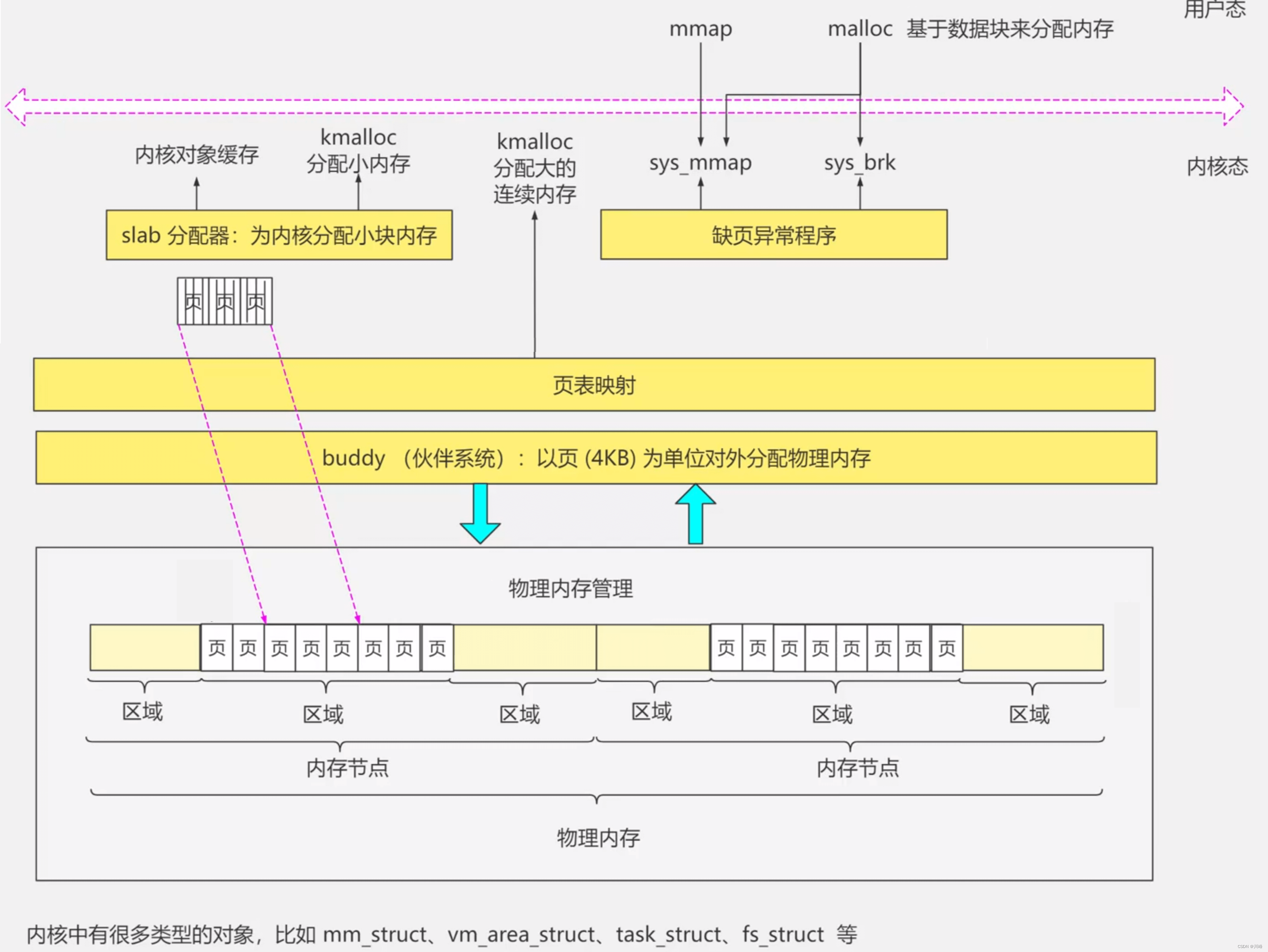
【操作系统笔记】内存分配
内存对齐 问题:为什么需要内存对齐呢? 主要原因是为了兼容,为了让程序可以运行在不同的处理器中,有很多处理器在访问内存的时候,只能从特定的内存地址读取数据。换个说法就是处理器每次只能从内存取出特定个数字节的数…...

Web 整合
HTML span 行内元素 p 块级元素 br/ 强制换行 i em倾斜 b strong 加粗 u 下划线 mark 高亮 超链接 a :a href"链接地址" target"_blank" alt"可替文本" title"文字提示" tartget:_self 自己界面打开 _…...

hasOwnProperty 方法解析
一、含义: hasOwnProperty 是 JavaScript 中的一个内置方法,用于检查对象是否具有指定名称的属性。 具体来说,hasOwnProperty 方法用于判断一个对象是否拥有某个指定的属性,而不是继承自原型链的属性。它是一个布尔值方法&#…...

使用 nohup 运行 Python 脚本
简介:在数据科学、Web 开发或者其他需要长时间运行的任务中,我们经常需要让 Python 脚本在后台运行。尤其是在远程服务器上,可能因为网络不稳定或需要执行多个任务,我们不希望 Python 脚本因为终端关闭而被终止。这时,…...
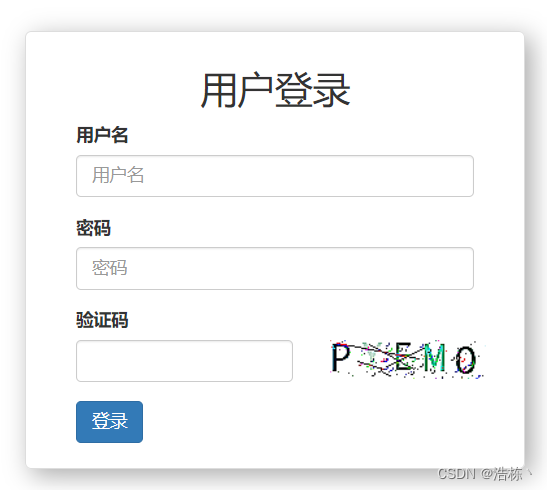
Django:五、登录界面实现动态图片验证码
一、下载包 pip install pillow 二、代码 这是一个函数,无输入,返回两个值。一个值是图片,一个值是图片中的数字及字母。 需要注意:font_fileMonaco.ttf 是一个验证码字体文件,如有需要,可三连私信。 …...
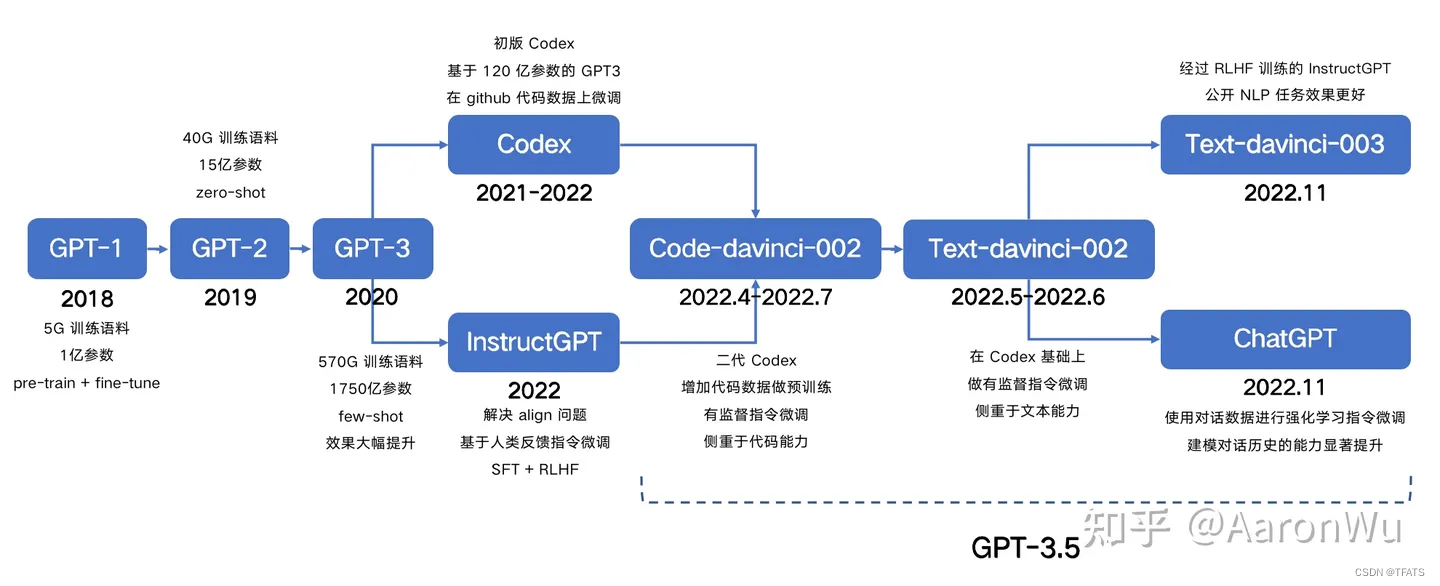
GPT,GPT-2,GPT-3,InstructGPT的进化之路
ChatGPT 火遍圈内外,突然之间,好多人开始想要了解 NLP 这个领域,想知道 ChatGPT 到底是个什么?作为在这个行业奋斗5年的从业者,真的很开心让人们知道有一群人在干着这么样的一件事情。这也是我结合各位大佬的文章&…...
)
firefox_dev_linux下载安装配置(部分系统自带包请看结尾)
download 从 Firefox 的官方网站下载 Firefox Developer Edition 的 tar 文件 firefox_dev_linux_download # 终端快速下载 wget https://download.mozilla.org/?productfirefox-devedition-latest-ssl&oslinux64&langen-US彻底删除自带原版 # apt系 sudo apt --pu…...
vim缓存-交换文件
Catf1agCTF靶场 web swp 题目链接:http://catf1ag.cn/ 个人博客:https://sword-blogs.com/ 题目考点: vim在编辑文档的过程中如果异常退出,会产生缓存文件 vim 交换文件名 参考文章:vim手册 https://yianwillis.…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
