数据结构学习笔记——查找算法中的树形查找(平衡二叉树)
目录
- 一、平衡二叉树的定义
- 二、平衡因子
- 三、平衡二叉树的插入和构造
- (一)LL型旋转
- (二)LR型旋转
- (三)RR型旋转
- (四)RL型旋转
- 四、平衡二叉树的删除
- (一)叶子结点
- (二)只有左/右子树,没有右/左子树
- (三)既有左子树,又有右子树
- 五、平衡二叉树的查找和平均查找长度
一、平衡二叉树的定义
平衡二叉树以二叉排序树为基础,若二叉排序树中左、右子树的高度之差的绝对值不超过1,则称为平衡二叉树(AVL树),其左、右子树也为一棵平衡二叉树,其平均查找长度为O(log2n),如下:
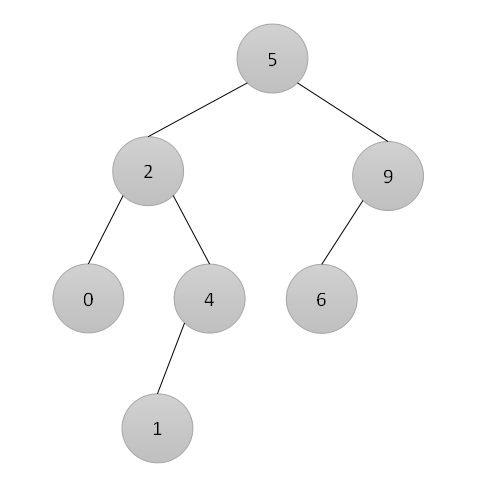
- 一棵具有 m 层的平衡二叉树(AVL),最多有2m-1个结点,由斐波那契数列(Fibonacci),可得最少有f(m) = f(m-1) + f(m-2) + 1个结点,其中f(1) = 1 、f(2) = 2、f(3) = 4。
例如,具有5层结点的平衡二叉树的结点个数至少为f(5) = f(5-1) + f(5-2) + 1= f(4) + f(3) + 1=[f(3) + f(2) + 1]+[f(2) + f(1) + 1]+1=4+2+1+2+1+1+1=12个结点。
二、平衡因子
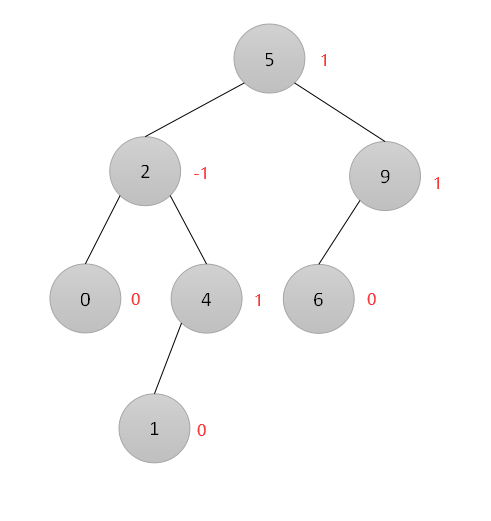
二叉树中左子树的深度减去其右子树深度,称为该结点的平衡因子,平衡二叉树中结点的平衡因子只可能为1、-1或0三种,其中叶子结点的平衡因子均为0,例如下面这个二叉树为平衡二叉树:
叶子结点0、1、6的平衡因子均为0,
结点4的左子树深度为1,右子树深度为0,所以平衡因子为1-0=1,
结点9的左子树深度为1,右子树深度为0,所以平衡因子为1-0=1,
结点2的左子树深度为1,右子树深度为2,所以平衡因子为1-2=-1,
结点5的左子树深度为3,右子树深度为2,所以平衡因子为3-2=1。
而,下图这个二叉树为非平衡二叉树:
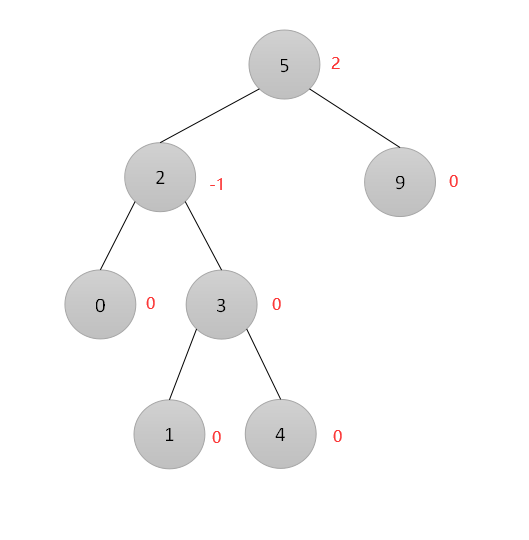
叶子结点0、1、4、9的平衡因子均为0,
结点3的左子树深度为1,右子树深度为1,所以平衡因子为1-1=0,
结点2的左子树深度为1,右子树深度为2,所以平衡因子为1-2=-1,
结点5的左子树深度为3,右子树深度为1,所以平衡因子为3-1=2,不满足平衡二叉树的要求。
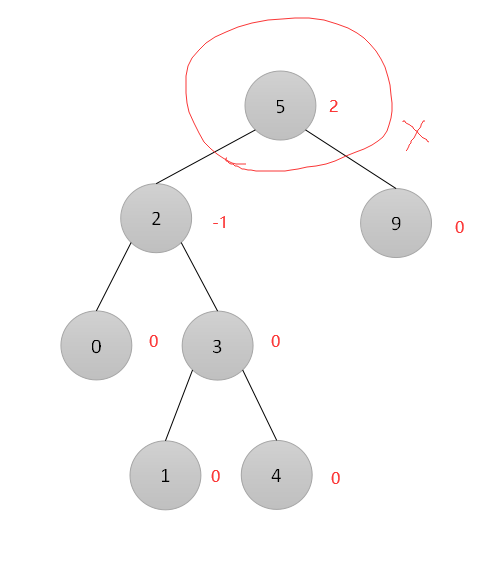
三、平衡二叉树的插入和构造
平衡二叉树的插入操作性质与二叉排序树一样,也是要在保证一定条件下进行插入操作,若导致不满足条件则需要进行调整。若平衡二叉树中插入一个元素时导致发生了不平衡,则需要调整元素的位置关系,使其达到平衡,调整遵循的原则是每次调整的对象都是最小不平衡子树,即离插入结点最近的其平衡因子的绝对值大于1的结点作为根的子树。
插入新结点导致不平衡的情况有以下四种:
| 类别 | 操作 |
|---|---|
| LL型旋转(右单旋转) | 在结点的左子树的左子树插入新结点导致失衡 |
| LR型旋转(先左后右旋转) | 在结点的左子树的右子树插入新结点导致失衡 |
| RR型旋转(左单旋转) | 在结点的右子树的右子树插入新结点导致失衡 |
| RL型旋转(先右后左旋转) | 在结点的右子树的左子树插入新结点导致失衡 |
(一)LL型旋转
若在结点的左子树的左子树插入新结点导致平衡二叉树失衡,则进行LL型旋转,即右单旋转。【向右顺时针旋转】

插入新结点6后导致平衡二叉树失衡,插入位置是结点9的左子树的左子树处,所以进行LL型旋转,如下:
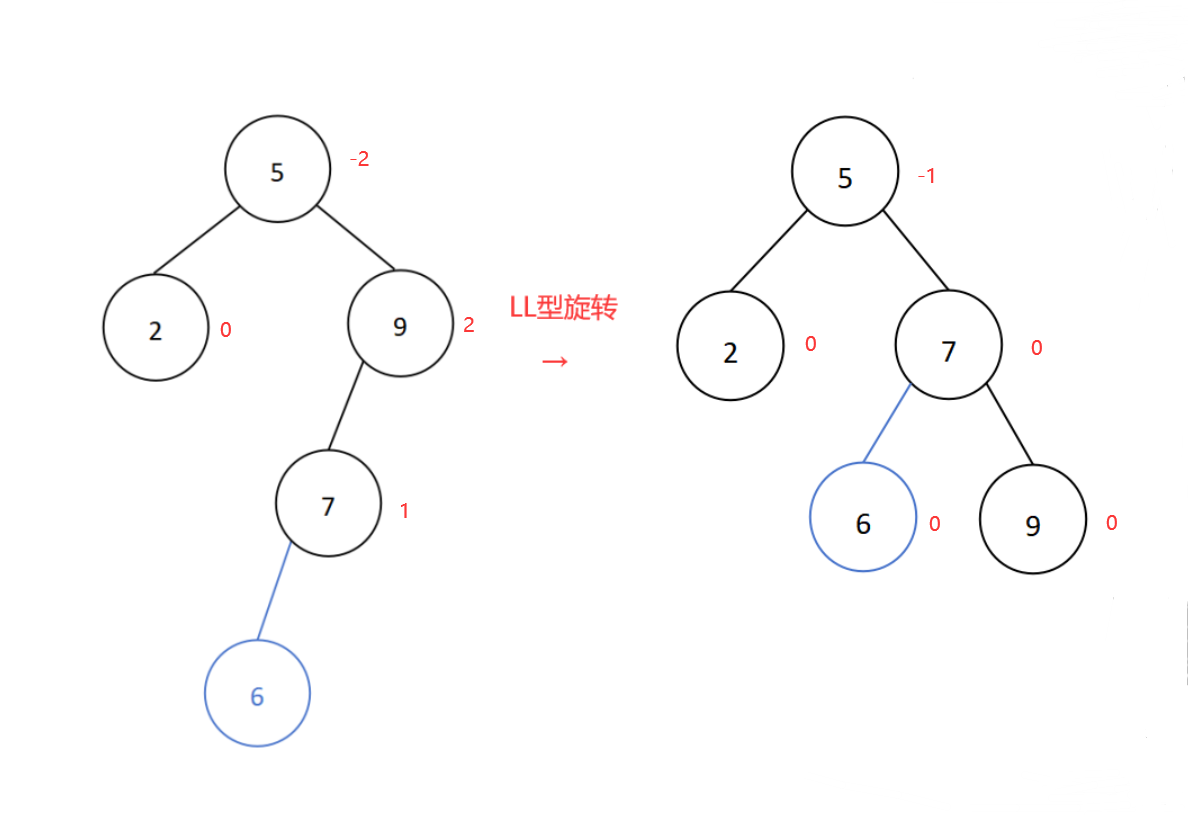
调整后的二叉树即为平衡二叉树。
(二)LR型旋转
若在结点的左子树的右子树插入新结点导致平衡二叉树失衡,则进行LR型旋转。【先左旋转后右旋转】
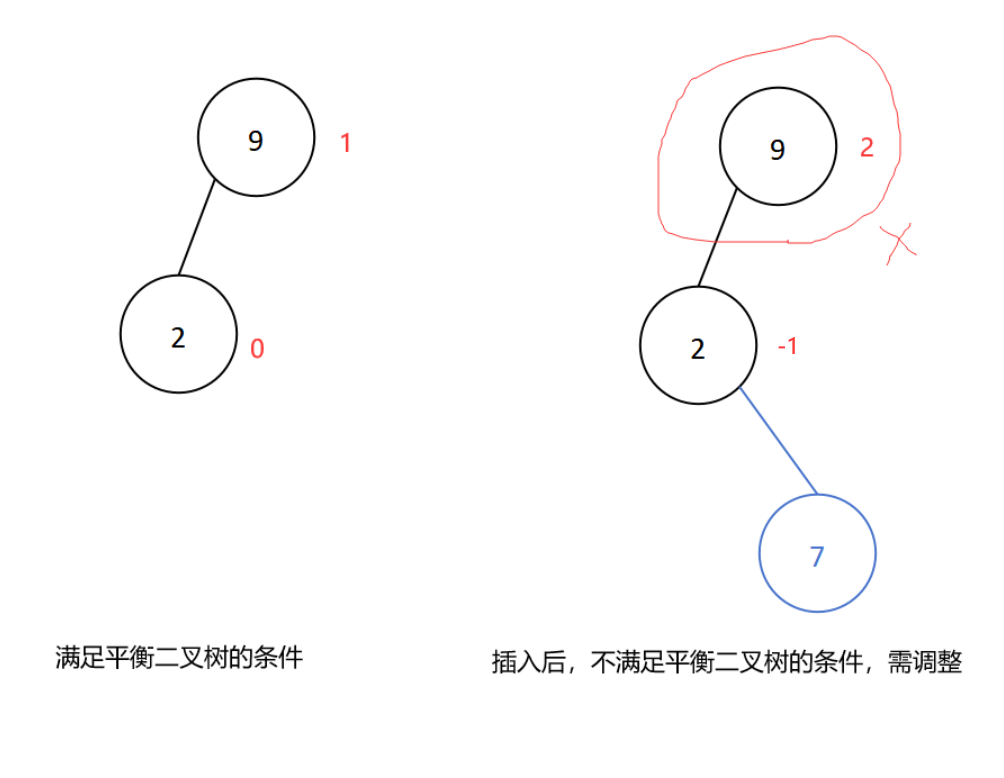
插入新结点7后导致平衡二叉树失衡,插入位置是结点9的左子树的右子树处,所以进行LR型旋转,如下:
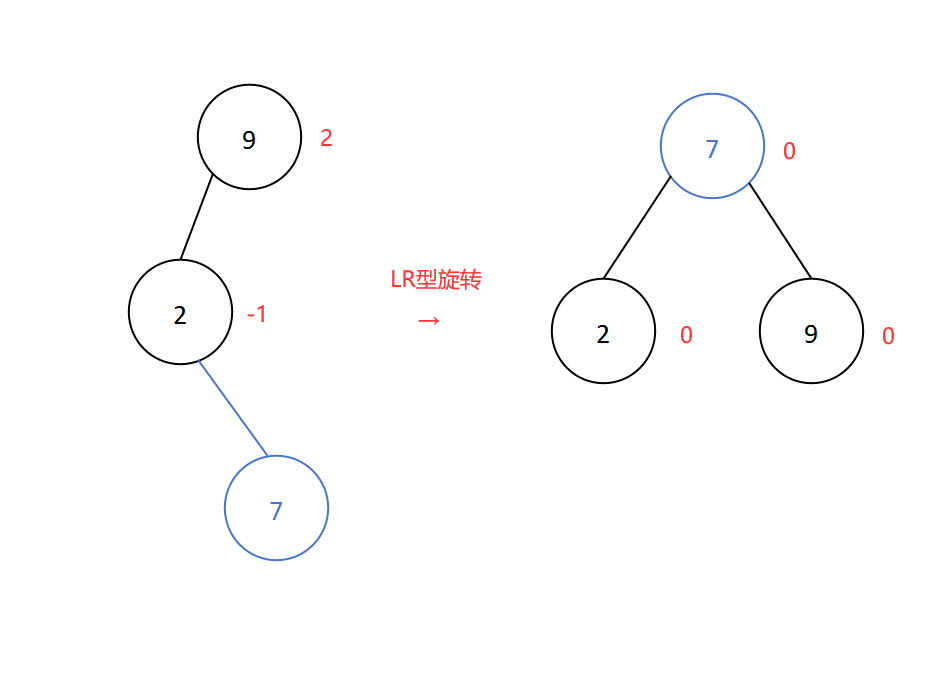
调整后的二叉树即为平衡二叉树。
(三)RR型旋转
若在结点的右子树的右子树插入新结点导致平衡二叉树失衡,则进行RR型旋转,即左单旋转。【向左逆时针旋转】
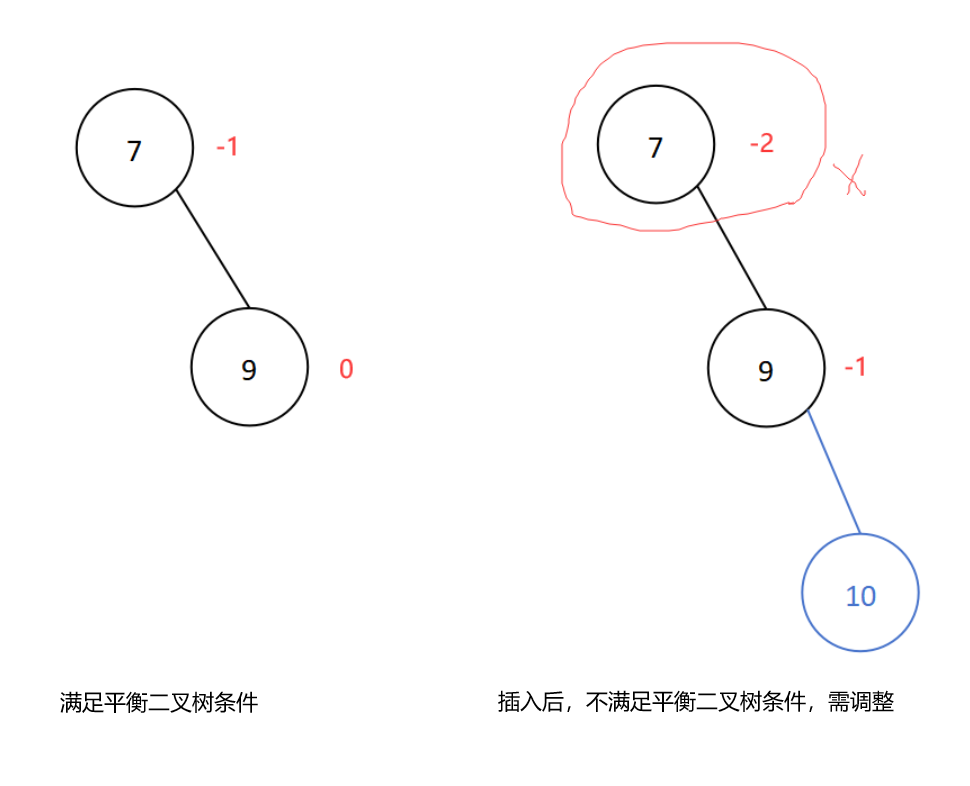
插入新结点10后导致平衡二叉树失衡,插入位置是结点7的右子树的右子树处,所以进行RR型旋转,如下:
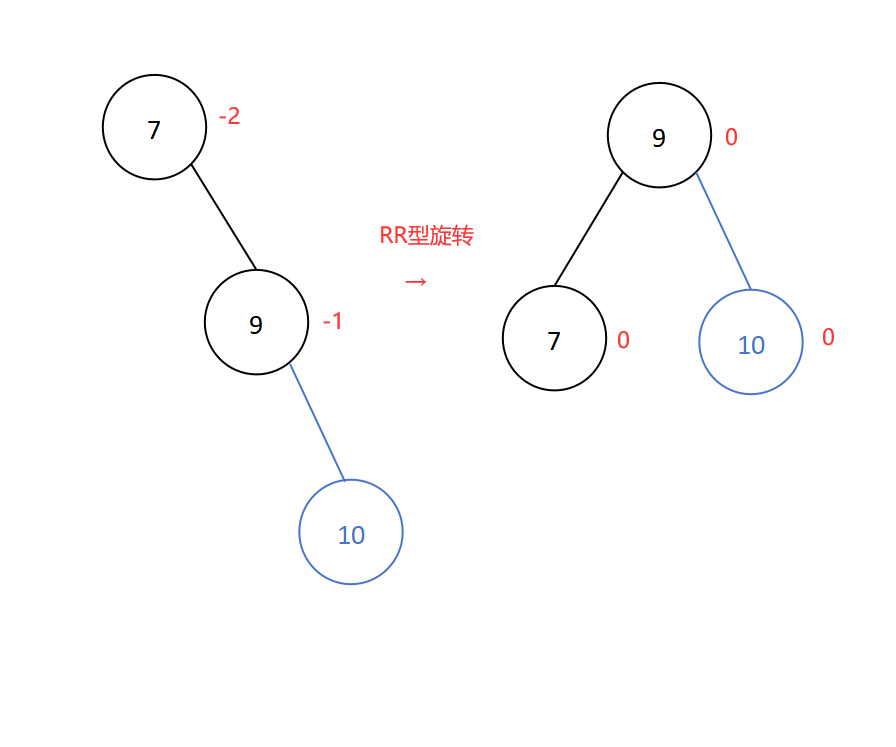
调整后的二叉树即为平衡二叉树。
(四)RL型旋转
若在结点的右子树的左子树插入新结点导致平衡二叉树失衡,则进行RL型旋转。【先右旋转后左旋转】
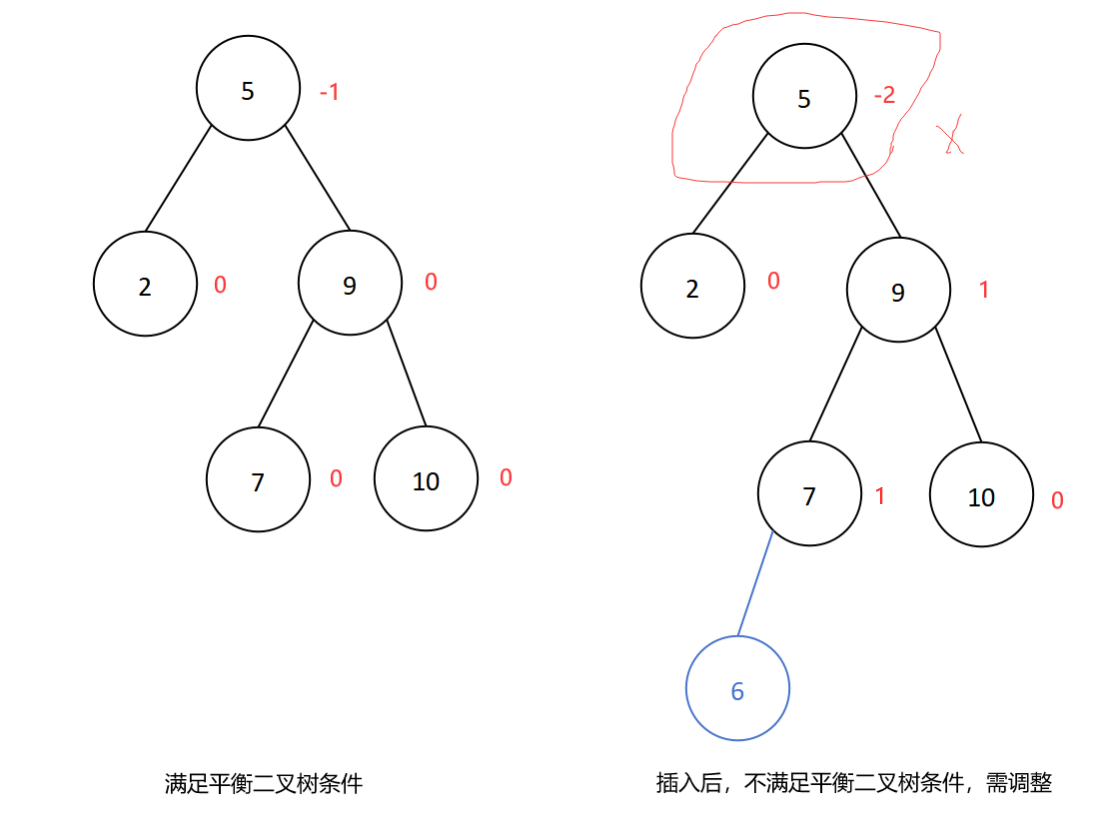
插入新结点6后导致平衡二叉树失衡,插入位置是结点5的右子树的左子树处,所以进行RL型旋转,如下:
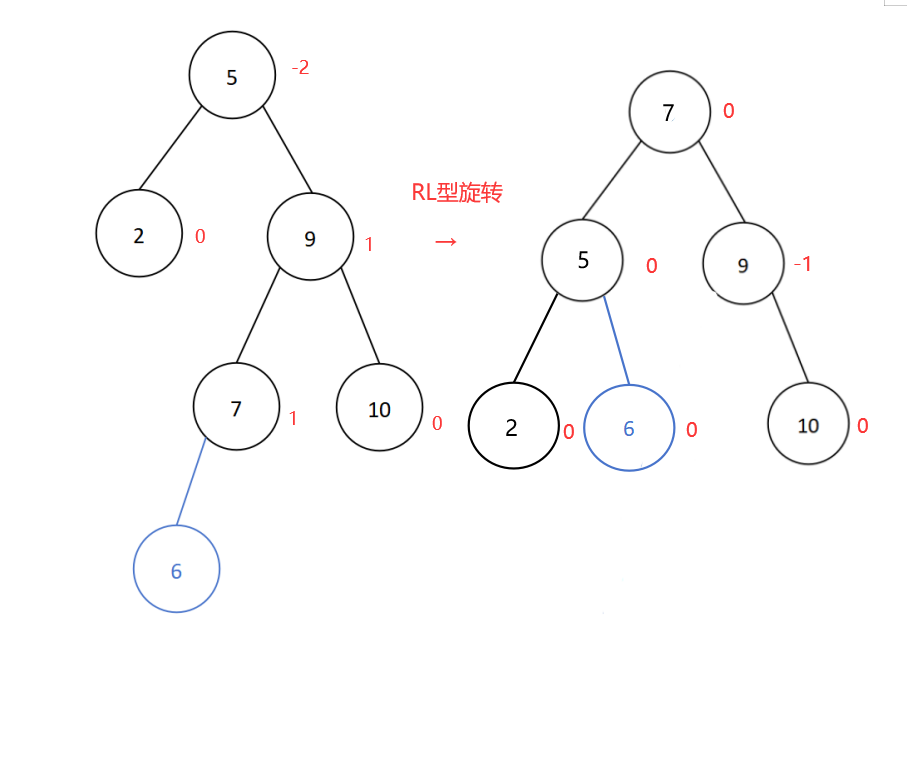
调整后的二叉树即为平衡二叉树。
四、平衡二叉树的删除
(一)叶子结点
平衡二叉树中,若要删除的结点只有叶子结点,则可直接将其删除,不影响平衡二叉树。
例如,删除平衡二叉树中的结点9,由于该结点是叶子结点,所以直接删除,如下:

(二)只有左/右子树,没有右/左子树
平衡二叉树中,若要删除的结点只有左/右子树,没有右/左子树,此时将该结点删除,后面的子结点接上即可,从而不影响平衡二叉树。
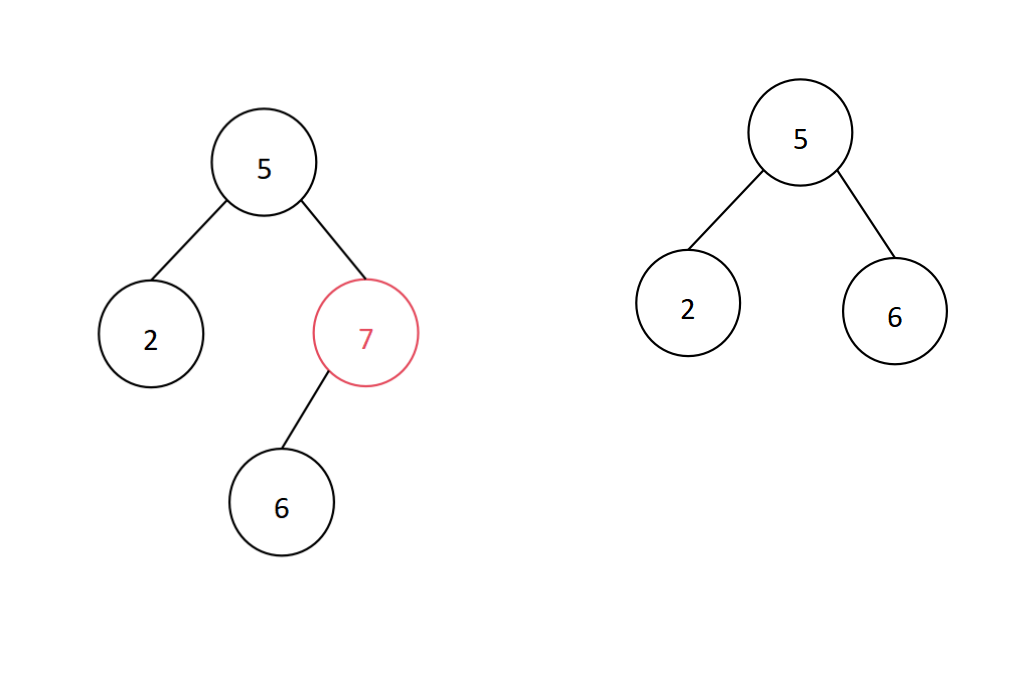
(三)既有左子树,又有右子树
平衡二叉树中,若要删除的结点既有左子树,又有右子树,此时可沿着左(右)子树的右(左)指针,一直走到右(左)子树的最右(左)边的一个结点,用该结点与要删除的结点代替【找到交换的结点】,然后,可以将其转换为(一)、(二)中的情况,若替代后,该结点为叶子结点则按照(一)进行删除,若非叶子结点则按照(二)进行删除。
例如,删除平衡二叉树中结点11,首先找到要交换的结点,即结点9,所以结点11与结点9进行交换,如下:
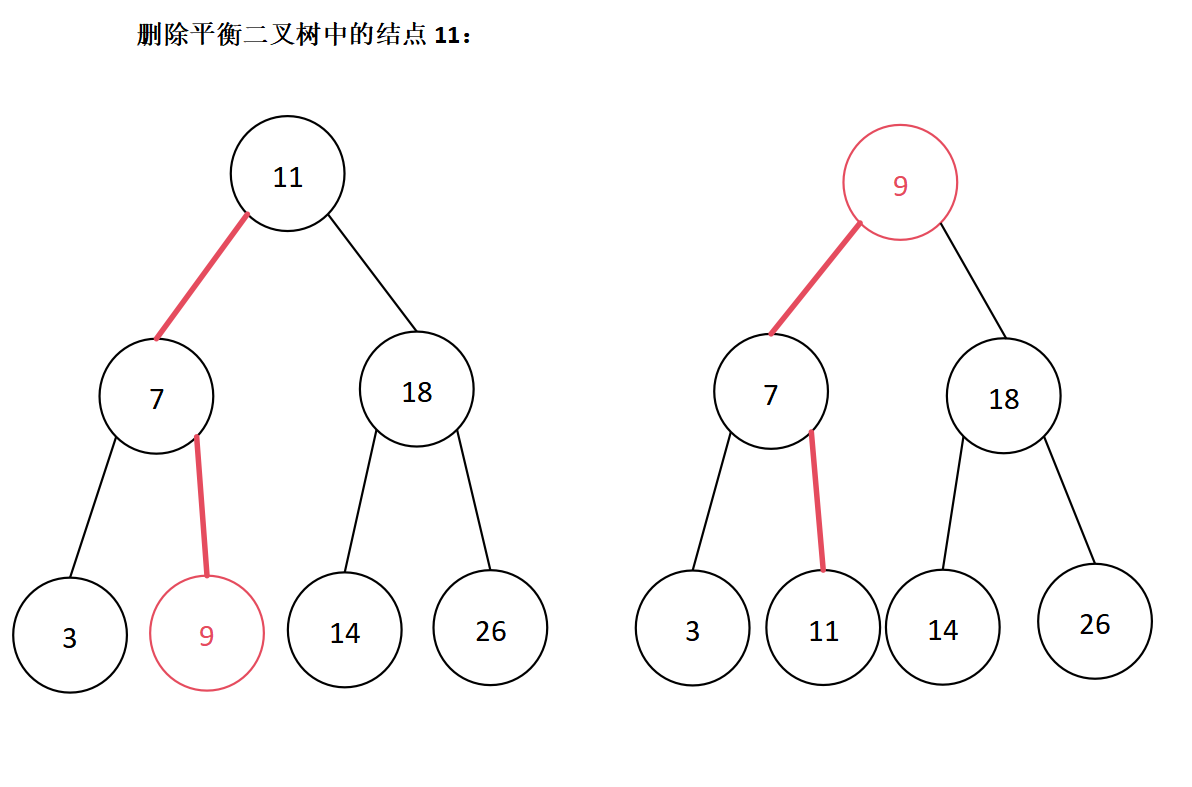
然后,由于此时结点11是叶子结点,此时转换为第一种情况,所以可直接删除,如下:
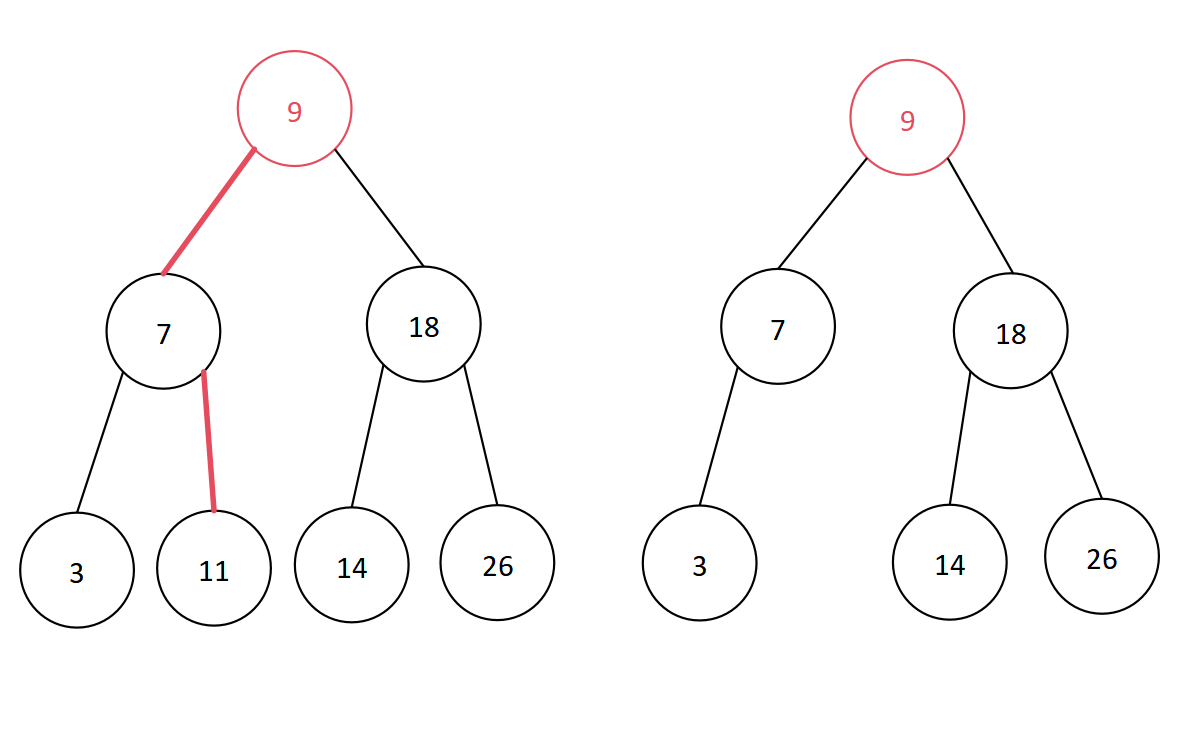
五、平衡二叉树的查找和平均查找长度
平衡二叉树的查找与二叉排序树一样,含有n个结点的平衡二叉树的最大深度为h=⌈log2(n+1)⌉,所以其平均查找长度为O(log2n),另外平衡二叉树的最小深度为h=⌈log2(n+1)⌉。
相关文章:

数据结构学习笔记——查找算法中的树形查找(平衡二叉树)
目录 一、平衡二叉树的定义二、平衡因子三、平衡二叉树的插入和构造(一)LL型旋转(二)LR型旋转(三)RR型旋转(四)RL型旋转 四、平衡二叉树的删除(一)叶子结点&a…...

P1830 轰炸III
题目背景 一个大小为 ��nm 的城市遭到了 �x 次轰炸,每次都炸了一个每条边都与边界平行的矩形。 题目描述 在轰炸后,有 �y 个关键点,指挥官想知道,它们有没有受到过轰炸,如…...

大语言模型LLM知多少?
你知道哪些流行的大语言模型?你都体验过哪写? GPT-4,Llamma2, T5, BERT 还是 BART? 1.GPT-4 1.1.GPT-4 模型介绍 GPT-4(Generative Pre-trained Transformer 4)是由OpenAI开发的一种大型语言模型。GPT-4是前作GPT系列模型的进一步改进,旨在提高语言理解和生成的能力,…...

Redis命令行使用Lua脚本
Redis命令行使用Lua脚本 Lua脚本在Redis中的使用非常有用,它允许你在Redis服务器上执行自定义脚本,可以用于复杂的数据处理、原子性操作和执行多个Redis命令。以下是Lua脚本在Redis中的基本使用详细讲解: 运行Lua脚本: 在Redis中…...

HTML详细基础(三)表单控件
本帖介绍web开发中非常核心的标签——表格标签。 在日常我们使用到的各种需要输入用户信息的场景——如下图,均是通过表格标签table创造出来的: 目录 一.表格标签 二.表格属性 三.合并单元格 四.无序列表 五.有序列表 六.自定义标签 七.表单域 …...
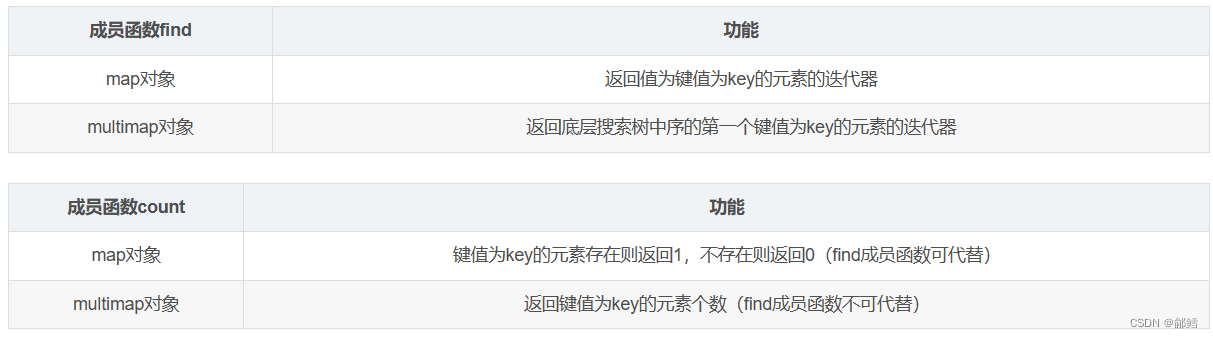
map和set的具体用法 【C++】
文章目录 关联式容器键值对setset的定义方式set的使用 multisetmapmap的定义方式insertfinderase[]运算符重载map的迭代器遍历 multimap 关联式容器 关联式容器里面存储的是<key, value>结构的键值对,在数据检索时比序列式容器效率更高。比如:set…...
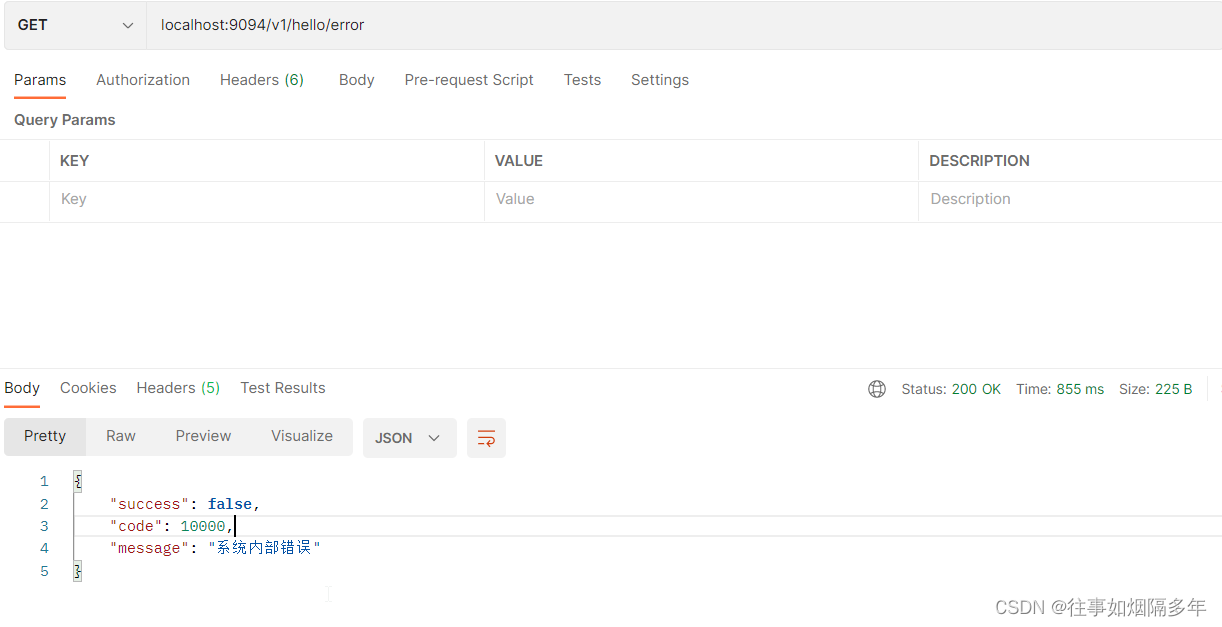
聚合统一,SpringBoot实现全局响应和全局异常处理
目录 前言 全局响应 数据规范 状态码(错误码) 全局响应类 使用 优化 全局异常处理 为什么需要全局异常处理 业务异常类 全局捕获 使用 优化 总结 前言 在悦享校园1.0版本中的数据返回采用了以Map对象返回的方式,虽然较为便捷但也带来一些问题。一是在…...
【C/C++笔试练习】——数组名和数组名、switch循环语句、数据在计算机中的存储顺序、字符串中找出连续最长的数字串、数组中出现次数超过一半的数字
文章目录 C/C笔试练习1.数组名和&数组名(1)数组名和&数组名的差异(2)理解数组名和指针偏移(3)理解数组名代表的含义(4)理解数组名代表的含义 2.switch循环语句(6…...
力扣每日一题(+日常水题|树型dp)
740. 删除并获得点数 - 力扣(LeetCode) 简单分析一下: 每一个数字其实只有2个状态选 or 不 可得预处理每一个数初始状态(不选为0,选为所有x的个数 * x)累加即可 for(auto &x : nums)dp[x][1] x;每选一个树 i 删去 i 1 和 i - 1 故我们可以将 i…...

使用perming加速训练可预测的模型
监督学习模型的训练流程 perming是一个主要在支持CUDA加速的Windows操作系统上架构的机器学习算法,基于感知机模型来解决分布在欧式空间中线性不可分数据集的解决方案,是基于PyTorch中预定义的可调用函数,设计的一个面向大规模结构化数据集的…...

【数据库】存储引擎InnoDB、MyISAM、关系型数据库和非关系型数据库、如何执行一条SQL等重点知识汇总
目录 存储引擎InnoDB、MyISAM的适用场景 关系型和非关系型数据库的区别 MySQL如何执行一条SQL的 存储引擎InnoDB、MyISAM的适用场景 InnoDB 是 MySQL 默认的事务型存储引擎,只有在需要它不支持的特性时,才考虑使用其它存储引擎。实现了四个标准的隔…...

车道线分割检测
利用opencv,使用边缘检测、全局变化梯度阈值过滤、算子角度过滤、HLS阈值过滤的方法进行车道线分割检测,综合多种阈值过滤进行检测提高检测精度。 1.利用cv2.Sobel()计算图像梯度(边缘检测) import cv2 import numpy as np import matplotlib.pyplot a…...

树莓集团又一力作,打造天府蜂巢成都直播产业园样板工程
树莓集团再次推出惊艳之作,以打造成都天府蜂巢直播产业园为目标。该基地将充分展现成都直播产业园的巨大潜力与无限魅力,成为一个真正的产业园样板工程。 强强联手 打造未来 成都天府蜂巢直播产业园位于成都科学城兴隆湖高新技术服务产业园内࿰…...

ubuntu 软件包管理之二制作升级包
Deb 包(Debian 软件包)是一种用于在 Debian 及其衍生发行版(例如 Ubuntu)中分发和安装软件的标准包装格式。它们构成了 Debian Linux 发行版中的软件包管理系统的核心组成部分,旨在简化软件的分发、安装、更新和卸载流程。在本篇文章中,我们将深入探讨以下内容: Deb 包基…...
)
TCP/IP网络江湖——数据链路层的防御招式(数据链路层下篇:数据链路层的安全问题)
目录 引言 一、 数据链路层的隐私与保密 二、数据链路层的安全协议与加密...

ios项目安装hermes-engine太慢问题
问题说明 ios工程,在使用"pod install"安装依赖的时候,由于超时总是报错 $ pod install ... Installing hermes-engine (0.71.11)[!] Error installing hermes-engine [!] /usr/bin/curl -f -L -o /var/folders/4c/slcchpy55s53ysmz_1_q_gzw…...
构建个人云存储:本地电脑搭建SFTP服务器,开启公网访问,轻松共享与管理个人文件!
本地电脑搭建SFTP服务器,并实现公网访问 文章目录 本地电脑搭建SFTP服务器,并实现公网访问1. 搭建SFTP服务器1.1 下载 freesshd 服务器软件1.3 启动SFTP服务1.4 添加用户1.5 保存所有配置 2. 安装SFTP客户端FileZilla测试2.1 配置一个本地SFTP站点2.2 内…...

springboot 下载文件为excel数据,中文自定义单元格宽度
/**2 * Description:表格自适应宽度(中文支持)3 * Author: 4 * param sheet sheet5 * param columnLength 列数6 */7 private static void setSizeColumn(HSSFSheet sheet, int columnLength) {8 for (int columnNum 0; columnNum < …...

机器学习 面试/笔试题
1. 生成模型 VS 判别模型 生成模型: 由数据学得联合概率分布函数 P ( X , Y ) P(X,Y) P(X,Y),求出条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的预测模型。 朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机…...

某企查ymg_ssr列表详情
js篇— 今天来看下某企查的列表详情–侵删 header发现这个参数 先断点一下 然后上一步 就到了这个地方 就开始扣一下这个js 三大段,先不解混淆了, 给a粘贴出来 ,去掉自执行 给结果稍微改一下 缺windows,开始补环境 直接上…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
