趣味三角——第12章——tanx
第12章节 tanx
In his very numerous memoires, and especially in his
great work, Introductio in analysin infinitorum (1748),
Euler displayed the most wonderful skill in obtaining a
rich harvest of results of great interest. . . . Hardly any
other work in the history of Mathematical Science gives
to the reader so strong an impression of the genius of the
author as the Introductio.
(欧拉在他数量众多的回忆录中,尤其是在他的伟大著作<<Introductio in analysin infinitorum>>(无穷小分析引论)(1748 年)中,展示了获得大量有趣结果的绝妙技巧……在数学科学史上,几乎没有任何其他著作能给给予读者能像引论一样,留下如此强烈的作者的天才印象。)
——E. W. Hobson, “Squaring the Circle”: A History of the Problem (“化圆为方”:一个历史问题)(1913)
在我们在初级函数中遇到的众多函数中,也许最著名的函数要数正切函数(tangent)。基本事实是众所周知的:f(x) = tan x 在x = nπ(n = ±0, ±1,±2,...)处其值为0,在x = (2n + 1)π/2 (n = ±0, ±1,±2,...)处无限不连续,以及具有周期性(对于一个函数f(x),假如P是使得关系f(x + P ) = f(x)对于函数定义域上的所有x都成立的最小值,则就称函数f(x)为周期函数,其周期为P),周期为π。最后一个事实非常值得注意:函数 sin x 和 cos x 具有共同的周期 2π,但它们的比率tan x将周期减少为π。当谈到周期性时,函数代数的一般规则可能无效:两个函数 f 和 g 有一个共同的周期 P 并不意味着 f + g 或 fg 也有相同的周期。[1]
正如我们在第 2 章中看到的,正切函数起源于古代的“影子计算(shadow reckoning)”。 在文艺复兴时期,它与刚刚兴起的(fledging)透视艺术(透视画法)(art of perspective)相关,虽然当时并没有称之为“切线”,但其确实又复活了(resurrected)。一个物体随着远离观察者而逐渐变小是一种常见的体验。 从地面观看高层建筑时,效果尤为明显:随着视角升高,垂直等间距的特征(例如建筑物的地板)似乎逐渐缩短;反之,等量的仰角增量与结构相距越来越远的点相交。著名的纽伦堡艺术家Albrecht Dürer(1471-1528年)是透视法的创始人之一,他的一项研究清楚地表明了这种效果(图 75)。[2]
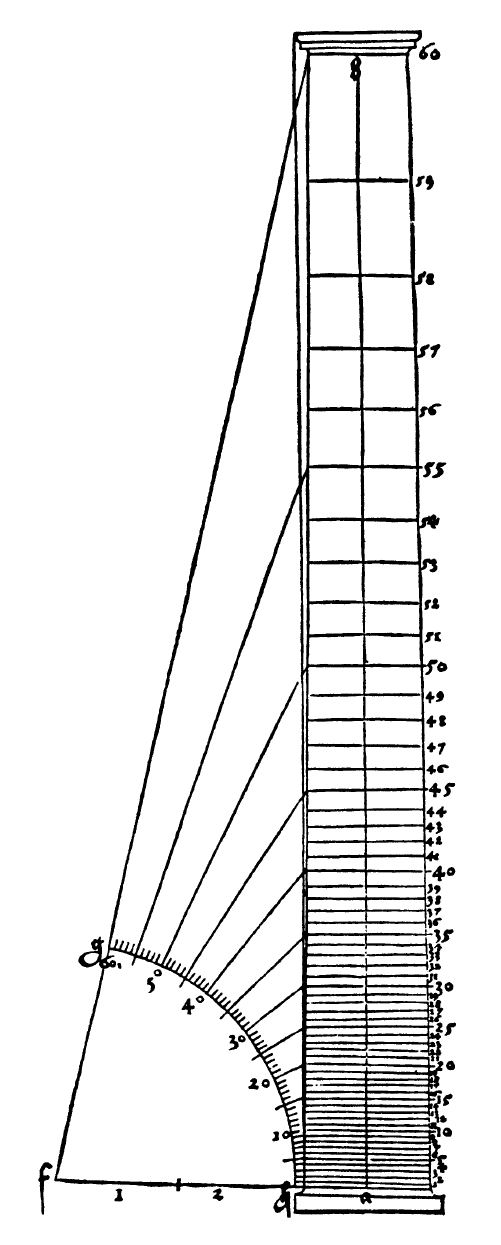
--------------------------图75 Albrecht Dürer的一项研究------------------------
当仰角接近90度并且高度似乎无限制地增加时,Dürer和他的同时代人对这种现象的极端情况特别感兴趣。更有趣的是平面中平行线的行为:当它们远离观察者时,它们似乎越来越近,最终汇聚在地平线上的一个点,称为“消失点(vanishing point)”。所有这些特征都可以追溯到接近 90°的 tan x 的行为。今天,当然,我们说当 x 接近90°时tan x趋于无穷大,而在90°时它是不确定的;但这种微妙之处不为前人所知,直到最近,人们仍然可以在许多三角学教科书中找到“tan 90°= ∞”这一说法。
但是让我们回到世俗的事情上。大约在1580年,Viète 提出了一个美丽的定理,遗憾的是,该定理几乎从今天的教科书中消失了:切线定律(the Law of Tangents)。它说的是,在任何三角形中,
。---------------------------------------------------------------(1)
这个定理是从正弦定理(a/sin(α)= b/sin(β)= c/sin(γ))以及恒等式
推出,但是在Viète时期,它被看作一个独立的定理。[3] 当已知三角形的两条边及其夹角时(SAS——边角边的情况),可用以求三角形。通常,人们喜欢用余弦定理(
) 来求得另一条边,然后使用正弦定理来求得一个角或其它的角。然而,由于余弦定律涉及加法和减法,它并不适合对数计算——实际上它只是在手持计算器问世之前求解三角形(或大多数其他计算)的唯一方法。使用切线法可以避免这一困难:因为已知一个角,比如说γ,你可以求得(α + β)/2,然后在方程(1)以及正切表的帮助下求得(α - β)/2;从这两个结果出发,就可以求得α和β,最后,利用正弦定理就可以求得另外两条未知的边。当然,有了计算器就没有必要了,这或许可以解释为什么切线定律失去了大部分吸引力。尽管如此,它优雅的对称形式应该是一个足够好的理由让它从遗忘中复活,如果不是作为一个定理,那么至少作为一个练习还是有必要的。对于那些喜欢数学“错误(misteakes)”的人——歪打正着(例如1
6/64 = 1/4)——正切法则为此提供了充裕的(ample)机会: 以方程(1)的右侧开始,“消除”1/2和“tan”,用对应的拉丁字母替换掉希腊字母,则你会得到左侧的部分。[4]
其他涉及 tan x 的公式同样优雅;例如,如果α, β,和γ是任意三角形的三个角,我们有
tan α + tan β + tan γ = tan α .tan β .tan γ ----------------------------------(1)
这个公式可以通过将角度关系写成γ = 180°- (α + β)以及对正切使用加法公式来证明。这个公式的著名之处不仅在于完美的对称性,而且还因为其导致了一个出人意料的结果。来自代数的一个著名的定理说的是,假如 是任意正整数, 那么它们的算术平均值永远不会小于它们的几何平均值;即,
此外,当且仅当 时,这两个均值相等。我们假设我们的三角形是锐角三角形(acute triangle),因此,所有三个角都具有正值的正切值,则定理说的是
。
但是鉴于等式(2),这种不等式变为
不等式两边取立方得到
。
因此,在任意锐角三角形中,三个角的正切之积(以及之和)不小于 当且仅当角α = β = γ = 60°时,即三角形为等边三角形时,不等式取得最小值。
如果三角形是钝角(obtuse),则三个角之一有负切线,在这种情况下定理不适用;然而,由于钝角只能在90°到180°之间变化,因此它的切线范围在区间(-∞,0)内;而其他两条切线保持正值且有限。因此,三个正切的乘积可以取任何负值。
结论是,在任意锐角三角形中,我们有 (当且仅当三角形为等边三角形时取得等号),以及在任意钝角三角形中,我们有
。
角度的倍数的正切为我们提供了有趣公式的另一个来源。在第8章中我们获得了公式
我们可以令α/2 = β,以及n + 1 = m ,改写一下等式,使其略为更加有用;则有
。
但即使是这种形式,该公式的用处也很有限,因为它用其他角度的正弦和余弦表示一个角度的倍数的正切。如果我们能用α的正切(并且单独地,而不是它的倍数)来表示tan nα,那将是可取的(desirable)。幸运的是,这是可以做到的。
我们以正切的加法公式为出发点,
。
从这个基本公式出发,我们得到
等等。几步之后,一种模式开始出现:我们发现其系数与 展开式中x幂项的系数相同——我们熟悉的二项式系数(binomial coefficients)——除了它们以锯齿形模式(zigzag pattern)在分子(numerator)和分母(denominator)之间交替(从分母中的第一项开始)并且它们的符号成对交替。[5] 图76取自19世纪初的三角学教科书,显示了tan 7α以内的模式。考虑到符号,我们可以将系数排列在“帕斯卡正切三角形(Pascal tangent triangle)”中:
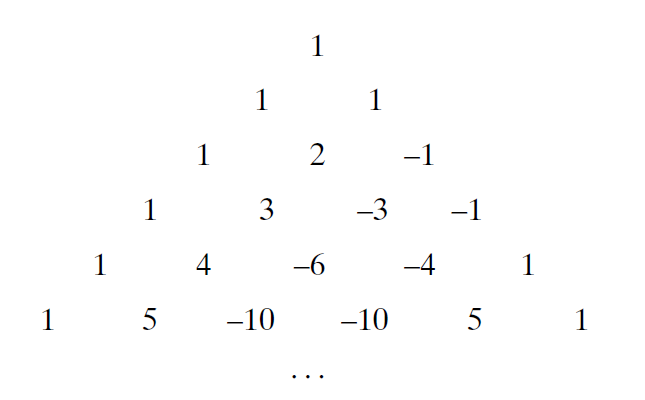
(顶部元素为 1,因为 tan 0 = 0 = 0/1)。我们注意到前两条对角线(从左到右计数)中的所有条目都是正数,接下来两行的所有条目都是负数,依此类推。

--------图76 tan(nα) 的 tan(α) 幂的展开。来自 19 世纪初的三角学书籍。---------
公式中出现的二项式系数似乎与的展开无关,这是De Moivre定理的结果(参见第 83 页),
其中, 。如果我们根据二项式定理将式(3)的左边展开,使右边的实部和虚部相等,我们就得到cos(nα)和sin(nα)按
(其中,k = 0, 1 , 2 , ... , n)表示的表达式;据此,很容易推出tan(nα)的公式;
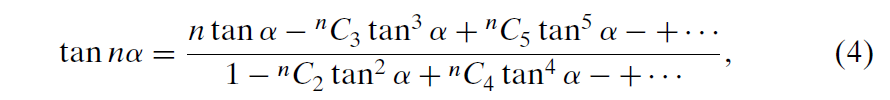
其中,符号
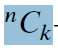
也可以使用来表示——表示
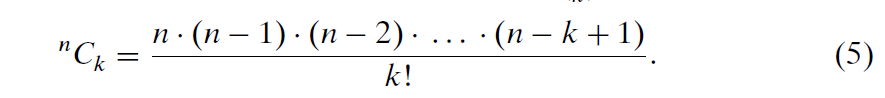
例如,
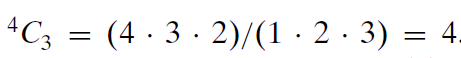
注意,公式(5)右侧的表达式也等于n!/[k!.(n - k)!],因此,我们有
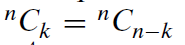
(正如例子中给出来的那样,
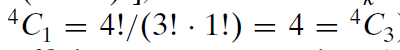
)。由于这个原因,二项式系数是对称的——无论你以x的幂按升序或降序展开它都是一样的。
因为 对于正整数数n包括(n + 1)项,出现在等式(4)中的分子和分母的级数是有限项之和,但是,所有6个三角函数也可以通过无限(infinite)表达式来表示,特别是幂级数(power series)和无限积。sin x和cos x的幂级数是
和
。
牛顿早已知道这些级数,但伟大的瑞士数学家Leonhard Euler(1707-1783年)使用它们得出了大量新结果。Euler将幂级数视为“无限多项式(infinite polynomials)”,它们遵循与普通有限多项式相同的代数规则。因此,他认为,正如n次多项式可以写成形如(其中,
为多项式的根或者为0 [6])的n个因子(不必相异)的乘积一样,函数sin x也可以写成无限积的形式
。------------------------------------------(6)
在这里,每一个二次项都是两个线性因子(1-x/(nπ))和(1+ x/(nπ))的乘积,由sin x的零点产生,xn
![]() =±nπ ,而单个因子x由x = 0 的零点产生。[7] 如果我们代入x = π/2,方程式 (6) 的一个令人惊讶的结果是:
=±nπ ,而单个因子x由x = 0 的零点产生。[7] 如果我们代入x = π/2,方程式 (6) 的一个令人惊讶的结果是:
1 = (π/2).(1-1/4).(1-1/16).(1-1/36)...。
简化每一项并求解π/2 ,我们得到无限项
。--------------------------------------------------------------------------------------------(7)
这个著名的公式以John Wallis的名字命名(见第51页), 他在1655年通过大胆的插值(interpolation)过程发现了它。[8]
cos x 的无限积是
其中,是cos x的零值点(此外,在这儿,每个二项式因子都是两个线性因子的乘积)。假如我们现在用等式(8)除以等式(6),我们就得到针对tan x的解析表达式:
。----------------------(9)
然而,这种表述相当麻烦。为了简化它,让我们使用一种来自积分学中的熟悉技术——将比率函数分解为“部分分数(partial fractions)”。 我们将等式(9)的右边表示为分数的无穷和,每个分数的分母等于等式(9)的分母中的一个线性因子:
。---------(10)
为了求得分解式的系数,让我们“清零分数”:我们将等式(10)的两边乘以所有分母的乘积(即乘以cos x),并将结果等同于等式(9)的分子(即对sin x):
x(1- x/π)(1+ x/π)(1- x/(2π))(1+ x/(2π))...
=A1![]() (1+ 2x/π)(1- 2 x/(3π))(1+ 2 x/(3π))...
(1+ 2x/π)(1- 2 x/(3π))(1+ 2 x/(3π))...
+ B1![]() (1- 2x/π)(1 - 2 x/(3π))(1 + 2 x/(3π))...
(1- 2x/π)(1 - 2 x/(3π))(1 + 2 x/(3π))...
+ ... -----------------------------------------------------------------(11)
请注意,在等式(11)右侧的每一项中,恰好缺少一个因子——等式(10)中相应系数的分母(就像求普通公分母时一样)。
现在,等式(11)在x中是查恒等式——它适用于我们选择置入其中的任何x值。为了求得 ,我们取
= π/2 ;这将“消灭(annihilate)”除第一项以外的所有项,得出
(π/2).(1/2).(3/2).(3/4).(5/4)....
= .2.(2/3).(4/3).(4/5).(6/5)....
对 解方程,我们得到
。
但是括号内的表达式正好是Wallis乘积的倒数(reciprocal),即,,因此,我们有
。
为了求得 ,在等式(11)中,我们除了令 x = -π/2之外,我们遵循同样的流程;求出
= -2/π = 。其它的系数可按类似的方式求得;[9] 我们求得
,
,以通式表达为
。
将这些系数放回到等式(10)中并将各项成对组合,我们得到大奖(grand prize),将tan x 分解为部分分数:
。-------------------------(12)
这个著名的公式直接表明,tan x在 x = ±π/2, ±3π/2,...处无定义;显然,这些正是tan x的垂直渐近线。
既然我们在建立方程式(12)上花费了如此多的精力,那么让我们从中获得一些好处。 因为等式对所有除了(2n + 1)πx/2(n = 0,±1,±2,...)之外的都成立x值都成立,现在,让我们代入一些特殊值。我们以x = π/4 开始:
。
括号中的第一项格式为
因此,我们有
1 = (π/4)[1 – 1/3 + 1/5 - 1/7 + - ...] ,
据此,我们得到
。---------------------------------------(13)
这个著名的公式由苏格兰数学家James Gregory(1638-1675年)于1671年发现,他从反正切的幂级数推导出来。
在这个反正切等式中,代入x = 1,得到等式(13)。1674年Leibniz独立发现了同一个公式,所以这个公式也常以他的名字命名。[10] 这是新发明的微积分的第一个成果之一,它让Leibniz非常高兴。
Gregory-Leibniz级数(也是Wallis的乘积)的非凡之处在提示了于π和整数之间出乎意料的联系。然而,由于其收敛速度非常慢,从计算的角度来看,该级数几乎没有用处:它需要628项才能将π逼近到小数点后两位——同样使用穷尽法,其精度远低于阿基米德(Archimedes)在两千多年前使用该方法获得的精度。尽管如此,Gregory-Leibniz级数标志着数学史上的一个里程碑,它是未来几年将要发现的众多涉及π的无限级数中的第一个。
下一步,我们用x = 1 代入等式(12),我们得到:
。
消掉(8/π)并将负项移到等式的左侧,我们得到
1/5 + 1/21 + 1/45 + ... = 1/3 。
或许有些令人失望的是,我们得到了一个不涉及π的级数,但是当我们尝试将 x = 0代入等式(12)时,我们的兴奋又回来了。起初我们只是得到不定方程 0 = 0,但我们可以通过将等式两边除以 x 然后让 x 趋近于零来解决这个困难。在左边我们得到
。
因此,等式(12)成了
或
。---------------------------------(14)
最后一个公式与Gregory-Leibniz级数一样引人注目,但我们可以从中推导出一个更有趣的结果。我们将再次以一种非严格的方式来做这件事,本着(in the spirit of)Euler大胆探索无限级数世界的精神(更严格的证明将在第 15 章中给出)。 我们的任务是找出所有正整数(偶数和奇数)的平方的倒数之和;让我们用 S 表示这个和:[12]
据此,我们得到 ,最后
。---------------------------------(15)
等式(15)是所有数学中最著名的公式之一;它是Euler在1734年灵机一动中发现的,它挑战了所有现代严格标准。它的发现解决了18世纪的一个重大谜团:一段时间以来,人们就知道级数收敛,但它的总和的值却让当时最伟大的数学家望而却步,其中包括伯努利(Bernoulli)兄弟。[13]
我们考虑Euler发现的另一个无穷级数。 我们从余切的双角公式开始,
。
以 x ≠ (nπ)/2的任意角重复应用到公式,我们得到
=...
。
随着n->∞,趋近于
[14],因此,我们得到
或
。-----------------------(16)
这个鲜为人知的公式是从Euler的想象力中浮现出来的数百个涉及无限过程的公式之一。 在它的背后隐藏着一个惊喜:如果我们代入 ,我们得到
。
用 替换掉左侧的1,并将所有正切换移到等式右侧,等式再除以4,我们得到
。-----------------------(17)
等式(17)在数学中肯定是最美的,但它几乎没有出现在教科书中。此外,右侧的级数收敛得非常快(请注意,系数“和”角度每项按1/2倍递减),因此我们可以使用等式(17)作为一种近似π值的有效方法:它只需要十二项即可取得小数点后6位精度,即百万分之二;再增加四项将使准确度提高到十亿分之一。[15]
我们遵循Euler的精神来处理等式(6)和(9),就好像它们是有限的表达式一样,服从普通代数的规则。Euler生活在一个无忧无虑的数学探索时代,那时对无穷级数的正式操作是一种正常的做法; 收敛和极限问题尚未得到充分理解,因此大体上被忽略了。今天我们知道这些问题对所有无限过程都至关重要,忽视它们会导致错误的结果。[16] 引用一句George F. Simmons在他出色的微积分教科书中的话:“这些大胆的猜测是Euler独特天赋的特征,但我们希望没有学生会认为它们具有严格证明的力量(These daring speculations are characteristic of Euler’s unique genius, but we hope that no student will suppose that they carry the force of rigorous proof)。” [17]
注释和资源来源:
1. 这种情况的一个简单例子是函数f(x) = sinx ,g(x) = 1 – sinx 。其每个函数的周其都是2π,而它们的和 f(x) + g(x) = 1 ,是一个常量,任意实数都可作为其周期。
2. 关于Dürer的数学著作,请参见Julian Lowell Coolidge的<<The Mathematics of Great Amateurs>>(伟大的数学业余爱好者)( 1949 年初版; New York: Dover, 1963年重印)第 5 章,以及Dan Pedoe 的著作<<Geometry and the Liberal Arts>>(几何与人文科学)( New York: St. Martin’s Press,1976年版) 第2章。
3. 这个法则的一个等价形式,其中等式的左侧用(sinα + sinβ)/( sinα + sinβ)替换, Regiomontanus 在1464 年左右就已经知道了,但奇怪的是他并没有在他的主要论文<<On Triangle>>(论三角形)(见第44页)中包括它——也没有包括正切函数的任何其他应用。至于正切法则的其它发现,参见David Eugene Smith的<<History of Mathematics>>(数学史)(1925初版; New York: Dover, 1958重印)。
4. 三角学中大量存在(abounds)这样的例子。在第8章中我们已经见到了一个与 sinα + sin(2α) + ... + sin(nα) 的求和公式相关的内容。另一个例子是恒等式
,
可通过将左侧写成
的方式予以“证明”。
5. 我们可以考虑将 (其中
)扩展来考虑符号。
6. 这相当于更熟悉的形如(x - xi![]() )因式分解成的因子。例如,多项式
)因式分解成的因子。例如,多项式
的函数零值点是-2和3 ,因此,我们有f(x) = (x + 2)( x - 3) = -6(1 + x/2)( 1- x /3)。一般地,多项式
可以写成
(其中
是前导系数),或写成
)(其中,
是常数项)。
7. 实际上,Euler丢弃了x = 0 的根,并因此获得了 的无限积。参见Morris Kline的著作<<Mathematical Thought from Ancient to Modern Times>>(古今数学思想)( New York: Oxford University Press, 1972年版)卷2第448-449页。
8. 参见<<A Source Book in Mathematics>>(一部数学原始资料书),1200-1800年,编辑D. J. Struik(Cambridge, Mass.: Harvard University Press, 1969年版),第244-253页,对于等式(6)和(7)的严密证明,参见Richard Courant的著作<<Differential and Integral Calculus>>(微积分)( London: Blackie & Son, 1956年版),卷1第444-445页和223-224页。π的其它无限积也可以通过等式(6)推断;例如,代入 x = π/6,我们得到
,
它实际上比Wallis积收敛得更快(与Wallis积的 493 项相比,该积近似π接近小数点后两位需要55项)。
9. 然而,随着 i 的增加,所得的数值积变得更加复杂。幸运的是,有一种更简单的方法可以找到系数:等式(11)的左侧是 sinx,而右侧的每一项等于cosx 除以该项缺失的分母。因此,为了求得 ,在等式(11)中代入 x = 3π/2;这将“消灭掉(annihilate)”除A2
![]() 的所有项,因此,我们得到剩下的项
的所有项,因此,我们得到剩下的项 。
左侧等于-1,但是,在右侧我们得到了不确定表达式 00![]() 。为了计算它,我们使用洛必达法则(L'Hospital's Rule)并将其转换为
。为了计算它,我们使用洛必达法则(L'Hospital's Rule)并将其转换为 。
因此,我们求得 。以同样的方式可以求得其它系数。
10. 参见Petr Beckmann的著作<<A History of π>>(数π的历史)( Boulder, Colo.: Golem Press,1977),第132-133页;对于Leibniz的证明,参见George F. Simmons的著作<< Calculus with Analytic Geometry>>(带解析几何的微积分)( New York: McGraw-Hill, 1985),第720-721页。 的级数可以通过将表达式
写成幂级数(具有商-
的几何级数)并逐项融合的方式求得。
11. 级数 1/5 + 1/21 + 1/45 + ...收敛于1/3, 注意到,其每一项符合通式
,这可以确认其收敛于1/3;因此,级数变成了(1/4)[(1-1/5) + (1/3-1/7) + (1/5-1/9) + (1/7-1/11) + ...]。这是一个“套叠式(telescopic)”的级数,在其中,除了第一项和最后一项,其它所有项都被消掉了,最终和为(1/4)(1 + 1/3) = 1/3 。
12. 当然,假设该级数收敛。在微积分课本中,证明了级数 (其中 k 是一个实数)对于所有 k > 1 的实数收敛,而对于所有 k ≤1 的实数发散,这里对应的情况是 k = 2,因此 S 收敛。
13. 参见Simmons的<<Calculus>>(微积分)第722-726页(Euler的证明)以及723-725(一种严密的证明)。有人会认为级数 比 Gregory-Leibniz 级数收敛得快,理由是其所有项都是正值且包括整数平方。让人诧异的是,事实并非如此:其占到 628 项才能近似到π的小数点后两位精度,而Gregory-Leibniz 级数近似到π的小数点后两位精度需要600 项。
14. ,最后的结果推断于
,
其中,u = 1/ t。
15. 有人会质疑等式(17)根据自己来表达π,因为切线项中的角度以弧度表示。但是,三角函数不受角度单位选择的影响;使用度数而不是弧度,等式(17)变为 1/π = (1/4)tan 45°+ (1/8)tan (45°/2) + ...。
16. 关于这个主题,参见Kline的“数学思想”卷2第442-445页以及460-467页。另可参见我的另一本书<<To Infinity and Beyond: A Cultural History of the Infinite>>(无限与超越:无限的文化史) (Princeton, N.J.: Princeton University Press, 1991年出版)第32-33页以及36-39页。
17. Simmons的“微积分”的第723页。
内容来源:
<<Trigonometric Delights>> 作者:Eli Maor
相关文章:
趣味三角——第12章——tanx
第12章节 tanx In his very numerous memoires, and especially in his great work, Introductio in analysin infinitorum (1748), Euler displayed the most wonderful skill in obtaining a rich harvest of results of great interest. . . . Hardly any other work …...
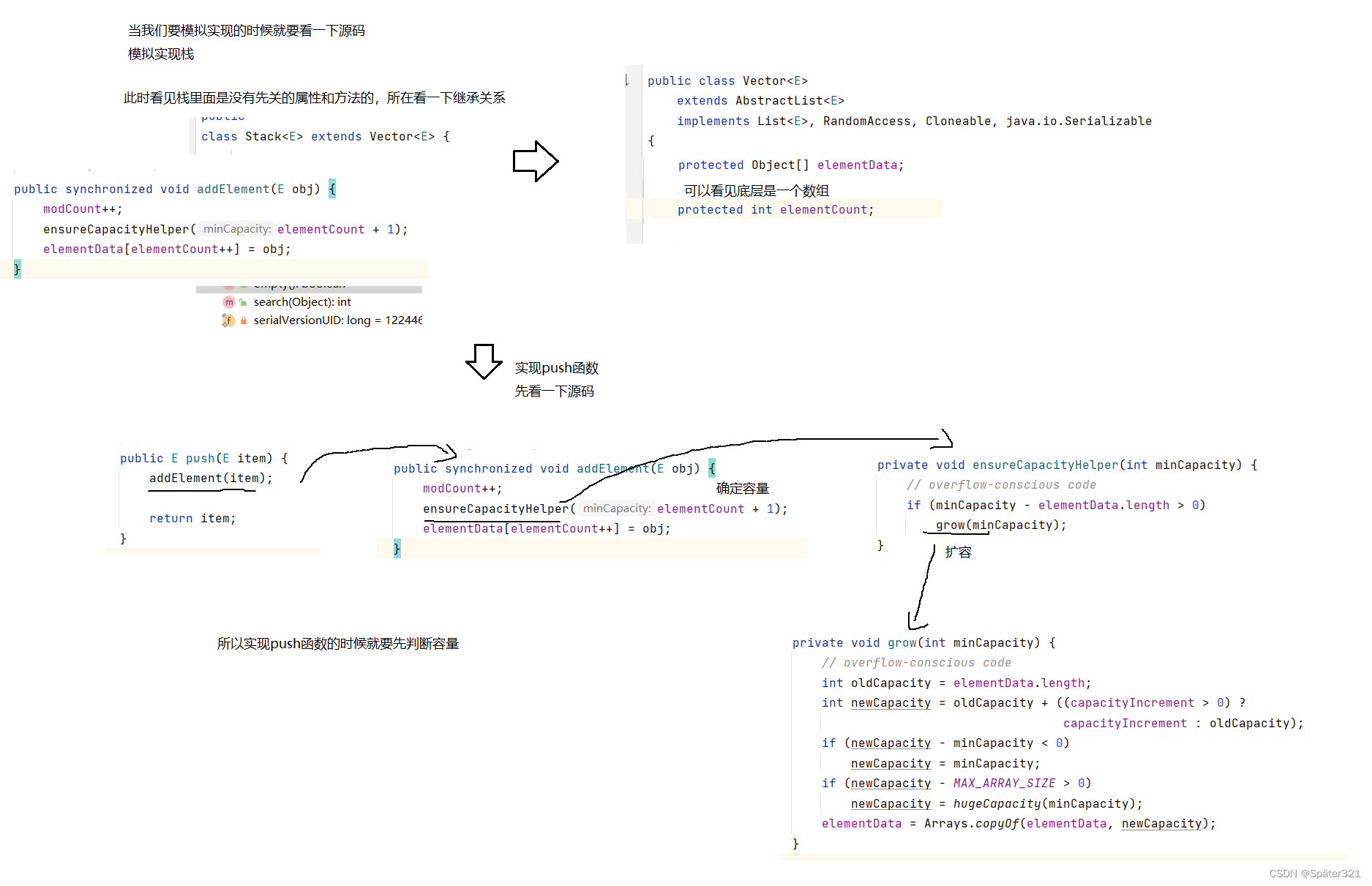
Java - 数据结构,栈
一、栈 1.1、什么是栈 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压…...
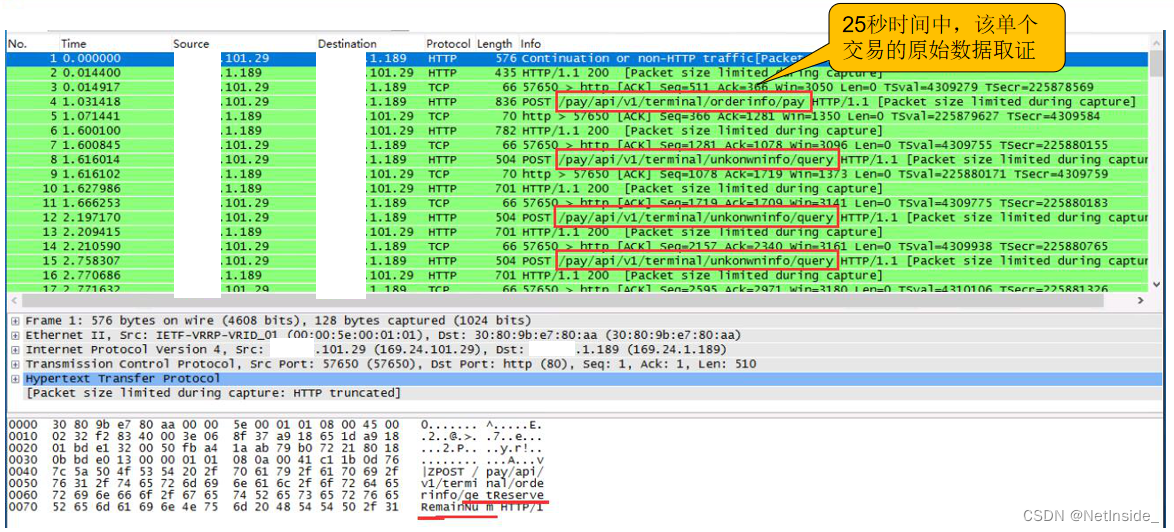
某餐厅系统网络故障分析案例
背景 针对食堂经营企业,某堂食软件为客户提供优化堂食就餐流程、提高食堂服务水平和管理效率。 某上海客户使用该堂食系统,在就餐高峰时段,总是出现支付、点餐等操作缓慢,动辄一个操作需要等待几十秒。该客户联系软件厂商&#…...

华为OD机试题,用 Java 解【密室逃生游戏】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

如何重命名SQL Server数据库
重命名SQL Server数据库 使用T-SQL重命名SQL Server数据库使用分离和附加重命名SQL Server数据库使用T-SQL查询分离和重新连接在SSMS中分离和重新连接通过SSMS重命名SQL Server数据库当使用SQL数据库很长一段时间时,你可能会遇到需要为数据库命名的情况。它可以用几种不同的方…...

联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?
联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?有用户电脑正常开机之后,出现了屏幕变成绿屏,无法进行操作的情况。这个问题是系统出现了问题,那么如何去进行问题的解决呢?接下来我们一起来分享看看如何使用U盘重装电脑…...
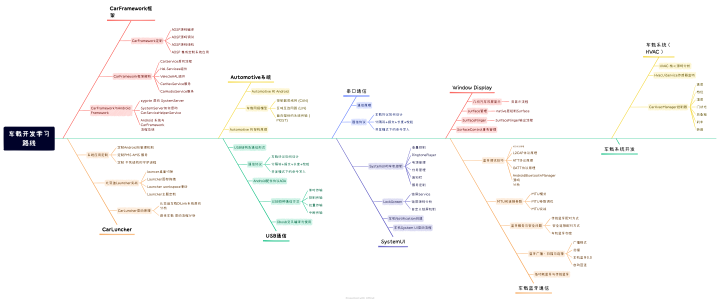
车载开发知识交流【学习路线】
前言 在2023国内百废待兴;经济复苏的号召一直在响应,这对于压抑了三年的人民来说无疑是福音。这篇我们主要说一下拉动经济的其中大板块——车企;我们知道我们最大的经济除了房地产,第二就是车企。而在造车领域中也不断的加入了许…...

【读书笔记】《深入浅出数据分析》第二章 检验你的理论
文章目录一,相关分析方法1,相关系数二,相关性不等于因果关系三,证明因果关系,“控制变量法”?本章主要说明了两个问题: 1,相关性不等于因果关系 2,如何判断两种数据之间是相关性&am…...
:table_apisql)
pyflink学习笔记(一):table_apisql
具体定义请参考官方文档:https://nightlies.apache.org/flink/flink-docs-release-1.16/zh/docs/dev/table/overview/本文主要针对实际使用中比较常用的api进行整理,大多数例子都是官网,如有歧义可与官方对照。一、 创建 TableEnvironmentTab…...

GCC 编译器套件说明
写在前面: 本文章旨在总结备份、方便以后查询,由于是个人总结,如有不对,欢迎指正;另外,内容大部分来自网络、书籍、和各类手册,如若侵权请告知,马上删帖致歉。 目录GCC 简述GCC 主要…...
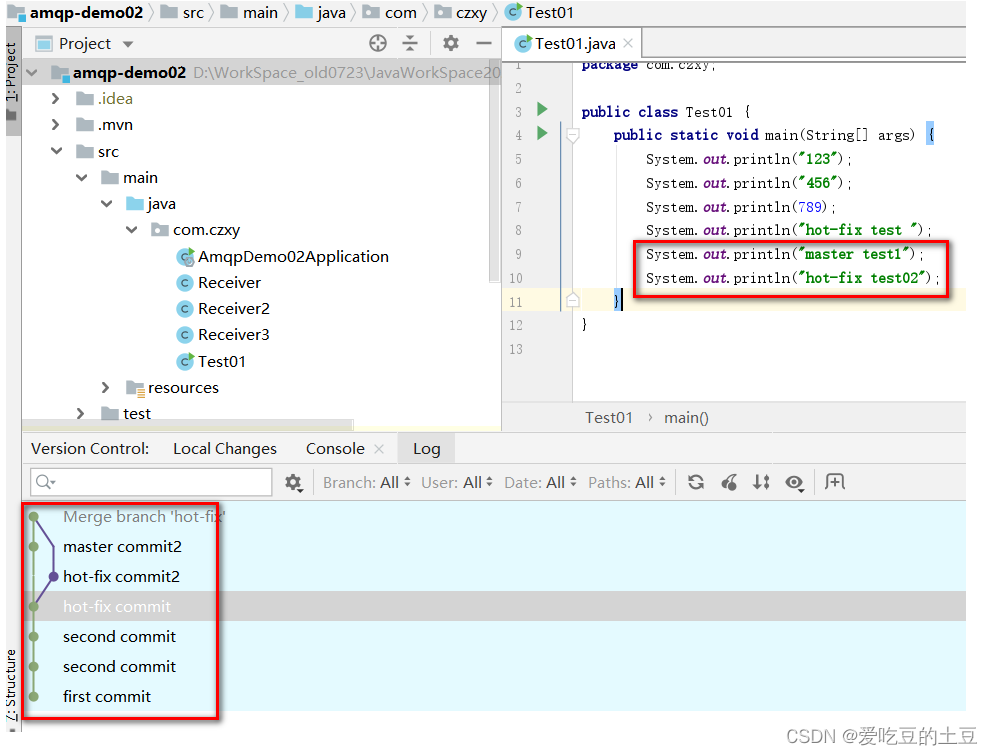
IDEA集成Git
1:IDEA集合Git1.1:配置Git忽略文件-IDEA特定文件问题 1:为什么要忽略他们?答: 与项目的实际功能无关, 不参与服务器上部署运行。把它们忽略掉能够屏蔽 IDE 工具之间的差异。问题 2:怎么忽略?1&a…...

算法流程图
里程计定位: 优:定位信息连续,无离散的跳跃 缺:存在累计误差,不利于长距或长期定位 传感器定位: 优:比里程计定位更精准 缺:会出现跳变情况,且传感器定位在标志物较少的环…...
Java中安装JDK环境–javac命令无效
Java中安装JDK环境–javac命令无效 一,安装JDK1.8 阿里云盘地址推荐 我们可以选择安装地址,这个地址是我们用来配置环境变量的,唯一注意的是这个,其他的都是默认下一步。直至安装完成,jdk下载地址https://www.oracl…...

递推问题
递推:在面对一个大任务的时候,有时候我们可以将大任务划分为小任务,再将小任务划分为更小的任务......,直到遇到初始情况,最后由初始情况一直往前推进,最后解决大任务,这就是递推的思想。递推问…...

js中强制类型转换Number、parseInt、parseFloat、Boolean、String、toString的使用
文章目录一、Number() 转换为整数二、Number.parseInt() 将字符串转换为整数三、Number.parseFloat() 将字符串转换为浮点数四、Boolean() 转换为布尔值五、String() 转换为字符串六、.toString() 转换为字符串最近在巩固 js 的基础知识,今天复习到了 js 中的数据类…...
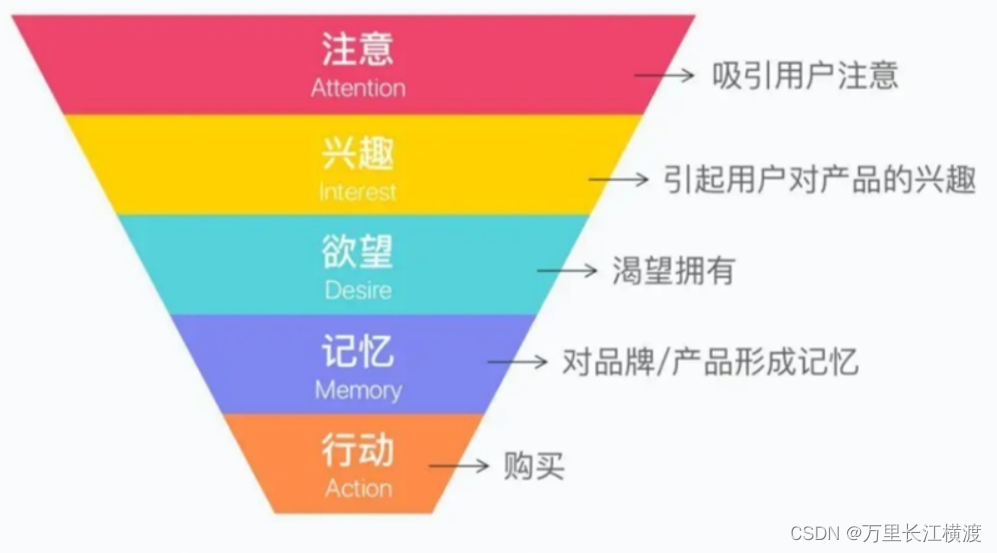
漏斗分析法
一什么是漏斗分析? 漏斗分析是数据领域最常见的一种“程式化”数据分析方法,它能够科学地评估一种业务过程,从起点到终点,各个阶段的转化情况。通过可以量化的数据分析,帮助业务找到有问题的业务环节,并进…...
)
pycharm入门快捷操作(部分)
altenter:提示意图动作shift两次或者crtlshifta:查找框(查找动作、类、项目等)crtlw:一次一个字符、两次整个字符串(if条件下选择整个判断体)、三次整个句子、四次整个引用ctrlshiftw࿱…...

宣布 Databricks 支持 Amazon Graviton2,性价比提高3倍
今天,我们很高兴地宣布 Databricks 对基于 Amazon Graviton2 的亚马逊弹性计算云(Amazon EC2)实例的支持的公开预览。Graviton 处理器由亚马逊云科技进行定制设计和优化,为运行在 Amazon EC2 上的云工作负载提供最佳性价比。当与高…...
18_FreeRTOS任务通知
目录 任务通知的简介 任务通知值的更新方式 任务通知的优势 任务通知的劣势 任务通知值和通知状态 发送通知相关API函数 接收通知相关API函数 任务通知模拟信号量实验 任务通知模拟消息邮箱实验 任务通知模拟事件标志组实验 任务通知的简介 任务通知:用来通知任务的…...

【华为OD机试模拟题】用 C++ 实现 - 整理扑克牌(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...

宠物车载安全座椅市场报告:解读行业趋势与投资前景
一、什么是宠物车载安全座椅? 宠物车载安全座椅是一种专为宠物设计的车内固定装置,旨在保障宠物在乘车过程中的安全性与舒适性。它通常由高强度材料制成,具备良好的缓冲性能,并可通过安全带或ISOFIX接口固定于车内。 近年来&…...
