数据挖掘实验（二）数据预处理【等深分箱与等宽分箱】
一、分箱平滑的原理
（1）分箱方法
在分箱前，一定要先排序数据，再将它们分到等深（等宽）的箱中。
常见的有两种分箱方法：等深分箱和等宽分箱。
等深分箱：按记录数进行分箱，每箱具有相同的记录数，每箱的记录数称为箱的权重，也称箱子的深度。
等宽分箱：在整个属性值的区间上平均分布，即每个箱的区间范围设定为一个常量，称为箱子的宽度。
（2）数据平滑
将数据划分到不同的箱子之后，可以运用如下三种策略对每个箱子中的数据进行平滑处理：
平均值平滑：箱中的每一个值被箱中数值的平均值替换。
中值平滑：箱中的每一个值被箱中数值的中值替换。
边界平滑：箱中的最大值和最小值称为箱子的边界，箱中的每一个值被最近的边界值替换。
二、Matlab代码实现
首先用rand()函数随机生成20*5的矩阵，其数据范围为[0,1]。
1.等深分箱
clear;clc; % 清除变量和命令窗口A=rand(20,5); % 随机生成20*5的矩阵，其中每个数取值范围[0,1]
fprintf("当前生成的原数据：\n");
disp(A);% 排序，参数1表示按列排序，取2为按行排序；'ascend'为升序，'descend'为降序
A=sort(A,1,'ascend');
fprintf("将原数据的每列排序后：\n");
disp(A);h=input("请输入等深分箱的深度h(1<h<20)：");% 检查输入变量h是否有效
if ~isnumeric(h) || ~isscalar(h) || h<=1 || h>=20 || h~=floor(h)error("输入变量h必须是一个大于1小于20的正整数");
end%% 对每列进行等深分箱，然后求每个箱子的均值
[n,m]=size(A); % n行m列
B=zeros(n,m); % 预分配输出变量B
for j=1:m % 列jfor i=1:h:n % 行i% 当前箱子第一个数位置为i，最后一个数位置为min(i+h-1,n)p1=int64(i); % 转换成整数(i默认是double类型，但是索引必须要为整数)p2=int64(min(i+h-1,n));B(p1:p2,j)=mean(A(p1:p2,j)); % 当前箱子的均值end
end % 结束行循环fprintf("\n经过等深分箱，用箱均值平滑处理后的数据：\n");
disp(B);
for i=1:h:n 的含义是：
- i 是一个循环变量，它的初始值是 1。
- h 是一个输入变量，它表示等深分箱的深度。
- n 是一个由 size 函数得到的变量，它表示矩阵 A 的行数。
- 这个循环的作用是从第一行开始，每隔 h 行取一行作为一个箱子的起始位置，然后计算这个箱子中所有元素的均值，并赋给输出矩阵 B 的相应位置。
isnumeric 函数是一个用于判断输入是否为数值数组的函数。数值数组是指由数值类型的元素组成的数组，例如整数、浮点数、无穷大或非数字。MATLAB 中的数值类型包括 int8, int16, int32, int64, uint8, uint16, uint32, uint64, single, 和 double。
isnumeric 函数的语法格式是：
TF = isnumeric(A)其中，A 是输入数组，可以是任意维度的；TF 是输出逻辑值，如果 A 是数值数组，则返回 1 (true)，否则返回 0 (false)。
例如，如果 A 是一个包含整数和浮点数的矩阵，那么 isnumeric(A) 将返回 1；如果 A 是一个包含字符串或单元数组的矩阵，那么 isnumeric(A) 将返回 0。
~isscalar(h) 函数是一个逻辑表达式，它用于判断 h 是否不是一个标量。标量是一个大小为 1×1 的二维数组，也就是一个单个的数值。如果 h 不是一个标量，那么 ~isscalar(h) 将返回 1 (true)，否则返回 0 (false)。
python代码为
import numpy as np # 导入 numpy 库
=A = np.random.rand(20,5) # 随机生成 20*5 的矩阵，其中每个数取值范围 [0,1]
print("当前生成的原数据：")
print(A)# 排序，参数 0 表示按列排序，取 1 为按行排序；'ascend' 为升序，'descend' 为降序
A = np.sort(A, axis=0, kind='quicksort') # 使用快速排序算法
print("将原数据的每列排序后：")
print(A)h = int(input("请输入等深分箱的深度 h (1<h<20)：")) # 输入一个整数# 检查输入变量 h 是否有效
if not isinstance(h, int) or h <= 1 or h >= 20: # 如果 h 不是一个大于 1 小于 20 的整数raise ValueError("输入变量 h 必须是一个大于 1 小于 20 的正整数") # 抛出异常# 对每列进行等深分箱，然后求每个箱子的均值
n, m = A.shape # n 行 m 列
B = np.zeros((n,m)) # 预分配输出变量 B
for j in range(m): # 列 jfor i in range(0, n, h): # 行 i# 当前箱子第一个数位置为 i，最后一个数位置为 min(i+h,n)p1 = int(i) # 转换成整数 (i 默认是 double 类型，但是索引必须要为整数)p2 = int(min(i+h,n))B[p1:p2,j] = np.mean(A[p1:p2,j]) # 当前箱子的均值print("\n经过等深分箱，用箱均值平滑处理后的数据：")
print(B)
代码运行结果
输入的深度为3：
当前生成的原数据：
A =0.4067 0.4504 0.5747 0.5154 0.99690.6669 0.2057 0.3260 0.6575 0.55350.9337 0.8997 0.4564 0.9509 0.51550.8110 0.7626 0.7138 0.7223 0.33070.4845 0.8825 0.8844 0.4001 0.43000.7567 0.2850 0.7209 0.8319 0.49180.4170 0.6732 0.0186 0.1343 0.07100.9718 0.6643 0.6748 0.0605 0.88770.9880 0.1228 0.4385 0.0842 0.06460.8641 0.4073 0.4378 0.1639 0.43620.3889 0.2753 0.1170 0.3242 0.82660.4547 0.7167 0.8147 0.3017 0.39450.2467 0.2834 0.3249 0.0117 0.61350.7844 0.8962 0.2462 0.5399 0.81860.8828 0.8266 0.3427 0.0954 0.88620.9137 0.3900 0.3757 0.1465 0.93110.5583 0.4979 0.5466 0.6311 0.19080.5989 0.6948 0.5619 0.8593 0.25860.1489 0.8344 0.3958 0.9742 0.89790.8997 0.6096 0.3981 0.5708 0.5934将原数据的每列排序后：
A =0.1489 0.1228 0.0186 0.0117 0.06460.2467 0.2057 0.1170 0.0605 0.07100.3889 0.2753 0.2462 0.0842 0.19080.4067 0.2834 0.3249 0.0954 0.25860.4170 0.2850 0.3260 0.1343 0.33070.4547 0.3900 0.3427 0.1465 0.39450.4845 0.4073 0.3757 0.1639 0.43000.5583 0.4504 0.3958 0.3017 0.43620.5989 0.4979 0.3981 0.3242 0.49180.6669 0.6096 0.4378 0.4001 0.51550.7567 0.6643 0.4385 0.5154 0.55350.7844 0.6732 0.4564 0.5399 0.59340.8110 0.6948 0.5466 0.5708 0.61350.8641 0.7167 0.5619 0.6311 0.81860.8828 0.7626 0.5747 0.6575 0.82660.8997 0.8266 0.6748 0.7223 0.88620.9137 0.8344 0.7138 0.8319 0.88770.9337 0.8825 0.7209 0.8593 0.89790.9718 0.8962 0.8147 0.9509 0.93110.9880 0.8997 0.8844 0.9742 0.9969请输入等深分箱的深度h(1<h<20)：3经过等深分箱，用箱均值平滑处理后的数据：
B =0.2615 0.2013 0.1273 0.0521 0.10880.2615 0.2013 0.1273 0.0521 0.10880.2615 0.2013 0.1273 0.0521 0.10880.4262 0.3195 0.3312 0.1254 0.32790.4262 0.3195 0.3312 0.1254 0.32790.4262 0.3195 0.3312 0.1254 0.32790.5472 0.4519 0.3899 0.2633 0.45270.5472 0.4519 0.3899 0.2633 0.45270.5472 0.4519 0.3899 0.2633 0.45270.7360 0.6490 0.4443 0.4851 0.55410.7360 0.6490 0.4443 0.4851 0.55410.7360 0.6490 0.4443 0.4851 0.55410.8526 0.7247 0.5611 0.6198 0.75290.8526 0.7247 0.5611 0.6198 0.75290.8526 0.7247 0.5611 0.6198 0.75290.9157 0.8478 0.7031 0.8045 0.89060.9157 0.8478 0.7031 0.8045 0.89060.9157 0.8478 0.7031 0.8045 0.89060.9799 0.8979 0.8495 0.9626 0.96400.9799 0.8979 0.8495 0.9626 0.9640
2.等宽分箱
输入箱子的宽度w(0<w<1)，将每列按等宽分箱，然后用箱均值平滑。
clear;clc; % 清除变量和命令窗口%A=rand(20,5); % 随机生成20*5的矩阵，其中每个数取值范围[0,1]
A=[ 0.5038 0.3600 0.6690 0.1432 0.94190.6128 0.4542 0.5002 0.5594 0.65590.8194 0.3864 0.2180 0.0046 0.45190.5319 0.7756 0.5716 0.7667 0.83970.2021 0.7343 0.1222 0.8487 0.53260.4539 0.4303 0.6712 0.9168 0.55390.4279 0.6938 0.5996 0.9870 0.68010.9661 0.9452 0.0560 0.5051 0.36720.6201 0.7842 0.0563 0.2714 0.23930.6954 0.7056 0.1525 0.1008 0.57890.7202 0.1093 0.0196 0.5078 0.86690.3469 0.3899 0.4352 0.5856 0.40680.5170 0.5909 0.8322 0.7629 0.11260.5567 0.4594 0.6174 0.0830 0.44380.1565 0.0503 0.5201 0.6616 0.30020.5621 0.2287 0.8639 0.5170 0.40140.6948 0.8342 0.0977 0.1710 0.83340.4265 0.0156 0.9081 0.9386 0.40360.8363 0.8637 0.1080 0.5905 0.39020.7314 0.0781 0.5170 0.4406 0.3604];
fprintf("当前生成的原数据：\n");
disp(A);
% 排序，参数1表示按列排序，取2为按行排序；'ascend'为升序，'descend'为降序
A=sort(A,1,'ascend');
fprintf("将原数据的每列排序后：\n");
disp(A);w=input("请输入等宽分箱的宽度w(0<w<1)：");
% 检查输入变量w是否有效
if ~isnumeric(w) || ~isscalar(w) || w<=0error("输入变量w必须是一个大于0小于1的正数");
end%% 对每列进行等宽分箱，然后求每个箱子的均值
[n,m]=size(A); % n行m列
B=zeros(n,m); % 预分配输出变量B
for j=1:m % 列jpos=1; % 当前箱子第一个数的位置A(n+1,j)=18e9; % 保证i=n+1时，A(i,j)-A(pos,j)>w一定成立for i=1:n+1 % 行iif A(i,j)-A(pos,j)>w % 当前箱子最后一个数的位置为i-1B(pos:i-1,j)=mean(A(pos:i-1,j)); % 当前箱子的均值pos=i; % 更新为下一个箱子的第一个数的位置endend
endfprintf("\n经过等宽分箱，用箱均值平滑处理后的数据：\n");
disp(B);if A(i,j)-A(pos,j)>w
这段代码的作用是判断当前元素是否属于当前箱子。如果当前元素与当前箱子的第一个元素的差大于 w，那么说明当前元素已经超出了当前箱子的范围，需要开始新的一个箱子；如果不大于 w，那么说明当前元素还在当前箱子内，继续循环。
代码运行结果
输入的宽度为0.2：
当前生成的原数据：
A =0.5038 0.3600 0.6690 0.1432 0.94190.6128 0.4542 0.5002 0.5594 0.65590.8194 0.3864 0.2180 0.0046 0.45190.5319 0.7756 0.5716 0.7667 0.83970.2021 0.7343 0.1222 0.8487 0.53260.4539 0.4303 0.6712 0.9168 0.55390.4279 0.6938 0.5996 0.9870 0.68010.9661 0.9452 0.0560 0.5051 0.36720.6201 0.7842 0.0563 0.2714 0.23930.6954 0.7056 0.1525 0.1008 0.57890.7202 0.1093 0.0196 0.5078 0.86690.3469 0.3899 0.4352 0.5856 0.40680.5170 0.5909 0.8322 0.7629 0.11260.5567 0.4594 0.6174 0.0830 0.44380.1565 0.0503 0.5201 0.6616 0.30020.5621 0.2287 0.8639 0.5170 0.40140.6948 0.8342 0.0977 0.1710 0.83340.4265 0.0156 0.9081 0.9386 0.40360.8363 0.8637 0.1080 0.5905 0.39020.7314 0.0781 0.5170 0.4406 0.3604将原数据的每列排序后：
A =0.1565 0.0156 0.0196 0.0046 0.11260.2021 0.0503 0.0560 0.0830 0.23930.3469 0.0781 0.0563 0.1008 0.30020.4265 0.1093 0.0977 0.1432 0.36040.4279 0.2287 0.1080 0.1710 0.36720.4539 0.3600 0.1222 0.2714 0.39020.5038 0.3864 0.1525 0.4406 0.40140.5170 0.3899 0.2180 0.5051 0.40360.5319 0.4303 0.4352 0.5078 0.40680.5567 0.4542 0.5002 0.5170 0.44380.5621 0.4594 0.5170 0.5594 0.45190.6128 0.5909 0.5201 0.5856 0.53260.6201 0.6938 0.5716 0.5905 0.55390.6948 0.7056 0.5996 0.6616 0.57890.6954 0.7343 0.6174 0.7629 0.65590.7202 0.7756 0.6690 0.7667 0.68010.7314 0.7842 0.6712 0.8487 0.83340.8194 0.8342 0.8322 0.9168 0.83970.8363 0.8637 0.8639 0.9386 0.86690.9661 0.9452 0.9081 0.9870 0.9419请输入等宽分箱的宽度w(0<w<1)：0.2经过等宽分箱，用箱均值平滑处理后的数据：
B =0.2352 0.0633 0.1038 0.1005 0.21740.2352 0.0633 0.1038 0.1005 0.21740.2352 0.0633 0.1038 0.1005 0.21740.5213 0.0633 0.1038 0.1005 0.43120.5213 0.3413 0.1038 0.1005 0.43120.5213 0.3413 0.1038 0.3560 0.43120.5213 0.3413 0.1038 0.3560 0.43120.5213 0.3413 0.1038 0.5610 0.43120.5213 0.4837 0.5373 0.5610 0.43120.5213 0.4837 0.5373 0.5610 0.43120.5213 0.4837 0.5373 0.5610 0.43120.5213 0.4837 0.5373 0.5610 0.43120.5213 0.7702 0.5373 0.5610 0.43120.7496 0.7702 0.5373 0.5610 0.63830.7496 0.7702 0.5373 0.8467 0.63830.7496 0.7702 0.7591 0.8467 0.63830.7496 0.7702 0.7591 0.8467 0.87050.7496 0.7702 0.7591 0.8467 0.87050.7496 0.7702 0.7591 0.8467 0.87050.9661 0.9452 0.9081 0.9870 0.8705
相关文章：
数据挖掘实验（二）数据预处理【等深分箱与等宽分箱】
一、分箱平滑的原理 （1）分箱方法 在分箱前，一定要先排序数据，再将它们分到等深（等宽）的箱中。 常见的有两种分箱方法：等深分箱和等宽分箱。 等深分箱：按记录数进行分箱࿰…...
Vue2 第一次学习
本章为超级浓缩版,文章过于短,方便复习使用哦~ 文章目录 1. 简单引入 vue.js2. 指令2.1 事件绑定指令 v-on (简写 )2.2 内容渲染指令2.3 双向绑定指令 v-model2.4 属性绑定指令 v-bind (简写 : )2.5 条件渲染指令2.6 循环指令 v-for 3. vue 其他知识3.1 侦听器 watch3.2 计算属…...
tiny模式基本原理整合
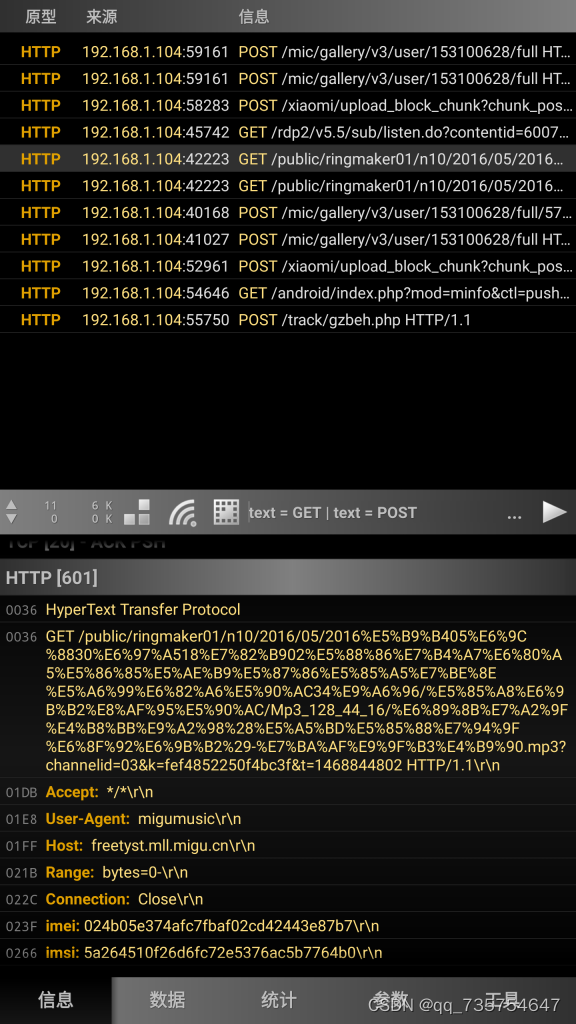
【Tiny模式】的基本构成 M【首头在首位】 U【/】 V【HTTP/】 Host H【真实ip】 XH \r回车 \n换行 \t制表 \ 空格 一个基本的模式构成 [method] [uri] [version]\r\nHost: [host]\r\n[method] [uri] [version]\r\nHost: [host]\r\n 检测顺序 http M H XH 有些地区 XH H M 我这边…...
使用聚氨酯密封件的好处?
聚氨酯密封件因其优异的耐用性、灵活性和广泛的应用范围而在各个行业中广受欢迎。在本文中，我们将探讨使用聚氨酯密封件的优点，阐明其在许多不同领域广泛使用背后的原因。 1、高性能： 聚氨酯密封件具有出色的性能特征，使其成为各…...
DevEco Studio如何安装中文插件
首先 官网下载中文插件 由于DevEco是基于IntelliJ IDEA Community的，所有Compatibility选择“IntelliJ IDEA Community”，然后下载一个对应最新的就ok了。 最后打开Plugins页面，点击右上角齿轮 -> Install Plugin from Disk…。选择下载的…...
10.2 校招 实习 内推 面经
绿泡*泡： neituijunsir 交流裙 ，内推/实习/校招汇总表格 1、校招 | 国家电网 国网信通产业集团2024届校园招聘！ 校招 | 国家电网 国网信通产业集团2024届校园招聘！ 2、校招 | 海信集团2024届全球校园招聘正式启动！…...
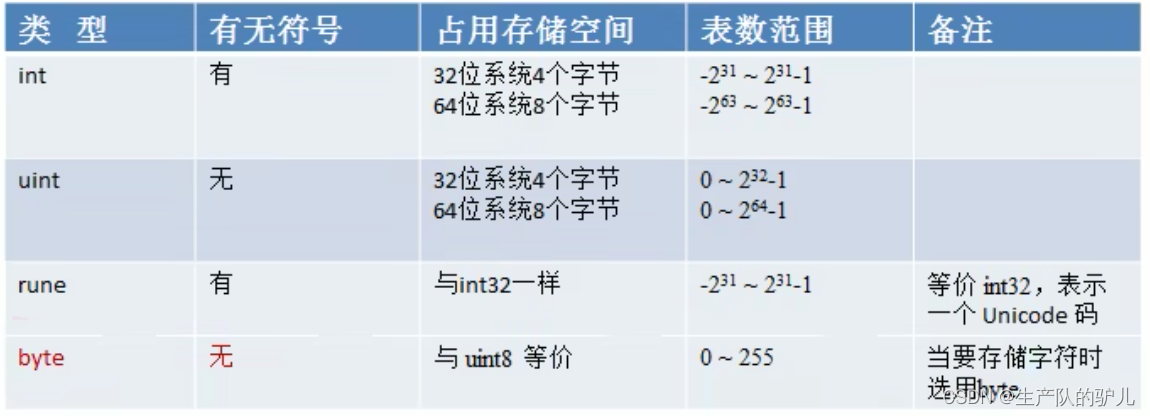
Golang 语言学习 01 包含如何快速学习一门新语言
Golang方向 区块链 go服务器端 (后台流量支撑程序) 支撑主站后台流量（排序，推荐，搜索等），提供负载均衡，cache，容错，按条件分流，统计运行指标 (qps， latenc…...
整理了197个经典SOTA模型，涵盖图像分类、目标检测、推荐系统等13个方向
今天来帮大家回顾一下计算机视觉、自然语言处理等热门研究领域的197个经典SOTA模型，涵盖了图像分类、图像生成、文本分类、强化学习、目标检测、推荐系统、语音识别等13个细分方向。建议大家收藏了慢慢看，下一篇顶会的idea这就来了~ 由于整理的SOTA模型…...
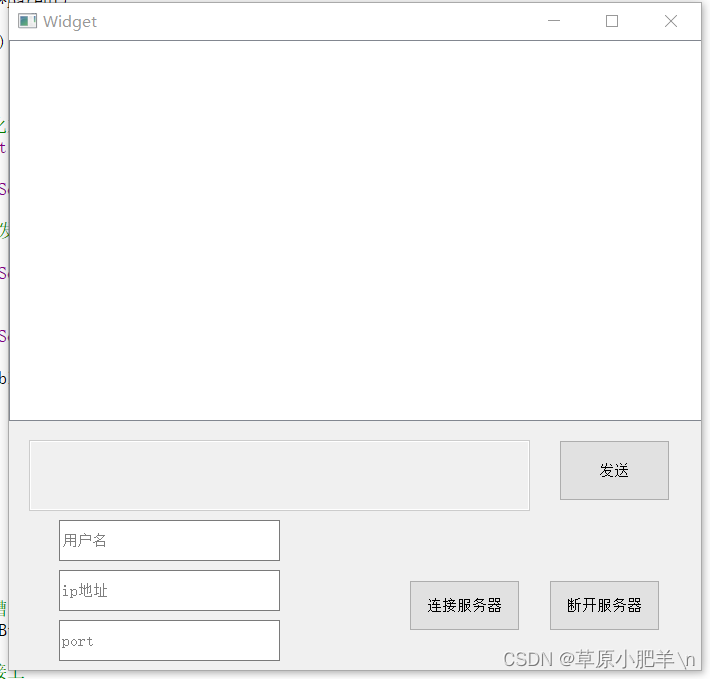
10.4 小任务
目录 QT实现TCP服务器客户端搭建的代码，现象 TCP服务器 .h文件 .cpp文件 现象 TCP客户端 .h文件 .cpp文件 现象 QT实现TCP服务器客户端搭建的代码，现象 TCP服务器 .h文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #includ…...
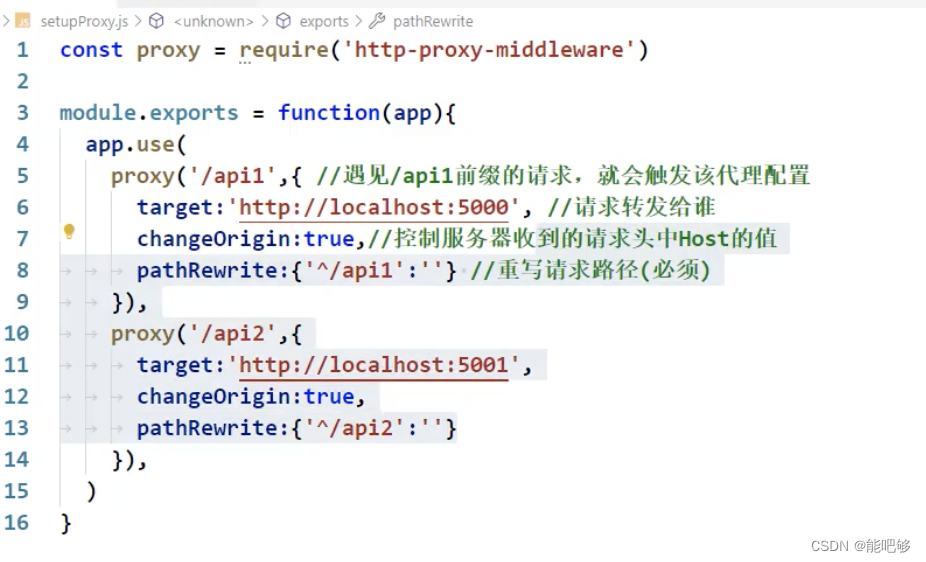
AJAX--Express速成
一、基本概念 1、AJAX(Asynchronous JavaScript And XML)，即为异步的JavaScript 和 XML。 2、异步的JavaScript 它可以异步地向服务器发送请求，在等待响应的过程中，不会阻塞当前页面。浏览器可以做自己的事情。直到成功获取响应后…...
开题报告 PPT 应该怎么做
开题报告 PPT 应该怎么做 1、报告时首先汇报自己的姓名、单位、专业和导师。 2、研究背景（2-3张幻灯片） 简要阐明所选题目的研究目的及意义。 研究的目的，即研究应达到的目标，通过研究的背景加以说明（即你为什么要…...
JavaScript系列从入门到精通系列第十四篇：JavaScript中函数的简介以及函数的声明方式以及函数的调用
文章目录 一：函数的简介 1：概念和简介 2：创建一个函数对象 3：调用函数对象 4：函数对象的普通功能 5：使用函数声明来创建一个函数对象 6：使用函数声明创建一个匿名函数 一：函…...
当我们做后仿时我们究竟在仿些什么（三）
异步电路之间必须消除毛刺 之前提到过，数字电路后仿的一个主要目的就是动态验证异步电路时序。异步电路的时序是目前STA工具无法覆盖的。 例如异步复位的release是同步事件，其时序是可以靠STA保证的；但是reset是异步事件，它的时序…...
如何将超大文件压缩到最小
1、一个文件目录，查看属性发现这个文件达到了2.50GB； 2、右键此目录选择添加到压缩文件； 3、在弹出的窗口中将压缩文件格式选择为RAR4，压缩方式选择为最好，选择字典大小最大，勾选压缩选项中的创建固实压缩&…...
[C#]C#最简单方法获取GPU显存真实大小
你是否用下面代码获取GPU显存容量？ using System.Management; private void getGpuMem() {ManagementClass c new ManagementClass("Win32_VideoController");foreach (ManagementObject o in c.GetInstances()){string gpuTotalMem String.For…...
【数据结构】红黑树(C++实现)
📝个人主页：Sherry的成长之路 🏠学习社区：Sherry的成长之路（个人社区） 📖专栏链接：数据结构 🎯长路漫漫浩浩，万事皆有期待 上一篇博客：【数据…...
day-64 代码随想录算法训练营（19）图论 part 03
827.最大人工岛 思路一：深度优先遍历 1.深度优先遍历，求出所有岛屿的面积，并且把每个岛屿记上不同标记2.使用 unordered_map 使用键值对，标记：面积，记录岛屿面积3.遍历所有海面，然后进行一次广…...
xss测试步骤总结
文章目录 测试流程1.开启burp2.测试常规xss语句3.观察回显4.测试闭合与绕过Level2Level3Level4Level5Level6Level7 5.xss绕过方法1)测试需观察点2)无过滤法3)">闭合4)单引号闭合事件函数5)双引号闭合事件函数6)引号闭合链接7)大小写绕过8)多写绕过9)unicode编码10)unic…...
2023最新简易ChatGPT3.5小程序全开源源码+全新UI首发+实测可用可二开（带部署教程）
源码简介： 2023最新简易ChatGPT3.5小程序全开源源码全新UI首发，实测可以用，而且可以二次开发。这个是最新ChatGPT智能AI机器人微信小程序源码，同时也带部署教程。 这个全新版本的小界面设计相当漂亮，简单大方&#x…...
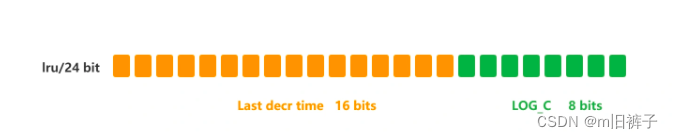
【Redis】数据过期策略和数据淘汰策略
数据过期策略和淘汰策略 过期策略 Redis所有的数据结构都可以设置过期时间，时间一到，就会自动删除。 问题：大家都知道，Redis是单线程的，如果同一时间太多key过期，Redis删除的时间也会占用线程的处理时间…...
在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中，手势开发全攻略：
在 HarmonyOS 应用开发中，手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力，既支持点击、长按、拖拽等基础单一手势的精细控制，也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档，…...
【论文笔记】若干矿井粉尘检测算法概述
总的来说，传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度，通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
MySQL 8.0 OCP 英文题库解析（十三）
Oracle 为庆祝 MySQL 30 周年，截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始，将英文题库免费公布出来，并进行解析，帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代，加密货币作为一种新兴的金融现象，正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而，加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下，稳定…...
Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中，CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时，通常会导致应用响应缓慢，甚至服务不可用，严重影响用户体验和业务运行。因此，掌握一套科学有效的CPU飙高问题排查方法&…...
AirSim/Cosys-AirSim 游戏开发（四）外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机，因为在使用过程中发现 Airsim 对外部监控相机的描述模糊，而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置，最后在源码示例中找到了，所以感…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象： android studio报错： [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决： 不要动CMakeLists.…...
探索Selenium：自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
软件工程 期末复习
瀑布模型：计划 螺旋模型：风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合：模块内部功能紧密 模块之间依赖程度小 高内聚：指的是一个模块内部的功能应该紧密相关。换句话说，一个模块应当只实现单一的功能…...