C#，数值计算——完全VEGAS编码的蒙特·卡洛计算方法与源程序
1 文本格式
using System;
namespace Legalsoft.Truffer
{
/// <summary>
/// Complete VEGAS Code
/// adaptive/recursive Monte Carlo
/// </summary>
public abstract class VEGAS
{
const int NDMX = 50;
const int MXDIM = 10;
const int RANSEED = 5330;
const double ALPH = 1.5;
const double TINY = 1.0e-30;
private Ran ran_vegas = new Ran(RANSEED);
//public static delegateFuncVectorDouble func_v_d { get; set; } = null;
public VEGAS()
{
}
public abstract double fxn(double[] x, double wgt);
public static void rebin(double rc, int nd, double[] r, double[] xin, double[,] xi, int j)
{
//int i;
int k = 0;
double dr = 0.0;
//double xn = 0.0;
double xo = 0.0;
for (int i = 0; i < nd - 1; i++)
{
while (rc > dr)
{
dr += r[(++k) - 1];
}
if (k > 1)
{
xo = xi[j, k - 2];
}
double xn = xi[j, k - 1];
dr -= rc;
xin[i] = xn - (xn - xo) * dr / r[k - 1];
}
for (int i = 0; i < nd - 1; i++)
{
xi[j, i] = xin[i];
}
xi[j, nd - 1] = 1.0;
}
/// <summary>
/// Performs Monte Carlo integration of a user-supplied ndim-dimensional
/// function fxn over a rectangular volume specified by regn[0..2 * ndim - 1], a
/// vector consisting of ndim "lower left" coordinates of the region followed
/// by ndim "upper right" coordinates.The integration consists of itmx
/// iterations, each with approximately ncall calls to the function.After each
/// iteration the grid is refined; more than 5 or 10 iterations are rarely
/// useful.The input flag init signals whether this call is a new start or a
/// subsequent call for additional iterations(see comments in the code). The
/// input flag nprn(normally 0) controls the amount of diagnostic output.
/// Returned answers are tgral (the best estimate of the integral), sd(its
/// standard deviation), and chi2a(X^2 per degree of freedom, an indicator of
/// whether consistent results are being obtained).
/// </summary>
/// <param name="regn"></param>
/// <param name="init"></param>
/// <param name="ncall"></param>
/// <param name="itmx"></param>
/// <param name="nprn"></param>
/// <param name="tgral"></param>
/// <param name="sd"></param>
/// <param name="chi2a"></param>
public void vegas(double[] regn, int init, int ncall, int itmx, int nprn, ref double tgral, ref double sd, ref double chi2a)
{
int mds = 0;
int ndo = 0;
double schi = 0.0;
double si = 0.0;
double swgt = 0.0;
int[] ia = new int[MXDIM];
int[] kg = new int[MXDIM];
double[] dt = new double[MXDIM];
double[] dx = new double[MXDIM];
double[] r = new double[NDMX];
double[] x = new double[MXDIM];
double[] xin = new double[NDMX];
double[,] d = new double[NDMX, MXDIM];
double[,] di = new double[NDMX, MXDIM];
double[,] xi = new double[MXDIM, NDMX];
//Ran ran_vegas = new Ran(RANSEED);
int ndim = regn.Length / 2;
if (init <= 0)
{
mds = ndo = 1;
for (int j = 0; j < ndim; j++)
{
xi[j, 0] = 1.0;
}
}
if (init <= 1)
{
si = swgt = schi = 0.0;
}
if (init <= 2)
{
int nd = NDMX;
int ng = 1;
if (mds != 0)
{
ng = (int)Math.Pow(ncall / 2.0 + 0.25, 1.0 / ndim);
mds = 1;
if ((2 * ng - NDMX) >= 0)
{
mds = -1;
int n1pg = ng / NDMX + 1;
nd = ng / n1pg;
ng = n1pg * nd;
}
}
int k = 1;
for (int i = 0; i < ndim; i++)
{
k *= ng;
}
int npg = Math.Max((int)(ncall / k), 2);
double calls = (double)npg * (double)k;
double dxg = 1.0 / ng;
double dv2g = 1.0;
for (int i = 0; i < ndim; i++)
{
dv2g *= dxg;
}
dv2g = Globals.SQR(calls * dv2g) / npg / npg / (npg - 1.0);
int xnd = nd;
dxg *= xnd;
double xjac = 1.0 / calls;
for (int j = 0; j < ndim; j++)
{
dx[j] = regn[j + ndim] - regn[j];
xjac *= dx[j];
}
if (nd != ndo)
{
for (int i = 0; i < Math.Max(nd, ndo); i++)
{
r[i] = 1.0;
}
for (int j = 0; j < ndim; j++)
{
rebin(ndo / xnd, nd, r, xin, xi, j);
}
ndo = nd;
}
if (nprn >= 0)
{
/*
Console.Write(" Input parameters for vegas");
Console.Write(" ndim= ");
Console.Write("{0,4}", ndim);
Console.Write("{0,4}", " ncall= ");
Console.Write("{0,8}", calls);
Console.Write("{0}", "\n");
Console.Write("{0,34}", " it=");
Console.Write("{0,5}", it);
Console.Write("{0,5}", " itmx=");
Console.Write("{0,5}", itmx);
Console.Write("{0}", "\n");
Console.Write("{0,34}", " nprn=");
Console.Write("{0,5}", nprn);
Console.Write("{0,5}", " ALPH=");
Console.Write("{0,9}", ALPH);
Console.Write("{0}", "\n");
Console.Write("{0,34}", " mds=");
Console.Write("{0,5}", mds);
Console.Write("{0,5}", " nd=");
Console.Write("{0,5}", nd);
Console.Write("{0}", "\n");
for (j = 0; j < ndim; j++)
{
Console.Write("{0,30}", " x1[");
Console.Write("{0,2}", j);
Console.Write("{0,2}", "]= ");
Console.Write("{0,11}", regn[j]);
Console.Write("{0}", " xu[");
Console.Write("{0,2}", j);
Console.Write("{0}", "]= ");
Console.Write("{0,11}", regn[j + ndim]);
Console.Write("{0}", "\n");
}
*/
for (int it = 0; it < itmx; it++)
{
double ti = 0.0;
double tsi = 0.0;
for (int j = 0; j < ndim; j++)
{
kg[j] = 1;
for (int i = 0; i < nd; i++)
{
d[i, j] = di[i, j] = 0.0;
}
}
for (; ; )
{
double fb = 0.0;
double f2b = 0.0;
for (k = 0; k < npg; k++)
{
double w1gt = xjac;
for (int j = 0; j < ndim; j++)
{
double xn = (kg[j] - ran_vegas.doub()) * dxg + 1.0;
ia[j] = Math.Max(Math.Min((int)xn, NDMX), 1);
double xo;
double rc;
if (ia[j] > 1)
{
xo = xi[j, ia[j] - 1] - xi[j, ia[j] - 2];
rc = xi[j, ia[j] - 2] + (xn - ia[j]) * xo;
}
else
{
xo = xi[j, ia[j] - 1];
rc = (xn - ia[j]) * xo;
}
x[j] = regn[j] + rc * dx[j];
w1gt *= xo * xnd;
}
double f = w1gt * fxn(x, w1gt);
double f2 = f * f;
fb += f;
f2b += f2;
for (int j = 0; j < ndim; j++)
{
di[ia[j] - 1, j] += f;
if (mds >= 0)
{
d[ia[j] - 1, j] += f2;
}
}
}
f2b = Math.Sqrt(f2b * npg);
f2b = (f2b - fb) * (f2b + fb);
if (f2b <= 0.0)
{
f2b = TINY;
}
ti += fb;
tsi += f2b;
if (mds < 0)
{
for (int j = 0; j < ndim; j++)
{
d[ia[j] - 1, j] += f2b;
}
}
for (k = ndim - 1; k >= 0; k--)
{
kg[k] %= ng;
if (++kg[k] != 1)
{
break;
}
}
if (k < 0)
{
break;
}
}
tsi *= dv2g;
double wgt = 1.0 / tsi;
si += wgt * ti;
schi += wgt * ti * ti;
swgt += wgt;
tgral = si / swgt;
chi2a = (schi - si * tgral) / (it + 0.0001);
if (chi2a < 0.0)
{
chi2a = 0.0;
}
sd = Math.Sqrt(1.0 / swgt);
tsi = Math.Sqrt(tsi);
}
if (nprn >= 0)
{
/*
Console.Write(" iteration no. ");
Console.Write("{0,3}", (it + 1));
Console.Write("{0,3}", " : integral = ");
Console.Write("{0,14}", ti);
Console.Write("{0,14}", " +/- ");
Console.Write("{0,9}", tsi);
Console.Write("{0}", "\n");
Console.Write("{0}", " all iterations: ");
Console.Write("{0}", " integral =");
Console.Write("{0,14}", tgral);
Console.Write("{0}", "+-");
Console.Write("{0,9}", sd);
Console.Write("{0,9}", " chi**2/IT n =");
Console.Write("{0,9}", chi2a);
Console.Write("{0}", "\n");
if (nprn != 0)
{
for (j = 0; j < ndim; j++)
{
Console.Write("{0}", " DATA FOR axis ");
Console.Write("{0,2}", j);
Console.Write("{0}", "\n");
Console.Write("{0}", " X delta i X delta i");
Console.Write("{0}", " X deltai");
Console.Write("{0}", "\n");
for (i = nprn / 2; i < nd - 2; i += nprn + 2)
{
Console.Write("{0,8}", xi[j, i]);
Console.Write("{0,12}", di[i, j]);
Console.Write("{0,12}", xi[j, i + 1]);
Console.Write("{0,12}", di[i + 1, j]);
Console.Write("{0,12}", xi[j, i + 2]);
Console.Write("{0,12}", di[i + 2, j]);
Console.Write("{0,12}", "\n");
}
}
}
*/
}
for (int j = 0; j < ndim; j++)
{
double xo = d[0, j];
double xn = d[1, j];
d[0, j] = (xo + xn) / 2.0;
dt[j] = d[0, j];
for (int i = 2; i < nd; i++)
{
double rc = xo + xn;
xo = xn;
xn = d[i, j];
d[i - 1, j] = (rc + xn) / 3.0;
dt[j] += d[i - 1, j];
}
d[nd - 1, j] = (xo + xn) / 2.0;
dt[j] += d[nd - 1, j];
}
for (int j = 0; j < ndim; j++)
{
double rc = 0.0;
for (int i = 0; i < nd; i++)
{
if (d[i, j] < TINY)
{
d[i, j] = TINY;
}
r[i] = Math.Pow((1.0 - d[i, j] / dt[j]) / (Math.Log(dt[j]) - Math.Log(d[i, j])), ALPH);
rc += r[i];
}
rebin(rc / xnd, nd, r, xin, xi, j);
}
}
}
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{/// <summary>/// Complete VEGAS Code/// adaptive/recursive Monte Carlo/// </summary>public abstract class VEGAS{const int NDMX = 50;const int MXDIM = 10;const int RANSEED = 5330;const double ALPH = 1.5;const double TINY = 1.0e-30;private Ran ran_vegas = new Ran(RANSEED);//public static delegateFuncVectorDouble func_v_d { get; set; } = null;public VEGAS(){}public abstract double fxn(double[] x, double wgt);public static void rebin(double rc, int nd, double[] r, double[] xin, double[,] xi, int j){//int i;int k = 0;double dr = 0.0;//double xn = 0.0;double xo = 0.0;for (int i = 0; i < nd - 1; i++){while (rc > dr){dr += r[(++k) - 1];}if (k > 1){xo = xi[j, k - 2];}double xn = xi[j, k - 1];dr -= rc;xin[i] = xn - (xn - xo) * dr / r[k - 1];}for (int i = 0; i < nd - 1; i++){xi[j, i] = xin[i];}xi[j, nd - 1] = 1.0;}/// <summary>/// Performs Monte Carlo integration of a user-supplied ndim-dimensional/// function fxn over a rectangular volume specified by regn[0..2 * ndim - 1], a/// vector consisting of ndim "lower left" coordinates of the region followed/// by ndim "upper right" coordinates.The integration consists of itmx/// iterations, each with approximately ncall calls to the function.After each/// iteration the grid is refined; more than 5 or 10 iterations are rarely/// useful.The input flag init signals whether this call is a new start or a/// subsequent call for additional iterations(see comments in the code). The/// input flag nprn(normally 0) controls the amount of diagnostic output./// Returned answers are tgral (the best estimate of the integral), sd(its/// standard deviation), and chi2a(X^2 per degree of freedom, an indicator of/// whether consistent results are being obtained)./// </summary>/// <param name="regn"></param>/// <param name="init"></param>/// <param name="ncall"></param>/// <param name="itmx"></param>/// <param name="nprn"></param>/// <param name="tgral"></param>/// <param name="sd"></param>/// <param name="chi2a"></param>public void vegas(double[] regn, int init, int ncall, int itmx, int nprn, ref double tgral, ref double sd, ref double chi2a){int mds = 0;int ndo = 0;double schi = 0.0;double si = 0.0;double swgt = 0.0;int[] ia = new int[MXDIM];int[] kg = new int[MXDIM];double[] dt = new double[MXDIM];double[] dx = new double[MXDIM];double[] r = new double[NDMX];double[] x = new double[MXDIM];double[] xin = new double[NDMX];double[,] d = new double[NDMX, MXDIM];double[,] di = new double[NDMX, MXDIM];double[,] xi = new double[MXDIM, NDMX];//Ran ran_vegas = new Ran(RANSEED);int ndim = regn.Length / 2;if (init <= 0){mds = ndo = 1;for (int j = 0; j < ndim; j++){xi[j, 0] = 1.0;}}if (init <= 1){si = swgt = schi = 0.0;}if (init <= 2){int nd = NDMX;int ng = 1;if (mds != 0){ng = (int)Math.Pow(ncall / 2.0 + 0.25, 1.0 / ndim);mds = 1;if ((2 * ng - NDMX) >= 0){mds = -1;int n1pg = ng / NDMX + 1;nd = ng / n1pg;ng = n1pg * nd;}}int k = 1;for (int i = 0; i < ndim; i++){k *= ng;}int npg = Math.Max((int)(ncall / k), 2);double calls = (double)npg * (double)k;double dxg = 1.0 / ng;double dv2g = 1.0;for (int i = 0; i < ndim; i++){dv2g *= dxg;}dv2g = Globals.SQR(calls * dv2g) / npg / npg / (npg - 1.0);int xnd = nd;dxg *= xnd;double xjac = 1.0 / calls;for (int j = 0; j < ndim; j++){dx[j] = regn[j + ndim] - regn[j];xjac *= dx[j];}if (nd != ndo){for (int i = 0; i < Math.Max(nd, ndo); i++){r[i] = 1.0;}for (int j = 0; j < ndim; j++){rebin(ndo / xnd, nd, r, xin, xi, j);}ndo = nd;}if (nprn >= 0){/*Console.Write(" Input parameters for vegas");Console.Write(" ndim= ");Console.Write("{0,4}", ndim);Console.Write("{0,4}", " ncall= ");Console.Write("{0,8}", calls);Console.Write("{0}", "\n");Console.Write("{0,34}", " it=");Console.Write("{0,5}", it);Console.Write("{0,5}", " itmx=");Console.Write("{0,5}", itmx);Console.Write("{0}", "\n");Console.Write("{0,34}", " nprn=");Console.Write("{0,5}", nprn);Console.Write("{0,5}", " ALPH=");Console.Write("{0,9}", ALPH);Console.Write("{0}", "\n");Console.Write("{0,34}", " mds=");Console.Write("{0,5}", mds);Console.Write("{0,5}", " nd=");Console.Write("{0,5}", nd);Console.Write("{0}", "\n");for (j = 0; j < ndim; j++){Console.Write("{0,30}", " x1[");Console.Write("{0,2}", j);Console.Write("{0,2}", "]= ");Console.Write("{0,11}", regn[j]);Console.Write("{0}", " xu[");Console.Write("{0,2}", j);Console.Write("{0}", "]= ");Console.Write("{0,11}", regn[j + ndim]);Console.Write("{0}", "\n");}*/for (int it = 0; it < itmx; it++){double ti = 0.0;double tsi = 0.0;for (int j = 0; j < ndim; j++){kg[j] = 1;for (int i = 0; i < nd; i++){d[i, j] = di[i, j] = 0.0;}}for (; ; ){double fb = 0.0;double f2b = 0.0;for (k = 0; k < npg; k++){double w1gt = xjac;for (int j = 0; j < ndim; j++){double xn = (kg[j] - ran_vegas.doub()) * dxg + 1.0;ia[j] = Math.Max(Math.Min((int)xn, NDMX), 1);double xo;double rc;if (ia[j] > 1){xo = xi[j, ia[j] - 1] - xi[j, ia[j] - 2];rc = xi[j, ia[j] - 2] + (xn - ia[j]) * xo;}else{xo = xi[j, ia[j] - 1];rc = (xn - ia[j]) * xo;}x[j] = regn[j] + rc * dx[j];w1gt *= xo * xnd;}double f = w1gt * fxn(x, w1gt);double f2 = f * f;fb += f;f2b += f2;for (int j = 0; j < ndim; j++){di[ia[j] - 1, j] += f;if (mds >= 0){d[ia[j] - 1, j] += f2;}}}f2b = Math.Sqrt(f2b * npg);f2b = (f2b - fb) * (f2b + fb);if (f2b <= 0.0){f2b = TINY;}ti += fb;tsi += f2b;if (mds < 0){for (int j = 0; j < ndim; j++){d[ia[j] - 1, j] += f2b;}}for (k = ndim - 1; k >= 0; k--){kg[k] %= ng;if (++kg[k] != 1){break;}}if (k < 0){break;}}tsi *= dv2g;double wgt = 1.0 / tsi;si += wgt * ti;schi += wgt * ti * ti;swgt += wgt;tgral = si / swgt;chi2a = (schi - si * tgral) / (it + 0.0001);if (chi2a < 0.0){chi2a = 0.0;}sd = Math.Sqrt(1.0 / swgt);tsi = Math.Sqrt(tsi);}if (nprn >= 0){/*Console.Write(" iteration no. ");Console.Write("{0,3}", (it + 1));Console.Write("{0,3}", " : integral = ");Console.Write("{0,14}", ti);Console.Write("{0,14}", " +/- ");Console.Write("{0,9}", tsi);Console.Write("{0}", "\n");Console.Write("{0}", " all iterations: ");Console.Write("{0}", " integral =");Console.Write("{0,14}", tgral);Console.Write("{0}", "+-");Console.Write("{0,9}", sd);Console.Write("{0,9}", " chi**2/IT n =");Console.Write("{0,9}", chi2a);Console.Write("{0}", "\n");if (nprn != 0){for (j = 0; j < ndim; j++){Console.Write("{0}", " DATA FOR axis ");Console.Write("{0,2}", j);Console.Write("{0}", "\n");Console.Write("{0}", " X delta i X delta i");Console.Write("{0}", " X deltai");Console.Write("{0}", "\n");for (i = nprn / 2; i < nd - 2; i += nprn + 2){Console.Write("{0,8}", xi[j, i]);Console.Write("{0,12}", di[i, j]);Console.Write("{0,12}", xi[j, i + 1]);Console.Write("{0,12}", di[i + 1, j]);Console.Write("{0,12}", xi[j, i + 2]);Console.Write("{0,12}", di[i + 2, j]);Console.Write("{0,12}", "\n");}}}*/}for (int j = 0; j < ndim; j++){double xo = d[0, j];double xn = d[1, j];d[0, j] = (xo + xn) / 2.0;dt[j] = d[0, j];for (int i = 2; i < nd; i++){double rc = xo + xn;xo = xn;xn = d[i, j];d[i - 1, j] = (rc + xn) / 3.0;dt[j] += d[i - 1, j];}d[nd - 1, j] = (xo + xn) / 2.0;dt[j] += d[nd - 1, j];}for (int j = 0; j < ndim; j++){double rc = 0.0;for (int i = 0; i < nd; i++){if (d[i, j] < TINY){d[i, j] = TINY;}r[i] = Math.Pow((1.0 - d[i, j] / dt[j]) / (Math.Log(dt[j]) - Math.Log(d[i, j])), ALPH);rc += r[i];}rebin(rc / xnd, nd, r, xin, xi, j);}}}}}
}
相关文章：
C#，数值计算——完全VEGAS编码的蒙特·卡洛计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Complete VEGAS Code /// adaptive/recursive Monte Carlo /// </summary> public abstract class VEGAS { const int NDMX 50; const int …...
纯css实现3D鼠标跟随倾斜
老规矩先上图 为什么今天会想起来整这个呢?这是因为和我朋友吵架, 就是关于这个效果的,就是这个 卡片懸停毛玻璃效果, 我朋友认为纯css也能写, 我则坦言他就是在放狗屁,这种跟随鼠标的3D效果要怎么可能能用纯css写, 然后吵着吵着发现,欸,好像真能用css写哦,我以前还写过这种…...
Pandas数据结构
文章目录 1. Series数据结构1.1 Series数据类型创建1.2 Series的常用属性valuesindex/keys()shapeTloc/iloc 1.3 Series的常用方法mean()max()/min()var()/std()value_counts()describe() 1.4 Series运算加/减法乘法 2. DataFrame数据结构2.1 DataFrame数据类型创建2.2 布尔索引…...
systemverilog function的一点小case
关于function的应用无论是在systemverilog还是verilog中都有很广泛的应用，但是一直有一个模糊的概念困扰着我，今天刚好有时间来搞清楚并记录下来。 关于fucntion的返回值的问题： function integer clog2( input logic[255:0] value);for(cl…...
微服务的初步使用
环境说明 jdk1.8 maven3.6.3 mysql8 idea2022 spring cloud2022.0.8 微服务案例的搭建 新建父工程 打开IDEA，File->New ->Project，填写Name（工程名称）和Location（工程存储位置），选…...
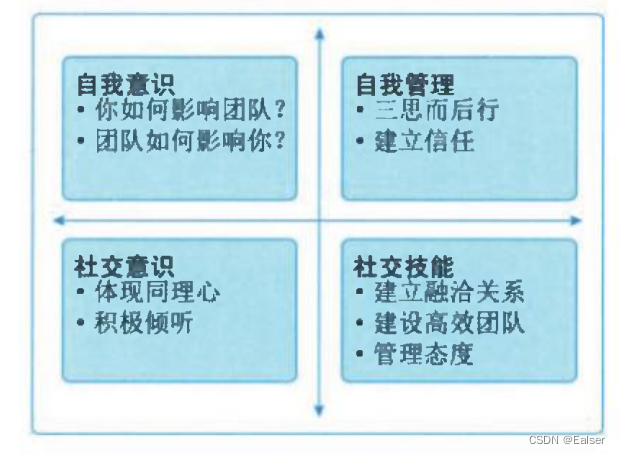
【2023年11月第四版教材】第18章《项目绩效域》(合集篇)
第18章《项目绩效域》（合集篇） 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相互…...
Android 11.0 mt6771新增分区功能实现三
1.前言 在11.0的系统开发中，在对某些特殊模块中关于数据的存储方面等需要新增分区来保存， 所以就需要在系统分区新增分区，接下来就来实现这个功能，看系列三的实现过程 2.mt6771新增分区功能实现三的核心类 build/make/tools/releasetools/common.py device/mediatek/mt6…...
计算机网络——计算机网络的性能指标（上）-速率、带宽、吞吐量、时延
目录 速率 比特 速率 例1 带宽 带宽在模拟信号系统中的意义 带宽在计算机网络中的意义 吞吐量 时延 发送时延 传播时延 处理时延 例2 例3 速率 了解速率之前，先详细了解一下比特： 比特 计算机中数据量的单位，也是信息论中信…...
每日一题 518零钱兑换2（完全背包）
题目 给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整…...
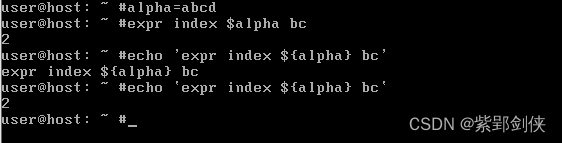
Linux shell编程学习笔记8：使用字符串
一、前言 字符串是大多数编程语言中最常用最有用的数据类型，这在Linux shell编程中也不例外。 本文讨论了Linux Shell编程中的字符串的三种定义方式的差别，以及字符串拼接、取字符串长度、提取字符串、查找子字符串等常用字符串操作,，以及反…...
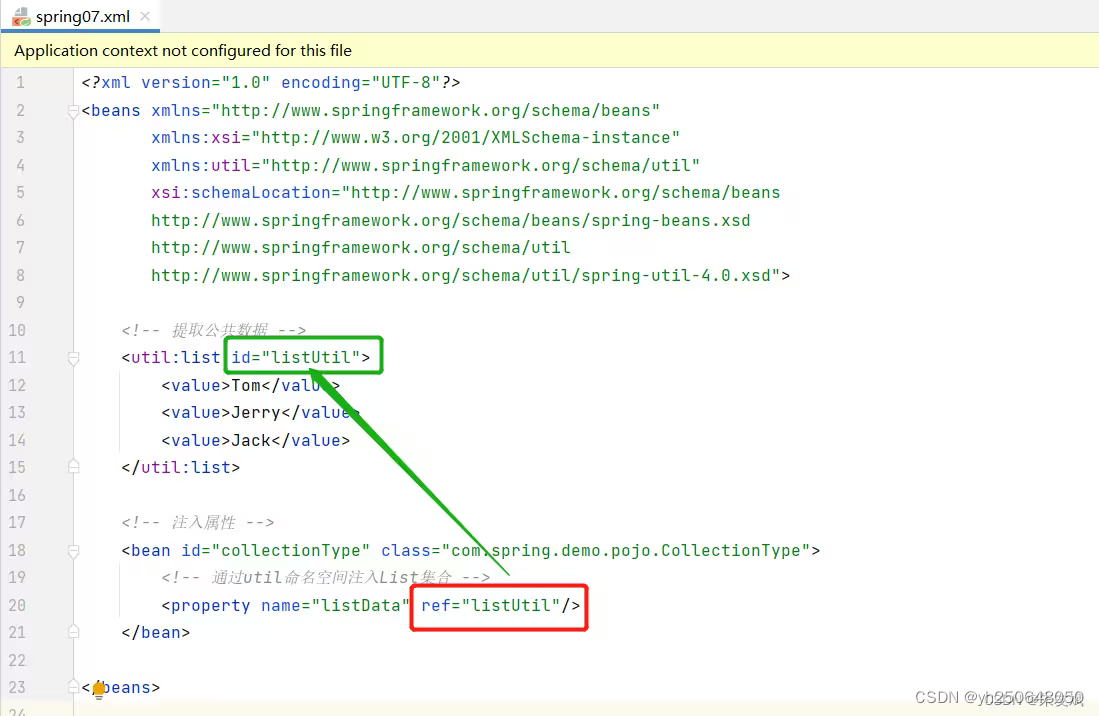
【Spring笔记03】Spring依赖注入各种数据类型
这篇文章，详细介绍一下Spring框架中如何注入各种数据类型，包含：注入基本数据类型、数组、集合、Map映射、Property属性、注入空字符串、注入null值、注入特殊字符等内容，以及如何使用命名空间进行依赖注入。 目录 一、注入各种数据…...
2023计算机保研——双非上岸酒吧舞
我大概是从22年10月份开始写博客的，当时因为本校专业的培养方案的原因，课程很多，有些知识纸质记录很不方便，于是选择了打破了自己的成见使用博客来记录学习生活。对于我个人而言，保研生活在前一大半过程中都比较艰难&a…...
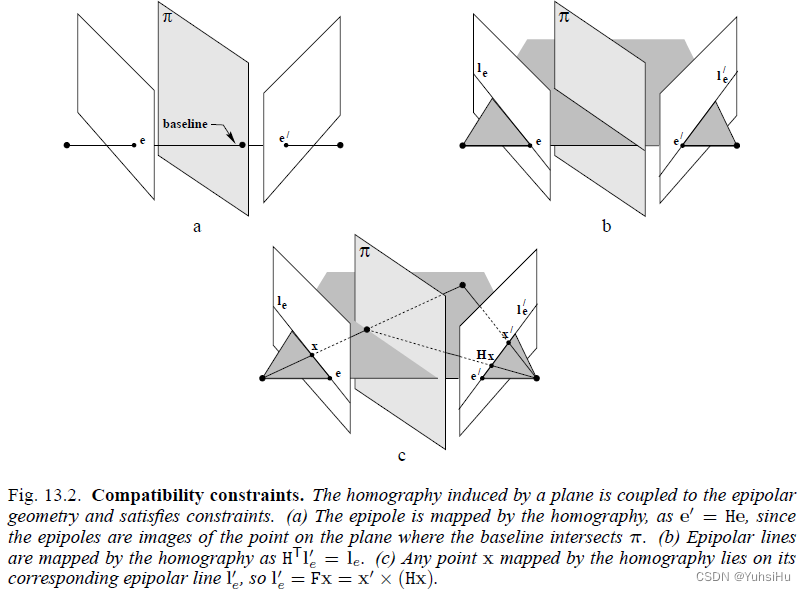
《计算机视觉中的多视图几何》笔记（13）
13 Scene planes and homographies 本章主要讲述两个摄像机和一个世界平面之间的射影几何关系。 我们假设空间有一平面 π \pi π，平面上的一点为 x π x_{\pi} xπ。 x π x_{\pi} xπ分别在两幅图像 P , P ′ P, P P,P′上形成了 x , x ′ x, x x,x′。 那…...
H5移动端购物商城系统源码 小型商城全新简洁风格全新UI 支持易支付接口
一款比较简单的 H5 移动端购物商城系统源码，比较适合单品商城、小型商城使用。带有易支付接口。 源码下载：https://download.csdn.net/download/m0_66047725/88391704 源码下载2：评论留言或私信留言...
全志ARM926 Melis2.0系统的开发指引⑤
全志ARM926 Melis2.0系统的开发指引⑤ 编写目的8. 固件修改工具(ImageModify)使用8.1.界面说明8.2.操作步骤8.2.1. 配置平台8.2.2. 选择固件8.2.3. 选择要替换的文件8.2.4. 替换文件8.2.5. 保存固件 8.3.注意事项8.4.增加固件修改权限设置8.4.1. 概述8.4.2. 操作说明8.4.2.1.打…...
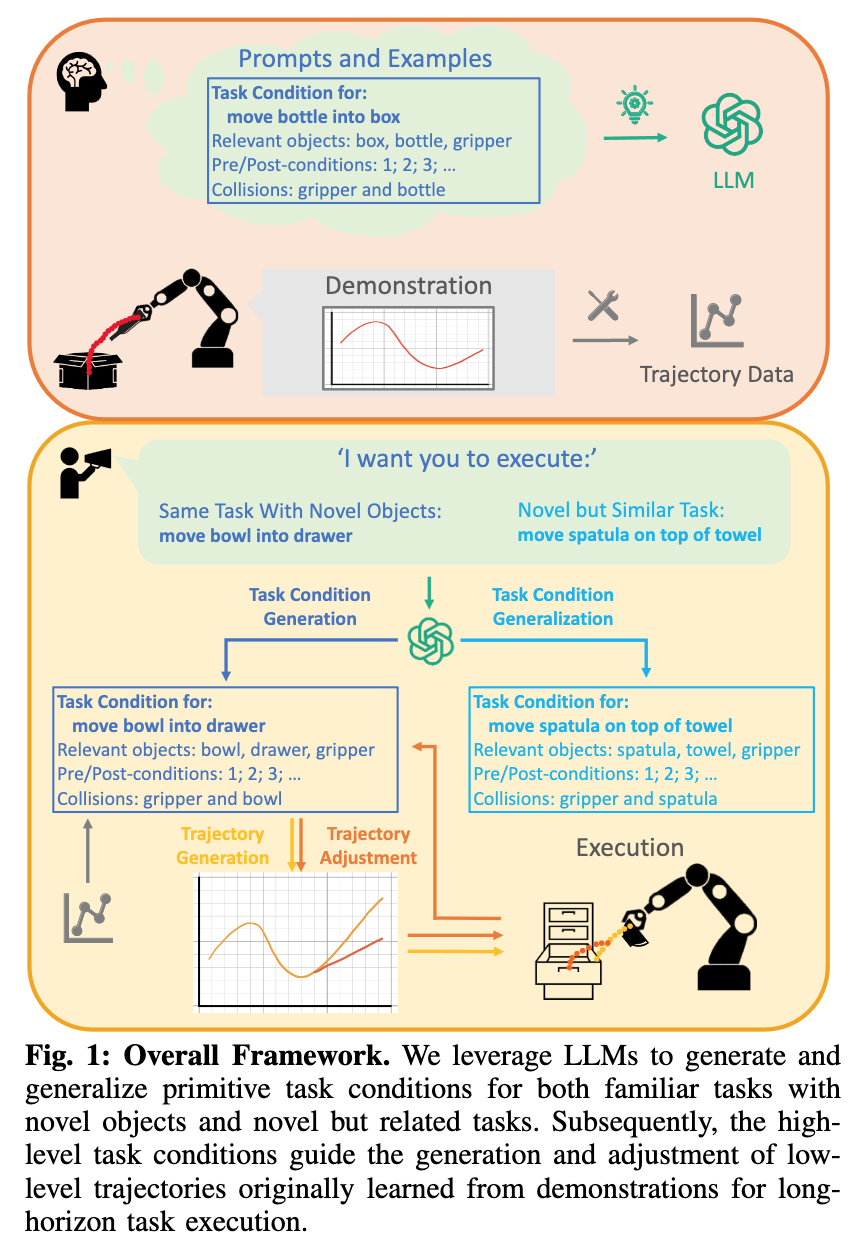
【AI视野·今日Robot 机器人论文速览 第四十七期】Wed, 4 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Wed, 4 Oct 2023 Totally 40 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚基于神经网络的多模态触觉感知, classification, position, posture, and force of the grasped object多模态形象的解耦(f…...
GPX可视化工具 GPX航迹预览工具
背景 当我们收到别人分享的航迹文档，即gpx文档时，如何快速的进行浏览呢？我们可以使用GIS软件来打开gpx文档并显示gpx中所记录的航迹，例如常用的GIS软件有googleEarth， Basecamp， GPXsee， GPX E…...
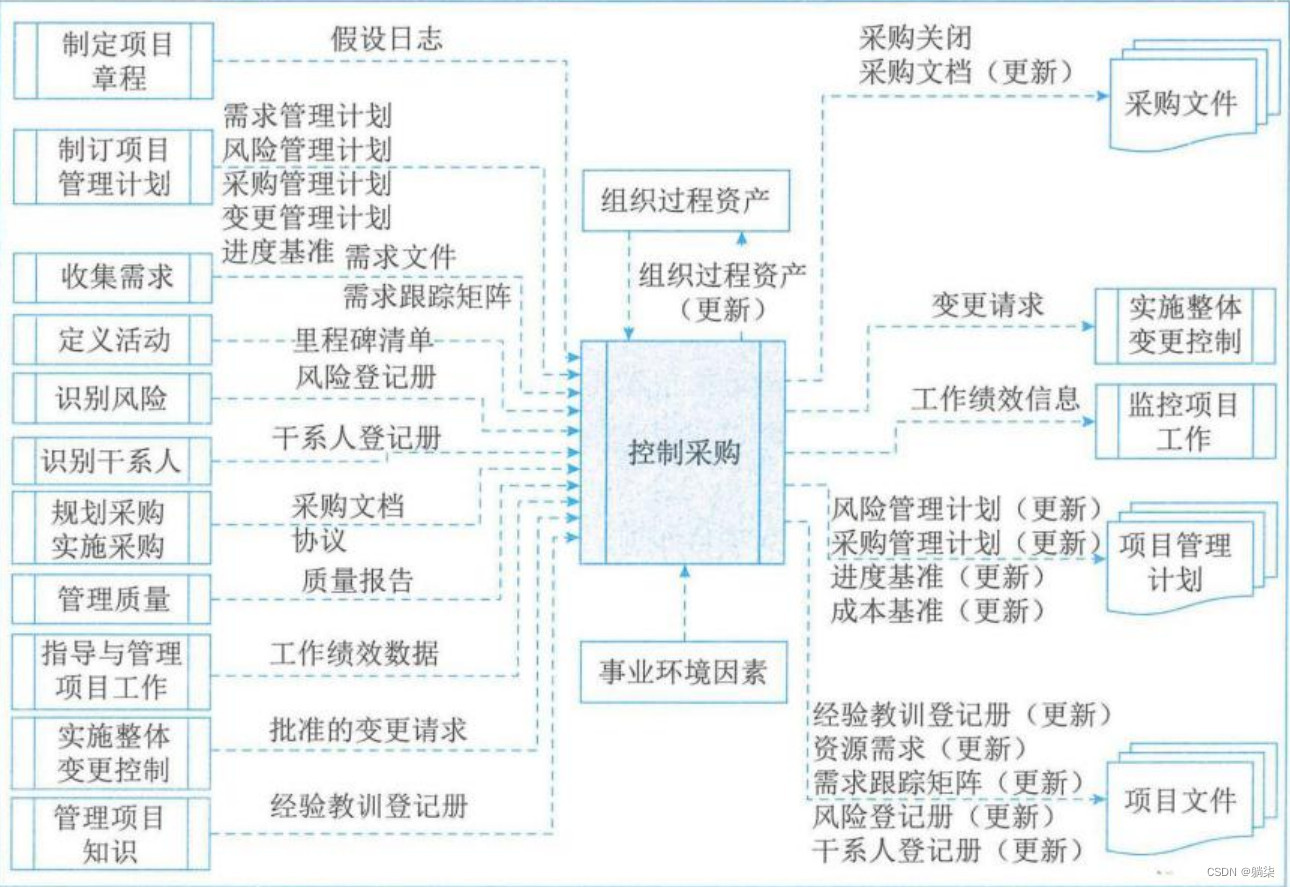
学信息系统项目管理师第4版系列18_采购管理
1. 协议 1.1. 合同 1.1.1. 国际合作的项目经理应牢记，无论合同规定如何详尽，文化和当地法律对合同及其可执行性均有影响 1.2. 服务水平协议（SLA） 1.3. 谅解备忘录 1.4. 协议备忘录（MOA） 1.5. 订购单 …...
标准化数据模型
标准化数据模型 标准化被定义为减少或消除数据集中冗余的过程。 它已成为关系数据库中数据建模的事实上的方法，很大程度上是由于这些系统最初设计时所围绕的底层资源限制：缓慢的磁盘和昂贵的 RAM。更少的数据冗余/重复意味着更有效地从磁盘读取数据并占…...
linux平台源码编译ffmpeg
目录 编译平台 编译步骤 编译平台 中标麒麟 编译步骤 1 从Download FFmpeg 下载源码，我选中了4.2.9版 2 解压 3 在解压后的目录下输入 ./configure --enable-shared --prefix/usr/local/ffmpeg 4 make 5 sudo make install 6 ffmpeg的头文件、可执行程…...
XML Group端口详解
在XML数据映射过程中，经常需要对数据进行分组聚合操作。例如，当处理包含多个物料明细的XML文件时，可能需要将相同物料号的明细归为一组，或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码，增加了开…...
生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式，可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
【kafka】Golang实现分布式Masscan任务调度系统
要求： 输出两个程序，一个命令行程序（命令行参数用flag）和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽，然后将消息推送到kafka里面。 服务端程序： 从kafka消费者接收…...
MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...
STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 （一）多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如，当用户上传一张“蓝色连衣裙”的图片时，接口可自动提取图像中的颜色（RGB值&…...
Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的，比GNOME简单得多！ 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库，例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体，比如 SnowballFight、Huggy the Do…...