高等数学笔记(下下)
无穷级数
定义
一般的,如果给定一个数列u1,u2,u3,...un,...,u_1, u_2, u_3, ... u_n, ... ,u1,u2,u3,...un,...,,那么由这个梳理构成的表达式u1+u2+u3+...+un+...u_1+u_2+u_3+...+u_n+...u1+u2+u3+...+un+...叫做(常数项)无穷级数,简称(常数项)级数,记作∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui,其中第n项叫做级数的一般项。取前n项求和,得到sn=∑i=1nuns_n=\sum\limits_{i=1}^nu_nsn=i=1∑nun,叫做级数的部分和。
如果级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui的部分和数列{sn}\{s_n\}{sn}有极限sss,称无穷级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui收敛,这时s叫做级数的和。如果{sn}\{s_n\}{sn}不收敛,则称无穷级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui发散。
当级数收敛时rn=s−snr_n=s-s_nrn=s−sn叫做级数的余项。
性质
- 性质1:如果级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui收敛于和s,那么级数∑i=1∞kui\sum\limits_{i=1}^{\infin}ku_ii=1∑∞kui收敛于ksksks.
证明:设∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui与∑i=1∞kui\sum\limits_{i=1}^{\infin}ku_ii=1∑∞kui的部分和分别是sns_nsn和σn\sigma_nσn,根据定义,有limn→∞sn=s\lim\limits_{n\to\infin}s_n=sn→∞limsn=s,σn=ku1+ku2+....=k(u1+u2+...)=ksn\sigma_n=ku_1+k_u2+....=k(u_1+u_2+...)=ks_nσn=ku1+ku2+....=k(u1+u2+...)=ksn,∴limn→∞∑i=1∞kui=ks\therefore \lim\limits_{n\to\infin}\sum\limits_{i=1}^{\infin}ku_i=ks∴n→∞limi=1∑∞kui=ks
推论:级数的每一项乘以一个不为零的常数(可以不同)之后,级数的收敛性不变。(证明可以通过定义和夹逼定理,取常数中的最大值和最小值进行逼近)。 - 性质2:如果级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui和∑i=1∞vi\sum\limits_{i=1}^{\infin}v_ii=1∑∞vi分别收敛于sss和σ\sigmaσ,则级数∑i=1∞(ui±vi)\sum\limits_{i=1}^{\infin}(u_i\pm v_i)i=1∑∞(ui±vi)收敛于s±σs\pm\sigmas±σ. 根据定义,结合极限的性质,容易证明。
- 性质3:在级数中增加、减少或者改变有限项,不会改变级数的收敛性。
- 性质4:如果级数收敛,那么对这个级数的任意项加括号之后组成的新级数,仍然收敛,且其和不变。(加括号之后收敛,之前不一定收敛,比如(1±1),(1±1))
- 性质5:级数收敛的必要条件:如果级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un收敛,那么它的一般项unu_nun趋于0.
证明:设级数的部分和为sns_nsn,则limn→∞sn=s\lim\limits_{n\to\infin}s_n=sn→∞limsn=s,limn→∞un=limn→∞sn−limn→∞sn−1=s−s=0\lim\limits_{n\to\infin}u_n=\lim\limits_{n\to\infin}s_n-\lim\limits_{n\to\infin}s_{n-1}=s-s=0n→∞limun=n→∞limsn−n→∞limsn−1=s−s=0
问题:讨论级数∑n=1∞un=∑n=1∞nα\sum\limits_{n=1}^{\infin}u_n=\sum\limits_{n=1}^{\infin}n^\alphan=1∑∞un=n=1∑∞nα何时收敛。
当α≥0\alpha\ge0α≥0,un>1u_n>1un>1,此时,部分和sns_nsn发散,此时级数必然发散。
当α<−1\alpha<-1α<−1,∣un+1+un+2+...un+p∣=∣(n+1)α+(n+2)α+...+(n+p)α∣<∣p(n+1)α∣|u_{n+1}+u_{n+2}+...u_{n+p}|=|(n+1)^\alpha+(n+2)^\alpha+...+(n+p)^\alpha|<|p(n+1)^\alpha|∣un+1+un+2+...un+p∣=∣(n+1)α+(n+2)α+...+(n+p)α∣<∣p(n+1)α∣,根据柯西审敛定理,对于任意小的正数ϵ\epsilonϵ,都有∣p(n+1)α∣<ϵ|p(n+1)^\alpha|<\epsilon∣p(n+1)α∣<ϵ,只需要n>(ϵp)1α−1n>(\frac{\epsilon}{p})^\frac{1}{\alpha}-1n>(pϵ)α1−1
当α=−1时\alpha=-1时α=−1时,级数发散;
当α∈(−1,0)\alpha \in(-1,0)α∈(−1,0),其每一项都比α=−1\alpha=-1α=−1时要大,故发散。
- 柯西审敛定理
级数∑i=1∞ui\sum\limits_{i=1}^{\infin}u_ii=1∑∞ui收敛的充分必要条件是对于任意给定的正整数ϵ\epsilonϵ,总存在正整数N,使得当n>Nn>Nn>N时,对于任意正整数p都有
∣∑i=1pun+i∣<ϵ|\sum_{i=1}^pu_{n+i}|<\epsilon∣i=1∑pun+i∣<ϵ
正项级数审敛法
- 定理1:正项级数∑n=1∞un\sum\limits_{n=1}^{\infin}u_nn=1∑∞un收敛的充分必要条件是,它的部分和数列{s_n}有界。注意是正项级数。
- 定理2:比较审敛法:
设级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un和∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn都是正项级数,且un≤vn(n=1,2,...)u_n\le v_n(n=1, 2,...)un≤vn(n=1,2,...),若级数∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn收敛,则级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un也收敛;若∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un发散,则∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn也发散。 - 定理3:比较审敛法的极限形式
设级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un和∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn都是正项级数,
(1)如果limn→∞unvn=l(0≤l<+∞)\lim\limits_{n\to\infin}\frac{u_n}{v_n}=l(0\le l<+\infin)n→∞limvnun=l(0≤l<+∞),且级数∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn收敛,那么级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un也收敛;
(2)如果limn→∞unvn=l(l>0)\lim\limits_{n\to\infin}\frac{u_n}{v_n}=l(l>0)n→∞limvnun=l(l>0),且级数∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn发散,那么级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un也发散;
这个定理的一个直观理解是,如果对于级数的每一项,unu_nun和vnv_nvn是同阶或者更高阶,无穷小。∑i=n∞vn收敛⟹∑i=n∞un收敛\sum\limits_{i=n}^{\infin}v_n收敛\implies \sum\limits_{i=n}^{\infin}u_n收敛i=n∑∞vn收敛⟹i=n∑∞un收敛 - 定理4:比值审敛法,达朗贝尔判别法:设级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un是正项级数,如果
limn→∞unun−1=ρ\lim\limits_{n\to\infin}\frac{u_n}{u_{n-1}}=\rhon→∞limun−1un=ρ,当ρ<1\rho<1ρ<1时,级数收敛;当ρ>1\rho>1ρ>1时,级数发散;当ρ=1\rho=1ρ=1时,级数可能收敛也可能发散;
这个定理的一个直观理解,如果当n→∞n\to\infinn→∞时,unu_nun趋于等比数列,则其收敛性和等比数列类似。 - 定理5:根式审敛法,柯西判别法
设级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un为正项级数,如果limn→∞unn=ρ\lim\limits_{n\to\infin}\sqrt[n]{u_n}=\rhon→∞limnun=ρ,当ρ<1\rho<1ρ<1时,级数收敛;当ρ>1\rho>1ρ>1时,级数发散;当ρ=1\rho=1ρ=1时,级数可能收敛也可能发散;
证明:因为limn→∞unn=ρ\lim\limits_{n\to\infin}\sqrt[n]{u_n}=\rhon→∞limnun=ρ,设当n>N时,对于任意n都有unn<ρ+ϵ<1\sqrt[n]{u_n}<\rho+\epsilon<1nun<ρ+ϵ<1,所以,当n>N时,总有un<(ρ+ϵ)nu_n<(\rho+\epsilon)^nun<(ρ+ϵ)n,后者是个公比为ρ+ϵ\rho+\epsilonρ+ϵ的等比数列,公比小于1,根据比较审敛法,级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un收敛。 - 定理6:极限审敛法:
若级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un为正项级数,
(1)若limn→∞nun=l(l>0)\lim\limits_{n\to\infin}nu_n=l(l>0)n→∞limnun=l(l>0),则级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un发散;
(2)若limn→∞npun=l(l∈[0,∞),p>1)\lim\limits_{n\to\infin}n^pu_n=l(l\in[0,\infin), p>1)n→∞limnpun=l(l∈[0,∞),p>1),则级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un收敛;
说明unu_nun是1np\frac{1}{n^p}np1的同阶无穷小,具有相同的收敛性;
交错级数审敛法
交错级数:各项是正负相间的。
- 定理7:莱布尼茨定理
若交错级数∑i=n∞(−1)n−1un\sum\limits_{i=n}^{\infin}(-1)^{n-1}u_ni=n∑∞(−1)n−1un满足条件
(1) un≥un+1(n=1,2,3,...)u_n\ge u{n+1} (n=1,2,3,...)un≥un+1(n=1,2,3,...),
(2)limn→∞un=0\lim\limits_{n\to\infin}u_n=0n→∞limun=0,
那么级数收敛,且其和小于sn≤u1s_n\le u_1sn≤u1,余项∣rn∣≤un+1|r_n|\le u_{n+1}∣rn∣≤un+1
绝对收敛与条件收敛:
若级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un各项绝对值构成的级数∑i=n∞∣un∣\sum\limits_{i=n}^{\infin}|u_n|i=n∑∞∣un∣收敛,则成为绝对收敛,∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un收敛而∑i=n∞∣un∣\sum\limits_{i=n}^{\infin}|u_n|i=n∑∞∣un∣不收敛,称为条件收敛。 - 定理10:绝对收敛级数的乘法:
设级数∑i=n∞un\sum\limits_{i=n}^{\infin}u_ni=n∑∞un和∑i=n∞vn\sum\limits_{i=n}^{\infin}v_ni=n∑∞vn都绝对收敛,其和分别为sss和σ\sigmaσ,则他们的柯西乘积u1v1+(u1v2+u2v1)+...∑i=1nu1vn−1+...u_1v_1+(u_1v_2+u_2v_1)+...\sum\limits_{i=1}^{n}u_1v_{n-1}+...u1v1+(u1v2+u2v1)+...i=1∑nu1vn−1+...也绝对收敛,其和为sσs\sigmasσ.
幂级数
如果给定一个在区间I上的函数列,u1(x),u2(x),...,un(x),...u_1(x), u_2(x), ... , u_n(x), ...u1(x),u2(x),...,un(x),...,那么由这个函数列构成的表达式f(x)=u1(x)+u2(x)+...+un(x)+...f(x)=u_1(x)+u_2(x)+... +u_n(x)+...f(x)=u1(x)+u2(x)+...+un(x)+...,称为定义在区间I上的(函数项)无穷级数,简称(函数项)级数。对于每个确定的值x0∈Ix_0\in Ix0∈I,级数f(x0)f(x_0)f(x0)可能收敛也可能发散,如果收敛,就称x0x_0x0是级数的收敛点,否则称为发散点,收敛点的全体称为收敛域,发散点的全体,称为发散域。对于收敛域内的一点x,函数项级数称为一个收敛的常数项级数,因而有一组确定的和s,这样在收敛域上,函数项级数的和是x的函数s(x)s(x)s(x),通常称为函数项级数的和函数。
幂级数及其收敛性
幂级数:函数项级数中常见的一类是每一项都是常数和幂函数相乘的形式,即所谓幂级数,它的形式是
∑n=0∞anxn=a0+a1x+a2x2+...+anxn+...\sum_{n=0}^{\infin}a_nx^n=a_0+a_1x+a_2x^2+...+a_nx^n+...n=0∑∞anxn=a0+a1x+a2x2+...+anxn+...
- 定理1:阿贝尔定理:
如果级数∑n=0∞anxn\sum\limits_{n=0}^{\infin}a_nx^nn=0∑∞anxn在x0(x0≠0)x_0(x_0\ne0)x0(x0=0)收敛,则对于所有∣x∣<∣x0∣|x|<|x_0|∣x∣<∣x0∣的所有点,都收敛。反之,如果级数在x0x_0x0处发散,对于所有∣x∣>∣x0∣|x|>|x_0|∣x∣>∣x0∣,级数都发散。 - 定理2:如果limn→∞∣an+1an∣=ρ\lim\limits_{n\to\infin}\left|\frac{a_{n+1}}{a_n}\right|=\rhon→∞limanan+1=ρ其中an,an+1a_{n}, a_{n+1}an,an+1是相邻两项的系数,则级数收敛域:
R={1ρρ≠0+∞ρ=00ρ=+∞R= \begin{cases} \begin{aligned} &\frac{1}{\rho} \space\space&\rho\ne0\\ &+\infin&\rho=0\\ &0&\rho=+\infin\\ \end{aligned} \end{cases} R=⎩⎨⎧ρ1 +∞0ρ=0ρ=0ρ=+∞
问题:在收敛域内的意义是明确的,可以使用无穷级数来逼近和函数。如果不在收敛域内,则完全不能逼近?如果是个低阶无穷大,有意义吗?
幂级数运算的性质
幂级数∑n=0∞anxn\sum\limits_{n=0}^{\infin}a_nx^nn=0∑∞anxn和∑n=0∞bnxn\sum\limits_{n=0}^{\infin}b_nx^nn=0∑∞bnxn分别在区间(−R,R)(-R,R)(−R,R)和(−R′,R′)(-R',R')(−R′,R′)上收敛,则二者加和、差、柯西乘积都收敛,收敛域取两者较小的集合。但是两者相除可能会比原来的收敛域小的多。
- 性质1:幂级数∑n=0∞anxn\sum\limits_{n=0}^{\infin}a_nx^nn=0∑∞anxn在其收敛域I上连续。
- 性质2: 幂级数∑n=0∞anxn\sum\limits_{n=0}^{\infin}a_nx^nn=0∑∞anxn在其收敛域I上可积,并有逐项积分公式:
∫0xs(t)dt=∫0x[∑0∞antn]dt=∑0∞∫0xantndt=∑0∞ann+1xn+1(x∈I)\begin{aligned} \int_0^xs(t)dt&=\int_0^x[\sum_0^\infin a_nt^n]dt\\ &=\sum_0^\infin\int_0^xa_nt^ndt\\ &=\sum_0^\infin\frac{a_n}{n+1}x^{n+1}\space(x\in I) \end{aligned} ∫0xs(t)dt=∫0x[0∑∞antn]dt=0∑∞∫0xantndt=0∑∞n+1anxn+1 (x∈I)
逐项积分后所得幂级数和原级数具有相同的收敛半径。 - 性质3:幂级数∑n=0∞anxn\sum\limits_{n=0}^{\infin}a_nx^nn=0∑∞anxn在其收敛区间(−R,R)(-R,R)(−R,R)逐项可导,且有逐项求导公式,
s′(x)=(∑n=0∞anxn)′=∑n=0∞nanxn−1(∣x∣<R)s'(x)=\left(\sum_{n=0}^\infin a_nx^n\right)'=\sum_{n=0}^\infin na_nx^{n-1}(|x|<R)s′(x)=(n=0∑∞anxn)′=n=0∑∞nanxn−1(∣x∣<R) - 看性质2和性质3,常数项里不是多了个n吗?(一个是1/(n+1),一个n)为什么还会说收敛半径不变呢?参照定理2,看逐项积分的情况。逐项积分后的级数为∑n=0∞nanxn−1\sum\limits_{n=0}^\infin na_nx^{n-1}n=0∑∞nanxn−1,其常数项bn=ann+1b_n=\frac{a_n}{n+1}bn=n+1an,limn→∞∣bn+1bn∣=limn→∞∣an+1an⋅nn+1∣=limn→∞∣an+1an∣=ρ\lim\limits_{n\to\infin}\left|\frac{b_{n+1}}{b_n}\right|=\lim\limits_{n\to\infin}\left|\frac{a_{n+1}}{a_n}\cdot\frac{n}{n+1}\right|=\lim\limits_{n\to\infin}\left|\frac{a_{n+1}}{a_n}\right|=\rhon→∞limbnbn+1=n→∞limanan+1⋅n+1n=n→∞limanan+1=ρ故两者具有相同的收敛半径。
常数项级数如果单项乘以n或者除以n就有可能会导致收敛性改变,为什么函数项级数不会有这个问题?例如对于常数项级数∑n∞un=∑n∞1n2\sum\limits_{n}^\infin u_n=\sum\limits_{n}^\infin\frac1{n^2}n∑∞un=n∑∞n21是收敛的,但是∑n∞unn=∑n∞1n\sum\limits_{n}^\infin u_nn=\sum\limits_{n}^\infin\frac 1{n}n∑∞unn=n∑∞n1发散,但是∑n∞un(x)=∑n∞xn2\sum\limits_{n}^\infin u_n(x)=\sum\limits_{n}^\infin\frac x{n^2}n∑∞un(x)=n∑∞n2x收敛域是[−1,1][-1,1][−1,1],∑n∞un(x)n=∑n∞nxn2\sum\limits_{n}^\infin u_n(x)n=\sum\limits_{n}^\infin\frac {nx}{n^2}n∑∞un(x)n=n∑∞n2nx收敛域是[-1,1),收敛半径看似没变,只是少了一个收敛点。乘以多项式是不会改变收敛半径的,增加什么样的n的变量会改变x的收敛半径呢?也容易看到,比如ana^nan,会把收敛域变成原来的1/a1/a1/a.
函数展开成幂级数
假设f(x)f(x)f(x)能展开成如下幂级数形式
f(x)=∑n=0∞an(x−x0)=a0+a1(x−x0)+a2(x−x0)2+...+...f(x)=\sum_{n=0}^\infin a_n(x-x_0)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+...+...f(x)=n=0∑∞an(x−x0)=a0+a1(x−x0)+a2(x−x0)2+...+...
则有f(x)f(x)f(x)在U(x0)U(x_0)U(x0)内具有任意阶导数,且
f(n)(x)=n!an+∑k=n+1∞k!(k−n)!ak(x−x0)k−nf^{(n)}(x)=n!a_n+\sum_{k=n+1}^\infin\frac{k!}{(k-n)!}a_k(x-x_0)^{k-n}f(n)(x)=n!an+k=n+1∑∞(k−n)!k!ak(x−x0)k−n
在x=x0x=x_0x=x0处,后面的求和项为0, 故an=f(n)(x0)n!a_n=\frac{f^{(n)}(x_0)}{n!}an=n!f(n)(x0)
这叫做函数f(x)f(x)f(x)在x0x_0x0处的泰勒级数。
傅里叶级数
如何研究非正弦周期函数呢?,可以将周期为T=2π/ωT=2\pi/\omegaT=2π/ω的周期函数用一系列以T为周期的正弦函数来表示,记作
f(t)=A0+∑n=1∞Ansin(nωt+φn)f(t)=A_0+\sum_{n=1}^\infin A_n sin(n\omega t+\varphi_n)f(t)=A0+n=1∑∞Ansin(nωt+φn)
可以再做变形得到,
f(t)=A0+∑n=1∞Ansin(nωt)cosφ+Ancos(nωt)sinφf(t)=A_0+\sum_{n=1}^\infin A_n sin(n\omega t)cos\varphi+A_n cos(n\omega t)sin\varphif(t)=A0+n=1∑∞Ansin(nωt)cosφ+Ancos(nωt)sinφ
进行变量替换
a02=A0,an=Ansinφ,bn=Ancosφ,2π2l=ω(T=2l)\frac{a_0}{2}=A_0, a_n=A_nsin\varphi, b_n=A_ncos\varphi, \frac{2\pi}{2l}=\omega(T=2l)2a0=A0,an=Ansinφ,bn=Ancosφ,2l2π=ω(T=2l)
得到
f(t)=a02+∑n=1∞ancos(nπtl)+bnsin(nπtl)f(t)=\frac{a_0}{2}+\sum_{n=1}^\infin a_n cos(\frac{n\pi t}{l})+b_n sin(\frac{n\pi t}{l})f(t)=2a0+n=1∑∞ancos(lnπt)+bnsin(lnπt)
令
x=πtlx=\frac{\pi t}{l}x=lπt
这样就把以2l为周期的函数变换成了以2π2\pi2π为周期的函数,研究起来方便。当然,研究2l2l2l为周期的函数也是没有问题的。
- 三角函数的正交性:三角函数系在[−l,l][-l, l][−l,l]上正交(即任意两个不同三角函数乘积的积分为0),其中2l(l=π/ω)2l(l=\pi/\omega)2l(l=π/ω)是基波周期。
如1,sinωx,coskωx....1, sin\omega x,cosk\omega x....1,sinωx,coskωx....
举个例子:
s=∫−llsinpωtsinqωtdt=∫−llcos(p−q)ωt−sin(p+q)ωtdt若p≠q,则有s=1(p−q)ωsin(p−q)ωt∣−ll+1(p+q)ωcos(p+q)ωt∣−ll=0若p=q,则有s=∫−lldt=2l\begin{aligned} &s=\int_{-l}^l \sin p\omega t\sin q\omega t dt\\ =&\int_{-l}^l \cos (p-q)\omega t-\sin(p+q)\omega t dt \\ \end{aligned}\\ 若p\ne q,则有\\ s = \left.\frac{1}{(p-q)\omega}\sin (p-q)\omega t \right|_{-l}^{l} +\left.\frac{1}{(p+q)\omega}\cos (p+q)\omega t \right|_{-l}^{l} = 0 若p=q,则有\\ s = \int_{-l}^ldt=2l =s=∫−llsinpωtsinqωtdt∫−llcos(p−q)ωt−sin(p+q)ωtdt若p=q,则有s=(p−q)ω1sin(p−q)ωt−ll+(p+q)ω1cos(p+q)ωt−ll=0若p=q,则有s=∫−lldt=2l - 函数展开成傅里叶级数
设f(x)f(x)f(x)是以2π2\pi2π为周期的函数,且能展开成三角函数
f(x)=a02+∑n=1∞ancosnx+bnsinnxf(x)=\frac{a_0}{2}+\sum_{n=1}^\infin a_n\cos n x+b_n \sin nxf(x)=2a0+n=1∑∞ancosnx+bnsinnx那么改怎么求取各个系数呢?
先求a0a_0a0,两边同时在[−π,π][-\pi, \pi][−π,π]上积分得到
∫−ππf(x)dx=∫−ππa02dx+∫−ππ∑n=1∞(ancosnx+bnsinnx)dx\int_{-\pi}^{\pi}f(x)dx=\int_{-\pi}^{\pi} \frac{a_0}{2}dx+\int_{-\pi}^{\pi}\sum_{n=1}^\infin (a_n\cos n x+b_n \sin nx)dx∫−ππf(x)dx=∫−ππ2a0dx+∫−ππn=1∑∞(ancosnx+bnsinnx)dx根据三角函数的正交性可知,等式右边积分的第二项为0,故
a0=1π∫−ππf(x)dxa_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dxa0=π1∫−ππf(x)dx
为了求取ana_nan,等式两边同时乘以cosnx\cos nxcosnx,并在[−π,π][-\pi, \pi][−π,π]上进行积分,得到
∫−ππf(x)cosnxdx=∫−ππa02cosnxdx+∫−ππ∑n=1∞(ancosnx+bnsinnx)cosnxdx=∫−ππancos2nxdx=∫−ππan2dx=πan⟹an=1π∫−ππf(x)cosnxdx同理,bn=1π∫−ππf(x)sinnxdx\begin{aligned} &\int_{-\pi}^{\pi}f(x)\cos nxdx\\ =&\int_{-\pi}^{\pi} \frac{a_0}{2}\cos nxdx +\int_{-\pi}^{\pi}\sum_{n=1}^\infin (a_n\cos n x+b_n \sin nx)\cos nxdx\\ =&\int_{-\pi}^{\pi}a_n \cos^2 nxdx\\ =&\int_{-\pi}^{\pi}\frac{a_n}{2}dx\\ =&\pi a_n\\ \implies a_n=&\frac 1{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx\\ 同理, b_n=&\frac 1{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\\ \end{aligned}\\ ====⟹an=同理,bn=∫−ππf(x)cosnxdx∫−ππ2a0cosnxdx+∫−ππn=1∑∞(ancosnx+bnsinnx)cosnxdx∫−ππancos2nxdx∫−ππ2andxπanπ1∫−ππf(x)cosnxdxπ1∫−ππf(x)sinnxdx - 三角级数收敛定理(狄利克雷充分条件):
设f(x)f(x)f(x)是周期为2π2\pi2π的周期函数,如果它满足:
(1)在一个周期内连续,或者只有有限个第一类间断点;
(2)在一个周期内至多只有有限个极值点;
那么f(x)的傅里叶级数收敛,并且:
当x是f(x)f(x)f(x)的连续点时,级数收敛于f(x)f(x)f(x);
当x是f(x)f(x)f(x)的间断点时,级数收敛于1/2(f(x−)+f(x+))1/2(f(x^-)+f(x^+))1/2(f(x−)+f(x+)) - 一般周期函数的傅里叶级数
设一般周期函数具有周期T=2lT=2lT=2l,则可以写成傅里叶级数
f(x)=a02+∑n=1∞ancosnπlx+bnsinnπlxan=1l∫−llf(x)cosnπlxdxbn=1l∫−llf(x)sinnπlxdxf(x)=\frac{a_0}{2}+\sum_{n=1}^\infin a_n\cos \frac{n\pi}{l}x+b_n\sin \frac{n\pi}{l}x\\ a_n=\frac 1 l \int_{-l}^{l}f(x)\cos \frac{n\pi}{l}xdx\\ b_n=\frac 1 l \int_{-l}^{l}f(x)\sin \frac{n\pi}{l}xdx f(x)=2a0+n=1∑∞ancoslnπx+bnsinlnπxan=l1∫−llf(x)coslnπxdxbn=l1∫−llf(x)sinlnπxdx - 傅里叶级数的复数形式
周期为2l2l2l的函数的傅里叶变换
f(x)=a02+∑n=1∞ancosnπlx+bnsinnπlxf(x)=\frac{a_0}{2}+\sum_{n=1}^\infin a_n\cos \frac{n\pi}{l}x+b_n\sin \frac{n\pi}{l}x\\ f(x)=2a0+n=1∑∞ancoslnπx+bnsinlnπx
根据欧拉公式
cosx=exi+e−xi2,sinx=−exi−e−xi2i\cos x = \frac{e^{xi}+e^{-xi}}{2}, \sin x=-\frac{e^{xi}-e^{-xi}}{2}i cosx=2exi+e−xi,sinx=−2exi−e−xii
带入上式得到
f(x)=a02+∑n=1∞an−bni2enπxil+an+bni2e−nπxilf(x)=\frac{a_0}{2}+\sum_{n=1}^\infin \frac{a_n-b_ni}{2}e^{\frac{n\pi xi}{l}}+ \frac{a_n+b_ni}{2}e^{-\frac{n\pi xi}{l}} f(x)=2a0+n=1∑∞2an−bnielnπxi+2an+bnie−lnπxi
令cn=an−bni2,dn=an+bni2c_n= \frac{a_n-b_ni}{2}, d_n= \frac{a_n+b_ni}{2}cn=2an−bni,dn=2an+bni,则对两边同时乘一个量,同时做积分,根据虚指数函数的正交性
∫−llf(x)e−nπxildx=∫−lla02e−nπxildx+∫−ll(∑n=1∞an−bni2enπxil+an+bni2e−nπxil)e−nπxildx=∫−llcndx=2lcn⟹cn=12l∫−llf(x)e−nπxildx类似dn=12l∫−llf(x)e−nπxildx合并可得f(x)=∑−∞∞cnenπxil其中cn=∫−llf(x)e−nπxildx\begin{aligned} &\int_{-l}^lf(x)e^{-\frac{n\pi xi}{l}}dx\\ =&\int_{-l}^l\frac{a_0}{2}e^{-\frac{n\pi xi}{l}}dx +\int_{-l}^l\left(\sum_{n=1}^\infin \frac{a_n-b_ni}{2}e^{\frac{n\pi xi}{l}} +\frac{a_n+b_ni}{2}e^{-\frac{n\pi xi}{l}}\right)e^{-\frac{n\pi xi}{l}}dx\\ =&\int_{-l}^{l}c_ndx\\ =&2lc_n\\ \implies c_n=&\frac{1}{2l}{\int_{-l}^lf(x)e^{-\frac{n\pi xi}{l}}dx}\\ 类似d_n=&\frac{1}{2l}{\int_{-l}^lf(x)e^{-\frac{n\pi xi}{l}}dx}\\ 合并可得\\ f(x)=\sum_{-\infin}^{\infin}c_ne^\frac{n\pi xi}{l}\\ 其中c_n=\int_{-l}^lf(x)e^{-\frac{n\pi xi}{l}}dx \end{aligned}\\ ===⟹cn=类似dn=合并可得f(x)=−∞∑∞cnelnπxi其中cn=∫−llf(x)e−lnπxidx∫−llf(x)e−lnπxidx∫−ll2a0e−lnπxidx+∫−ll(n=1∑∞2an−bnielnπxi+2an+bnie−lnπxi)e−lnπxidx∫−llcndx2lcn2l1∫−llf(x)e−lnπxidx2l1∫−llf(x)e−lnπxidx
能不能直接通过指数表达式展开成指数形式,而不通过三角级数间接转换?
相关文章:
)
高等数学笔记(下下)
无穷级数 定义 一般的,如果给定一个数列u1,u2,u3,...un,...,u_1, u_2, u_3, ... u_n, ... ,u1,u2,u3,...un,...,,那么由这个梳理构成的表达式u1u2u3...un...u_1u_2u_3...u_n...u1u2u3...un...叫做(常数项)无穷级数,简称(常…...
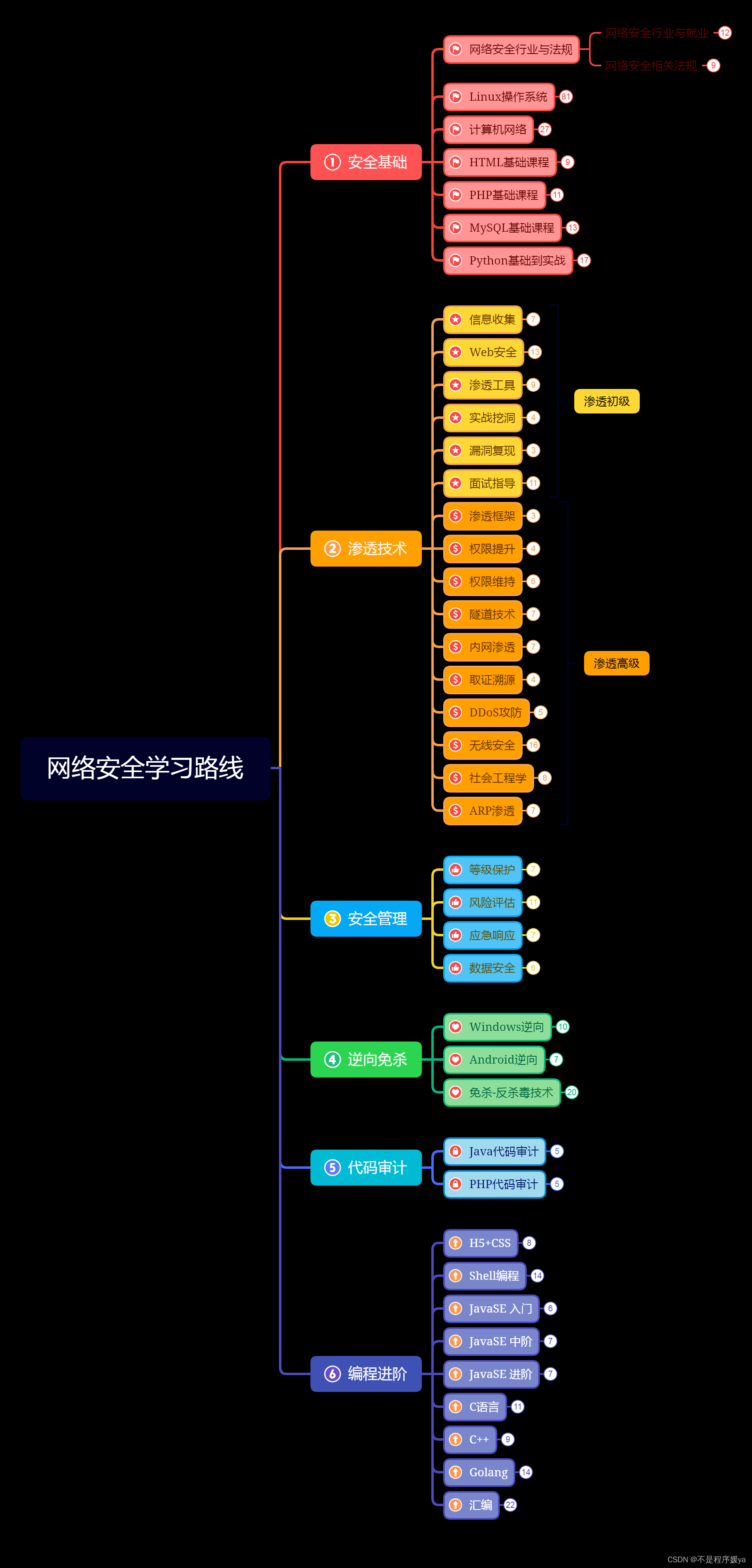
零基础如何入门网络安全(黑客)
我经常会看到这一类的问题: 学习XXX知识没效果;学习XXX技能没方向;学习XXX没办法入门; 给大家一个忠告,如果你完全没有基础的话,前期最好不要盲目去找资料学习,因为大部分人把资料收集好之后&a…...

【C++】map和set用法详解
文章目录1.关联式容器2.键值对3.树形结构的关联式容器3.1 set3.1.1 set的介绍3.1.2 set的模板参数列表3.1.3 set的使用3.2 mapmap的介绍map的模板参数列表map的使用关于map的元素访问总结3.3multimap1.关联式容器 我们接触过STL中的部分容器,比如:vecto…...

BLIP2-图像文本预训练
文章目录摘要解决问题算法模型结构通过frozen图像编码器学习视觉语言表征图像文本对比学习(ITC)基于图像文本生成(ITG)图文匹配(ITM)从大规模语言模型学习视觉到语言生成模型预训练预训练数据预训练图像编码…...
Faster-Rcnn修改转数据集文件
目录 学习python的一些基础知识 argparser assert关键字 让你秒懂Python 类特殊方法__getitem__ lxml.etree.fromstring的使用 统计一下json文件内的种类 正脸红外光 正脸-混合红外光 正脸-交叉偏振光 正脸-平行偏振光 正脸-紫外光 正脸-棕色光 调用mydataset可视化…...
带你沉浸式体验删库跑路
前言:学习的过程比较枯燥,后面会记录一些比较有意思的东西,比如程序员之间流传的删库跑路的梗,当然本次测试是在虚拟机上进行的并进行了快照保护,所以其实没太大问题。首先得要有一个虚拟机要有一个linux iso文件装在虚拟机上以上两点不是本文重点,如果有需要可以私…...
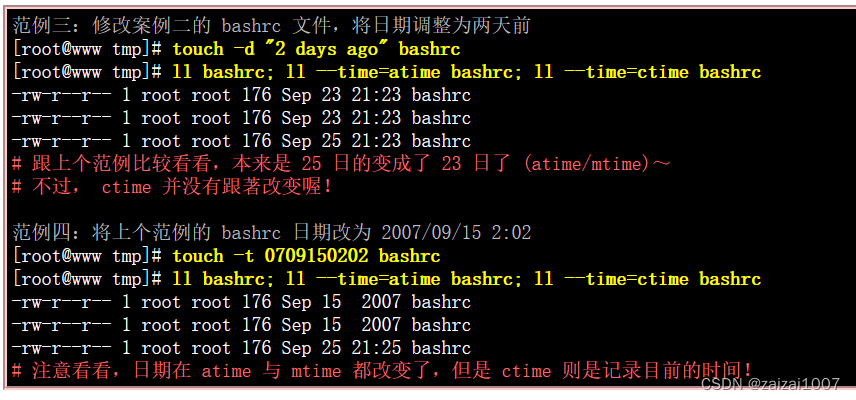
Linux学习(8.5)文件内容查阅
目录 文件内容查阅: 直接检视文件内容 cat (concatenate) tac (反向列示) nl (添加行号列印) 可翻页检视 more (一页一页翻动) less (一页一页翻动) 数据撷取 tail (取出后面几行) 非纯文字档: od 修改文件时间或建置新档: touc…...
【Docker】命令总结
目录 1.镜像命令 1.1拉取镜像 1.2查看镜像 1.3保存镜像 1.4导入镜像 2.容器命令 2.1创建并运行容器 2.2删除容器 2.3进入容器 2.4查看容器状态 2.5暂停容器 2.6恢复容器 2.7停止容器 2.8启动容器 2.8查看容器日志 3.数据卷命令 3.1创建数据卷 3.2查看所有数据…...
并发编程-学习总结(上)
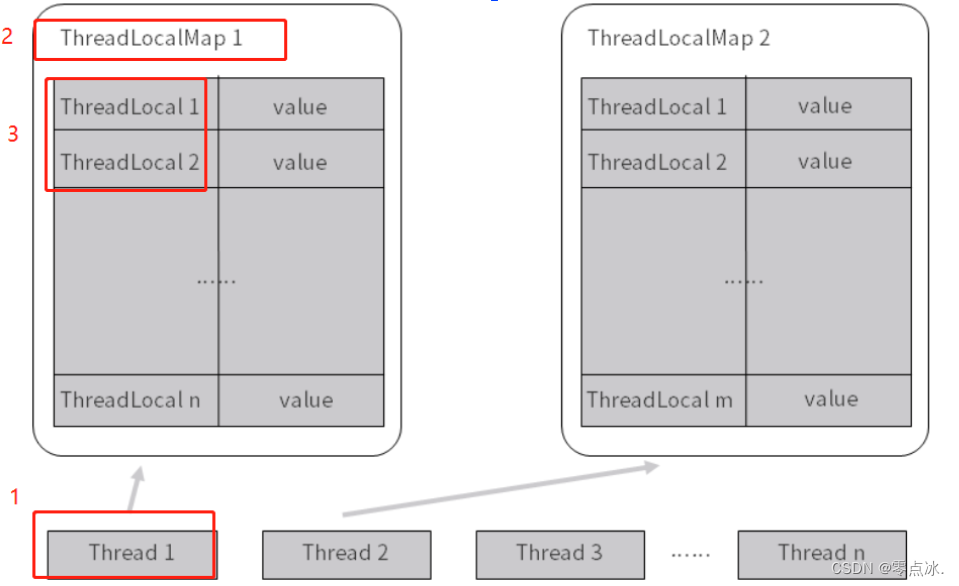
目录 1、线程基础 1.1、线程实现方法 1.2、如何正确停止线程 1.3、Java线程的六种状态 1.4、wait/notify/notifyAll注意事项 1.4.1、为什么 wait 、notify、notifyAll必须在 synchronized 保护的同步代码中使用? 1.4.2、为什么 wait/notify/notifyAll 被定义…...
QT之OpenGL混合
QT之OpenGL混合1. 概述2. 实现2.1 丢弃片段2.1.1 Demo2.2 混合2.2.1 相关函数2.2.2 排序问题2.2.3 Demo1. 概述 OpenGL中,混合(Blending)通常是实现物体透明度(Transparency)的一种技术。 2. 实现 2.1 丢弃片段 在某些情况下,有些片段是只需要设置显…...

【1255. 得分最高的单词集合】
来源:力扣(LeetCode) 描述: 你将会得到一份单词表 words,一个字母表 letters (可能会有重复字母),以及每个字母对应的得分情况表 score。 请你帮忙计算玩家在单词拼写游戏中所能获…...

nginx模块介绍
新编译前,在对应的nginx原编译文件夹 如:nginx-1.23.0 下,要 make clean 清空以前编译的objs文件夹,实际上就是执行了rm objs文件夹。 很多要用到git,先yum install git -y echo-nginx-module 让nginx直接使用echo的…...
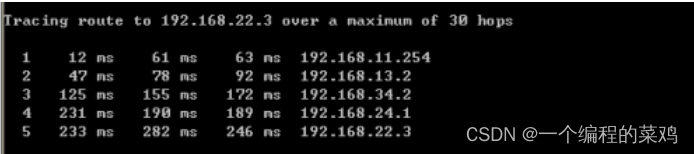
排错工具ping和trace(电子科技大学TCP/IP实验四)
一.实验目的 1、了解网络连通性测试的方法和工作原理 2、了解网络路径跟踪的方法和工作原理 3、掌握 MTU 的概念和 IP 分片操作 4、掌握 IP 分组生存时间(TTL)的含义和作用 5、掌握路由表的作用和路由查找算法 二.预备知识 …...

node.js中ws模块创建服务端和客户端
一、WebSocket出现的原因 1、Http协议发布REST API 的不足: 每次请求响应完成之后,服务器与客户端之间的连接就断开了,如果客户端想要继续获取服务器的消息,必须再次向服务器发起请 求。这显然无法适应对实时通信有高要求的场景…...

kubernates-1.26.1 kubeadm containerd 单机部署
k8s1.26 kubeadm containerd 安装 kubeadm init 时提示 containerd 错误 failed to pull image “k8s.gcr.io/pause:3.6” 报错日志显示containerd pull时找不到对应的pause版本,而不是registry.k8s.io/pause:3.9 [rootk8s-master containerd]# kubeadm init --k…...
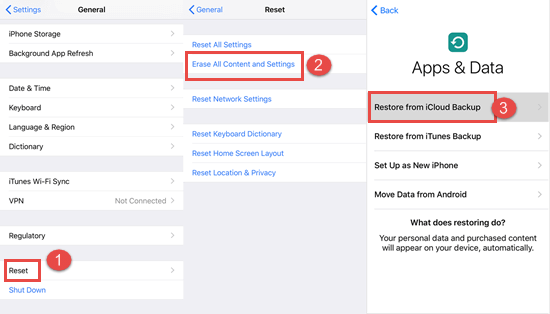
如何在 iPhone 上恢复已删除的通话记录/通话记录
您的通话记录/通话记录可能很重要,尤其是当您想要拨打之前联系过但未保存的号码时。如果您碰巧删除了通话记录(有意或无意),本指南将帮助您了解如何检索它们并找回您需要使用的所有记录。我们将根据您的情况和您拥有的工具讨论不同…...
Canonical为所有支持的Ubuntu LTS系统发布了新的Linux内核更新
导读Canonical近日为所有支持的Ubuntu LTS系统发布了新的Linux内核更新,以解决总共19个安全漏洞。新的Ubuntu内核更新仅适用于长期支持的Ubuntu系统,包括Ubuntu 22.04 LTS(Jammy Jellyfish)、Ubuntu 20.04 LTS(Focal F…...
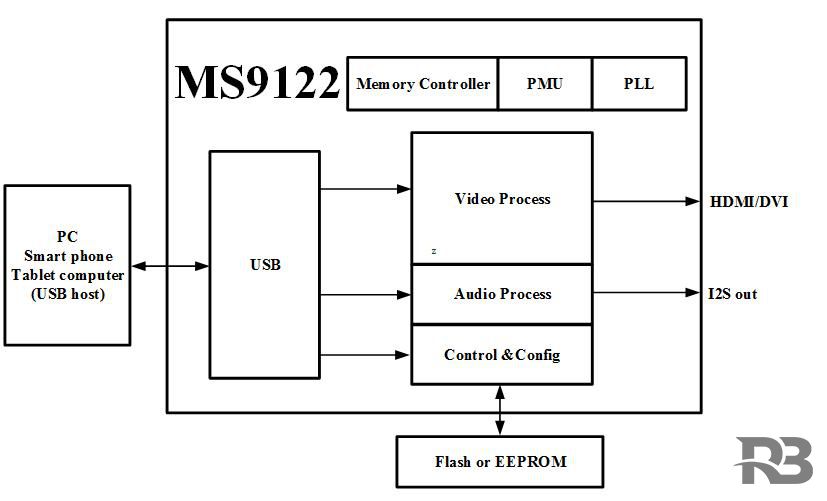
MS9122是一款USB单芯片投屏器,内部集成了USB2 0 控制器和数据收发模块、HDMI 数据接口和音视频处理模块。MS9122可以通过USB接口显示
MS9122是一款USB单芯片投屏器,内部集成了USB2.0 控制器和数据收发模块、HDMI 数据接口和音视频处理模块。MS9122可以通过USB接口显示或者扩展PC、智能手机、平板电脑的显示信息到更大尺寸的显示设备,支持HDMI视频接口。 主要功能特征 HDMI v1.4兼容 最大…...

C++学习笔记-数据抽象
简单的说,数据抽象是用来描述数据结构的。数据抽象就是 ADT。一个 ADT 主要表现为它支持的一些操作,比方说 stack.push、stack.pop,这些操作应该具有明确的时间和空间复杂度。另外,一个 ADT 可以隐藏其实现细节,比方说…...

【Android】Android开发笔记(一)
【Android】Android开发笔记(一) 在Android Studio中import module和delete moduleimport moduledelete moduleAndroid Studio中App(Module)无法正常运行在实机上测试App一些基本概念App的工程结构结语在Android Studio中import m…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
