高数考试必备知识点
三角函数与反三角函数的知识点
-
正弦函数 y=sin x, 反正弦函数 y=arcsin x
• y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
• y = arcsin x, x∈[–1,1], y∈[–π/2,π/2] -
sin x = 0 ←→ arcsin x = 0
-
sin x = 1/2 ←→ arcsin x = π/6
-
sin x = √2/2 ←→ arcsin x = π/4
-
sin x = 1 ←→ arcsin x = π/2
-
余弦函数 y=cos x, 反余弦函数 y=arccos x
• y = cos x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = kπ 为对称轴
• y = arccos x, x∈[–1,1], y∈[0,π] -
cos x = 0 ←→ arccos x = π/2
-
cos x = 1/2 ←→ arccos x = π/3
-
cos x = √2/2 ←→ arccos x = π/4
-
cos x = 1 ←→ arccos x = 0
-
反正弦函数 y=arcsin x, 反余弦函数 y=arccos x
y = arcsin x 与 y = arccos x 自变量的取值范围都是 x∈[–1,1]
y = arcsin x 与 y = arccos x 的图像关于直线 y = π/4 对称,相交与点 (√2/2 ,π/4) -
正切函数 y=tan x, 余切函数 y=cot x
• y = tan x, x∈( (–π/2) + kπ, (π/2) + kπ ), y∈R,周期为π,当 x → ± (π/2) + kπ 时,函数的极限是无穷大 ∞
• y = cot x = 1 / tan x, x∈( 0,kπ ), y∈R,周期为π,当 x → kπ 时,函数的极限是无穷大 ∞
• y = tan x 与 y = cot x 的图像关于 x = (π/4) + kπ/2 对称
• 在单个周期内(第一个),y = tan x 与 y = cot x 的图像相交与点 (π/4 ,1)。当 x = (π/4) + kπ/2 时,y = tan x 与 y = cot x 函数的值都相等,等于 ±1 -
反正切函数 y=arctan x, 反余切函数 y=arccot x
• y = arctan x 与 y = arccot x 自变量的取值范围都是 x∈R
• y = arctan x 与 y = arccot x 的图像关于直线 y = π/4 对称,相交与点 (1 ,π/4)
- tan x = 0 ←→ arctan x = 0
- tan x = 1 ←→ arctan x = π/4
- tan x = √3 ←→ arctan x = π/3
- 余割函数 y=csc x
• y = csc x = 1 / sin x,x∈(0,kπ ), y∈(–∞,–1]∪[1,∞),周期为π,当 x → kπ 时,函数的极限是无穷大 ∞ - 正割函数 y=sec x
• y = sec x = 1 / cos x,x∈( (–π/2) + kπ, (π/2) + kπ ), y∈(–∞,–1]∪[1,∞),周期为π,当 x → (π/2) + kπ 时,函数的极限是无穷大 ∞。
函数
1.1函数及其性质
映射:非空集合X、Y,若存在一个法则f,使X中每个元素x在Y中有唯一确定的数y与之对应,则称f为从X到Y的映射。
(单射、满射、双射、逆映射、复合映射)
函数:D为实数集,则映射 为定义在D上的函数。
(定义域对应的函数值只有一个的函数为单值函数,否则为多值函数)
疑问:多值函数(如: )为一对多的映射情况,可这种映射不符合映射的定义,故多值函数还算函数吗?
函数特性:单调性、有界性、奇偶性、周期性。
1.2 数列的极限
数列极限:设有数列 及常数a,若 ,当 时有 成立,则称a是数列 的极限或称 收敛于a。
记为 ,其几何解释为所有下标大于N的项都落在a的邻域内。
(数列极限的定义只能验证,不能求解)
数列极限性质:唯一性、有界性、保号性。
1.3 函数的极限
函数极限:
(1) 自变量趋于无穷大时
设f(x)定义在 上,A是一个确定的数,
若 ,使当|x| > X时,恒有|f(x) - A|<,则称A是f(x)当时的极限。
记为
(2) 自变量趋于有限值时
设f(x)在 的某去心邻域内有定义,A是一个确定的数,
若 ,使当 时,恒有|f(x) - A|< ,则称A是f(x)当时的极限。
记为 (左极限、右极限)
(函数极限证明通过定义,与数列极限证明同理)
函数极限性质:唯一性、局部有界性、局部保号性。
1.4 极限的运算法则
函数极限四则运算法则:若 , , 则
(1)
(2)
(3)
数列极限四则运算法则:与函数法则同理。
复合函数极限运算法则:
常用结论: (1) (2)
(3) (4)
(5) P(x),Q(x)为多项式函数,求 若 ,则 若 , 则把P(x),Q(x)因式分解约去公因式后再处理 若 , , 则
(6) 一般地,当 ,m和n为非负整数时有 (分子分母同除 )
当n=m, 当n>m, 0,
当n<m, 当
1.5 极限存在准则 两个重要极限
(1) 夹逼准则:在给定的变化过程中,如果g(x),f(x),h(x)满足
① 则 ②
(2) 单独有界准则:单调有界数列必有极限(单调递增(减)数列只需上(下)有界)
(3) Cauchy收敛准则:数列{undefined }收敛的充分必要条件时
,使得当 m > N , n > N时,有 。
满足上述条件的数列也称Cauchy数列或基本数列。
(4) 第一重要极限:
(5) 第二重要极限:
1.6 无穷小与无穷大
无穷小:若 , 则称f(x)当 时为无穷小。(如 )
若 ,当 时 |f(x)| < ,则称f(x)当时为无穷小。
(1) 数 “0” 是无穷小量。
(2) 无穷小并不是一个很小的数,其是一类特殊函数,是在某一变化过程中极限为0的函数,并且在一个过程中为无穷小的量在另一过程中可能不是无穷小量。
(3) , 其中 。
无穷大:若 ,则称f(x)当 时为无穷大。(如 )
若 ,当 时 |f(x)| > M,则称f(x)当时为无穷大。
(1) 无穷大是变量,不能与很大的数混淆。
(2) 切勿将 认为极限存在。
二者关系:在自变量的同一变化过程中,如果f(x)为无穷大,则 为无穷小。反之,如果f(x)为无穷小,且 ,则为无穷大。
定理:(1) 有限个无穷小的代数和(乘积)仍为无穷小(无限个无穷小的代数和未必是无穷小;n 个 为1)。
(2) 有界函数与无穷小的乘积是无穷小。
(3) 有限个无穷大的乘积是无穷大(两个无穷大的和与差不一定是无穷大;) 。
(4) 无穷大与有界函数之和是无穷大(无穷大与有界函数乘积不一定无穷大;)。
无穷小阶:设 , 且 。
(1) 如果 , 就说 是比 高阶的无穷小;
(2) 如果 , 就说 是比 低阶的无穷小;
(3) 如果 , 就说 与 是同阶的无穷小;
(4) 如果 , 就说 与 是等价的无穷小;
(5) 如果 , 就说 是 比的k阶的无穷小;
等价无穷小替换定理:设 , 且 存在,则 。
(1) 等价无穷小代换只适用于乘积中(代数和或复合函数不可应用);
(2) 常用等价无穷小(当 时)
sin x~x , tan x~x arcsin x~x arctan x~ x ln(1+x) x -1~x 1-cos x~
1.7 函数连续
函数连续定义:设函数y=f(x)在点 的某一邻域内有定义, ,则函数f(x)在 处连续。
① 在x= 处有定义。
② lim f(x)存在,lim f(x)=f( )
函数间断定义:①在x= 没有定义; ②虽在x= 有定义但lim f(x)不存在; ③虽在x= 有定义且在lim f(x)存在,但lim f(x)≠f( )。
函数间断点的分类:第一类间断点,第二类间断点。
第一类:无穷间断点、可去间断点、振荡间断点
1.8 连续函数的运算与初等函数的连续性
1、如果函数f(x)与g(x)在点 连续,那么它们的和差积商都在点 连续。
2、如果f(x)在某区间内单调递增且连续,那么它的反函数也在此区间内单调递增且连续。
3、复合函数f[g(x)],g(x)连续,那么f[g(x)]也连续。
一切初等函数在定义域内都是连续。
相关文章:

高数考试必备知识点
三角函数与反三角函数的知识点 正弦函数 ysin x, 反正弦函数 yarcsin x • y sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x (π/2) kπ 为对称轴 • y arcsin x, x∈[–1,1]…...
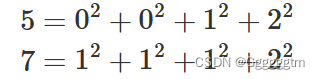
[蓝桥杯] 二分与前缀和习题练习
文章目录 一、二分查找习题练习 1、1 数的范围 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 机器人跳跃问题 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 四平方和 1、3、1 题目描述 1、3、2 题解关键思路与解答 二、前缀和习题练习 2、1 前缀和 2、1、1 题目描述…...
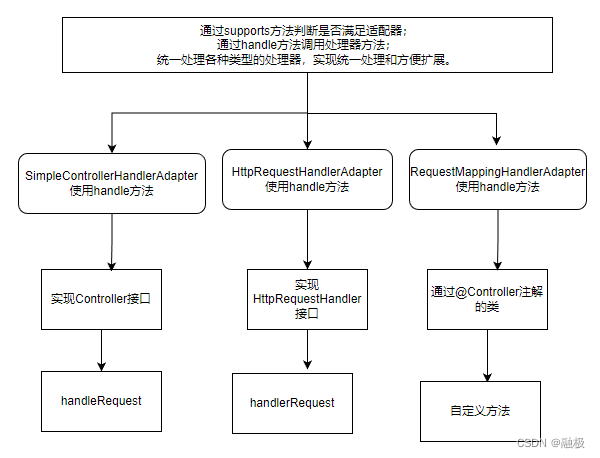
SpringMvc中HandlerAdapter组件的作用
概述 我们在使用springMVC时,都知道其中不仅包含handlerMapping组件还包含handlerAdapter组件,为什么呢? springMVC请求流程图 HandlerAdapter组件使用了适配器模式 适配器模式的本质是接口转换和代码复用,这里使用适配器模式的…...
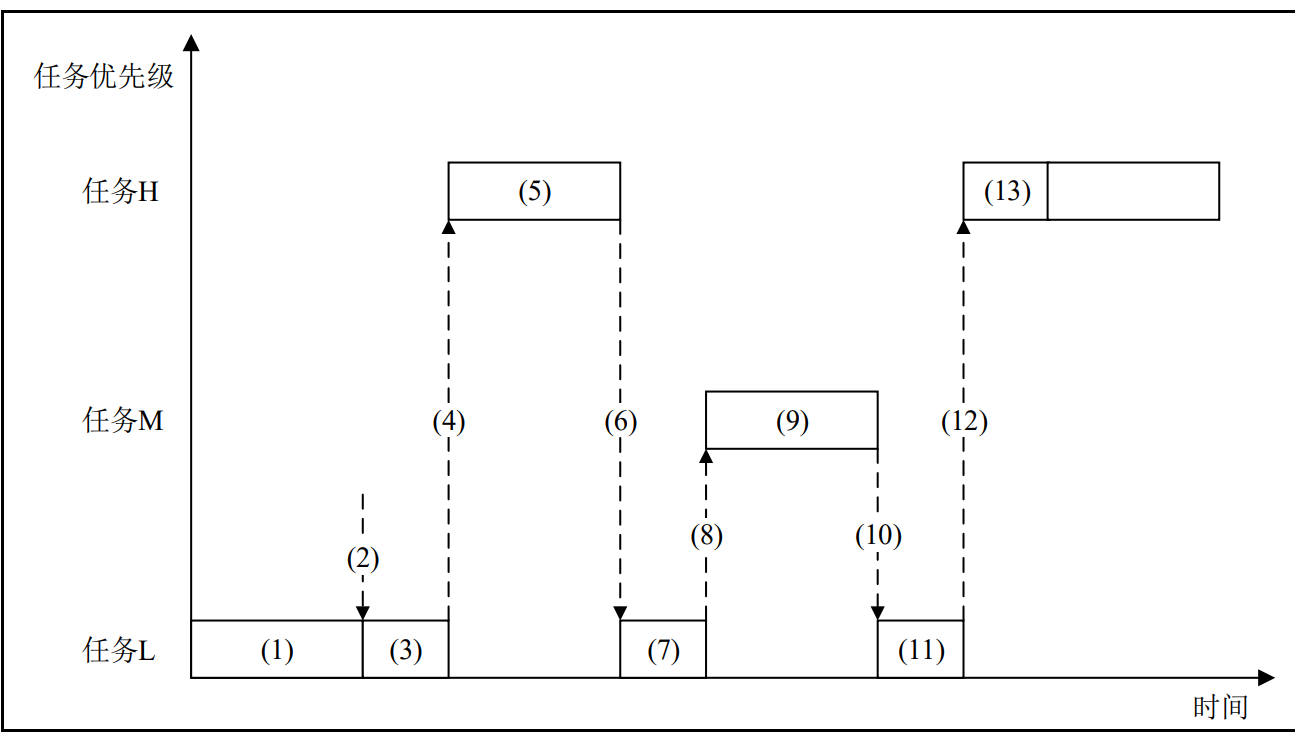
FreeRTOS优先级翻转
优先级翻转优先级翻转:高优先级的任务反而慢执行,低优先级的任务反而优先执行优先级翻转在抢占式内核中是非常常见的,但是在实时操作系统中是不允许出现优先级翻转的,因为优先级翻转会破坏任务的预期顺序,可能会导致未…...

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springbootvue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自…...

golang项目----家庭收支记账软件
家庭收支记账软件实现基本功能(先使用面向过程,后面改成面向对象)项目代码实现改进面向过程源码面向对象源码utils包中main包中实现基本功能(先使用面向过程,后面改成面向对象) 编写文件TestMyAccount.go完成基本功能 功能一:先完成可以显示…...

中国LNG市场投资机会研究
中国LNG市场投资机会研究中国LNG市场是一个具有巨大潜力和发展机遇的市场,尤其是在政府大力推动清洁能源发展的背景下,LNG市场投资机会正在不断扩大。首先,政府大力支持LNG市场的发展。政府实施的“十三五”规划将LNG作为清洁能源的重要来源&…...
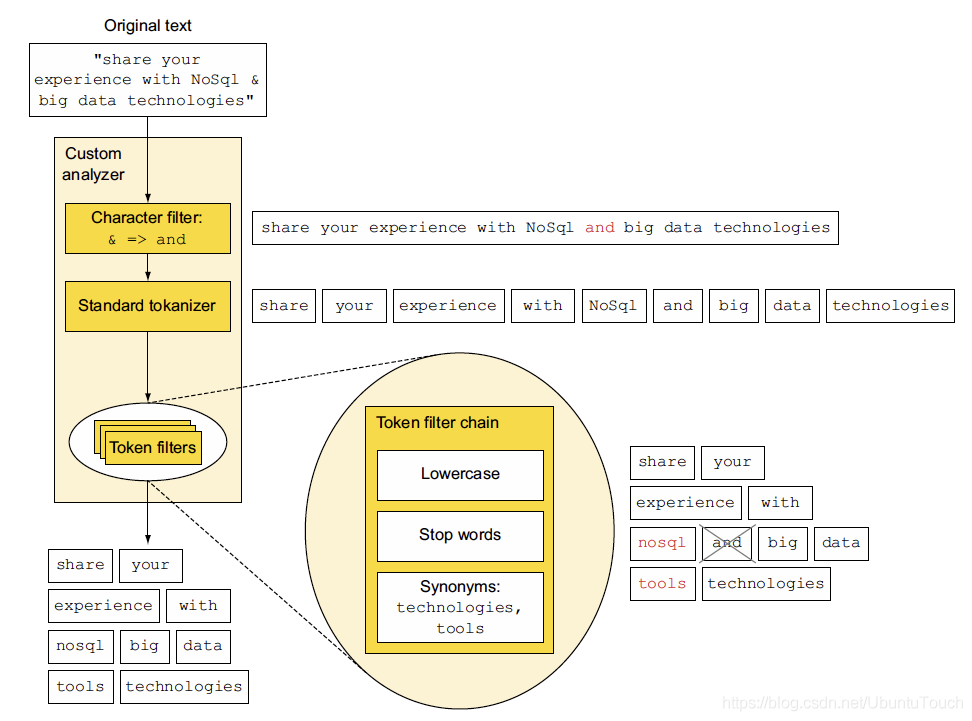
Elasticsearch:索引数据是如何完成的
在我在之前的文章 “Elasticsearch:彻底理解 Elasticsearch 数据操作” 文章中,我详细地描述了如何索引数据到 Elasticsearch 中。在今天的文章中,我想更进一步来描述这个流程。 Elasticsearch 是一个非常强大和灵活的分布式数据系统&#x…...

处理器管理
处理器状态处理器管理是操作系统中重要组成部分,负责管理、调度和分配计算机系统的重要资源——处理器,并控制程序执行由于处理器管理是操作系统最核心的部分,无论是应用程序还是系统程序,最终都要在处理器上执行以实现其功能&…...
第五)
跟着我从零开始入门FPGA(一周入门系列)第五
5、同步和异步设计 前面已有铺垫,同步就是与时钟同步。 同步就是走正步,一二一,该迈哪个脚就迈那个脚,跑的快的要等着跑的慢的。 异步就是搞赛跑,各显神通,尽最大力量去跑,谁跑得快,…...

【第42天】Arrays.sort 与 Collections.sort 应用 | 整形数组与集合的排序
本文已收录于专栏🌸《Java入门一百练》🌸学习指引序、专栏前言一.sort函数二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析三、推荐专栏序、专栏前言 本专栏开启,目的…...

LeetCode第334场周赛
2023.2.26LeetCode第334场周赛 A. 左右元素和的差值 思路 前缀和后缀和 代码 class Solution { public:vector<int> leftRigthDifference(vector<int>& nums) {int n nums.size();vector<int> l(n), r(n), ans(n);for (int i 1; i < n; i )l[…...
:PatchMatchNet配置及代码主要运行流程)
基于深度学习的三维重建网络PatchMatchNet(三):PatchMatchNet配置及代码主要运行流程
目录 1.PatchMatchNet环境配置 2. PatchMatchNet的大致执行流程(eval.py) 2.1 深度图的保存...

【一天一门编程语言】设计一门编程语言,给出基础语法代码示例,SDK设计。
文章目录设计一门编程语言,给出基础语法代码示例,SDK设计。一、编程语言设计1.1 语言名称1.2 数据类型1.3 基本运算符1.4 控制语句二、SDK设计2.1 基础库2.2 第三方库三、例子用 Mango 这门语言实现斐波那契数列。基础语法代码示例SDK 设计使用 Mango 语…...

ubuntu 下 python 安装 venv
ubuntu 下 python 安装 venv1.首先,确保您的系统已安装 Python3 和 pip3,如果没有安装,可以使用以下命令安装:2. 接着,安装 virtualenv 包,使用以下命令:3.创建 Python 虚拟环境,使用…...

HTML#1快速入门
一. 简介HTML是一门语言, 所有的网页都是用HTML编写的HTML(Hyper Text Markup Language): 超文本(超越了文本限制,除了文字信息还可以定义图片,音频,视频等)标记语言(有标签构成的语言)W3C标准: 网页主要由三部分组成(1) 结构: HTML(2) 表现: CSS(3) 行为: JavaScript二. 快速入…...
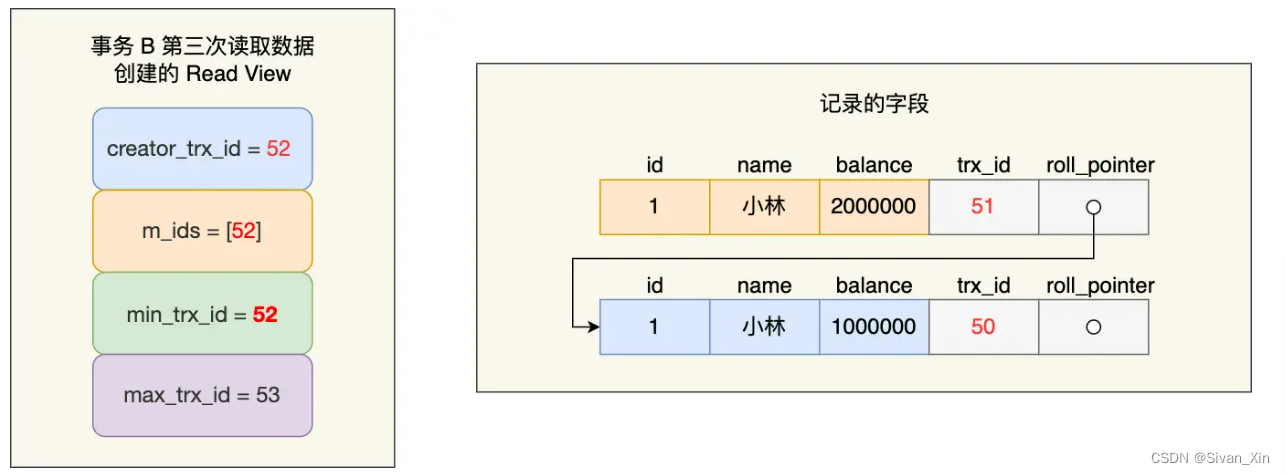
【MySQL】事务隔离级别是怎么实现的?
事务隔离级别是怎么实现的? 四种隔离级别具体的实现方式 对于「读未提交」:直接读取最新的数据就好。对于「串行化」:通过加读写锁的方式来避免并行访问。对于「读提交」和「可重复读」:通过 Read View 来实现,主要区…...
JSP网上书店系统用myeclipse定制开发mysql数据库B/S模式java编程计算机网页
一、源码特点 JSP 网上书店系统 是一套完善的系统源码,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。研究的基本内容是基于网上书店系 统,使用JSP作为页面开发工具。Web服务的运…...

配置 Haproxy 负载均衡群集
配置 haproxy 负载均衡群集 🏆荣誉认证:51CTO博客专家博主、TOP红人、明日之星;阿里云开发者社区专家博主、技术博主、星级博主。 💻微信公众号:微笑的段嘉许 📌本文由微笑的段嘉许原创! &#…...
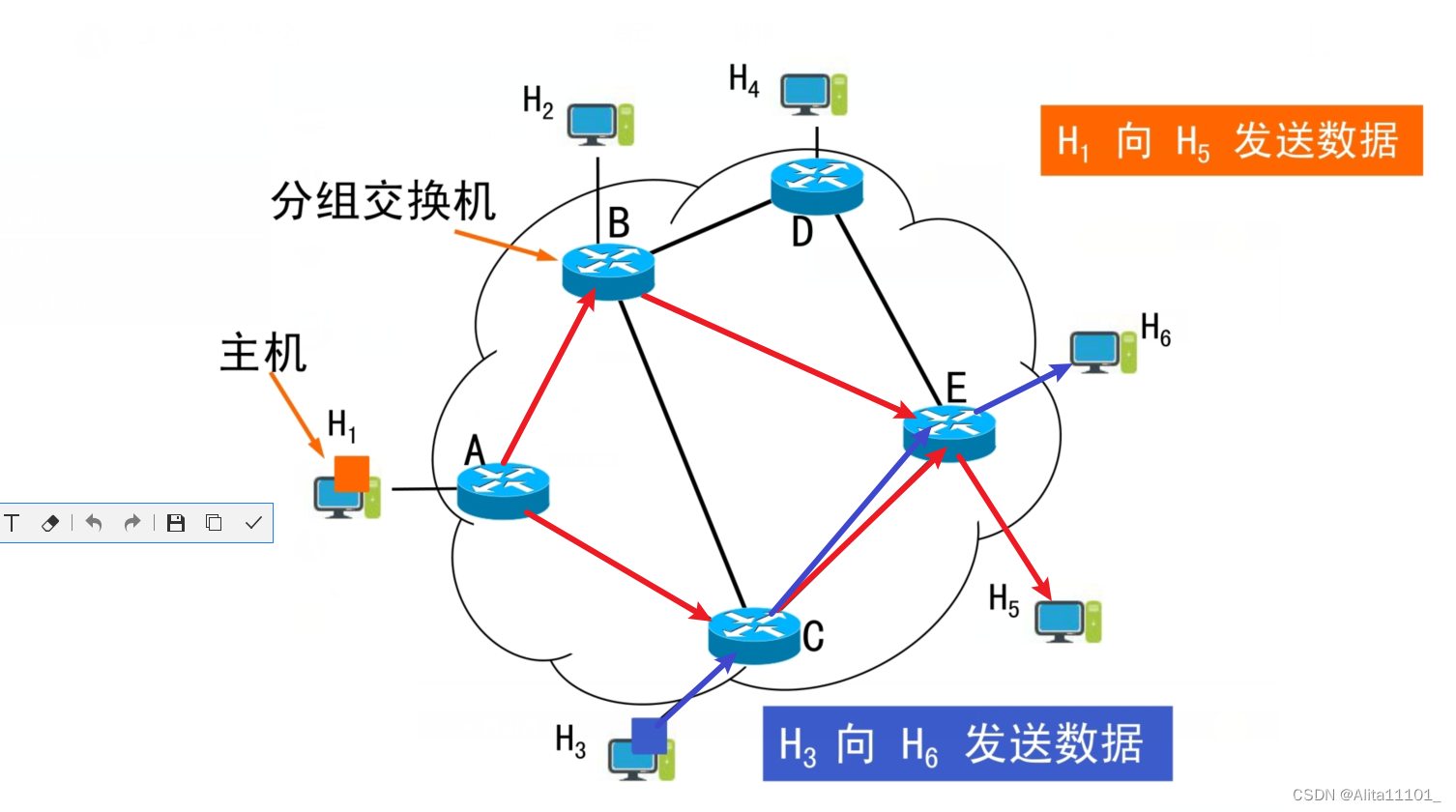
计算机网络笔记 | 第一章:计算机网络概述(1.1-1.4小节知识点整理)
从专栏将讲述有关于计算机网络相关知识点,如果有想学习Java的小伙伴可以点击下方连接查看专栏,还有JavaEE部分 本专栏地址(持续更新中):🔥计算机网络 MyBatis:✍️MyBatis Java入门篇࿱…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
