buu [GWCTF 2019]BabyRSA 1
题目描述:
import hashlib
import sympy
from Crypto.Util.number import *flag = 'GWHT{******}'
secret = '******'assert(len(flag) == 38)half = len(flag) / 2flag1 = flag[:half]
flag2 = flag[half:]secret_num = getPrime(1024) * bytes_to_long(secret)p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)N = p * qe = 0x10001F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)m1 = pow(c1, e, N)
m2 = pow(c2, e, N)output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
题目分析:
对代码进行分析可得大致加密过程为:
- 首先给了字符串明文flag和secret,然后对flag对半切得到flag1和flag2
- 随机生成一个1024位(2进制)的素数,并将secret(字符串)类型转化为整数类型,然后将这两个结果相乘得到secret_num
拓展:
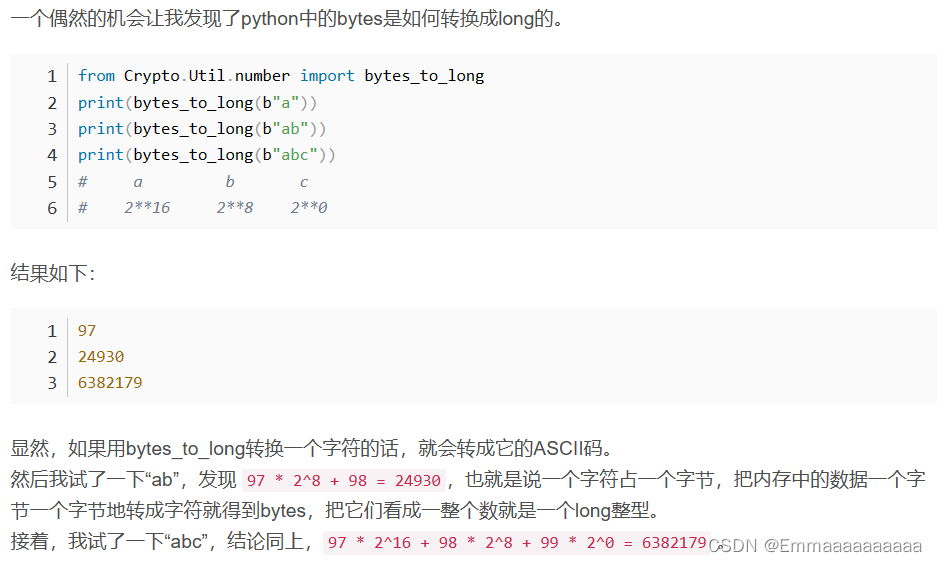
bytes_to_long(x) —> 字节转整数 (会将字节x转化为它的ascii码)
long_to_bytes(x) —> 整数转字节
- 取secret_num的下一个素数作为p,取p的下一个素数作为q,得到N=p*q
必备知识:
sympy.prevprime(x)是求大于x最近的质数
sympy.nextprime(x)是求小于x最近的质数
- 将flag1和flag2通过bytes_to_long转化为整数得到F1和F2
- 将F1,F2设计成方程组得到c1,c2,进一步加密得到m1,m2
- 最后给出运行结果得到 N,m1,m2
decrypt(解密)
- 题中给出了N,通过以上分析可以得知p,q是两个相邻的素数,所以对N进行开方运算(iroot(N,2))后可以得到一个值x,并且pq
- 通过sympy.prevprime(x),sympy.nextprime(x) 函数可以得到p,q,从而可以求得d
- 然后进行RSA解密得出c1和c2
c1 = pow(m1,d,N)
c2 = pow(m2,d,N)
- 至此,我们得到一个方程组:
c1=F1+F2
c2=F13+F23
- 利用sympy库进行方程组求解:
from sympy import *
F1 = Symbol('F1')
F2 = Symbol('F2')
F1,F2 = solve([F1+F2-c1,(F1)**3+(F2)**3-c2])
得到:
{F1: 1141553212031156130619789508463772513350070909, F2: 1590956290598033029862556611630426044507841845},
{F1: 1590956290598033029862556611630426044507841845, F2: 1141553212031156130619789508463772513350070909}
- 得到两组解,但仔细看只是调换的位置而已,两组都试一下,便可得到最终flag
- 完整代码:
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
e = 65537
import gmpy2
import libnum
import sympy.crypto.crypto
x = gmpy2.iroot(N,2)[0]
p = sympy.nextprime(x)
q = N//p
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
# m1 = pow(c1, e, N)
# m2 = pow(c2, e, N)
c1 = pow(m1,d,N)
c2 = pow(m2,d,N)
from sympy import *
F1 = Symbol('F1')
F2 = Symbol('F2')
print(solve([F1+F2-c1,(F1)**3+(F2)**3-c2]),F1,F2)
F1,F2 = solve([F1+F2-c1,(F1)**3+(F2)**3-c2])
F2 = 1141553212031156130619789508463772513350070909
F1 = 1590956290598033029862556611630426044507841845
print(libnum.n2s(int(F1))+libnum.n2s(int(F2)))
- 最后得到flag{f709e0e2cfe7e530ca8972959a1033b2}
收获与体会:
- 了解了bytes_to_long(x) 与 long_to_bytes(x) 相关知识
- 代码中有一步有点一知半解
m1 = pow(c1, e, N)
m2 = pow(c2, e, N)
---->(这里有点迷)
c1 = pow(m1,d,N)
c2 = pow(m2,d,N)
相关文章:
buu [GWCTF 2019]BabyRSA 1
题目描述: import hashlib import sympy from Crypto.Util.number import *flag GWHT{******} secret ******assert(len(flag) 38)half len(flag) / 2flag1 flag[:half] flag2 flag[half:]secret_num getPrime(1024) * bytes_to_long(secret)p sympy.nextp…...

codeforces 1669F
题意: alice和bob从数组两边的吃糖果, 数组的值就是糖果重量 要求alice和bob吃的糖果重量必须一样, 输出能吃几个糖果 这题最先想到的是前后缀相加 模拟一个前缀和 和 后缀和 在n/2的位置向前找前缀和 在n/2的位置向后找后缀和 找到第一个前缀和后缀和的下标输出就好 …...

高数考试必备知识点
三角函数与反三角函数的知识点 正弦函数 ysin x, 反正弦函数 yarcsin x • y sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x (π/2) kπ 为对称轴 • y arcsin x, x∈[–1,1]…...
[蓝桥杯] 二分与前缀和习题练习
文章目录 一、二分查找习题练习 1、1 数的范围 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 机器人跳跃问题 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 四平方和 1、3、1 题目描述 1、3、2 题解关键思路与解答 二、前缀和习题练习 2、1 前缀和 2、1、1 题目描述…...
SpringMvc中HandlerAdapter组件的作用
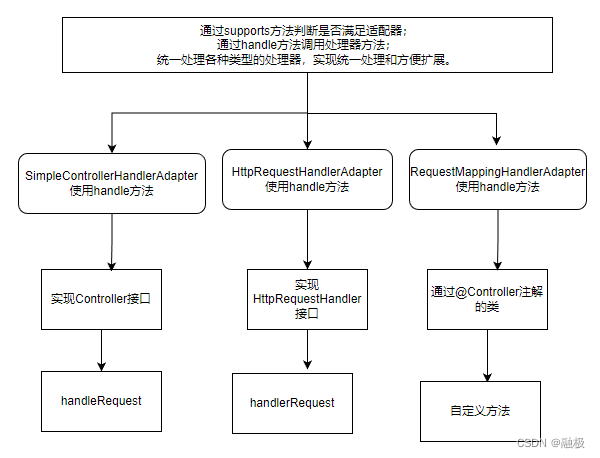
概述 我们在使用springMVC时,都知道其中不仅包含handlerMapping组件还包含handlerAdapter组件,为什么呢? springMVC请求流程图 HandlerAdapter组件使用了适配器模式 适配器模式的本质是接口转换和代码复用,这里使用适配器模式的…...
FreeRTOS优先级翻转
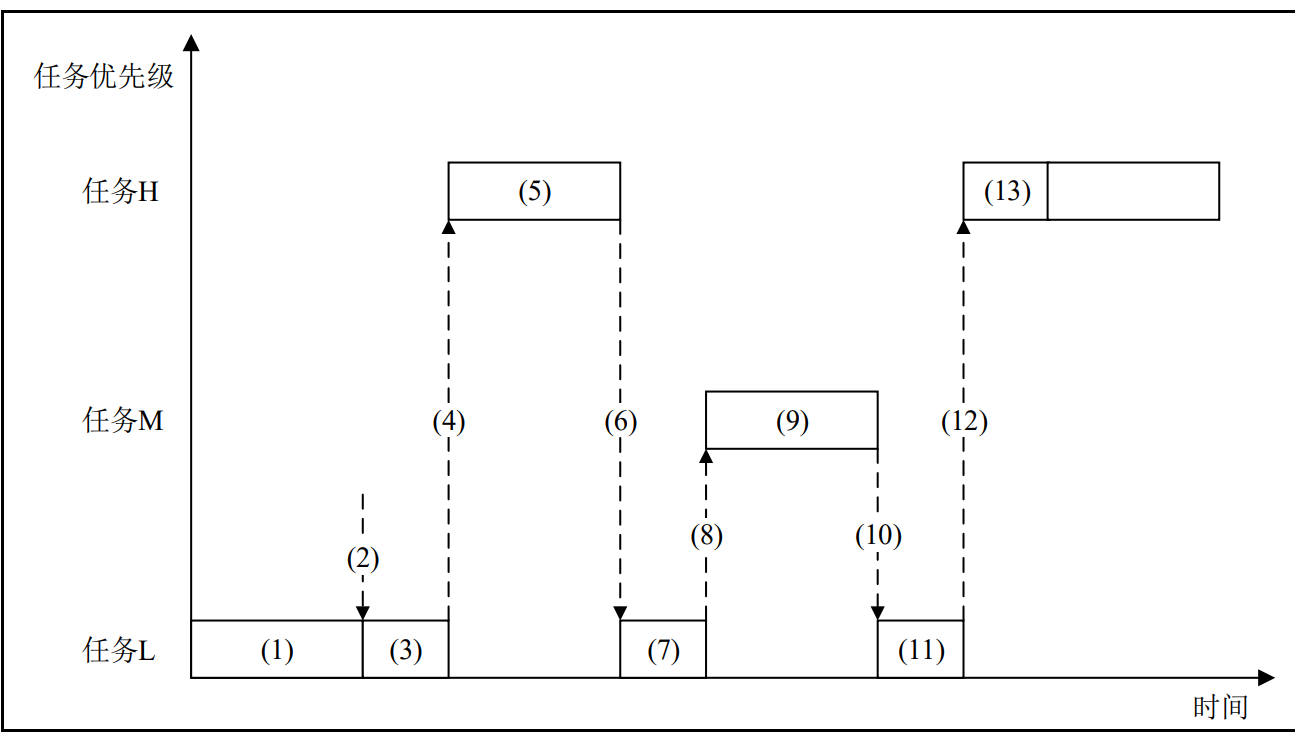
优先级翻转优先级翻转:高优先级的任务反而慢执行,低优先级的任务反而优先执行优先级翻转在抢占式内核中是非常常见的,但是在实时操作系统中是不允许出现优先级翻转的,因为优先级翻转会破坏任务的预期顺序,可能会导致未…...

服务器部署—部署springboot之Linux服务器安装jdk和tomcat【建议收藏】
我是用的xshell连接的云服务器,今天想在服务器上面部署一个前后端分离【springbootvue】项目,打开我的云服务器才发现,过期了,然后又买了一个,里面环境啥都没有,正好出一期教程,方便大家也方便自…...

golang项目----家庭收支记账软件
家庭收支记账软件实现基本功能(先使用面向过程,后面改成面向对象)项目代码实现改进面向过程源码面向对象源码utils包中main包中实现基本功能(先使用面向过程,后面改成面向对象) 编写文件TestMyAccount.go完成基本功能 功能一:先完成可以显示…...

中国LNG市场投资机会研究
中国LNG市场投资机会研究中国LNG市场是一个具有巨大潜力和发展机遇的市场,尤其是在政府大力推动清洁能源发展的背景下,LNG市场投资机会正在不断扩大。首先,政府大力支持LNG市场的发展。政府实施的“十三五”规划将LNG作为清洁能源的重要来源&…...
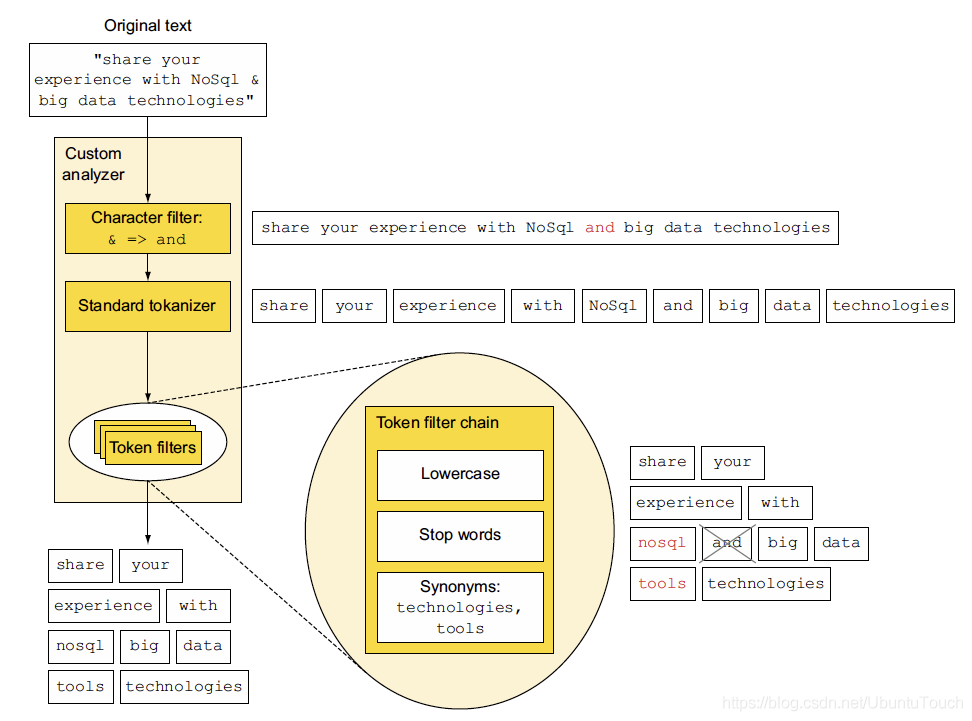
Elasticsearch:索引数据是如何完成的
在我在之前的文章 “Elasticsearch:彻底理解 Elasticsearch 数据操作” 文章中,我详细地描述了如何索引数据到 Elasticsearch 中。在今天的文章中,我想更进一步来描述这个流程。 Elasticsearch 是一个非常强大和灵活的分布式数据系统&#x…...

处理器管理
处理器状态处理器管理是操作系统中重要组成部分,负责管理、调度和分配计算机系统的重要资源——处理器,并控制程序执行由于处理器管理是操作系统最核心的部分,无论是应用程序还是系统程序,最终都要在处理器上执行以实现其功能&…...
第五)
跟着我从零开始入门FPGA(一周入门系列)第五
5、同步和异步设计 前面已有铺垫,同步就是与时钟同步。 同步就是走正步,一二一,该迈哪个脚就迈那个脚,跑的快的要等着跑的慢的。 异步就是搞赛跑,各显神通,尽最大力量去跑,谁跑得快,…...

【第42天】Arrays.sort 与 Collections.sort 应用 | 整形数组与集合的排序
本文已收录于专栏🌸《Java入门一百练》🌸学习指引序、专栏前言一.sort函数二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析三、推荐专栏序、专栏前言 本专栏开启,目的…...

LeetCode第334场周赛
2023.2.26LeetCode第334场周赛 A. 左右元素和的差值 思路 前缀和后缀和 代码 class Solution { public:vector<int> leftRigthDifference(vector<int>& nums) {int n nums.size();vector<int> l(n), r(n), ans(n);for (int i 1; i < n; i )l[…...
:PatchMatchNet配置及代码主要运行流程)
基于深度学习的三维重建网络PatchMatchNet(三):PatchMatchNet配置及代码主要运行流程
目录 1.PatchMatchNet环境配置 2. PatchMatchNet的大致执行流程(eval.py) 2.1 深度图的保存...

【一天一门编程语言】设计一门编程语言,给出基础语法代码示例,SDK设计。
文章目录设计一门编程语言,给出基础语法代码示例,SDK设计。一、编程语言设计1.1 语言名称1.2 数据类型1.3 基本运算符1.4 控制语句二、SDK设计2.1 基础库2.2 第三方库三、例子用 Mango 这门语言实现斐波那契数列。基础语法代码示例SDK 设计使用 Mango 语…...

ubuntu 下 python 安装 venv
ubuntu 下 python 安装 venv1.首先,确保您的系统已安装 Python3 和 pip3,如果没有安装,可以使用以下命令安装:2. 接着,安装 virtualenv 包,使用以下命令:3.创建 Python 虚拟环境,使用…...

HTML#1快速入门
一. 简介HTML是一门语言, 所有的网页都是用HTML编写的HTML(Hyper Text Markup Language): 超文本(超越了文本限制,除了文字信息还可以定义图片,音频,视频等)标记语言(有标签构成的语言)W3C标准: 网页主要由三部分组成(1) 结构: HTML(2) 表现: CSS(3) 行为: JavaScript二. 快速入…...
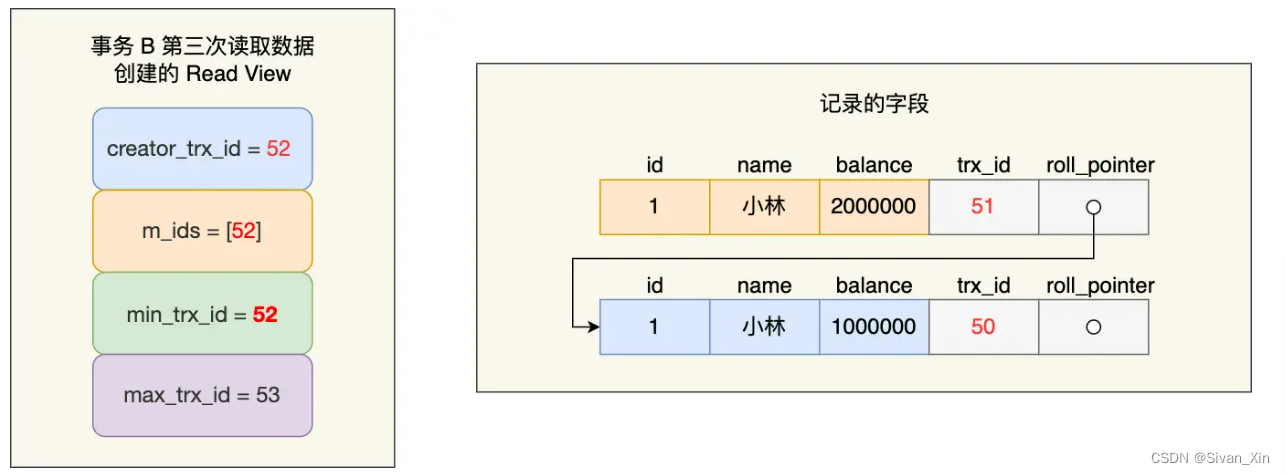
【MySQL】事务隔离级别是怎么实现的?
事务隔离级别是怎么实现的? 四种隔离级别具体的实现方式 对于「读未提交」:直接读取最新的数据就好。对于「串行化」:通过加读写锁的方式来避免并行访问。对于「读提交」和「可重复读」:通过 Read View 来实现,主要区…...
JSP网上书店系统用myeclipse定制开发mysql数据库B/S模式java编程计算机网页
一、源码特点 JSP 网上书店系统 是一套完善的系统源码,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。研究的基本内容是基于网上书店系 统,使用JSP作为页面开发工具。Web服务的运…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
