509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
class Solution {
public:int fib(int n) {//定义dp数组的意思//状态//初始化//遍历顺序//dp数组值是否符合if(n < 2) return n;// 表示第一个斐波那契数为dp[i];vector<int>dp(n+1); // 因为下面直接访问dp[0]和dp[1],所以得先加内存。dp[0] = 0;dp[1] = 1;for(int i = 2;i <= n;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
};相关文章:

509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 n > 1给定 n &a…...

四、[mysql]索引优化-1
目录 前言一、场景举例1.联合索引第一个字段用范围查询不走索引(分情况)2.强制走指定索引3.覆盖索引优化4.in和or在表数据量比较大的情况会走索引,在表记录不多的情况下会选择全表扫描5.like 后% 一般情况都会走索引(索引下推) 二、Mysql如何选择合适的索…...
:神经网络-最大池化使用)
PyTorch入门学习(九):神经网络-最大池化使用
目录 一、数据准备 二、创建神经网络模型 三、可视化最大池化效果 一、数据准备 首先,需要准备一个数据集来演示最大池化层的应用。在本例中,使用了CIFAR-10数据集,这是一个包含10个不同类别图像的数据集,用于分类任务。我们使…...
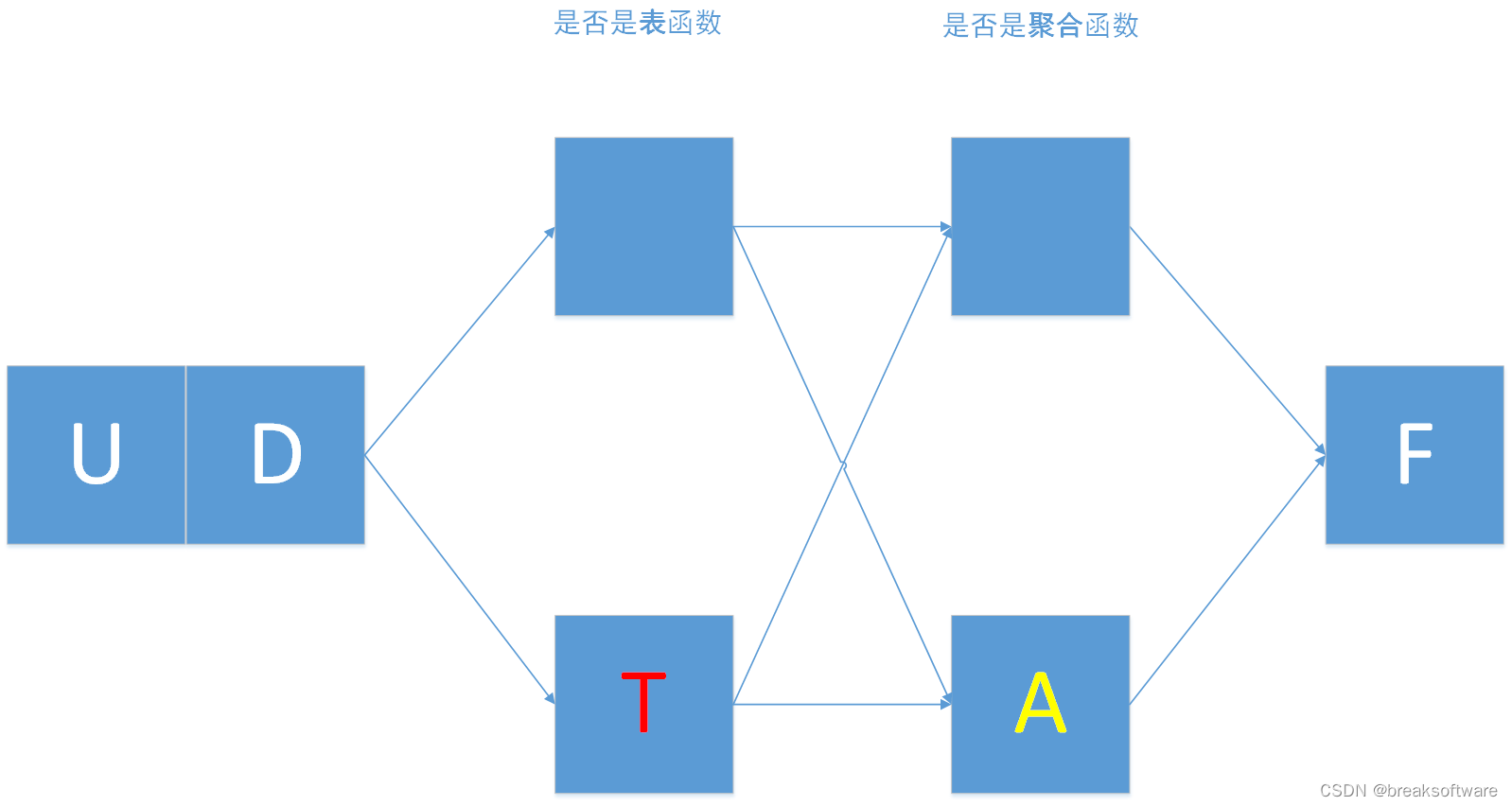
0基础学习PyFlink——用户自定义函数之UDF
大纲 标量函数入参并非表中一行(Row)入参是表中一行(Row)alias PyFlink中关于用户定义方法有: UDF:用户自定义函数。UDTF:用户自定义表值函数。UDAF:用户自定义聚合函数。UDTAF&…...

英语小作文模板(06求助+描述;07描述+建议)
06 求助描述: 题目背景及要求 第一段 第二段 第三段 翻译成中文 07 描述+建议: 题目背景及要求 第一段 第二段...

为什么感觉假期有时候比上班还累?
假期比上班还累的感觉可能由以下几个原因造成: 计划过度:在假期里,人们往往会制定各种计划,如旅游、聚会、休息等,以充分利用这段时间。然而,如果这些计划过于紧张或安排得过于紧密,就会导致身…...
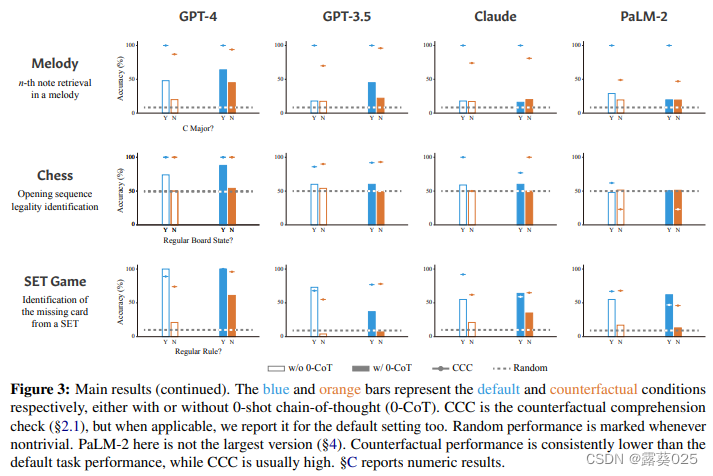
推理还是背诵?通过反事实任务探索语言模型的能力和局限性
推理还是背诵?通过反事实任务探索语言模型的能力和局限性 摘要1 引言2 反事实任务2.1 反事实理解检测 3 任务3.1 算术3.2 编程3.3 基本的句法推理3.4 带有一阶逻辑的自然语言推理3.5 空间推理3.6 绘图3.7 音乐3.8 国际象棋 4 结果5 分析5.1 反事实条件的“普遍性”5…...
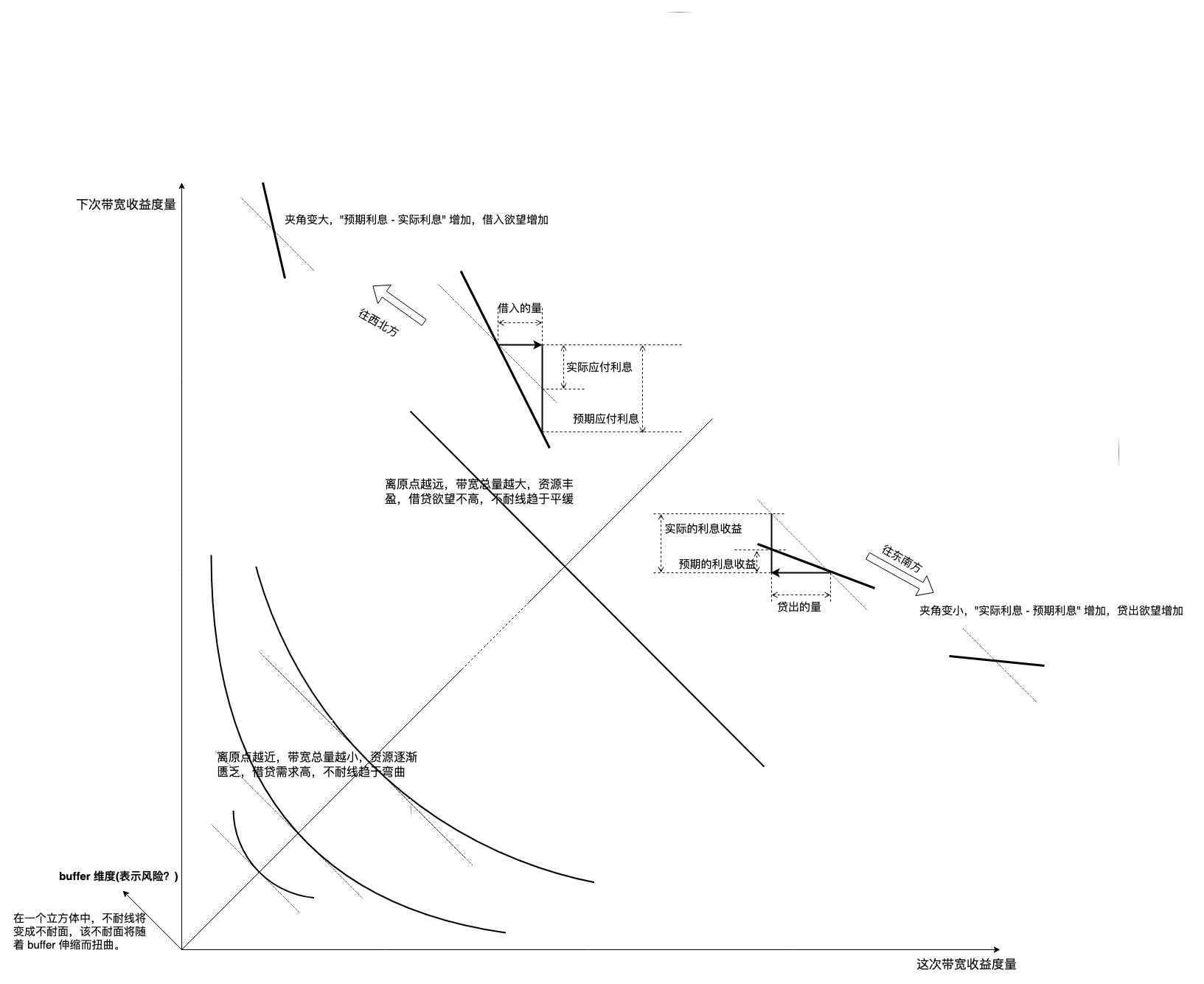
《利息理论》指导 TCP 拥塞控制
欧文费雪《利息原理》第 10 章,第 11 章对利息的几何说明是普适的,任何一个负反馈系统都能引申出新结论。给出原书图示,本文依据于此,详情参考原书: 将 burst 看作借贷是合理的,它包含成本(报文)…...
)
Bsdiff,Bspatch 的差分增量升级(基于Win和Linux)
目录 背景 内容 准备工作 在windows平台上 在linux平台上 正式工作 生成差分文件思路 作用差分文件思路 在保持相同目录结构进行差分增量升级 服务端(生成差分文件) 客户端(作用差分文件) 背景 像常见的Android 的linux平台,游戏,系统更新都…...

【3妹教我学历史-秦朝史】2 秦穆公-韩原之战
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 3妹:2哥,今天下班这么早&#…...

车载控制器
文章目录 车载控制器电动汽车上都有什么ECU 车载控制器 智能汽车上的控制器数量因车型和制造商而异。一般来说,现代汽车可能有50到100个电子控制单元(ECU)或控制器。这些控制器负责管理各种系统,如发动机管理、刹车、转向、空调、…...
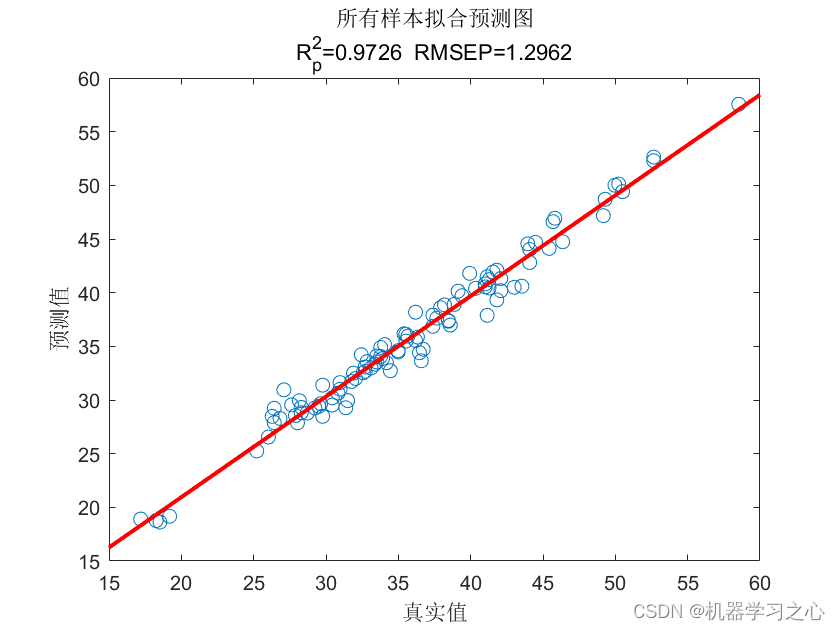
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 目录 回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.RIME-CNN-SVM霜冰优化算…...

使用Jaeger进行分布式跟踪:学习如何在服务网格中使用Jaeger来监控和分析请求的跟踪信息
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

添加多个单元对象
开发环境: Windows 11 家庭中文版Microsoft Visual Studio Community 2019VTK-9.3.0.rc0vtk-example参考代码 demo解决问题:不同阶段添加多个单元对象。 定义一个点集和一个单元集合,单元的类型可以是点、三角形、矩形、多边形等基本图形。只…...
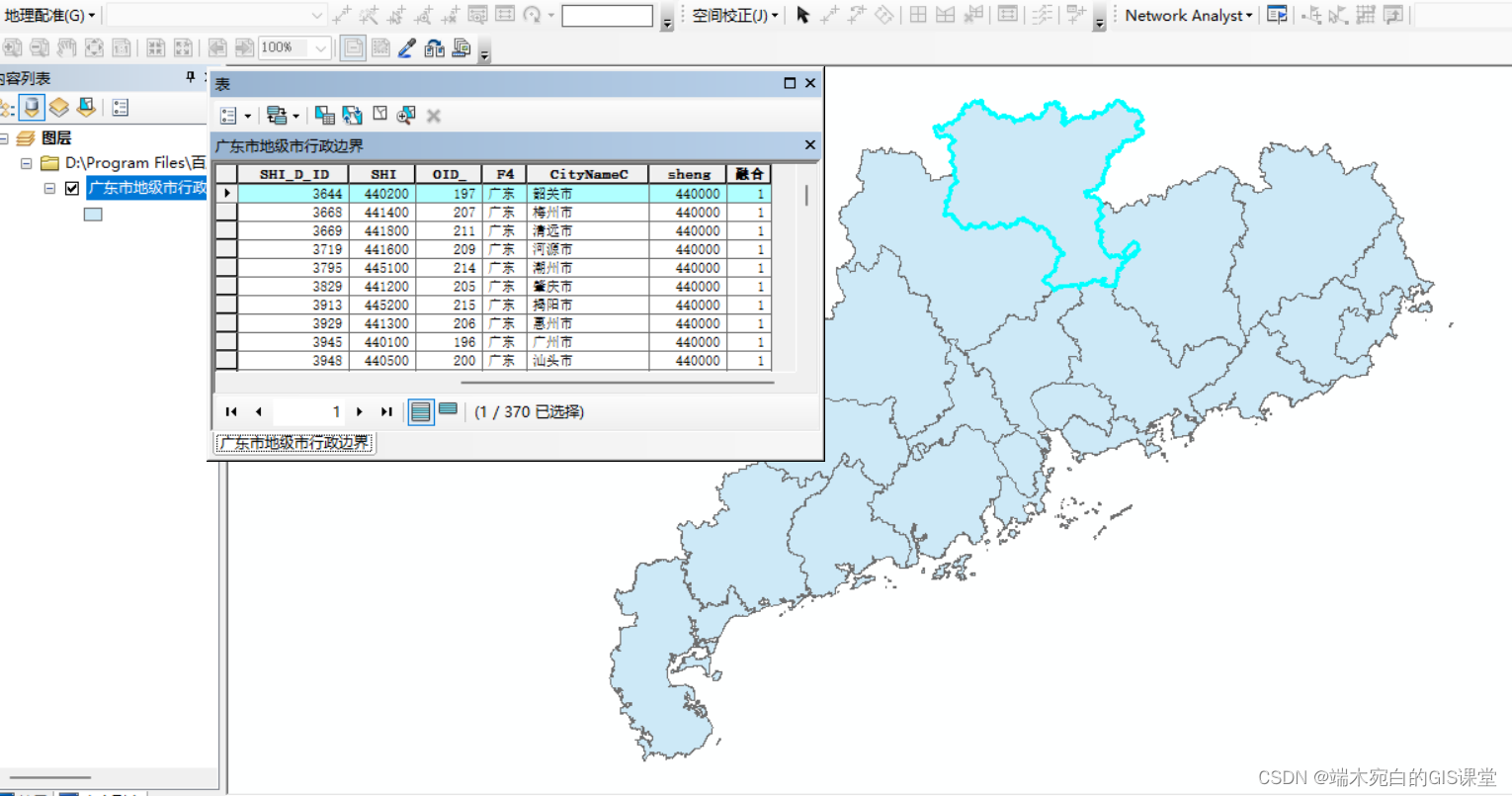
十八、模型构建器(ModelBuilder)快速提取城市建成区——批量掩膜提取夜光数据、夜光数据转面、面数据融合、要素转Excel(基于参考比较法)
一、前言 前文实现批量投影栅格、转为整型,接下来重点实现批量提取夜光数据,夜光数据转面、夜光数据面数据融合、要素转Excel。将相关结果转为Excel,接下来就是在Excel中进行阈值的确定,阈值确定无法通过批量操作,除非采用其他方式,但是那样的学习成本较高,对于参考比较…...

HarmonyOS开发:基于http开源一个网络请求库
前言 网络封装的目的,在于简洁,使用起来更加的方便,也易于我们进行相关动作的设置,如果,我们不封装,那么每次请求,就会重复大量的代码逻辑,如下代码,是官方给出的案例&am…...
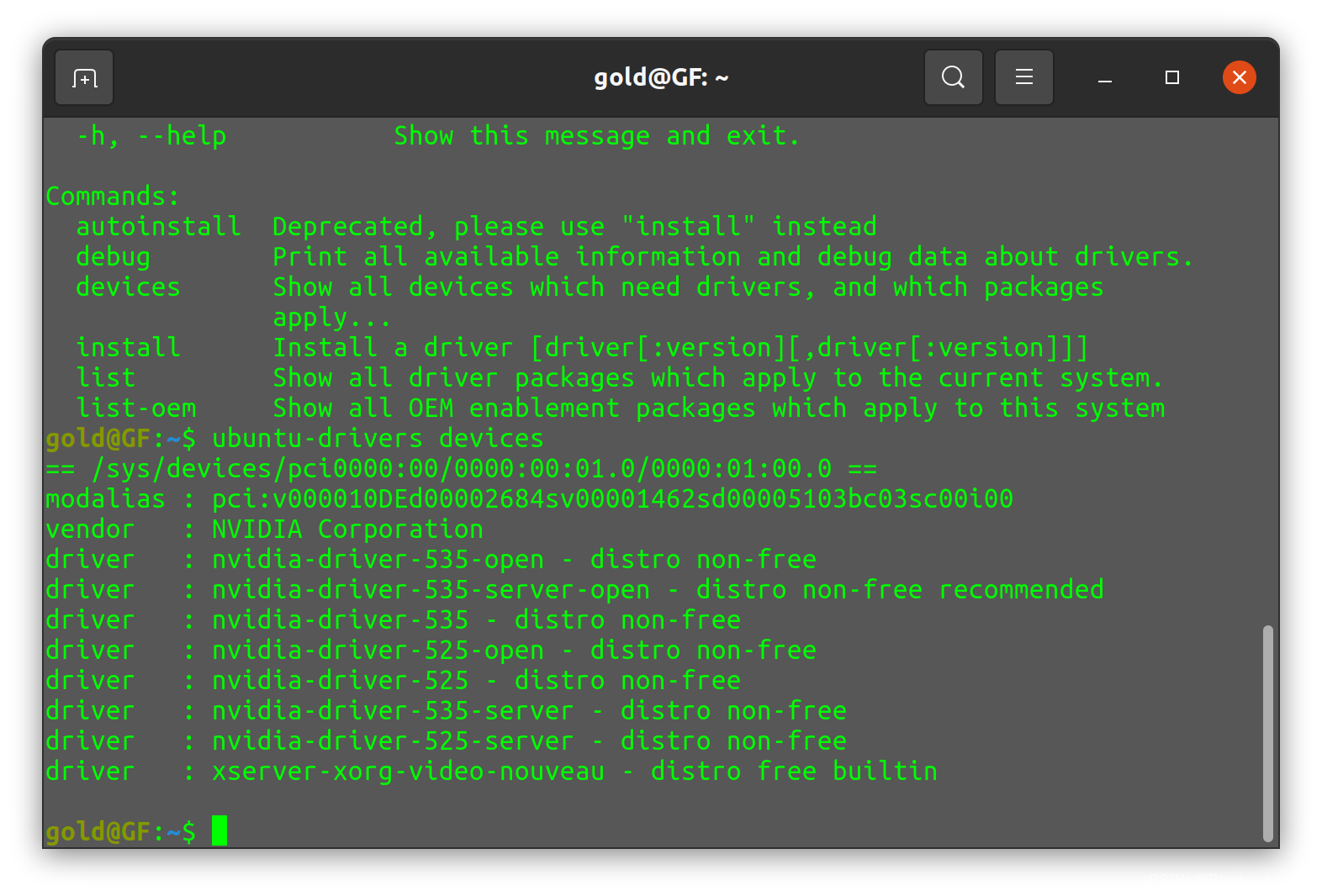
【杂记】Ubuntu20.04装系统,安装CUDA等
装20.04系统 安装系统的过程中,ROG的B660G主板,即使不关掉Secure boot也是可以的,不会影响正常安装,我这边出现问题的主要原因是使用了Ventoy制作的系统安装盘,导致每次一选择使用U盘的UEFI启动,就会跳回到…...

040-第三代软件开发-全新波形抓取算法
第三代软件开发-全新波形抓取算法 文章目录 第三代软件开发-全新波形抓取算法项目介绍全新波形抓取算法代码小解 关键字: Qt、 Qml、 抓波、 截获、 波形 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object …...
分享一个基于asp.net的供销社农产品商品销售系统的设计与实现(源码调试 lw开题报告ppt)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
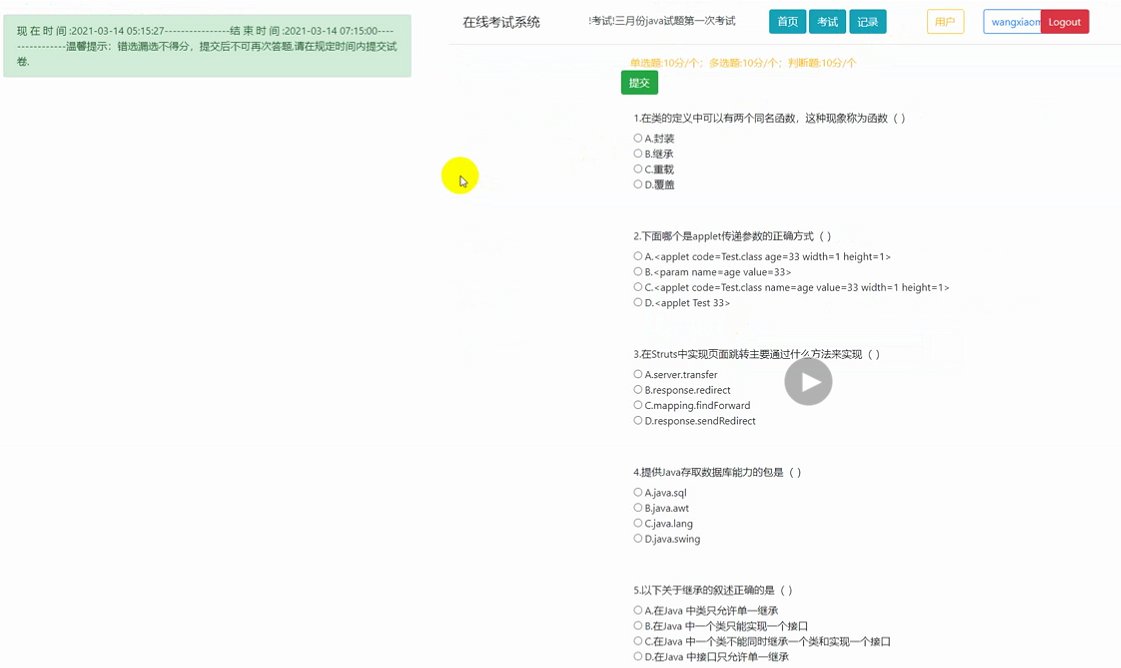
Java基于SpringBoot的线上考试系统
1 摘 要 基于 SpringBoot 的在线考试系统网站,功能模块具有课程管理、成绩管理、教师管理、学生管理、考试管理以及基本信息的管理等,通过将系统分为管理员、授课教师以及学生,从不同的身份角度来对用户提供便利,将科技与教学模式…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
