动手学深度学习(第二版)学习笔记 第三章
第三章 线性神经网络
代码:d2l-zh/pytorch/chapter_linear-networks
3.1 线性回归
3.1. 线性回归 — 动手学深度学习 2.0.0 documentation
解析解
线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解(analytical solution)。
首先,我们将偏置b合并到参数w中,合并方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化。
这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。
将损失关于∣∣y−Xw∣∣2||\bold y-\bold Xw||^2∣∣y−Xw∣∣2的导数设为0,得到解析解:
w∗=(XTX)−1XTy\bold w^*=(\bold X^T \bold X)^{-1} \bold X^T \bold y w∗=(XTX)−1XTy
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
随机梯度下降
算法的步骤如下: (1)初始化模型参数的值,如随机初始化; (2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
最优化方法一:梯度下降法_意念回复的博客-CSDN博客_梯度下降优化算法
矢量化加速
SIMD
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。 为了实现这一点,需要我们对计算进行矢量化, 从而利用线性代数库,而不是在Python中编写开销高昂的for循环。
%matplotlib inline
import math
import time
import numpy as np
import torchn = 10000
a = torch.ones([n])
b = torch.ones([n])c = torch.zeros(n)
timer = Timer()
for i in range(n):c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'
# '0.09661 sec'timer.start()
d = a + b
f'{timer.stop():.5f} sec'# '0.00021 sec'
结果很明显,第二种方法比第一种方法快得多。 矢量化代码通常会带来数量级的加速。 另外,我们将更多的数学运算放到库中,而无须自己编写那么多的计算,从而减少了出错的可能性。
3.2 线性回归的从零开始实验
3.2. 线性回归的从零开始实现 — 动手学深度学习 2.0.0 documentation
课后题
如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
谈谈神经网络权重为什么不能初始化为0
在单层网络中(一层线性回归层),将权重初始化为零时可以的,但是网络层数加深后,在全连接的情况下,在反向传播的时候,由于权重的对称性会导致出现隐藏神经元的对称性,使得多个隐藏神经元的作用就如同1个神经元,算法还是有效的,但是效果不大好。
3.3 线性回归的简洁实现
3.3. 线性回归的简洁实现 — 动手学深度学习 2.0.0 documentation
为什么机器学习优化算法都采取梯度下降(一阶导算法),而不采用牛顿法(二阶导算法),收敛速度更快,一般能算出一阶导, 二阶导也应该能算。
为什么机器学习中通常使用梯度下降进行训练
高阶导数信息的准确估计需要训练数据的批量更大
复杂高维神经网络的代价函数具有极多鞍点使高阶方法失效
其实核心还是神经网络参数数量大造成高阶方法计算、存储成本难以接受
如果样本大小不是批量数的整数倍,那需要随机剔除多余的样本吗?
如果是100个样本且batchsize=60 :
(1)就取剩下的40个(2)丢掉剩下的40个(3)从下一个epoch再补20个
3.4 softmax回归
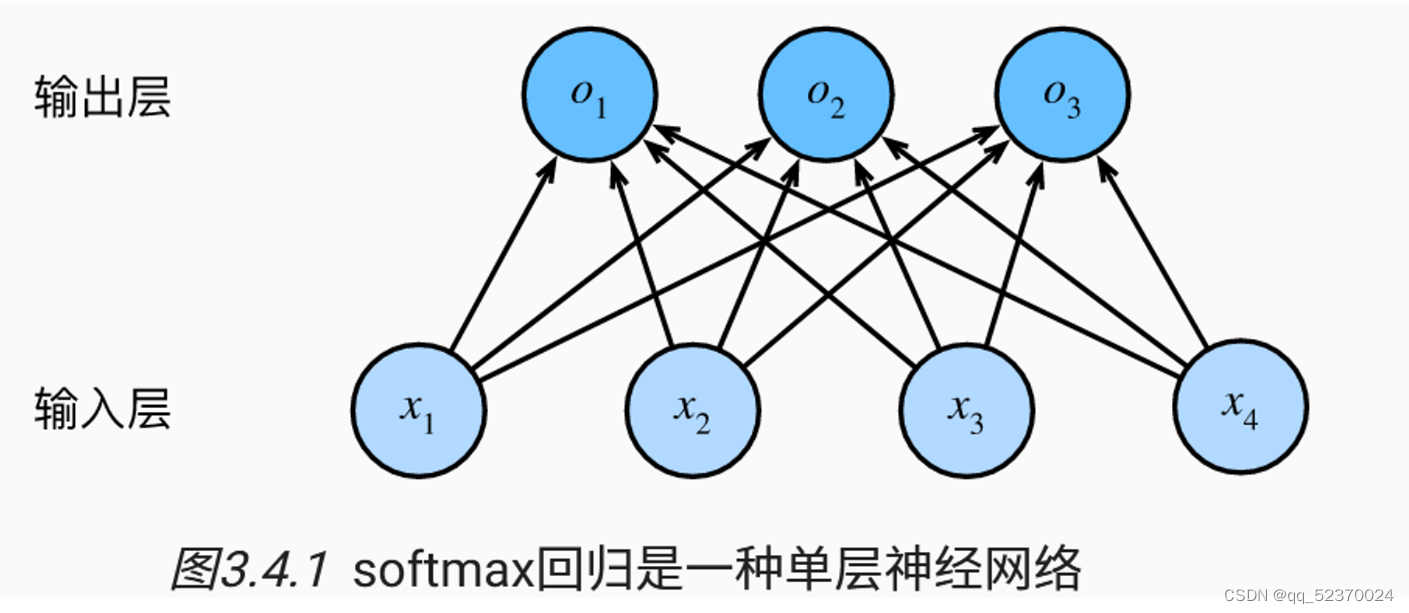
全连接层的参数开销
正如我们将在后续章节中看到的,在深度学习中,全连接层无处不在。 然而,顾名思义,全连接层是“完全”连接的,可能有很多可学习的参数。 具体来说,对于任何具有ddd个输入和qqq个输出的全连接层, 参数开销为O(dq)O(dq)O(dq),这个数字在实践中可能高得令人望而却步。 幸运的是,将ddd个输入转换为qqq个输出的成本可以减少到O(dqn)O(\frac{dq}{n})O(ndq), 其中超参数nnn可以由我们灵活指定,以在实际应用中平衡参数节约和模型有效性。
softmax运算

Huber’s Robust Loss
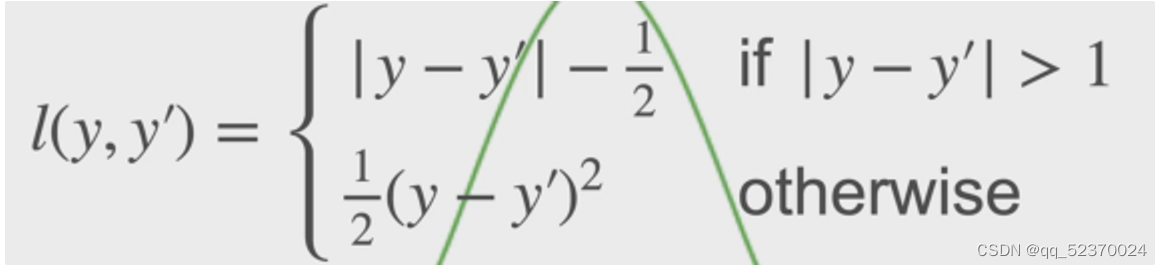
3.7 softmax回归的简洁实现
重新审视Softmax的实现

相关文章:

动手学深度学习(第二版)学习笔记 第三章
第三章 线性神经网络 代码:d2l-zh/pytorch/chapter_linear-networks 3.1 线性回归 3.1. 线性回归 — 动手学深度学习 2.0.0 documentation 解析解 线性回归的解可以用一个公式简单地表达出来,这类解叫作解析解(analytical solution&…...
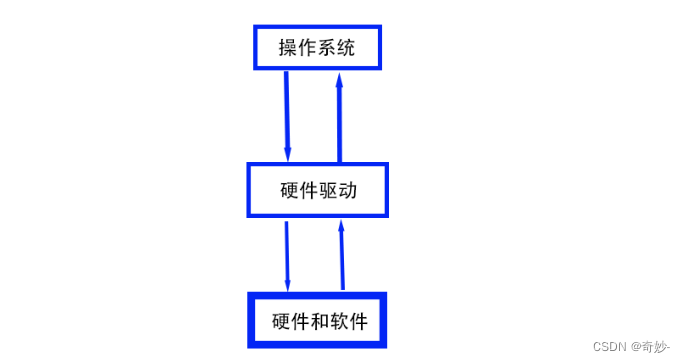
冯诺依曼体系结构与操作系统的概念及理解
一、 冯诺依曼体系结构1、概念2、内存的作用3、硬件原理解释软件行为二、操作系统的概念及基本作用1、概念2、设计操作系统的目的3、操作系统的主要作用4、什么是管理5、管理的目的6、操作系统如何为我们服务一、 冯诺依曼体系结构 我们常见的计算机,如笔记本。我们…...

【深度探讨】如何利用区块链改善公共服务
发表时间:2022年5月4日 信息来源:bsvblockchain.org BSV区块链协会全力支持符合企业和政府对于节能降耗和合法合规等相关要求的区块链生态系统。 然而,虽然监管机构负责其监管范围内的技术服务的性质、目的和影响,但他们并不是全…...

【打卡】图分析与节点嵌入
背景介绍 图(Graphs)是一种对物体(objects)和他们之间的关系(relationships)建模的数据结构,物体以结点(nodes)表示,关系以边(edges)…...
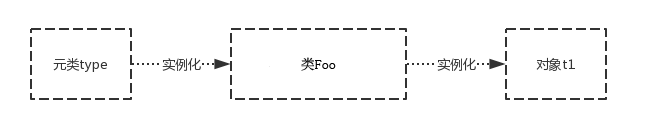
python元编程详解
什么是元编程 软件开发中很重要的一条原则就是“不要重复自己的工作(Don’t repeat youself)”,也就是说当我们需要复制粘贴代码时候,通常都需要寻找一个更加优雅的解决方案,在python中,这类问题常常会归类…...
为什么文档对 SaaS 公司至关重要?
在过去十年左右的时间里,SaaS的兴起使全球数百家公司成为家喻户晓的公司。但他们并不是仅仅依靠产品的力量到达那里的。客户服务和支持是使一切在幕后顺利进行的原因——其中很大一部分是文档。以正确的风格和正确的位置在您的网站上找到适当的用户文档对于将浏览器…...

Echarts 实现电池效果的柱状图
第022个点击查看专栏目录本示例是解决显示电池电量状态的柱状图,具体的核心代码请参考源代码。 文章目录示例效果示例源代码(共102行)相关资料参考专栏介绍示例效果 示例源代码(共102行) /* * Author: 还是大剑师兰特…...
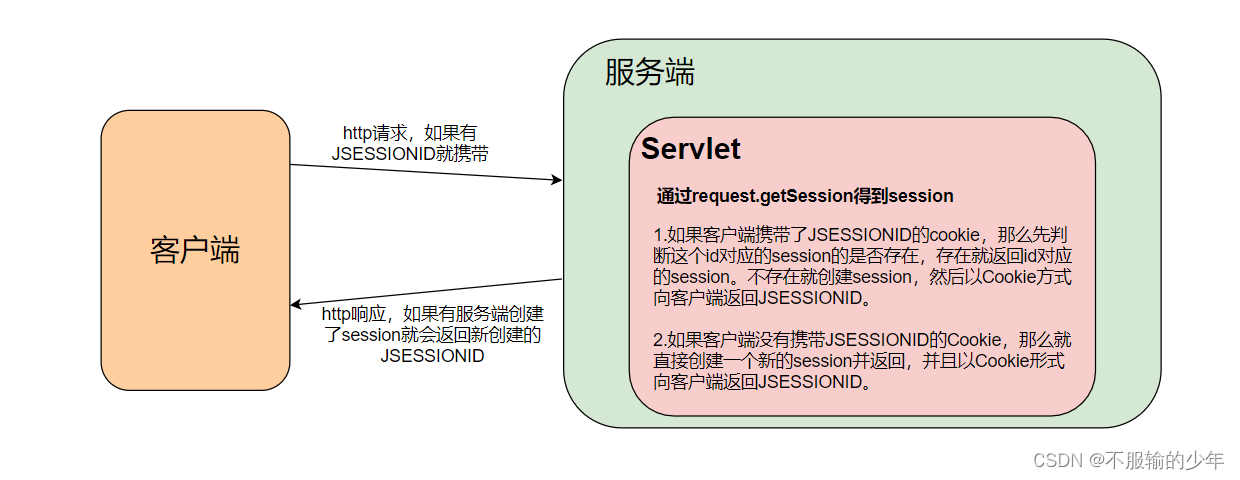
计算机网络高频知识点(一)
目录 一、http状态码 二、浏览器怎么数据缓存 三、强缓存与协商缓存 1、强缓存 2、协商缓存 四、简单请求与复杂请求 五、PUT 请求类型 六、GET请求类型 七、GET 和 POST 的区别 八、跨域 1、什么时候会跨域 2、解决方式 九、计算机网络的七层协议与五层协议分别指…...

JavaScript split()方法
JavaScript split()方法 目录JavaScript split()方法一、定义和用法二、语法三、参数值四、返回值五、更多实例5.1 省略分割参数5.2 使用limit参数5.3 使用一个字符作为分割符一、定义和用法 split() 方法用于把一个字符串分割成字符串数组。 二、语法 string.split(separat…...

前端面试题 —— 性能优化
目录 一、CDN的作用 二、CDN的使用场景 三、懒加载的概念 四、懒加载与预加载的区别 五、documentFragment 是什么?用它跟直接操作 DOM 的区别是什么? 六、常见的图片格式及使用场景 七、懒加载的特点 八、如何优化动画? 九、如何提⾼…...
我的周刊(第080期)
我的信息周刊,记录这周我看到的有价值的信息,主要针对计算机领域,内容主题极大程度被我个人喜好主导。这个项目核心目的在于记录让自己有印象的信息做一个留存以及共享。🎯 项目stable-diffusion-webui-docker[1]基于 Docker 的一…...
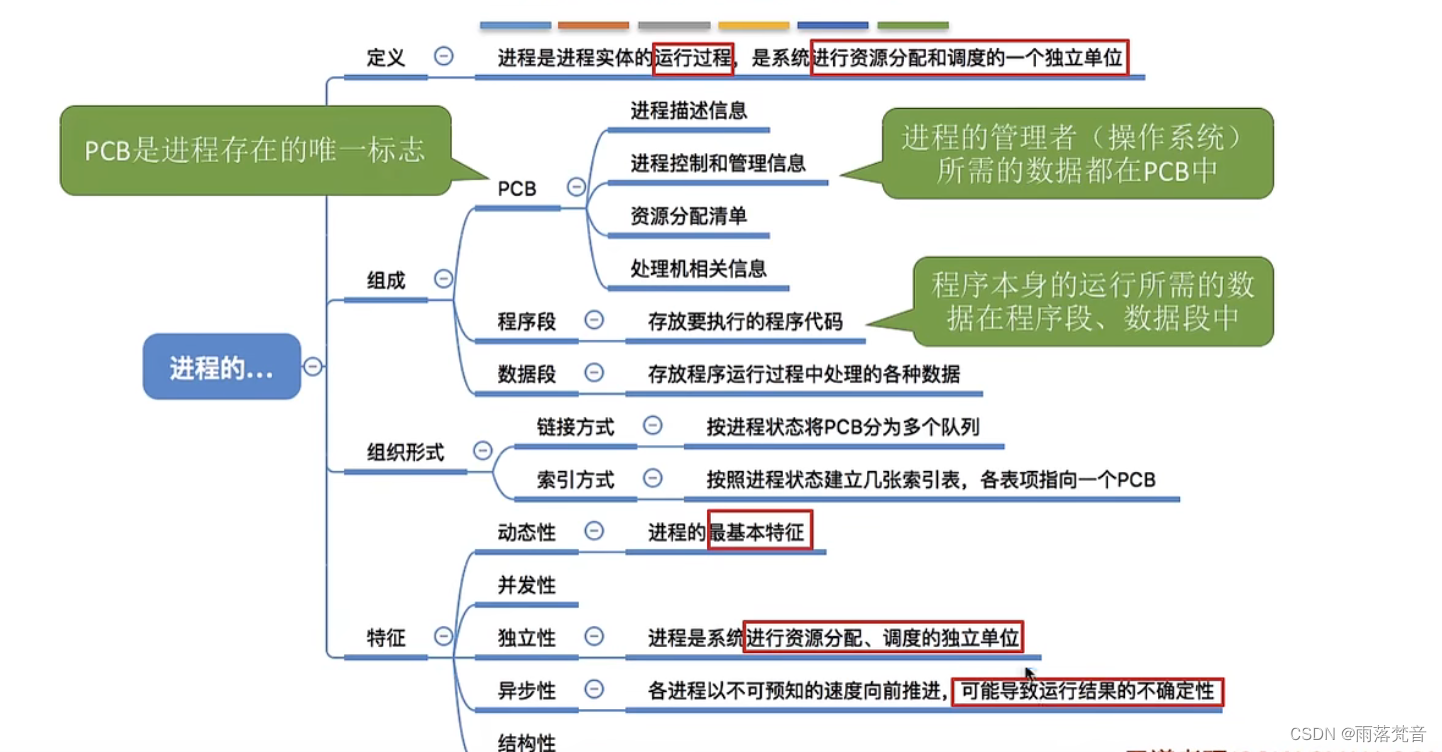
操作系统——7.进程的定义,组成,组成方式和特征
目录 1.概述 编辑2.定义 2.1单道程序 2.2多道程序 2.3进程定义 3.进程的组成 3.1进程的组成内容 3.2 PCB中的内容 4.进程的组织 4.1进程的两种组织方式 4.2链接方式 4.3索引方式 5.进程的特征 6.小结 这篇文章,我们主要来学习一下进程的定义࿰…...
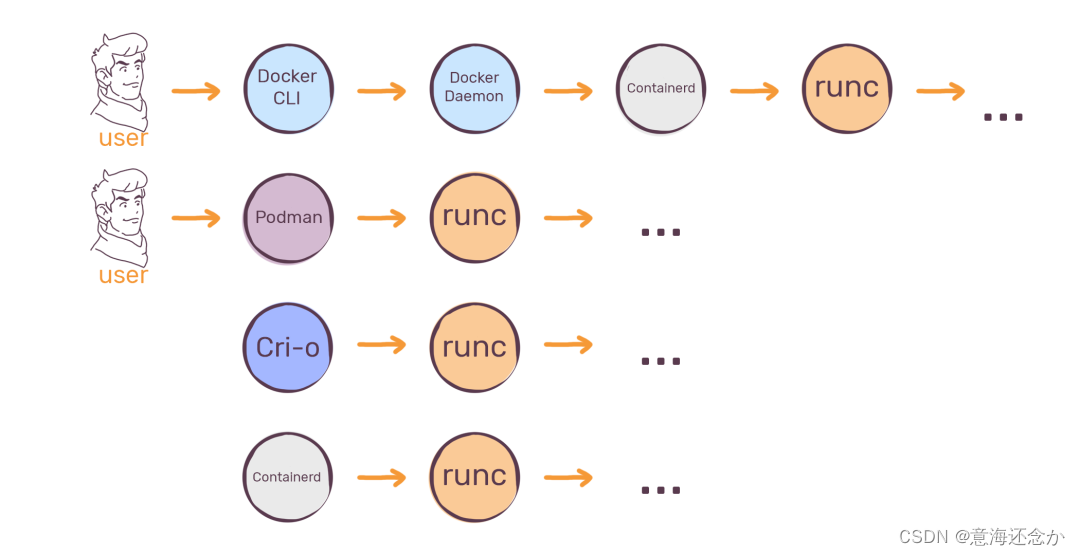
CRI-O, Containerd, Docker, Postman等概念介绍
参考:Docker,containerd,CRI,CRI-O,OCI,runc 分不清?看这一篇就够了Docker, containerd, CRI-O and runc之间的区别? Docker、Podman、Containerd 谁才是真正王者?CRI-O …...
【原创】java+swing+mysql设备预约管理系统设计与实现
我们在办公室或者学校实验室的,经常需要使用一些设备,因此需要提前租借。今天我们主要介绍如何使用javaswing和mysql数据库去完成一个设备预约管理系统,方便用户进行设备管理和预约。 功能分析: 设备预约管理系统主要是为了方便…...
Dashboard 安装)
7、kubernetes(k8s)Dashboard 安装
本文内容以语雀为准 说明 Kubernetes Dashboard 是一个通用的、基于Web的UI,用于Kubernetes集群管理。 它允许用户管理群集中运行的应用程序并对其进行故障排除,以及管理群集本身。 不同 Kubernetes Dashboard 支持的 Kubernetes 版本不同,…...

数学小课堂:虚数的媒介工具作用(虚构一个现实中不存在的概念,来解决现实问题)
文章目录 引言I 预备知识1.1 平方根1.2 三次方程1.3 极坐标II 虚数2.1 虚数的来源2.2 理解虚数存在的必要性2.3 虚数的影响III 复数3.1 人类认知升级的过程3.2 数字的扩展历史3.3 复数的用途引言 虚数的来源和存在的必要性:三次方程是一定有实数解的,因此根号里面负数的问题…...
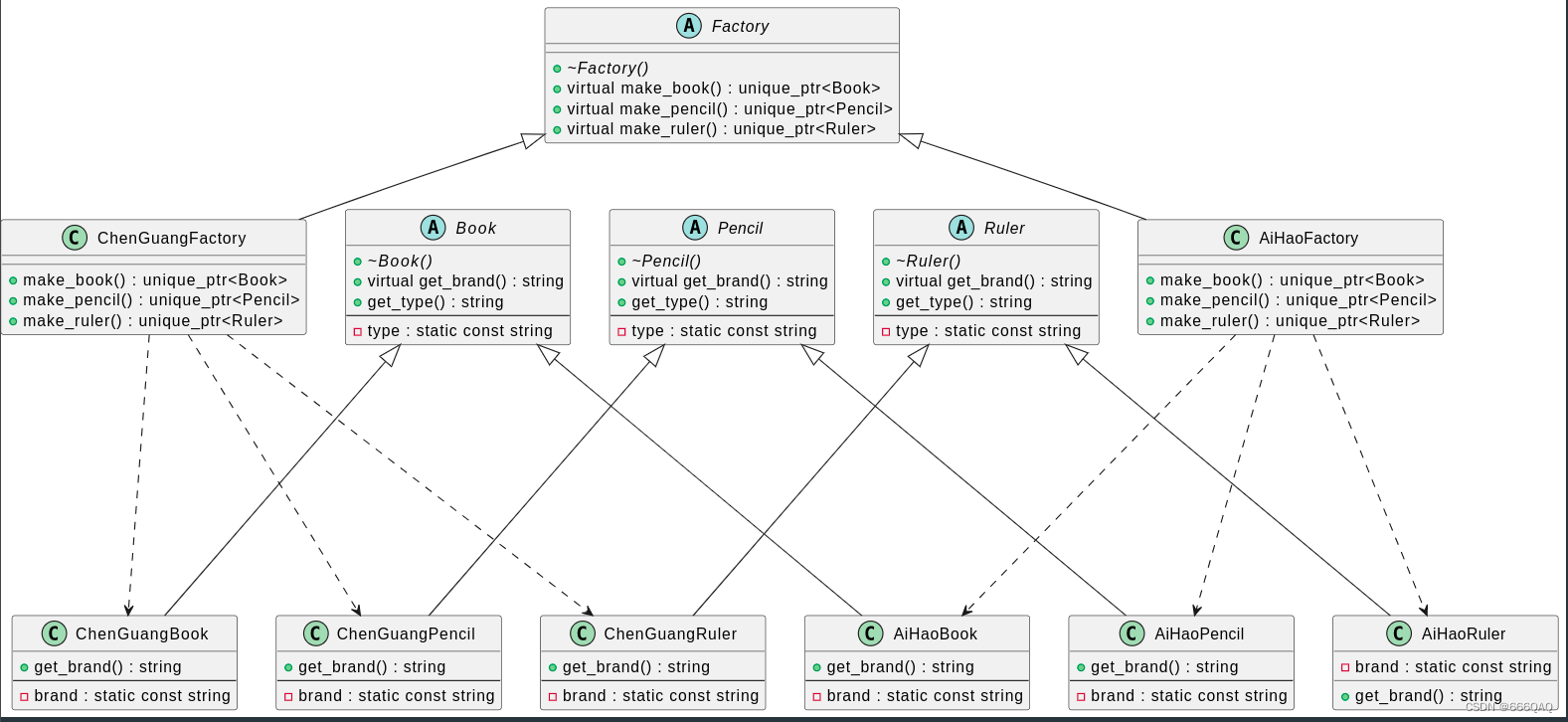
3.抽象工厂模式(Abstract Factory)
与工厂模式对比 工厂模式 工厂模式是类创建模式。在工厂模式中,只需要生产同一种产品,只不过是生产厂家不同。 所以产品类的设计: 抽象的产品类Product具体的产品类Product_A,Product_B, Product_C, Product_D…… 工厂的设计…...

synchronized底层如何实现?什么是锁的升级、降级?
第16讲 | synchronized底层如何实现?什么是锁的升级、降级? 我在上一讲对比和分析了 synchronized 和 ReentrantLock,算是专栏进入并发编程阶段的热身,相信你已经对线程安全,以及如何使用基本的同步机制有了基础&#…...
node环境搭建以及接口的封装
node环境搭建 文章目录node环境搭建1.在cmd中输入命令安装express(全局)2.在自己的项目下安装serve3.测试接口4.连接mysql4.1 创建数据表4.2 在serve目录下建db下的sql.js4.3 sql.js4.4 在serve路径下安装mysql4.5 在routes 中引入并发送请求4.6 请求到数…...
第七天)
跟着我从零开始入门FPGA(一周入门系列)第七天
7、设计一个只有4条指令的CPU我们要设计一个简单的CPU既然做CPU,我们要做流水线的,要简单,做2级流水线就够了。为了实例的简单,我们选择设计一个8bit的MCU的内核仍然我们要简单,所以选择RISC的内核,类似PIC…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
