三分/01分数规划
三分
最小球覆盖 2018南京D
三分套三分套三分
constexpr int N=105;
struct node{int x,y,z;
}a[N];
int n;
double road(double x1,double y1,double z1,double x2,double y2,double z2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)+(z1-z2)*(z1-z2));
}
double check(double x,double y,double z){double maxn=0;for (int i=1;i<=n;i++){maxn=std::max(maxn,road(x,y,z,a[i].x,a[i].y,a[i].z));}return maxn;
}
double check(double x,double y){double l=-100000,r=100000,ans=1e18;for (int i=1;i<=80;i++){double mid1=l+(r-l)/3,mid2=r-(r-l)/3;double res1=check(x,y,mid1),res2=check(x,y,mid2);if (res1<res2){r=mid2;}else{l=mid1;}ans=std::min(ans,std::min(res1,res2));}return ans;
}
double check(double x){double l=-100000,r=100000,ans=1e18;for (int i=1;i<=80;i++){double mid1=l+(r-l)/3,mid2=r-(r-l)/3;double res1=check(x,mid1),res2=check(x,mid2);if (res1<res2){r=mid2;}else{l=mid1;}ans=std::min(ans,std::min(res1,res2));}return ans;
}
void yrzr(){std::cin>>n;for (int i=1;i<=n;i++){std::cin>>a[i].x>>a[i].y>>a[i].z;}double l=-100000,r=100000,ans=1e18;for (int i=1;i<=80;i++){double mid1=l+(r-l)/3,mid2=r-(r-l)/3;// std::cout<<std::fixed<<std::setprecision(5)<<mid1<<" "<<mid2<<"\n";double res1=check(mid1),res2=check(mid2);if (res1<res2){r=mid2;}else{l=mid1;}ans=std::min(ans,std::min(res1,res2));}std::cout<<std::fixed<<std::setprecision(5)<<ans;
}
P2571 [SCOI2010] 传送带
感性理解一下,从 a b ab ab传送带到 c d cd cd传送带,每个传送带只有一个点出发/到达是最优的,所以单峰,满足三分性
int ax,ay,bx,by,cx,cy,dx,dy;
int p,q,r;
double road(double x1,double y1,double x2,double y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
double check(double x,double y){double lx=cx,ly=cy,rx=dx,ry=dy,ans=1e18;for (int i=1;i<=100;i++){double mid1x=(2*lx+rx)/3,mid1y=(2*ly+ry)/3;double mid2x=(lx+2*rx)/3,mid2y=(ly+2*ry)/3;double res1=road(dx,dy,mid1x,mid1y)/q+road(x,y,mid1x,mid1y)/r;double res2=road(dx,dy,mid2x,mid2y)/q+road(x,y,mid2x,mid2y)/r;if (res1>res2){lx=mid1x;ly=mid1y;}else{rx=mid2x;ry=mid2y;}ans=std::min(ans,res1);}return ans;
}
void yrzr(){std::cin>>ax>>ay>>bx>>by>>cx>>cy>>dx>>dy>>p>>q>>r;double lx=ax,ly=ay,rx=bx,ry=by,ans=1e18;for (int i=1;i<=100;i++){double mid1x=(2*lx+rx)/3,mid1y=(2*ly+ry)/3;double mid2x=(lx+2*rx)/3,mid2y=(ly+2*ry)/3;double res1=road(ax,ay,mid1x,mid1y)/p+check(mid1x,mid1y);double res2=road(ax,ay,mid2x,mid2y)/p+check(mid2x,mid2y);if (res1>res2){lx=mid1x;ly=mid1y;}else{rx=mid2x;ry=mid2y;}ans=std::min(ans,res1);}std::cout<<std::fixed<<std::setprecision(2)<<ans;
}
[SHOI2017]期末考试
从小到大排序,三分最后出成绩的时间,然后贪心,将晚出的学科进行操作
时间复杂度通过前缀和预处理可以做到 O ( n l o g n + l o g 2 n ) O(nlogn+log^2n) O(nlogn+log2n)
注意测试点C==1e16时会炸longlong,进行特判
constexpr int N=1e5+5;
int A,B,C,n,m;
int t[N],b[N],sum[N],tol[N];
int check(int dl){if (b[m]<=dl){return 0;}int pos=std::upper_bound(b+1,b+1+m,dl)-b;int sum1=dl*(pos-1)-tol[pos-1],sum2=(tol[m]-tol[pos-1])-(m-pos+1)*dl;if (B<=A){return sum2*B;}else{if (sum1>=sum2){return sum2*A;}else{return sum1*A+(sum2-sum1)*B;}}
}
void yrzr(){std::cin>>A>>B>>C>>n>>m;for (int i=1;i<=n;i++){std::cin>>t[i];}for (int i=1;i<=m;i++){std::cin>>b[i];}std::sort(t+1,t+1+n);for (int i=1;i<=n;i++){sum[i]=sum[i-1]+t[i];}std::sort(b+1,b+1+m);for (int i=1;i<=m;i++){tol[i]=tol[i-1]+b[i];}if (C==1e16){std::cout<<check(t[1]);return;}int ans=1e18;int l=0,r=100000,res1,res2;while (l<r){int mid1=(2*l+r)/3,mid2=(l+2*r)/3;int pos1=std::upper_bound(t+1,t+1+n,mid1)-t-1;int pos2=std::upper_bound(t+1,t+1+n,mid2)-t-1;res1=(mid1*pos1-sum[pos1])*C+check(mid1);res2=(mid2*pos2-sum[pos2])*C+check(mid2);if (res1>res2){l=mid1+1;}else{r=mid2-1;}ans=std::min(ans,std::min(res1,res2));// std::cout<<mid1<<" "<<res1<<" "<<mid2<<" "<<res2<<"\n";}std::cout<<ans;
}
分数规划
小咪买东西
板子
void yrzr(){int n,k;std::cin>>n>>k;std::vector<int> c(n+1),v(n+1);for (int i=1;i<=n;i++){std::cin>>c[i]>>v[i];}int l=0,r=1e9,ans=0;auto check=[&](int x){std::vector<int> temp;for (int i=1;i<=n;i++){temp.push_back(v[i]-c[i]*x);}std::sort(temp.begin(),temp.end(),[&](int i,int j){return i>j;});int sum=0;for (int i=0;i<k;i++){sum+=temp[i];}return (sum>=0?1:0);};while (l<=r){int mid=(l+r)>>1;if (check(mid)){l=mid+1;ans=mid;}else{r=mid-1;}}std::cout<<ans<<"\n";
}
gpa
转换一下,其实就是买的物品个数变成了一个范围 [ n − k , n ] [n-k,n] [n−k,n]
c h e c k check check的时候,一旦出现一个满足范围且 s u m > = 0 sum>=0 sum>=0的时候就是合法的
void yrzr(){int n,k;std::cin>>n>>k;std::vector<int> s(n+1),c(n+1);for (int i=1;i<=n;i++){std::cin>>s[i];}for (int i=1;i<=n;i++){std::cin>>c[i];c[i]*=s[i];}double l=0,r=1e9,ans=0;auto check=[&](double x){std::vector<double> temp;for (int i=1;i<=n;i++){temp.push_back(c[i]-x*s[i]);}std::sort(temp.begin(),temp.end(),[&](int i,int j){return i>j;});double sum=0;for (int i=1;i<=n;i++){sum+=temp[i-1];if (sum>0&&n-i<=k){return 1;}}return 0;};for (int i=1;i<=60;i++){double mid=(l+r)/2;if (check(mid)){l=mid+1;ans=mid;}else{r=mid-1;}}std::cout<<std::fixed<<std::setprecision(8)<<ans;
}
P4377 [USACO18OPEN] Talent Show G
与之前不同的是,此题没有限制选的数量,而是限制分母的和,二分完后,转换为背包问题即可
void yrzr(){int n,W;std::cin>>n>>W;std::vector<int> w(n+1),t(n+1);for (int i=1;i<=n;i++){std::cin>>w[i]>>t[i];t[i]*=1000;}int l=0,r=1e9,ans=0;auto check=[&](int x){std::vector<int> c(n+1),v(n+1);for (int i=1;i<=n;i++){c[i]=t[i]-w[i]*x;v[i]=w[i];}std::vector<int> f(W+1,-1e18);f[0]=0;for (int i=1;i<=n;i++){for (int j=W;j>=0;j--){f[std::min(W,j+v[i])]=std::max(f[std::min(W,j+v[i])],f[j]+c[i]);}}return (f[W]>=0?1:0);};while (l<=r){int mid=(l+r)/2;if (check(mid)){l=mid+1;ans=mid;}else{r=mid-1;}}std::cout<<ans<<"\n";
}
P4322 [JSOI2016] 最佳团体
二分答案,然后分数规划模型,转换一下发现就是重新定义每个人的点权,然后跑一个树上背包,但是树上背包要满足:儿子选了父亲一定要选
,特殊预处理一下即可
相关文章:

三分/01分数规划
三分 最小球覆盖 2018南京D 三分套三分套三分 constexpr int N105; struct node{int x,y,z; }a[N]; int n; double road(double x1,double y1,double z1,double x2,double y2,double z2){return sqrt((x1-x2)*(x1-x2)(y1-y2)*(y1-y2)(z1-z2)*(z1-z2)); } double check(double…...

大批卖家产品被下架!Temu又有新动作?
大批卖家产品被下架!Temu又有新动作? 近日,Temu正式上线韩国站,截止目前已上线27个国家地区。Temu海外市场发展迅猛,外界的声音也褒贬不一。这其中最有发言权的,应该就是Temu平台的卖家了! …...
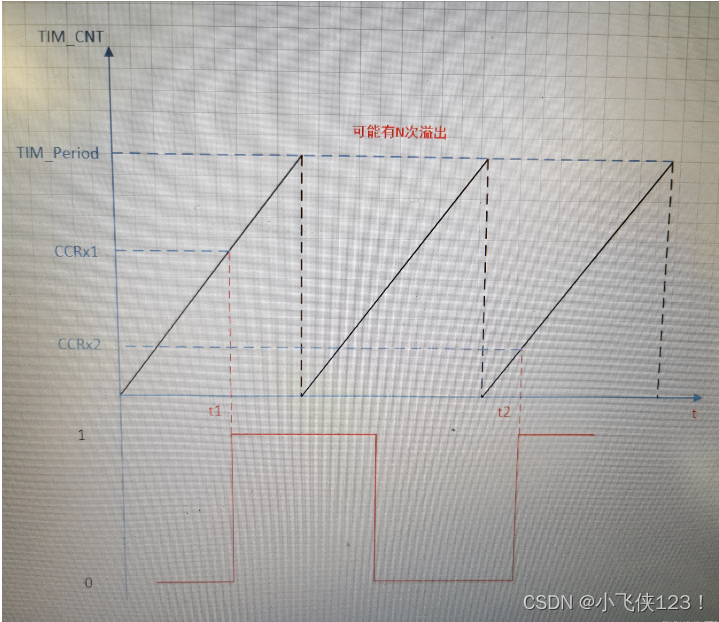
STM32 LL库 TIM3定时器多通道捕获输入采集
为什么不用HAL库,使用HAL库捕获输入一个通道还尚可,多通道捕获由于HAL的回调函数不符合我的要求,干脆直接切换到LL库。网上找了许多,代码处理写的不符合我的要求,这里记录一下我的调试过程。 TIM2输出1路PWM信号&#…...

如何为初创企业选择合适的 ERP 系统?
**ERP系统**是制造、分销、供应链、金融、会计、风险管理等多个行业必不可少的企业技术解决方案。不论垂直行业、企业规模或目标受众如何,将ERP作为企业管理战略的核心部分都非常重要。 对于渴望发展的小型企业和初创企业来说,更是如此。大型企业需要对…...

jssip contact的随机字符串的问题
let configuration {sockets: [socket],uri: sip:1001127.0.0.1,}; 如果这样注册freesswitch,那么fs注册信息中的Contact字段信息就是:sip:sdfsdfsdfsfcvdwvdwd.invalid;transportws;fs_natyes;fs_path... 正确的写法是: //URI是jssip内置…...

别再吐槽大学教材了,来看看这些网友强推的数学神作!
前言 关于大学数学教材的吐槽似乎从来没停止过。有人慨叹:数学教材晦涩难懂。错!难懂,起码还可以读懂。数学教材你根本读不懂;也有人说:数学教材简直就是天书。 数学教材有好有坏,这话不假,但更…...

Elasticsearch-汇总
Elasticsearch-基础介绍 跳转 分布式全文搜索引擎:包含【实时搜索】和【分析引擎】 Elasticsearch-倒排索引 跳转 倒排索引 跳转 Elasticsearch-Term Dictionary和Term Index 跳转 lucene-基础介绍 跳转 Elasticsearch-联合索引 跳转 Elasticsearch-Roaring B…...

9.3 【MySQL】系统表空间
了解完了独立表空间的基本结构,系统表空间的结构也就好理解多了,系统表空间的结构和独立表空间基本类似,只不过由于整个MySQL进程只有一个系统表空间,在系统表空间中会额外记录一些有关整个系统信息的页面,所以会比独立…...

STM32CUBEIDE生成hex文件 Release版本的下载不启动
现象描述: 使用STM32CUBEIDE生成hex文件,使用脱机下载器或者J-Flash下载到单片机中(STM32F407)单片机不启动。 测试其他的程序是可以启动的。 修改办法: 把Release版本切换到debug版本,重新编写…...

2023年亚太杯数学建模思路 - 复盘:校园消费行为分析
文章目录 0 赛题思路1 赛题背景2 分析目标3 数据说明4 数据预处理5 数据分析5.1 食堂就餐行为分析5.2 学生消费行为分析 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 赛题背景 校园一卡通是集…...

ceph集群移除物理节点
1. 概述 ceph分布式存储在生产或者实验环境,经常涉及到物理节点加入或者删除,本文仅对移除物理节点的相关步骤做了操作记录,以方便需要时查阅。 2. 移除物理节点 2.1 out掉相应osd 操作之前通过ceph -s确保整个集群状态是OK的,…...
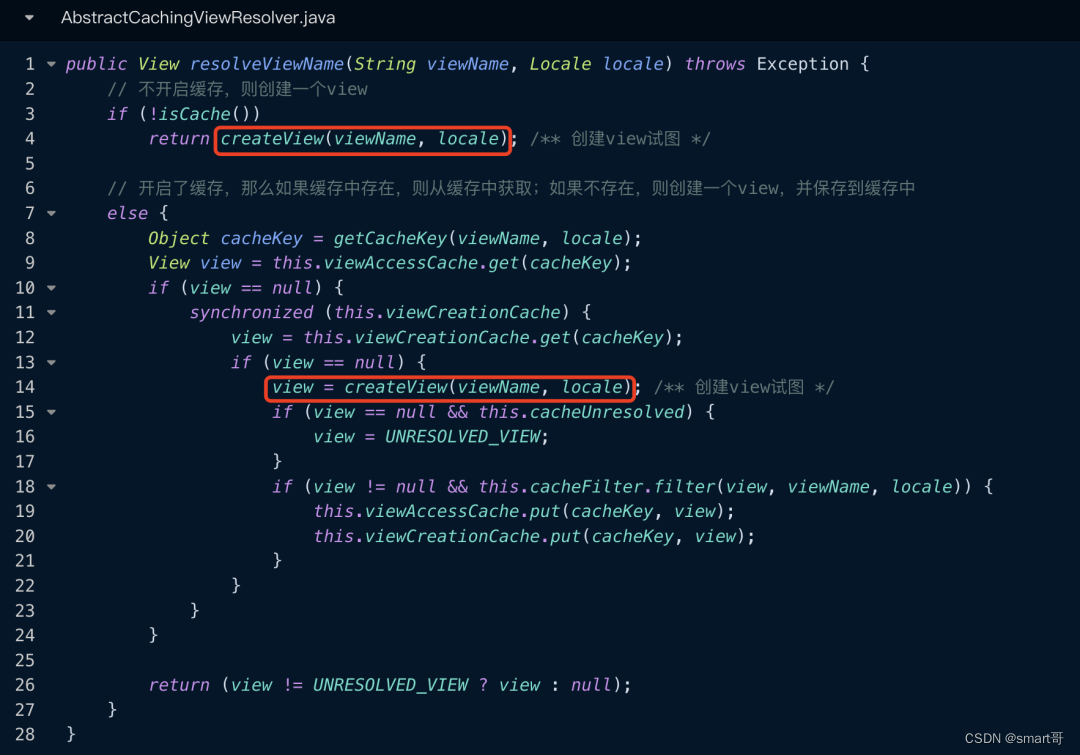
(八)Spring源码解析:Spring MVC
一、Servlet及上下文的初始化 1.1> DispatcherServlet的初始化 对于Spring MVC来说,最核心的一个类就是DispatcherServlet,它负责请求的行为流转。那么在Servlet的初始化阶段,会调用init()方法进行初始化操作,在DispatcherSe…...

maven或者gradle打完jar,jekins启动提示找不到问题
1、记录下遇到的一个问题,maven或者gradle打完jar,然后jekins发布,启动提示找不到实体类,mapper,xml问题 2、首先排查jar包中这些文件是否存在 3、然后排查每层的包名或者文件名是否能对应上 我这次遇到的问题就是本地…...

浏览器缓存sessionStorage、localStorage、Cookie
一、sessionStorage 1、简介 sessionStorage用于在浏览器会话期间存储数据,数据仅在当前会话期间有效。 存储的数据在用户关闭浏览器标签页或窗口后会被清除。 2、方法 使用sessionStorage.setItem(key, value)方法将数据存储在sessionStorage中。使用sessionSt…...

易点易动固定资产管理系统场景应用一:集成ERP/财务系统
在企业的日常运营中,固定资产管理是一个重要而繁琐的任务。传统的手工管理方式往往效率低下且容易出错,给企业带来不必要的成本和风险。为了解决这一问题,易点易动固定资产管理系统应运而生。本文将重点介绍易点易动固定资产管理系统在集成ER…...

k8s部署elk8 直接通过logstash获取日志文件方式
配置文件 kibana [rootnode101 config]# cat kibana.yml # # ** THIS IS AN AUTO-GENERATED FILE ** ## Default Kibana configuration for docker target server.host: "0.0.0.0" server.shutdownTimeout: "5s" elasticsearch.hosts: [ "http:/…...

git 本地多个账号错乱问题解决
当我们在本地有多个git账号时,例如公司的gitlab有一个git账号,自己的开源项目有一个GitHub账号,我们可能会出现账号错乱的情况,例如提交到公司gitlab的代码是github账号 这种情况通常是由于您的git config配置文件中的用户信息未…...

wu-ui-uniapp 多平台快速开发的UI框架
WU-UI 多平台快速开发的UI框架(无论平台,一致体验) 官方群 wu-ui官方1群: 767943089 说明 wu-ui(如虎添翼) 是 全面兼容多端的uniapp生态框架,基于vue2、vue3和nvue开发。丰富组件库,便捷工具库,简单高效。无论平台&#x…...
Spring Boot Actuator:自定义端点
要在Spring Boot Actuator中实现自定义端点,可以按照以下步骤进行操作: 1.创建一个自定义端点类 该类需要使用Endpoint注解进行标记,并使用Component注解将其作为Spring Bean进行管理。 package com.example.highactuator.point;import lo…...
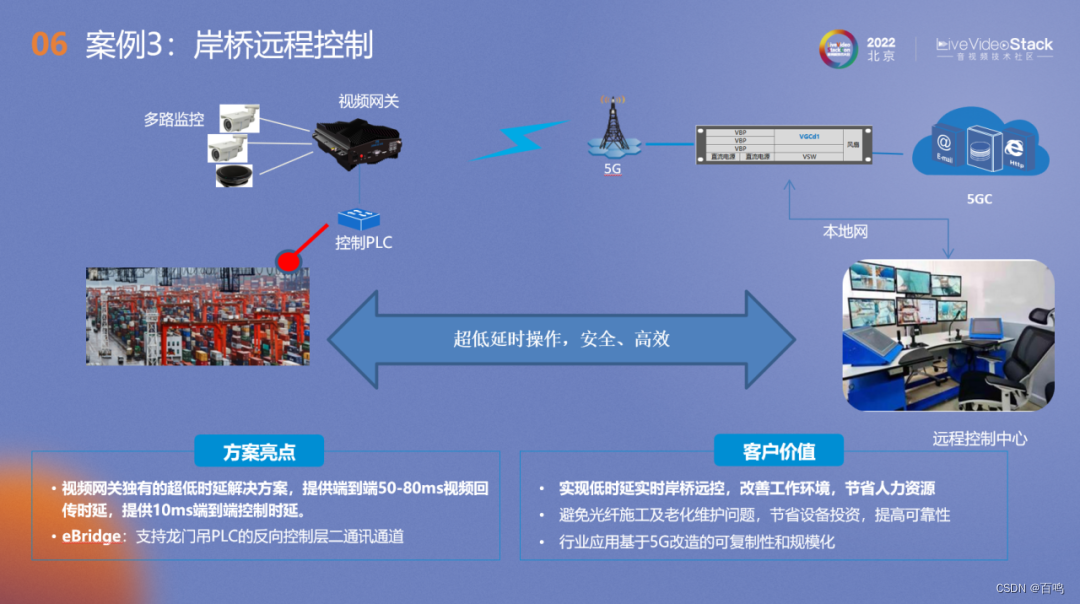
实时音视频方案汇总
若有好的方案欢迎留言讨论,非常感谢,汇总了一些,从市面上了解的一些低时延的端到端的方案,仅供参照,若有问题,也欢迎留言更正! 方案 方案描述 时延 备注 1大华同轴高清电缆200米电缆…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
