AM@幂级数性质@幂级数和函数求解
文章目录
- 幂级数性质
- 四则运算性质
- 分析性质
- 求解和函数
- 例
- 例
幂级数性质
- 和多项式有相似的性质
- 本文介绍用幂级数的性质求解幂级数和函数的两个例子
四则运算性质
-
若幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infin}a_{n}x^{n} ∑n=0∞anxn
(1)的收敛半径为 R 1 R_1 R1,和函数为 S 1 ( x ) S_1(x) S1(x)- 幂级数 ∑ n = 0 ∞ b n x n \sum_{n=0}^{\infin}b_{n}x^{n} ∑n=0∞bnxn
(2)的收敛半径为 R 2 R_2 R2,和函数为 S 2 ( x ) S_2(x) S2(x) - 令 R = min { R 1 , R 2 } R=\min\set{R_1,R_2} R=min{R1,R2}
- 幂级数 ∑ n = 0 ∞ b n x n \sum_{n=0}^{\infin}b_{n}x^{n} ∑n=0∞bnxn
-
则:
-
∑ n = 0 ∞ a n x n ± ∑ n = 0 ∞ b n x n \sum_{n=0}^{\infin}a_{n}x^{n}\pm{\sum_{n=0}^{\infin}b_{n}x^{n}} ∑n=0∞anxn±∑n=0∞bnxn= ∑ n = 0 ∞ ( a n ± b n ) x n \sum_{n=0}^{\infin}(a_{n}\pm{b_{n}})x^{n} ∑n=0∞(an±bn)xn= S 1 ( x ) ± S 1 ( x ) S_1(x)\pm{S_1(x)} S1(x)±S1(x),
(3)x ∈ ( − R , R ) x\in{(-R,R)} x∈(−R,R) -
( ∑ n = 0 ∞ a n x n ) ( ∑ n = 0 ∞ b n x n ) (\sum_{n=0}^{\infin}a_{n}x^{n})(\sum_{n=0}^{\infin}b_{n}x^{n}) (∑n=0∞anxn)(∑n=0∞bnxn)= ∑ n = 0 ∞ T n x n \sum_{n=0}^{\infin}{T_{n}}x^{n} ∑n=0∞Tnxn= S 1 ( x ) S 2 ( x ) S_1(x)S_2(x) S1(x)S2(x)
(4)- 多项式乘法中, n n n次项幂的系数表示为 a i b n − i a_{i}b_{n-i} aibn−i,其中 a i , b n − i a_{i},b_{n-i} ai,bn−i分别是 S 1 ( x ) S_1(x) S1(x), S 2 ( x ) S_2(x) S2(x)中的 i i i次项系数和 n − i n-i n−i次项系数
- a i x i b n − i x n − i a_{i}x^{i}b_{n-i}x^{n-i} aixibn−ixn−i= a i b n − i x n a_{i}b_{n-i}x^{n} aibn−ixn, i = 0 , 1 , 2 , ⋯ , n i=0,1,2,\cdots,n i=0,1,2,⋯,n
(5) - 若令 S 1 ( x ) S 2 ( x ) S_1(x)S_2(x) S1(x)S2(x)的 n n n次幂的系数为 T n T_n Tn,则 T n T_{n} Tn= ∑ i = 0 n a i b n − i \sum_{i=0}^{n}a_ib_{n-i} ∑i=0naibn−i
(6) - 因此式(4)为 ( ∑ n = 0 ∞ a n x n ) ( ∑ n = 0 ∞ b n x n ) (\sum_{n=0}^{\infin}a_{n}x^{n})(\sum_{n=0}^{\infin}b_{n}x^{n}) (∑n=0∞anxn)(∑n=0∞bnxn)= ∑ n = 0 ∞ ( ∑ i = 0 n a i b n − i ) x n \sum_{n=0}^{\infin}{(\sum_{i=0}^{n}a_ib_{n-i})}x^{n} ∑n=0∞(∑i=0naibn−i)xn
-
∑ n = 0 ∞ a n x n ∑ n = 0 ∞ b n x n \Large{\frac{\sum_{n=0}^{\infin}a_{n}x^{n}}{\sum_{n=0}^{\infin}b_{n}x^{n}}} ∑n=0∞bnxn∑n=0∞anxn= ∑ n = 0 ∞ c n x n \sum_{n=0}^{\infin}c_{n}x^{n} ∑n=0∞cnxn
(7)- 其中 c n c_{n} cn, n = 1 , 2 , ⋯ . n=1,2,\cdots. n=1,2,⋯.的确定比乘法中 T n T_{n} Tn的确定复杂一些
- 显然 ∑ n = 0 ∞ b n x n ⋅ ∑ n = 0 ∞ c n x n \sum_{n=0}^{\infin}b_{n}x^{n} \cdot \sum_{n=0}^{\infin}c_{n}x^{n} ∑n=0∞bnxn⋅∑n=0∞cnxn= ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infin}{a_{n}}x^{n} ∑n=0∞anxn
(8),而系数 c n c_n cn就是通过此方程式确定 - 由式(4)性质可知, Q n Q_{n} Qn= ∑ i = 0 n b i c n − i \sum_{i=0}^{n}b_ic_{n-i} ∑i=0nbicn−i,再比较式(8)两端系数,可知 a n a_{n} an= ∑ i = 0 n b i c n − i \sum_{i=0}^{n}b_ic_{n-i} ∑i=0nbicn−i
(9)- 分别令 n = 0 , 1 , 2 , ⋯ n=0,1,2,\cdots n=0,1,2,⋯可以从 ( 9 ) (9) (9)产生一系列方程
- a 0 a_0 a0= b 0 c 0 b_0c_{0} b0c0
- a 1 a_1 a1= b 0 c 1 + b 1 c 0 b_0c_{1}+b_{1}c_{0} b0c1+b1c0
- a 2 a_{2} a2= b 2 c 0 + b 1 c 1 + b 0 c 2 b_2c_0+b_1c_1+b_0c_2 b2c0+b1c1+b0c2
- ⋯ \cdots ⋯
- 依次求解方程组 n = 0 , 1 , 2 , ⋯ , k n=0,1,2,\cdots,k n=0,1,2,⋯,k的方程,即可依次求得 c 0 , c 1 , c 2 ⋯ c_0,c_1,c_{2}\cdots c0,c1,c2⋯
- 上述方法式递推法求解系数 c n c_n cn,如果要求 c k c_k ck,就要求阶 k k k个方程
- 分别令 n = 0 , 1 , 2 , ⋯ n=0,1,2,\cdots n=0,1,2,⋯可以从 ( 9 ) (9) (9)产生一系列方程
- 此时式(7)的收敛域可能比原来的两个级数的收敛域小得多
- 显然 ∑ n = 0 ∞ b n x n ⋅ ∑ n = 0 ∞ c n x n \sum_{n=0}^{\infin}b_{n}x^{n} \cdot \sum_{n=0}^{\infin}c_{n}x^{n} ∑n=0∞bnxn⋅∑n=0∞cnxn= ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infin}{a_{n}}x^{n} ∑n=0∞anxn
- 其中 c n c_{n} cn, n = 1 , 2 , ⋯ . n=1,2,\cdots. n=1,2,⋯.的确定比乘法中 T n T_{n} Tn的确定复杂一些
-
分析性质
-
和多项式类似的分项积分和分项求导性质,并且不改变收敛区间
-
设幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infin}a_{n}x^{n} ∑n=0∞anxn的和函数为 s ( x ) s(x) s(x),收敛域为 I I I
-
s ( x ) s(x) s(x)在 I I I上连续
-
s ( x ) s(x) s(x)在 I I I上可积,且有逐项积分公式(变上限积分): ∫ 0 x s ( t ) d t \int_{0}^{x}s(t)\mathrm{d}t ∫0xs(t)dt= ∫ 0 x [ ∑ n = 0 ∞ a n t n ] d t \int_{0}^{x}[\sum_{n=0}^{\infin}a_{n}t^{n}]\mathrm{d}t ∫0x[∑n=0∞antn]dt= ∑ n = 0 ∞ ∫ 0 x a n t n d t \sum_{n=0}^{\infin}\int_{0}^{x}a_{n}t^{n}\mathrm{d}t ∑n=0∞∫0xantndt= ∑ n = 0 ∞ a n n + 1 x n + 1 \sum_{n=0}^{\infin}\frac{a_{n}}{n+1}{x^{n+1}} ∑n=0∞n+1anxn+1, ( x ∈ I ) (x\in{I}) (x∈I)
- 积分区间为 [ 0 , x ] [0,x] [0,x]
- 逐项积分后,所得的幂级数和原级数有相同的收敛半径
-
s ( x ) s(x) s(x)在 ( − R , R ) (-R,R) (−R,R)内可导,且有逐项求导公式 s ′ ( x ) s'(x) s′(x)= ( ∑ n = 0 ∞ a n x n ) ′ (\sum_{n=0}^{\infin}a_{n}x^{n})' (∑n=0∞anxn)′= ∑ n = 0 ∞ ( a n x n ) ′ \sum_{n=0}^{\infin}(a_{n}x^{n})' ∑n=0∞(anxn)′= ∑ n = 0 ∞ n a n x n − 1 \sum_{n=0}^{\infin}na_{n}x^{n-1} ∑n=0∞nanxn−1, ( ∣ x ∣ < R ) (|x|<R) (∣x∣<R)
-
逐项求导后所得的幂级数和原级数有相同的收敛半径
-
注意,虽然收敛半径相同,但是收敛域不一定相同,求导可能收敛域对应得端点处不再收敛
-
例如原幂级数的收敛域为 [ − R , R ) [-R,R) [−R,R),那么求导后的半径变为 ( − R , R ) (-R,R) (−R,R),显然两个区间不相等;但如果原幂级数的收敛域为 ( − R , R ) (-R,R) (−R,R),那么求导后的级数收敛域不变
-
反复应用上述结论可知, s ( x ) s(x) s(x)在其**收敛区间 ( − R , R ) (-R,R) (−R,R)**内具有任意阶导数
-
-
求解和函数
- 分析性质可以用于求解幂级数的和函数,也就是幂级数收敛于什么函数 s ( x ) s(x) s(x)
- 第一步就是要求解收敛域,这时和函数的定义域
- 求出收敛半径 R R R
- 再检验 x = ± R x=\pm{R} x=±R是的敛散性,以确定收敛域
例
- 求 ∑ n = 0 ∞ x n n + 1 \sum_{n=0}^{\infin}\frac{x^{n}}{n+1} ∑n=0∞n+1xn的收敛域以及和函数 s ( x ) s(x) s(x)
- (1)
- 判断级数类型:该级数是一个幂级数,并且是标准形
- 确定通项的系数: a n a_n an= 1 n + 1 \frac{1}{n+1} n+11
- 观察 a n a_{n} an考虑使用比值式考察其是否收敛(敛散性),
- ρ \rho ρ= lim n → ∞ n + 1 n + 2 \lim\limits_{n\to\infin}\frac{n+1}{n+2} n→∞limn+2n+1= 1 1 1, R = 1 ρ R=\frac{1}{\rho} R=ρ1=1
- 说明原级数收敛,且收敛半径为 R = 1 R=1 R=1,收敛区间就是 ( − 1 , 1 ) (-1,1) (−1,1)
- 考察区间端点处,对应的常数项级数:
- x = − 1 x=-1 x=−1时,通项为 ( − 1 ) n n + 1 \frac{(-1)^{n}}{n+1} n+1(−1)n,对应的常数项级数为 ∑ n = 0 ∞ ( − 1 ) n n + 1 \sum_{n=0}^{\infin}\frac{(-1)^{n}}{n+1} ∑n=0∞n+1(−1)n= 1 − 1 2 + ⋯ 1-\frac{1}{2}+\cdots 1−21+⋯
- 这时一个交错级数,由Leibniz定理, 1 n + 1 \frac{1}{n+1} n+11递减,且 1 n + 1 → 0 ( n → ∞ ) \frac{1}{n+1}\to{0}(n\to{\infin}) n+11→0(n→∞)
- 可知该级数收敛
- x = 1 x=1 x=1时,幂级数称为 ∑ n = 0 ∞ 1 n + 1 \sum_{n=0}^{\infin}\frac{1}{n+1} ∑n=0∞n+11= ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infin}\frac{1}{n} ∑n=1∞n1,是调和级数,其显然是发散的
- 综上,收敛域为 I = [ − 1 , 1 ) I=[-1,1) I=[−1,1)
- x = − 1 x=-1 x=−1时,通项为 ( − 1 ) n n + 1 \frac{(-1)^{n}}{n+1} n+1(−1)n,对应的常数项级数为 ∑ n = 0 ∞ ( − 1 ) n n + 1 \sum_{n=0}^{\infin}\frac{(-1)^{n}}{n+1} ∑n=0∞n+1(−1)n= 1 − 1 2 + ⋯ 1-\frac{1}{2}+\cdots 1−21+⋯
- (2)
- 求 s ( x ) s(x) s(x)就是在收敛域内,要将级数形式化简为非求和形式
- 令 s ( x ) s(x) s(x)= ∑ n = 0 ∞ x n n + 1 \sum_{n=0}^{\infin}\frac{x^{n}}{n+1} ∑n=0∞n+1xn
(1), x ∈ [ − 1 , 1 ) x\in[-1,1) x∈[−1,1)- 式(1)两边同时乘以 x x x, x s ( x ) xs(x) xs(x)= ∑ n = 0 ∞ x n + 1 n + 1 \sum_{n=0}^{\infin}\frac{x^{n+1}}{n+1} ∑n=0∞n+1xn+1= ∑ n = 1 ∞ x n n \sum_{n=1}^{\infin}\frac{x^{n}}{n} ∑n=1∞nxn
(2), x ∈ [ − 1 , 1 ) x\in[-1,1) x∈[−1,1) - 对(2)两边求导,并由逐项求导公式,得 ( x s ( x ) ) ′ (xs(x))' (xs(x))′= ∑ n = 1 ∞ x n − 1 \sum_{n=1}^{\infin}{x^{n-1}} ∑n=1∞xn−1= 1 + x + x 2 + ⋯ + x n + ⋯ 1+x+x^2+\cdots+x^{n}+\cdots 1+x+x2+⋯+xn+⋯, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
(3)- Note:求导后收敛区间为 ∣ x ∣ < 1 |x|<1 ∣x∣<1,即 x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 而我们知道常用级数 1 1 − x \frac{1}{1-x} 1−x1= 1 + x + x 2 + ⋯ + x n + ⋯ 1+x+x^2+\cdots+x^{n}+\cdots 1+x+x2+⋯+xn+⋯, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
(4) - 比较(3,4)可得 ( x s ( x ) ) ′ (xs(x))' (xs(x))′= 1 1 − x \frac{1}{1-x} 1−x1, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
(5)- 对上式从 0 0 0到 x x x积分,得 x s ( x ) xs(x) xs(x)= ∫ 0 x 1 1 − t d t \int_{0}^{x}\frac{1}{1-t}\mathrm{d}t ∫0x1−t1dt= − ln ∣ t − 1 ∣ ∣ 0 x -\ln|t-1||_{0}^{x} −ln∣t−1∣∣0x= − ln ∣ x − 1 ∣ -\ln|x-1| −ln∣x−1∣
(6), x ∈ [ − 1 , 1 ) x\in[-1,1) x∈[−1,1)
- 对上式从 0 0 0到 x x x积分,得 x s ( x ) xs(x) xs(x)= ∫ 0 x 1 1 − t d t \int_{0}^{x}\frac{1}{1-t}\mathrm{d}t ∫0x1−t1dt= − ln ∣ t − 1 ∣ ∣ 0 x -\ln|t-1||_{0}^{x} −ln∣t−1∣∣0x= − ln ∣ x − 1 ∣ -\ln|x-1| −ln∣x−1∣
- 方法2:
- 这里可以不处理为 x s ( x ) xs(x) xs(x),而直接变形为: s ( x ) s(x) s(x)= 1 x ∑ n = 0 ∞ x n + 1 n + 1 \frac{1}{x}\sum_{n=0}^{\infin}\frac{x^{n+1}}{n+1} x1∑n=0∞n+1xn+1= 1 x ∑ n = 0 ∞ ∫ 0 n t n d t \frac{1}{x}\sum_{n=0}^{\infin}\int_{0}^{n}t^{n}\mathrm{d}t x1∑n=0∞∫0ntndt= 1 x ∫ 0 n ( ∑ n = 0 ∞ t n ) d t \frac{1}{x}\int_{0}^{n}(\sum_{n=0}^{\infin}t^{n})\mathrm{d}t x1∫0n(∑n=0∞tn)dt
- 再利用常用已知级数 ∑ n = 0 ∞ t n \sum_{n=0}^{\infin}t^{n} ∑n=0∞tn= 1 1 − t \frac{1}{1-t} 1−t1, t ∈ ( − 1 , 1 ) t\in(-1,1) t∈(−1,1),得 s ( x ) s(x) s(x)= 1 x ∫ 0 n ( 1 1 − t ) d t \frac{1}{x}\int_{0}^{n}(\frac{1}{1-t})\mathrm{d}t x1∫0n(1−t1)dt,同样得到式(6)
- 当 x ≠ 0 x\neq{0} x=0时,有 s ( x ) s(x) s(x)= − 1 x ln ( 1 − x ) -\frac{1}{x}\ln(1-x) −x1ln(1−x)
(7) - 当 x = 0 x=0 x=0,
- s ( 0 ) = a 0 = 1 s(0)=a_{0}=1 s(0)=a0=1
- ∑ n = 0 ∞ 0 n n + 1 \sum_{n=0}^{\infin}\frac{0^{n}}{n+1} ∑n=0∞n+10n= 0 0 0 + 1 \frac{0^{0}}{0+1} 0+100+ ∑ n = 1 ∞ 0 n n + 1 \sum_{n=1}^{\infin}\frac{0^{n}}{n+1} ∑n=1∞n+10n= 1 + 0 1+0 1+0= 1 1 1,这里约定 0 0 = 1 0^{0}=1 00=1
- 或者也可以由 s ( x ) s(x) s(x)是连续的性质可以由极限式 lim x → 0 ( − 1 x ln ( 1 − x ) ) \lim\limits_{x\to{0}}(-\frac{1}{x}\ln(1-x)) x→0lim(−x1ln(1−x))= lim x → 0 ( − − x x ) \lim\limits_{x\to{0}}(-\frac{-x}{x}) x→0lim(−x−x)=1,从而 s ( 0 ) s(0) s(0)=1
- ln ( 1 − x ) ∼ − x \ln(1-x)\sim{-x} ln(1−x)∼−x, ( − x → 0 ) (-x\to{0}) (−x→0)
- 或者洛必达法则计算
- s ( 0 ) = a 0 = 1 s(0)=a_{0}=1 s(0)=a0=1
- 式(1)两边同时乘以 x x x, x s ( x ) xs(x) xs(x)= ∑ n = 0 ∞ x n + 1 n + 1 \sum_{n=0}^{\infin}\frac{x^{n+1}}{n+1} ∑n=0∞n+1xn+1= ∑ n = 1 ∞ x n n \sum_{n=1}^{\infin}\frac{x^{n}}{n} ∑n=1∞nxn
例
- 令 u n u_{n} un= ( − 1 ) n − 1 n x n − 1 (-1)^{n-1}nx^{n-1} (−1)n−1nxn−1,求幂级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infin} u_{n} ∑n=1∞un的和函数
- (1)求收敛半径
- 方法1:
- ∣ u n ∣ |u_{n}| ∣un∣= ∣ n x n − 1 ∣ |nx^{n-1}| ∣nxn−1∣, ∣ u n ∣ n \sqrt[n]{|u_{n}|} n∣un∣= ∣ x ∣ n x − 1 n |x|\sqrt[n]{nx^{-1}} ∣x∣nnx−1
- lim n → ∞ u n n \lim\limits_{n\to{\infin}}\sqrt[n]{u_{n}} n→∞limnun= lim n → ∞ ∣ u n ∣ n \lim\limits_{n\to{\infin}}\sqrt[n]{|u_{n}|} n→∞limn∣un∣= ∣ x ∣ |x| ∣x∣,当 ∣ x ∣ < 1 |x|<1 ∣x∣<1时,级数收敛,所以收敛半径为 R = 1 R=1 R=1
- 方法2:
- 幂级数的系数为 a n a_{n} an= ( − 1 ) n − 1 n (-1)^{n-1}n (−1)n−1n, ∣ a n + 1 a n ∣ |\frac{a_{n+1}}{a_{n}}| ∣anan+1∣= n + 1 n \frac{n+1}{n} nn+1
- 从而 ρ \rho ρ= lim n → ∞ ∣ a n + 1 a n ∣ \lim\limits_{n\to{\infin}}|\frac{a_{n+1}}{a_{n}}| n→∞lim∣anan+1∣= 1 1 1,半径为 R = 1 ρ R=\frac{1}{\rho} R=ρ1=1
- 方法3:(最为方便)
- ∣ a n ∣ n \sqrt[n]{|a_n|} n∣an∣= n n \sqrt[n]{n} nn
- 从而 ρ \rho ρ= lim n → ∞ ∣ a n ∣ \lim\limits_{n\to{\infin}}\sqrt{|a_n|} n→∞lim∣an∣= lim n → ∞ n n \lim\limits_{n\to{\infin}}\sqrt[n]{n} n→∞limnn= 1 1 1
- 方法1:
- (2)求收敛域:
- x = − 1 x=-1 x=−1时,得常数项级数 ∑ n = 1 ∞ n \sum_{n=1}^{\infin}n ∑n=1∞n,显然发散
- x = 1 x=1 x=1,时,得常数项级数 ∑ n = 1 ∞ ( − 1 ) n − 1 n \sum_{n=1}^{\infin}(-1)^{n-1}n ∑n=1∞(−1)n−1n,此级数发散
- 事实上, x = ± 1 x=\pm{1} x=±1时,两个级数的一般项在 n → ∞ n\to{\infin} n→∞时不趋于0,所以发散
- 所以收敛域为 ( − 1 , 1 ) (-1,1) (−1,1)
- (3)确定和函数
- s ( x ) s(x) s(x)= ∑ n = 1 ∞ u n \sum_{n=1}^{\infin} u_{n} ∑n=1∞un, x ∈ ( − 1 , 1 ) x\in{(-1,1)} x∈(−1,1)
- 两边积分作 [ 0 , x ] [0,x] [0,x]区间上的积分: ∫ 0 x s ( t ) d t \int_{0}^{x}s(t)\mathrm{d}t ∫0xs(t)dt= ∑ n = 1 ∞ ∫ 0 x ( − 1 ) n − 1 n t n − 1 d t \sum_{n=1}^{\infin} \int_{0}^{x}(-1)^{n-1}nt^{n-1}\mathrm{d}t ∑n=1∞∫0x(−1)n−1ntn−1dt= ∑ n = 1 ∞ ( − 1 ) n − 1 x n \sum_{n=1}^{\infin}(-1)^{n-1}x^{n} ∑n=1∞(−1)n−1xn= x − x 2 + x 3 − ⋯ x-x^2+x^3-\cdots x−x2+x3−⋯
(1)- 考虑常用的已知级数 1 1 − x \frac{1}{1-x} 1−x1= 1 + x + x 2 + x 3 + ⋯ 1+x+x^2+x^3+\cdots 1+x+x2+x3+⋯
(2),有 1 1 − ( − x ) \frac{1}{1-(-x)} 1−(−x)1= 1 − x + x 2 − x 3 + ⋯ 1-x+x^2-x^3+\cdots 1−x+x2−x3+⋯= 1 1 + x \frac{1}{1+x} 1+x1(3) - 可知式(1)可以表示为 − ( 1 1 + x − 1 ) -(\frac{1}{1+x}-1) −(1+x1−1)= x 1 + x \frac{x}{1+x} 1+xx
- 因此 ∫ 0 x s ( t ) d x \int_{0}^{x}s(t)\mathrm{d}x ∫0xs(t)dx= x 1 + x \frac{x}{1+x} 1+xx,两边求导,得 s ( x ) s(x) s(x)= 1 + x − x ( x + 1 ) 2 \frac{1+x-x}{(x+1)^2} (x+1)21+x−x= 1 ( 1 + x ) 2 \frac{1}{(1+x)^2} (1+x)21, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 考虑常用的已知级数 1 1 − x \frac{1}{1-x} 1−x1= 1 + x + x 2 + x 3 + ⋯ 1+x+x^2+x^3+\cdots 1+x+x2+x3+⋯
相关文章:

AM@幂级数性质@幂级数和函数求解
文章目录 幂级数性质四则运算性质分析性质求解和函数例例 幂级数性质 和多项式有相似的性质本文介绍用幂级数的性质求解幂级数和函数的两个例子 四则运算性质 若幂级数 ∑ n 0 ∞ a n x n \sum_{n0}^{\infin}a_{n}x^{n} ∑n0∞anxn(1)的收敛半径为 R 1 R_1 R1,和函数为…...

PHP低版本安全问题
目录 1、PHP弱类型问题 1.1 MD5、 SHA1 弱比较问题 1.2 数组 0 1)函数无法处理数组,返回0 2)strcmp 2、特殊字符串导致的问题 2.1 "ffifdyop" 与 md5(string,raw) 2.2 ereg函数漏洞:00 截断 3、正则匹配问…...

结构体——C语言初阶
一.结构体的声明: (1)结构的基础知识: 结构体是一种构造数据类型把不同类型的数据组合成一个整体结构体是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量需要注意的是,结构体是一种…...

基于django电影推荐系统
基于django电影推荐系统 摘要 该Django电影推荐系统是一个简单而基础的框架,旨在展示系统的基本组件。系统包括两个主要模型,即Movie和Rating,用于存储电影信息和用户评分。视图层包括展示电影列表和电影详情的功能,使用模板进行页…...
【问题处理】WPS提示不能启动此对象的源应用程序如何处理?
哈喽,大家好,我是雷工! 最近在用WPS打开word文件中,插入的Excel附件时,无法打开,提示:“不能启动此对象的源应用程序”。 经过上网查找处理办法,尝试解决,现将解决过程记…...
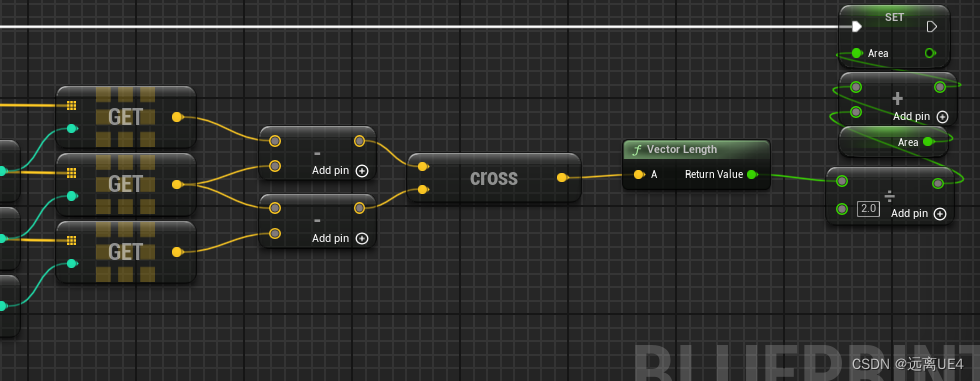
UE 程序化网格 计算横截面
首先在构造函数内加上程序化网格,然后复制网格体到程序化网格组件上,将Static Mesh(类型StaticMeshActor)的静态网格体组件给到程序化网格体上 然后把StaticMesh(类型为StaticMeshActor)Instance暴漏出去 …...

【Spring】IoC容器的一些总结与补充
文章目录 1. 创建容器的两种方式相对路径导入绝对路径导入 2. 获取Bean的三种方式getBean后强转类型getBean内写明类别根据类别获取bean 3. 容器层次结构4. BeanFactory5. bean的总结6. 注入的总结 1. 创建容器的两种方式 相对路径导入 ApplicationContext ctx new ClassPat…...

Java GUI实现五子棋游戏
五子棋是一种双人对弈的棋类游戏,通常在棋盘上进行。棋盘为 1515 的方格,黑白双方各执棋子,轮流在棋盘的格点上落子,先在横、竖、斜线上形成五个相连的同色棋子者获胜。五子棋规则简单,易学难精,兼具攻防和…...

Python 集成 Nacos 配置中心
Python 集成 Nacos 配置中心 下载 Nacos 官方 pyhton 库 pip install nacos-sdk-python # 指定国内阿里云镜像源 pip3 install nacos-sdk-python -i http://mirrors.aliyun.com/pypi/simple/ --trusted-host mirrors.aliyun.com配置 Nacos 相关信息 Global:nacos:port: 8848…...

Debian 11 更新 Node.js 版本
发布于 2023-07-14 在 https://chenhaotian.top/debian/d-upd-nodejs/ 步骤 从 NodeSource 服务下载需要的 Node.js 安装脚本。注意更换版本号。当前的 LTS 版本是 18.x curl -sL https://deb.nodesource.com/setup_18.x | sudo -E bash -现在可以直接从 apt 安装࿰…...

python 对图像进行聚类分析
import cv2 import numpy as np from sklearn.cluster import KMeans import time# 中文路径读取 def cv_imread(filePath, cv2_falgcv2.COLOR_BGR2RGB): cv_img cv2.imdecode(np.fromfile(filePath, dtypenp.uint8), cv2_falg) return cv_img# 自定义装饰器计算时间 def…...

程序员导航站
探路者 hello.alluniverse.vip 开发者导航 - Pro Developer网站导航 探路者是一款极简导航工具,致力于收录的每个站点都有其独特的作用。同时支持自定义导航,让用户快速实现个性化的导航站点。 特性概述 免费ChatGPT 装机必备 开发工具 Git精选项目 …...

BIO、NIO、AIO三者的区别及其应用场景(结合生活例子,简单易懂)
再解释三者之前我们需要先了解几个概念: 阻塞、非阻塞:是相较于线程来说的,如果是阻塞则线程无法往下执行,不阻塞,则线程可以继续往下 执行。同步、异步:是相较于IO来说的,同步需要等待IO操作完…...
深度学习YOLO图像视频足球和人体检测 - python opencv 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果3 卷积神经网络4 Yolov5算法5 数据集6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习YOLO图像视频足球和人体检测 该项目较为新颖,适合作为竞赛课题方向,学长非…...
系列七、JVM的内存结构【堆(Heap)】
一、概述 一个JVM实例只存在一个堆内存,堆内存的大小是可以手动调节的。类加载器读取了类文件后,需要把类、方法、常变量放到堆内存中,保存所有引用类型的真实信息,以方便执行器执行,堆内存分为三个部分,即…...
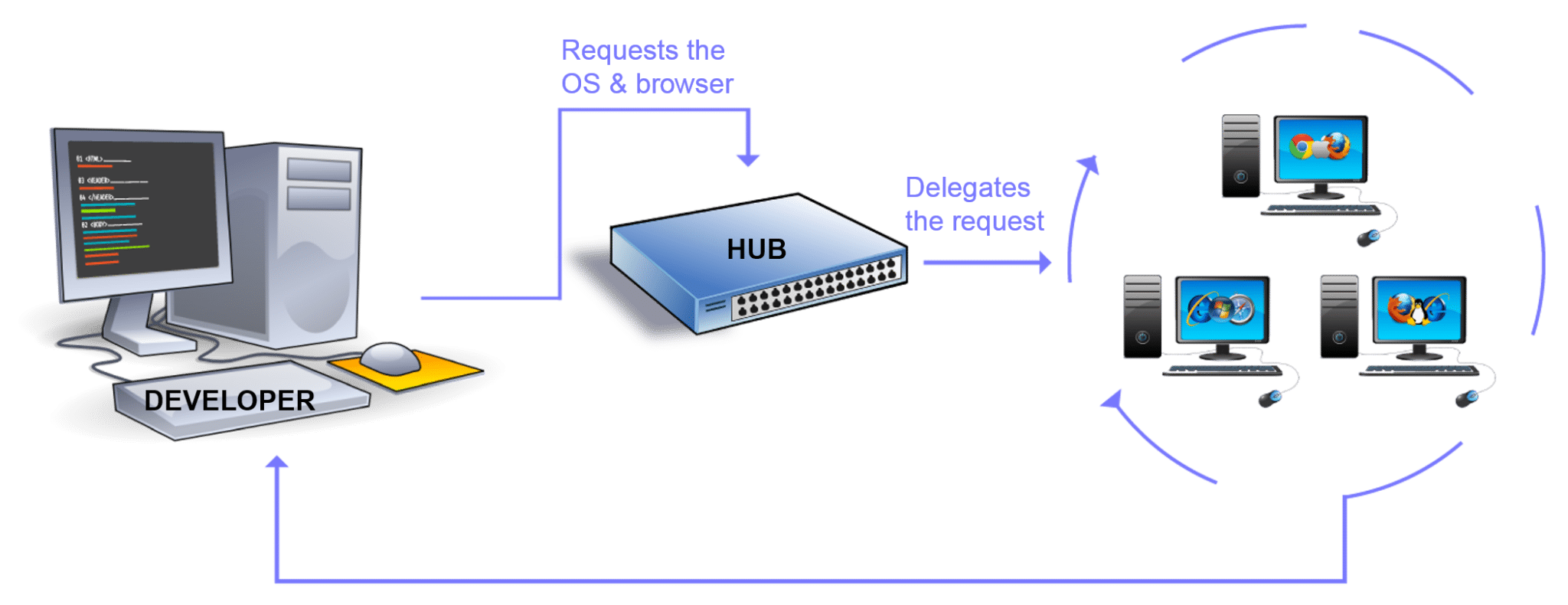
什么是Selenium?如何使用Selenium进行自动化测试?
什么是 Selenium? Selenium 是一种开源工具,用于在 Web 浏览器上执行自动化测试(使用任何 Web 浏览器进行 Web 应用程序测试)。 等等,先别激动,让我再次重申一下,Selenium 仅可以测试Web应用…...

【蓝桥杯 第十五届模拟赛 Java B组】训练题(A - I)
目录 A、求全是字母的最小十六进制数 B、Excel表格组合 C、求满足条件的日期 D、 取数字 - 二分 (1)暴力 (2)二分 E、最大连通块 - bfs F、哪一天? G、信号覆盖 - bfs (1)bfs…...

【数据结构】手撕双向链表
目录 前言 1. 双向链表 带头双向循环链表的结构 2. 链表的实现 2.1 初始化 2.2 尾插 2.3 尾删 2.4 头插 2.5 头删 2.6 在pos位置之前插入 2.7 删除pos位置 3.双向链表完整源码 List.h List.c 前言 在上一期中我们介绍了单链表,也做了一些练习题&…...
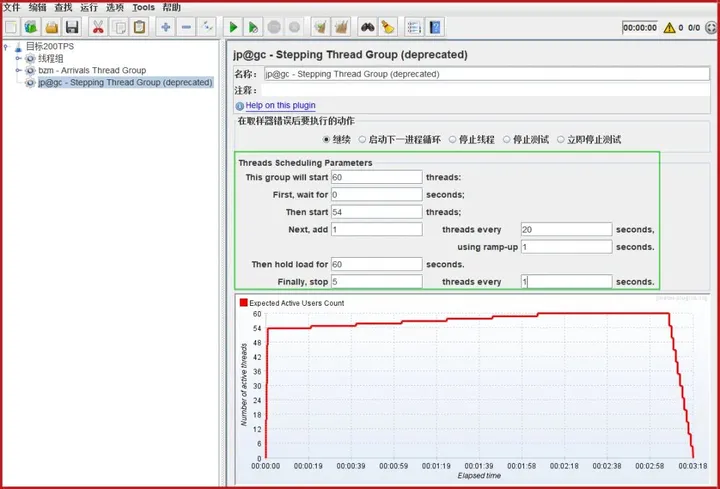
性能测试 —— Jmeter接口处理不低于200次/秒-场景
需求:期望某个接口系统的处理能力不低于200次/秒,如何设计? ①这个场景是看服务器对某个接口的TPS值是否能大于等于200,就可以了; ②系统处理能力:说的就是我们性能测试中的TPS; ③只要设计一…...

Qt中使用QNetworkAccessManager类发送https请求时状态码返回0
前言 在项目开发中,碰到一个问题,使用QNetworkAccessManager类对象发送https请求时,状态码一直返回0,抓包分析看请求响应也是正常的。费了好大劲终于搞定了,主要是两个原因导致的。 原因一:未设置支持SSL…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
