HashMap原理(一):哈希函数的设计
目录导航
- 哈希函数的作用与本质
- 哈希函数设计
- 哈希表初始容量的校正
- 哈希表容量为2的整数次幂的缺陷及解决办法
注:为了简化代码,提高语义,本文将HashMap很多核心代码抽出并根据代码含义为代码片段取名,完全是为了方便读者理解。
哈希函数的作用与本质
HashMap用来存储具有映射关系的数据对{key, value},在内部通过构造复合数据结构来封装数据对,即
//伪代码,非源码
class Pair<K, V> {public K key;public V value;
}
假设用来存储数据对的哈希数表为table,数据对Pair的存储位置通过计算key得到,key => index,则Pair将存储在table[index]处。
哈希函数就是用来计算哈希索引的工具。fun(key,table) = index, 0 <= index < table.length
入参key为整数,若key不为整数,则需要先将key转化为整数再参与计算。在Java中,每个对象都有一个public int hashCode();方法,起的就是这样的转化作用。
哈希函数设计
构造哈希函数最常见的策略是取余法,即index = int_key % table.length。
HashMap也是采用取余法构造哈希函数,并强制哈希表的容量table.length为2的整数次幂,即2^n,这样便可采用位运算计算余数以提高运算效率:(table.length - 1) & key.hashCode()。
因为当table.length = 2^n时,其二进制形式只有第(n + 1)位为1,其余皆为0。任何一个整数对table.length求余,实际上就是取这个整数的低n位的值。
例如table.length = 16 = 2^4,直接通过模运算将得到18 % 16 = 2。

而table.length - 1 = 2^n -1,其二进制形式低n位均为1,其余比特位皆为0。
以table.length = 16 = 2 ^ 4为例,table.length - 1 = 15,即
0000 0000 0000 0000 0000 0000 0000 1111,低4位均为1,其余比特位皆为0
table.length - 1恰好是对任意一个整数低n位的遮罩, 当用这个遮罩与任意一个整数进行位与操作时,恰好得到这个整数对table.length求余的余数。
那么18 & (16 -1) = 18 % 16 = 2,

哈希表初始容量的校正
创建HashMap时,允许指定哈希表的初始容量,即table.length。HashMap没有强制要求使用者传入的初始容量为2的整数次幂,而是在内部自动转化。若使用者传入的初始容量为capacity,那么转化后的哈希表容量为大于等于capacity的最小的一个2的整数次幂。如,9~15都会转为为16 = 2^4,17~31都会转成2^5 = 32,以此类推。
从二进制的角度看,使用者传入的初始容量为capacity(先不考虑capacity恰好是2的整数次幂的情况),如果它比特值为1的最高位处在第k位,那么转化后的值就是2^k。
以129 = 2 ^7 + 1为例,
比特值为1的最高位处在第8位,那么转化后的值便是2^8 = 256。

HashMap采用的策略是,如果初始容量capacity的比特值为1的最高位处在第k位,那么将低(k - 1)位全部置为1,再把结果值 + 1,恰好得到转换后的目标容量。以129 = 2 ^7 + 1为例,比特值为1的最高位处在第8位,那么将低7位全部置为1得到255,255再加1等于256。

具体计算方法上,将capacity不断进行无符号右移再与原值进行位或操作,我们还是通过capacity = 129,k = 8来一步步说明。
第一步,将129无符号右移一位,得到结果64,结果的第k-1位必定为1。

然后将129与64做位或操作得到结果193,由于位或操作中,两个比特为只要有一个为1,那么结果必为1,如此,确保了最终结果第k - 1位变为1。

第二步,经过第一步,第k位,k - 1位都为1,所以我们可以把193无符号右移2位,得到结果48,结果的第k-2位及第k-3位必定为1。

然后将193与48做位或操作,得到结果241,最终结果第k位到第(k - 3)位,总共四位都变为1。

第三步,经过前面的操作,得到的结果241的第k位到(k-3)位,总共四位均变为1,所以将241无符号右移4位,得到结果15,其低4位均为1。

再将241与15进行位或操作,得到结果255,至此目标结果的低8位全部置为1。

因为用户传入的初始容量capacity,其比特值为1的最高位可能是第31位,所以为了囊括所有的可能,会继续无符号右移,直至移够31位,每次移动的位数恰好是上一次的2倍。
对于上面的例子,接下来要无符号右移8位。将255 无符号右移8位得到0。

将255与0进行位或,结果不变还是255。

接下来,位移16位,结果为0,再与255位或,结果还是255。至此已经总共无符号右移了(1 + 2 + 4 + 8 + 16) = 31位,位移结束。
最后,255 + 1 = 256。

按照上面的算法,哈希表初始容量的校正代码如下:
int adjustCapacity(int cap) {int n = cap;n |= n >>> 1;n |= n >>> 2;n |= n >>> 4;n |= n >>> 8;n |= n >>> 16;return n}
我们还有遗留的一个问题没有讨论,假如使用者传入的初始容量capacity本来就是2的整数次幂,如capacity = 128 = 2^(k - 1),k = 8,那么将低(k - 1) = 7位全部置为1,将得到255。这是完全没必要的,因为我们可以直接采用128。

那么,如果想把这样的capacity也统一到我们的计算公式里,我们只需要在开始位移前,将初始容量减1,然后再开始位移。比如capacity = 128,c - 1 = 127,127的二进制表示法中,比特值为1的最高位处在第7位,将其低6位全部置为1,结果还是127,然后加1得到目标结果128。

对于初始容量capacity不是2的整数次幂的情况,将capacity - 1再通过adjustCapacity计算,结果跟直接通过capacity计算的结果一致。
最后再考虑下边界值问题。
当capacity = 0,直接取1 = 2^0,
在java中,一个int值能表示的最大的2的整数次幂是2^(k -1),k = 31,即2^30,所以当capacity的二进制形式中,比特值为1最
高位处在第31位时,那么位移结束后目标结果将是2^32 - 1,
即除了符号位全是1,此时再加1将产生溢出,所以直接取2^30。
最终的adjustCapacity如下:
int tableSizeFor(int cap) {int n = cap - 1;n |= n >>> 1;n |= n >>> 2;n |= n >>> 4;n |= n >>> 8;n |= n >>> 16;return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;}
哈希表容量为2的整数次幂的缺陷及解决办法
当哈希表容量为2的整数次幂时,即capacity = 2^m,那么任何整数对其求余,等同于取该整数二进制表示形式的低m位的值。
比如capacity = 16 = 2^4。
key = 65538时,65538 & (16 -1) = 2,也就是取65538的低4位的值。

key = 2时,2 & (16 -1) = 2,取低4位的值还是2。

通过这个例子我们可以发现,当哈希表容量为2的整数次幂时,即capacity = 2^m,只要key的低m位的值相同,他们通过求余法计算的哈希索引就相等,即产生了哈希冲突。
为了降低产生哈希冲突的概率,我们需要利用剩余比特位的值。
首先将key无符号右移16位,得到一个结果,这个结果的高16位为0,低16位为原先的高16的值,以65538为例,

接着将位移后的结果与key的原值进行位异或操作,由于比特值0与任何比特值位异或得到都是后者本身,比热值1与任何比热值位异或得到都是后者取反后的值。那么原高16位中值为1的比特位就会改变低16位中对应位置的比特值。

再将这个结果作为新的key代入哈希函数计算,65539 & (16 - 1) = 3。

当key = 2,2无符号右移16位,得到0。

2跟0进行位异或还是2。

最后将2作为最终结果代入哈希函数计算,得到结果0。
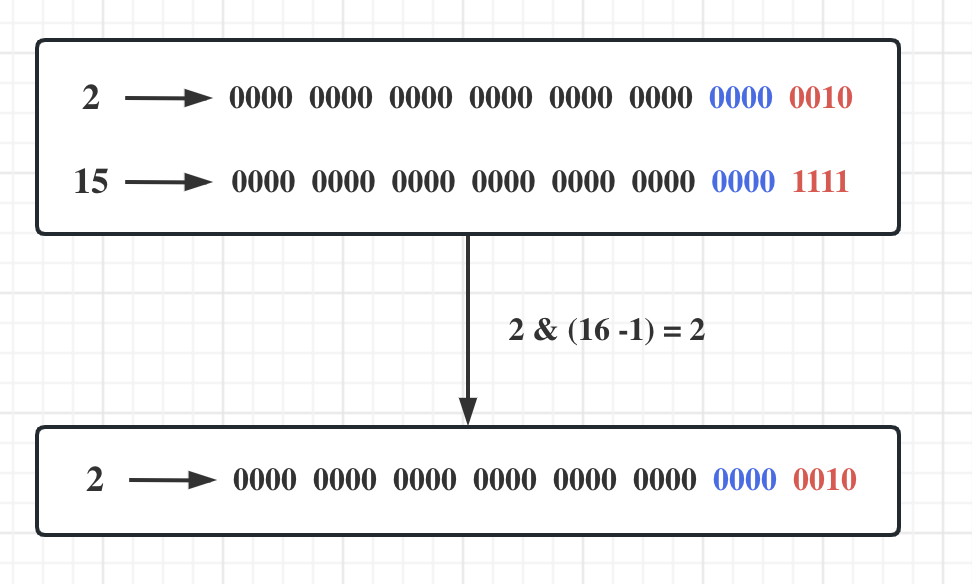
通过这样的操作,虽然2和65538的低4位相同,但得出的哈希索引却不同,从而降低了哈希碰撞的概率。
最终的哈希函数变为:
//先对key进行转化,降低哈希碰撞的概率int transformKey(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);}int hash(int key){//table.length为2的整数次幂,所以可通过位运算取代模运算,提高运算效率return (table.length - 1) & key;}
相关文章:

HashMap原理(一):哈希函数的设计
目录导航哈希函数的作用与本质哈希函数设计哈希表初始容量的校正哈希表容量为2的整数次幂的缺陷及解决办法注:为了简化代码,提高语义,本文将HashMap很多核心代码抽出并根据代码含义为代码片段取名,完全是为了方便读者理解。哈希函…...
06--WXS 脚本
1、简介WXS(WeiXin Script)是小程序的一套脚本语言,结合 WXML ,可以构建出页面的结构。 注意事项WXS 不依赖于运行时的基础库版本,可以在所有版本的小程序中运行。WXS 与 JavaScript 是不同的语言,有自己的…...
【Vue3】vue3 + ts 封装城市选择组件
城市选择-基本功能 能够封装城市选择组件,并且完成基础的显示隐藏的交互功能 (1)封装通用组件src/components/city/index.vue <script lang"ts" setup name"City"></script> <template><div class…...
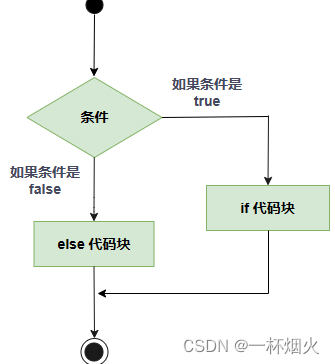
C语言if判断语句的三种用法
C if 语句 一个 if 语句 由一个布尔表达式后跟一个或多个语句组成。 语法 C 语言中 if 语句的语法: if(boolean_expression) {/* 如果布尔表达式为真将执行的语句 */ }如果布尔表达式为 true,则 if 语句内的代码块将被执行。如果布尔表达式为 false&…...

React中echarts的封装
做大屏的时候经常会遇到 echarts 展示 在 React (^18.2.0) 中对 echarts (^5.4.0) 的简单封装 echarts 封装使用 props 说明 参数说明类型可选值默认值opts初始化传入的 opts https://echarts.apache.org/zh/api.html#echarts…...

IV测试系统3A太阳能模拟器在光伏中应用
一、概述IV测试系统3A太阳能模拟器应具备光束准直、光斑均匀、辐照稳定、且与太阳光谱匹配的特点,使用户可足不出户的完成需要太阳光照条件的测试。科迎法电气提供多规格高品质的太阳模拟器,可适用于单晶硅、多晶硅、非晶硅、染料敏化、有机、钙钛矿等各…...
Vue 中过滤器 filter 使用教程
Vue 过滤器 filter 使用教程文章目录Vue 过滤器 filter 使用教程一、过滤器1.1 过滤器使用的背景1.2 格式化时间的不同实现1.3 过滤器的使用1.4 过滤器总结一、过滤器 1.1 过滤器使用的背景 过滤器提供给我们的一种数据处理方式。过滤器功能不是必须要使用的,因为它…...
源码numpy笔记
参考文章 numpy学习 numpy中的浅复制和深复制的详细用法 numpy中的np.where torch.gather() Numpy的核心数据结构,就叫做array就是数组,array对象可以是一维数组,也可以是多维数组 array本身的属性 shape:返回一个元组…...
【VUE】六 路由和传值
目录 一、 路由和传值 二、案例 三、案例存在无法刷新问题 一、 路由和传值 当某个组件可以根据某些参数值的不同,展示不同效果时,需要用到动态路由。 例如:访问网站看到课程列表,点击某个课程,就可以跳转到课程详…...

ChatGPT修炼指南和它的电力畅想
近期,ChatGPT刷屏各大社交平台,无疑成为人工智能界最靓的仔! 身为一款“会说话”的聊天机器人程序,它与前辈产品Siri、小度、微软小冰等有什么不同?先来听听小伙伴们怎么说。 ChatGPT何以修炼得这么强大?…...
基于vscode开发vue项目的详细步骤教程
1、Vue下载安装步骤的详细教程(亲测有效) 1_水w的博客-CSDN博客 2、Vue下载安装步骤的详细教程(亲测有效) 2 安装与创建默认项目_水w的博客-CSDN博客 目录 五、vscode集成npm开发vue项目 1、vscode安装所需要的插件: 2、搭建一个vue小页面(入门vue) 3、大致理解…...
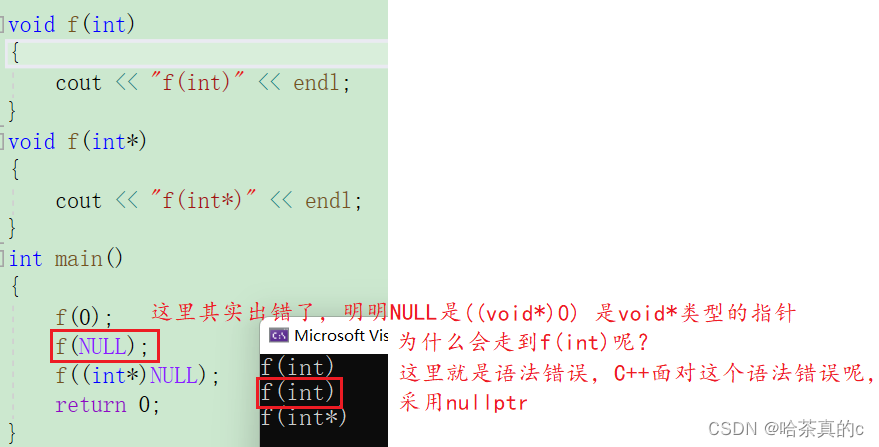
【C++初阶】1. C++入门
1. 前言 1. 什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机, 20世纪80年代, 计算机界提出了OOP(…...
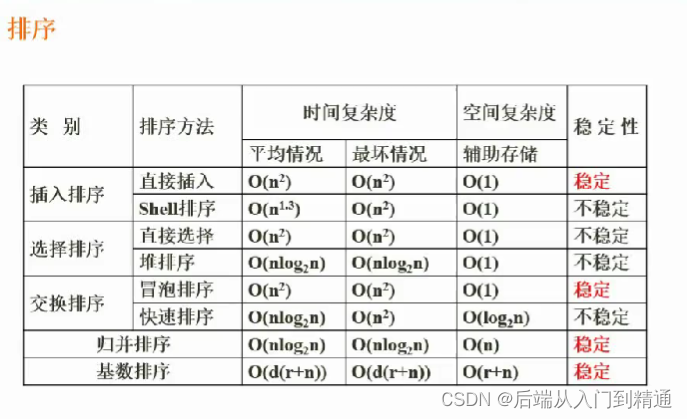
数据结构与算法(二十)快速排序、堆排序(四)
数据结构与算法(三)软件设计(十九)https://blog.csdn.net/ke1ying/article/details/129252205 排序 分为 稳定排序 和 不稳定排序 内排序 和 外排序 内排序指在内存里,外排序指在外部存储空间排序 1、排序的方法分类。 插入排序ÿ…...
)
TensorRT量化工具pytorch_quantization代码解析(二)
有些地方看的不是透彻,后续继续补充! 继续看张量量化函数,代码位于:tools\pytorch-quantization\pytorch_quantization\tensor_quant.py ScaledQuantDescriptor 量化的支持描述符:描述张量应该如何量化。QuantDescriptor和张量…...

buu [BJDCTF2020]easyrsa 1
题目描述 : from Crypto.Util.number import getPrime,bytes_to_long from sympy import Derivative from fractions import Fraction from secret import flagpgetPrime(1024) qgetPrime(1024) e65537 np*q zFraction(1,Derivative(arctan(p),p))-Fraction(1,Deri…...

taobao.user.openuid.getbyorder( 根据订单获取买家openuid )
¥免费不需用户授权 根据订单获取买家openuid,最大查询30个 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 请求示例 TaobaoClient client new DefaultTaobaoClient(url, appkey, secret); UserOpenuidGetbyorderR…...
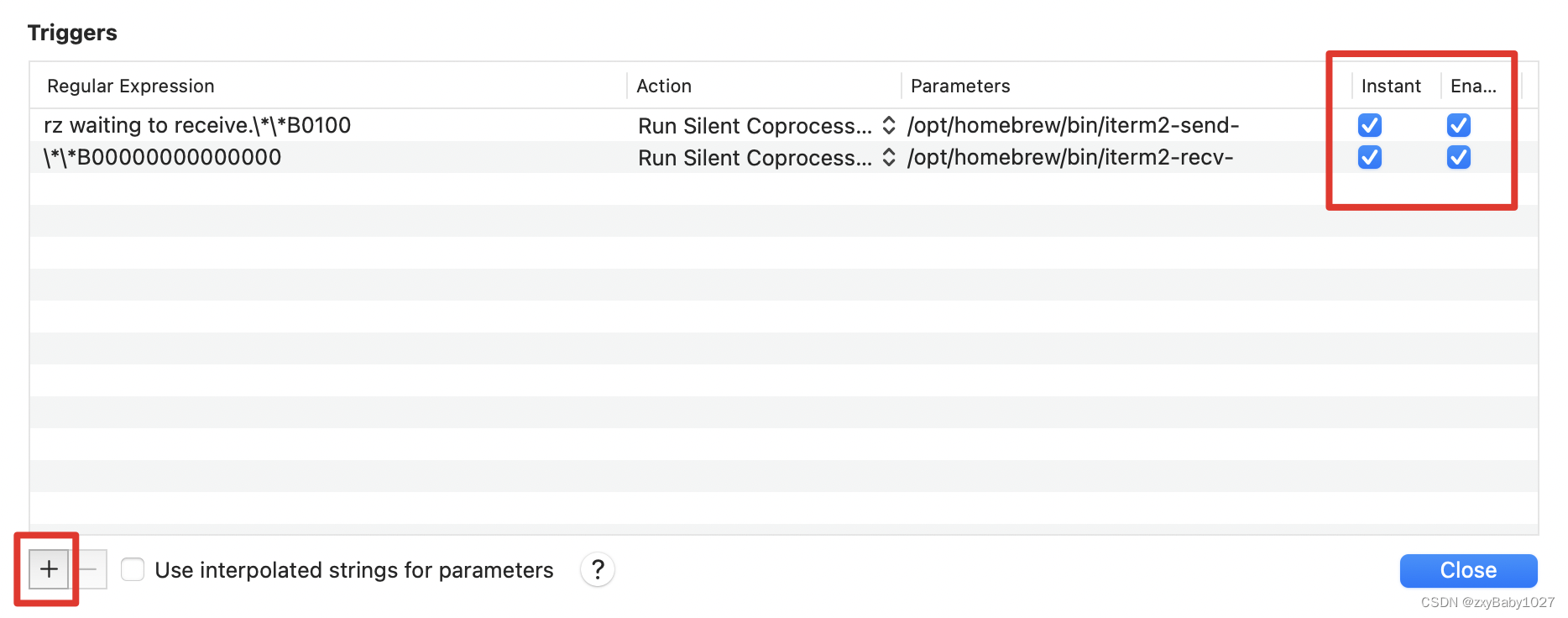
Mac iTerm2 rz sz
1、安装brew(找了很多🔗,就这个博主的好用) Mac如何安装brew?_行走的码农00的博客-CSDN博客_mac brew 2、安装lrzsz brew install lrzsz 检查是否安装成功 brew list 定位lrzsz的安装目录 brew list lrzsz 执…...
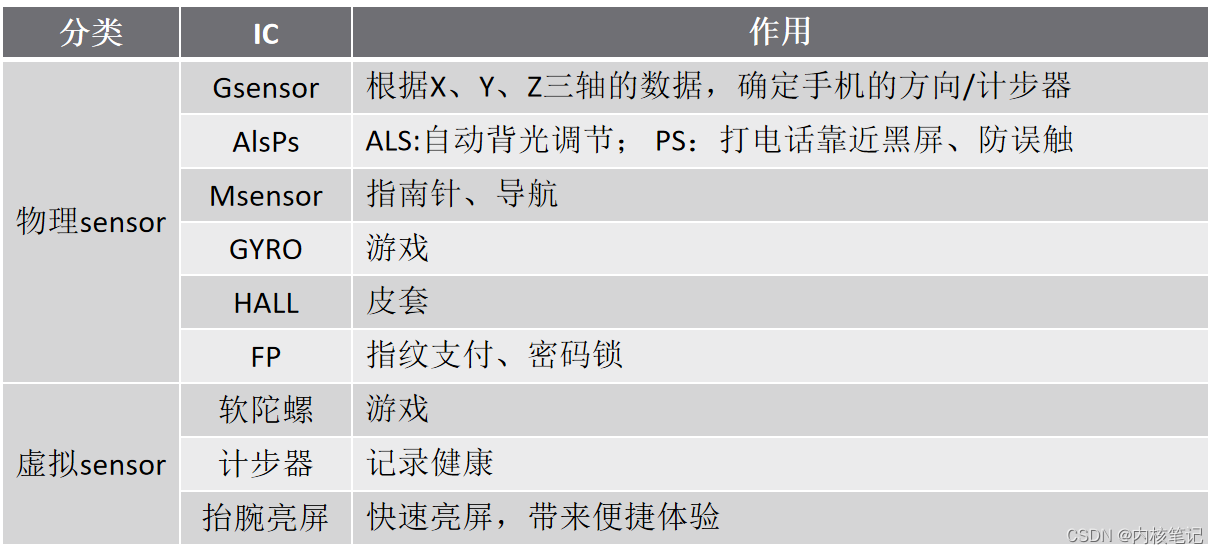
高通平台开发系列讲解(Sensor篇)Gsensor基础知识
文章目录 一、什么是SENSOR?二、Sensor的分类及作用三、Gsensor的工作原理及介绍3.1、常见Gsensor3.2、Gsensor的特性沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍 Sensor 基础 一、什么是SENSOR? 传感器(英文名称:sensor )是一种检测装置,能感…...

图像处理实战--Opencv实现人像迁移
前言: Hello大家好,我是Dream。 今天来学习一下如何使用Opencv实现人像迁移,欢迎大家一起参与探讨交流~ 本文目录:一、实验要求二、实验环境三、实验原理及操作1.照片准备2.图像增强3.实现美颜功能4.背景虚化5.图像二值化处理6.人…...
OnlyOffice验证(二)在Centos7上部署OnlyOffice编译结果
在Centos7上部署OnlyOffice编译结果 此处将尝试将OnlyOffice验证(一)DocumentServer编译验证的结果部署到Centos7上。并且使用其它服务器现有的RabbitMq和Mysql。 安装Nginx 先安装Nginx需要的依赖环境: yum install openssl* -y yum insta…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
